采用DDPG的联合波束成形和功率控制算法

李中捷，高 伟，熊吉源，李江虹

(1.中南民族大学 电子信息工程学院，湖北 武汉 430074；2.中南民族大学 智能无线通信湖北重点实验室，湖北 武汉 430074)

大数据、物联网和人工智能的发展，对移动通信的传输速率、信道容量等要求日渐提升。未来十年之内，移动数据需求量预计会增加上千倍。为满足需求，主流的电信公司以及全球标准化组织都在积极推动第五代无线通信(5th-Generation，5G)的研发。毫米波通信比传统的微波通信具有更高的频段，但毫米波通信具有路径损耗高的问题。目前，采用大规模天线阵列以构建多输入多输出(Multiple-Input Multiple-Output，MIMO)通信系统，并结合波束成形技术来增强接收端的信噪比，可有效弥补毫米波通信路径损耗高的问题。因此，毫米波和大规模多输入多输出技术结合被认为是5G通信的前景技术之一。大量未利用的毫米波频谱资源以及与波束成形技术的结合，可显著提高通信系统的性能。

毫米波通信采用波束成形技术来弥补路径损耗而造成的链路预算差距[1-4]。文献[1]研究了在固定波束模式下的功率控制问题，致力于在保证最小用户速率的情况下最大化总速率。文献[2]通过固定发射功率的随机波束成形来分析毫米波通信的性能。文献[3]采用大数据分析技术，在高速移动的通信环境下借助用户的位置信息，提出了两种波束成形设计方案来获得较高的频谱效率，表明最佳传输策略的设计与用户位置之间的映射关系十分重要。

目前已有一些工作专注于功率控制以提高通信中的频谱效率[5-8]，例如分式规划算法[5]和加权最小均方误差算法[6]。上述算法均根据完整信道状态信息构建精确的数学模型，并通过迭代的方式进行计算。因此两种算法会造成大量的计算消耗，且现实中完整的信道状态信息并不易于获取。为解决上述问题，文献[7]提出了基于深度Q网络(Deep Q Network，DQN)的功率控制算法，将深度Q网络应用于发射功率控制问题，提出了基于深度Q网络的动态功率控制方案。深度Q网络只适用于离散的动作空间，发射功率必须进行量化。将发射功率进行量化成若干个等级，然后使用深度Q网络进行等级选取。因此量化器的设计和功率级别数量的设定都会对性能产生影响。

上述研究仅考虑了通信中的波束成形设计或功率控制问题，从而导致传输速率的损失。为进一步提高数据传输速率，已有大量工作针对联合功率控制和波束成形问题进行研究[9-11]。文献[9]研究了在毫米波多用户场景下联合功率控制和波束成形问题，对具有恒模约束的波束成形矩阵进行设计。文献[11]研究了在高速移动时通信的联合混合波束形成和功率控制设计问题。然而上述文献对波束成形矩阵进行设计时均需要完整的信道状态信息。

针对上述问题，笔者提出了基于强化学习的联合波束成形和功率控制算法，在无需完整信道状态信息的情况下，对联合波束成形和功率控制问题进行求解。联合波束成形和功率控制问题是非凸的，因此将原始问题分为波束成形设计和功率控制两个子问题，并提出了基于强化学习的双模型系统进行求解。模型采用集中式训练分布式执行结构。首先设计信息交互协议助于基站了解环境信息，每个基站与环境交互后将经验上传至云端进行训练。云端采用深度Q网络对波束成形矩阵进行设计。深度Q网络只适用于离散的动作空间，而发射功率为连续变量，故采用深度确定性策略梯度(Deep Deterministic Policy Gradient，DDPG)[12]算法来代替深度Q网络对功率控制问题进行求解，最后云端将训练完成的网络权重广播给每一个基站。

1 系统模型

如图1所示，笔者采用K个单元组成的蜂窝网络，其中每个小区中均含有一个多天线发射基站(Base Stalion，BS)和M个单天线接收用户(User Equipnent，UE)。所有基站配备N(N≥1)根天线的均匀线性线阵。t时刻小区k中UEm接收的信号可表示为

(1)

(2)

(3)

基于毫米波频率的稀疏散射特性，采用几何信道模型来捕获毫米波信道的特性。t时刻，BSk和UEm之间的信道向量可表示为

(4)

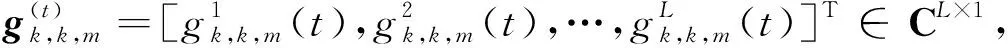
A(N，θk，k，m，Δ)=[a1(N，φ1)，a2(N，φ2)，…，aL(N，φL)]∈CN×L，

(5)

其中，θk，k，m为BSk和UEm的下行信道的发射角(Direction of Departure，DoD)；Δ指代一个小的角度范围，称为角扩展[14]；al(N，φl)∈CN×1，∀l∈{1，2，…，L}，表示第l条路径的阵列响应向量，可表示为

(6)

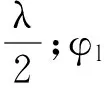
(7)

(8)

2 问题提出

笔者的目的是联合优化基站处的波束成形矢量和发射功率以最大化频谱效率，将联合波束成形和功率控制的优化问题表述为

(9)

其中，C1表示每个基站的发射功率在0和Pmax之间；C2表示每个基站的波束成形向量将在码本F中选出；C3表示最小速率约束，即要求每个通信链路的SINR将不能低于最低标准γmin。前两个约束的非凸性使得该问题是一个非凸优化问题，因此直接对式(9)进行求解十分困难。将求解式(9)分为两个子问题，首先对波束成形矩阵F(t)进行设计，然后对功率控制问题进行求解。

3 基于深度强化学习的联合功率控制和波束成形算法

3.1 信息交换议定

深度强化学习中基站通过与环境交互采取行动并获得奖励[16]，故设计信息交换议定使基站有效获取环境信息。

如图2所示，BSk与UEk进行通信时，周边的BS分为两个集合：干扰者和受干扰者。干扰者定义为：BSi的通信使BSk在通信时受到干扰，当BSk收到干扰信号的SINR大于一定阈值，基站i被定义为干扰者，可表示为

(10)

与此相似，当BSk通信时也会对周边BSo的通信产生干扰。故受干扰者定义为：BSk在通信时对BSo的通信产生干扰，且BSo收到干扰信号SINR大于一定阈值，BSo被定义为受干扰者，可表示为

(11)

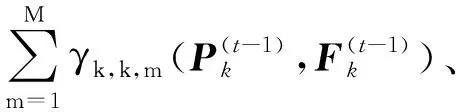
3.2 联合功率和波束算法

笔者提出的模型如图3所示，采用集中式训练分布式执行的结构。模型分为顶层和底层两部分。顶层设定波束向量，底层设定发射功率。接下来介绍方案的3个主要部分。

(1) 动作空间。动作集分为波束选择和功率选择两个动作空间。波束向量通过选取码本中最佳的波束向量索引进行设计，故顶层动作集由波束向量索引构成。采用文献[17]所提出的方案进行码本设计，表示为C=[c0，c1，…，cQcode-1]∈CN×Qcode。码本C的列表示波束方向，第n行q列的元素C[n，q]表示波束在方向第n根天线在方向q上的相位，可表示为

(12)

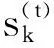
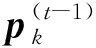
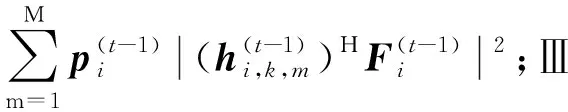
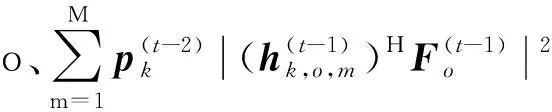
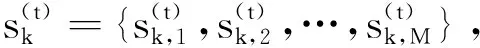
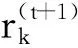
(13)

其中，第1项表示BSk在t时刻的频谱效率；第2项表示惩罚项，即对周边通信链路的干扰。换句话说，奖励函数可以被认为是动作对式(9)中目标函数影响的净增益。BSk的惩罚定义为受BSk干扰的受干扰者o的频谱效率损耗之和，即

(14)

每个基站视为一个代理，并视其周边基站为环境的一部分，使每个代理视为独立的个体。避免环境变化造成的影响，将所有代理的经验收集发送至云端并训练网络，然后将网络权重广播给所有代理。流程分为执行和训练两个步骤：

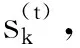
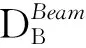
(15)

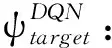
(16)

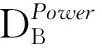
(17)

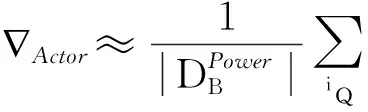
(18)

其中，θ表示网络权重。每隔Tu次训练将Critic和Actor网络权重覆盖目标Critic和目标Actor网络的网络权重：

(19)

(20)

算法伪代码如算法1所示。

算法1基于强化学习的联合波束成形和功率控制算法。

① 初始化模型参数。

② 基站k与环境交互获取经验eBeam和ePower，并上传至云端。

③ 开始迭代：

⑥ 采用式(15)对评估网络权重进行更新；

⑦ DDPG：

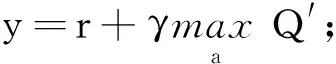
⑨ 采用式(17)、式(18)分别更新Critic和Actor网络权重；

4 仿真分析

4.1 参数设置

通过计算机仿真分析了算法的平均频谱效率，即总频谱效率除以通信链路的数目。文中采用了5个六角形的均匀蜂窝网络，每个蜂窝中心处放置基站，用户随机分布在网络内部。如图4所示，圆点表示UE，三角表示基站。系统详细参数如表1所示。此外，设定以基站为中心，半径r=10 m的小区域不放置用户。将路径损耗设为128.1+37.6 lgd，式中d表示发送端到接收端的直接距离。与文献[18]相似，计算频谱效率(3)时将其上限设为30 dB。

DDPG和DQN中采用的参数如表1和表2所示。

使用相对较小的网络进行训练，防止模型复杂化后导致计算时间较长。文献[19]表明，单层隐藏层的神经网络足以表征任何函数，然而该层的神经元必须足够大。巨大的单层网络无法更新权重至最优，采用3层隐藏层的神经网络训练效果更好。故算法中所有的神经网络均采用4层网络：输入层、输出层和两层隐藏层。输入层的神经元个数与代理的状态集中元素个数相等。采用ε贪心算法，探索值ε初始化为ε(0)=0.2，并随着迭代次数逐渐减小，ε(t+1)=max{εmin，(1-λε)ε(t)}，λε=10-4。

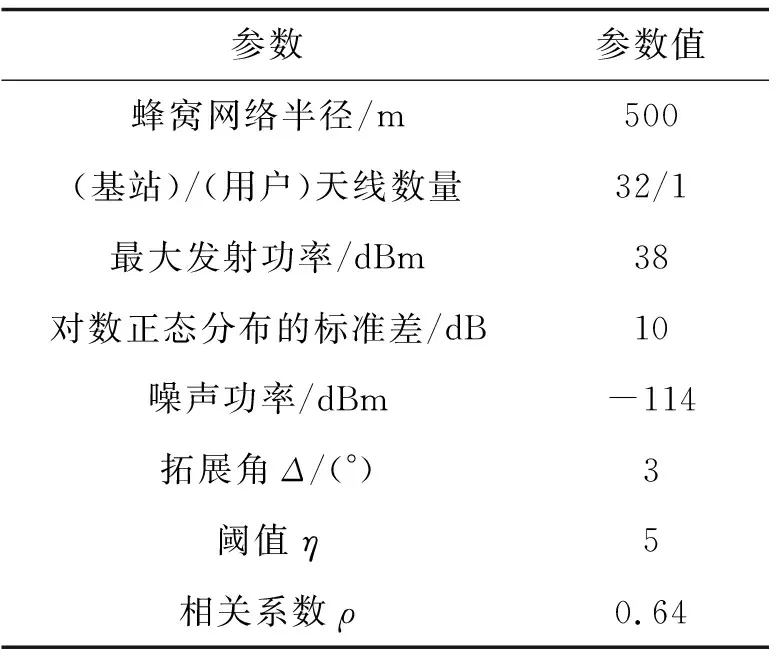
表1 系统参数

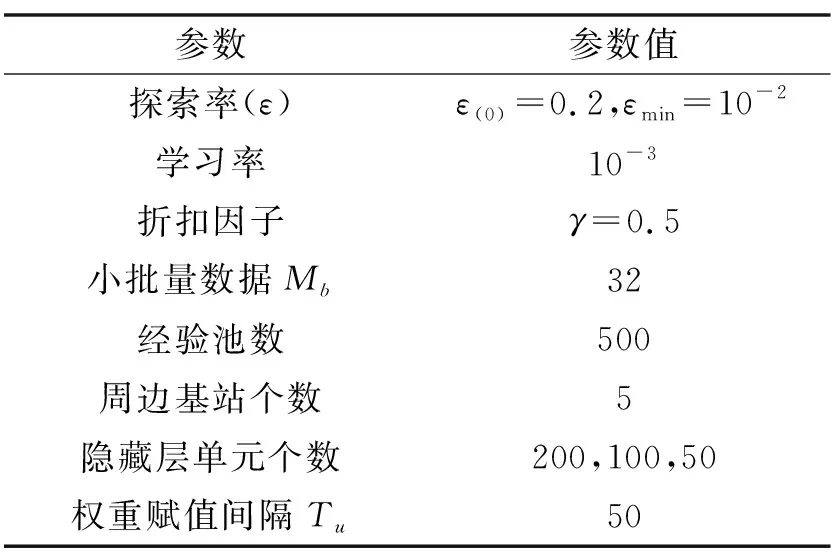
表2 模型参数

4.2 性能分析

在多用户mmWave通信场景下，与以下3种算法进行性能对比与分析。

基线1算法：基线算法文献[12]提出的基于深度Q网络的联合波束成形和功率控制算法。

基线2算法：BS的发射功率均设为最大时文献[4]提出的基于SVD分解波束成形算法。

基线3算法：基站的发射功率随时选取，基于SVD的波束成形算法BS的发射功率均设为最大时文献[4]提出的。

图5为毫米波通信环境中每个小区内用户数量为1时各算法的频谱效率性能。从图中可以看出，大约在训练3 500次后，笔者所提的基于深度学习的联合波束成形和功率控制算法收敛且取得最优的频谱效率。深度Q网络输出功率为量化的离散值使精度受到限制，故性能低于笔者所提算法。基站的发射功率设为最大时，对周边的通信链路干扰增强，故频谱效率性能较差。从仿真结果可以看出，提出的基于强化学习的联合波束成形和功率控制算法的频谱效率随着训练过程逐渐提高，即随着训练深度Q网络权重的不断更新，决策策略得到了优化。

图6为毫米波通信环境中不同用户数量时的频谱效率。从图中可知，当蜂窝网络中的通信链路数量增加时，笔者所提算法仍能够在大约3 500次迭代后收敛。结合图5可知，随着小区内通信链路的增加，小区间干扰程度提升，故算法的频谱效率降低，但笔者所提算法的频谱效率仍然为最优。

图7展示小区内用户数为3时不同天线数量下所提算法的频谱效率。由图7可知，天线数量为N=8时算法在大约5 000次迭代后收敛，N=64时算法在大约7 500次迭代后收敛。这是由于随着天线数量增加使计算复杂度增高，从而导致收敛速度的变慢。但随着天线数量的增加，算法的频谱效率随着天线数量的增大而提升。这是由于在天线数量较少时，波束主瓣较宽，不能精确地对准接收端，使得传输路径上的增益较小。当天线数量增大时，波束主瓣较窄，可以有效地指向信号路径。

5 结束语

笔者提出了一种基于强化学习的联合波束成形和功率控制算法，旨在无需CSI情况下最大化通信链路的频谱效率。问题为非凸，故将问题分为波束成形和功率控制两个子问题。首先提出信息交互协议助于基站进行信息交互了解环境信息，并设计基于深度强化学习的双模型系统求解联合优化问题。然后采用深度Q网络设计波束成形矩阵，并用DDPG根据波束成形矩阵对功率控制问题进行求解。仿真结果表明，在多用户通信环境，该算法的频谱效率优于传统波束成形算法和基于深度Q学习的联合波束成形和功率控制算法。