基于改进下垂控制的贯通同相系统负荷分配方法
2022-08-09周子博李兴城
田 旭,周子博,李兴城
(中国矿业大学(北京)机电与信息工程学院,北京市 100083)
0 引言
牵引供电系统承担着向电力机车提供能量的任务,是电气化铁道的重要组成部分[1-3]。目前,大多数国家的电气化铁路均为单相供电方式,为了减小三相不平衡度[4-6],相邻牵引供电臂通常采用公共电网不同相的电压来进行供电[7-8],因而存在电分相环节[9-10]。机车经过电分相时,会产生严重的过电压、过电流问题,导致电气化铁路无法安全稳定运行[11-12]。文献[13]提出利用电力电子技术在一个牵引变电站内实现同相供电,但相邻牵引变电站之间仍存在电分相,无法实现全线贯通。文献[14]提出了基于三相-单相的交直交变换器的贯通同相牵引供电系统。利用直流环节的隔离作用,使得公共电网与牵引网形成两个独立的异步交流电网,因而可以取消牵引变电站内的电分相,同时取消了牵引变电站间的电分相,实现牵引网全线贯通同相供电。
在贯通同相供电系统中,相邻牵引变电站同时为机车负载供电,机车与相邻牵引变电站间的线路阻抗及各牵引变电站分担的负荷功率均随着机车的运行位置变化而变化。当某一牵引变电站附近机车较多时,负载功率可能超出牵引变电站变流器的容量,导致变流器过载。因此,需要提出一种新型控制策略,不仅能将负荷功率合理地分配给各牵引变电站,还能使牵引变电站的输出功率保持恒定。
文献[15]分析了同相供电系统的阻抗特性与下垂特性,提出采用传统下垂控制的方法实现负荷均分,减少环流。文献[16]提出了一种有界下垂控制器,提高了其对数值误差和外部干扰的鲁棒性,但是没有考虑逆变器输出阻抗与线路阻抗对负载分配的影响。文献[17]改进了传统下垂控制方法,并考虑了线路阻抗与逆变器等效输出阻抗对功率的影响,但由于线路阻抗中含有电阻与电抗两种分量,导致下垂算法中存在功率耦合关系,致使功率无法精确分配。文献[18]采用了自适应虚拟阻抗的控制方法,提高了系统的动态响应能力和稳定性。以上文献均假设线路阻抗为固定值,但是在机车运行时,线路阻抗随机车位置发生变化。所以,上述方法都不适用于贯通同相供电系统。
本文研究了当线路阻抗随机车位置变化时,贯通同相供电系统的负荷分配方法,主要创新点有:
1)提出了新型自适应虚拟阻抗控制策略,包含自适应变化的电阻与电抗,用以补偿线路的变化量,改善了控制效果。其中,变化的电阻还可抵消线路电阻,以消除下垂控制中的有功功率与无功功率的耦合关系,提高功率分配的精度。
2)提出了改进型下垂控制策略。在下垂控制中加入比例-积分-微分(PID)动态补偿项,动态补偿项随负荷实时变化,提高了下垂控制的动态响应能力,使功率分配更加精确。
3)对改进后的下垂控制进行功率分析,通过改变下垂系数与虚拟阻抗,实现了相邻牵引变电站间负荷任意分配的目标。
1 贯通同相牵引供电系统建模
图1 为贯通同相供电系统示意图,三相电网通过变压器降压后接入三相整流器,整流出的直流电压经过单相变流器逆变后供给机车负载。

图1 贯通同相供电系统示意图Fig.1 Schematic diagram of interconnected co-phase power supply system
整流侧三相整流器的控制目标是维持直流电压恒定,逆变侧的控制目标是牵引网电压。本文研究的是相邻牵引变电站之间的负荷分配方法,主要对逆变侧变流器进行控制,逆变侧的拓扑结构不是本文研究重点。所以,一方面忽略整流侧,仅考虑逆变侧;另一方面,逆变侧采用H 桥拓扑结构。
不失一般性,以2 个牵引变电站为一辆机车供电为例,进行分析。由戴维南定理,可以将牵引变电站等效为电压源与阻抗串联的形式,建立的模型如附录A 图A1 所示。其中,E1∠φ1、E2∠φ2分别为逆变器1、2 的等效输出电压;负载电压U̇o=Uo∠0°,取其为参考电压,相位为0°;Zc1、Zc2分别为逆变器1、2的等效输出阻抗;ZL1、ZL2分别为机车负载与牵引变电站1、2 间的线路阻抗;ZLoad为机车负载;İ1、İ2分别为牵引变电站1、2 的输出电流。
牵引变电站采用的电压电流双环控制框图如附录A 图A2 所示。图A2 中,uoref为输入参考电压;kPWM为脉宽调制比;L、C和r分别为滤波电感、滤波电容和电感等效内阻;uo、io分别为逆变器输出电压和电流。
由图A2 可知,系统传递函数为:
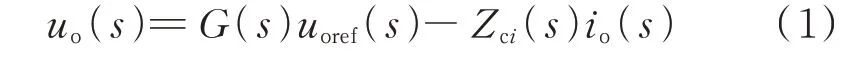

式中:Zci(s)为逆变器i的输出阻抗,i=1,2,下文同;G(s)为传递函数,则G(s)uoref(s)为逆变器的等效输出电压;GU(s)为电压环传递函数;GI(s)为电流环传递函数;KI为电流环比例系数;KU为电压环比例系数;ω0为谐振角频率;ωc为截止角频率;Kr为谐振积分常数。
根据式(1),逆变器输出电压与输出阻抗仅与主电路参数和控制参数有关。假设两牵引变电站中变流器的主电路参数与控制参数一致。则φ1=φ2,

经化简后有功、无功功率分别为:

式中:Ri为牵引变电站i与机车间的总电阻,Ri=Rc+RLi;Xi为牵引变电站i与机车间的总感抗,Xi=Xc+XLi。
由式(9)、式10)可知,牵引变电站1 输出的功率随机车与牵引变电站1 间距离的增加而减少,牵引变电站2 输出的功率随牵引变电站2 与机车距离的减少而增加。
2 传统下垂控制下的负荷分配效果分析
传统电力系统中电抗远大于电阻且为固定值。此时,输出电压的幅值和相位与输出功率的关系为:

对比式(11)、式(12)与式(14)、式(15)可得:
1)贯通同相供电系统中,线路阻抗Ri和Xi均与距离有关,为变化值,不满足传统下垂控制的使用条件。
2)考虑电阻时,各牵引变电站输出的有功功率和无功功率与输出电压的相位和幅值均有耦合关系,影响功率分配精度。
进行仿真验证时,假设牵引变电站1 与2 的容量一致,均为22 MW,机车功率因数为0.95。牵引网单位长度线路阻抗Z=(0.139 9+j0.333 5)Ω/km,仅使用传统下垂控制进行功率分配的效果如图2所示。

图2 相邻牵引变电站输出功率与距离之间的关系Fig.2 Relationship between output power and distance of adjacent traction substations
使用下垂控制后,有功与无功功率并不能达到恒定状态。随着机车的运行,有功功率间的差值逐渐增大,并且由于线路阻抗中电抗约为电阻的6 倍,无功功率的差异更大。
可知,在贯通同相供电系统中,仅使用传统下垂控制策略无法实现功率的精确分配,更加难以将负荷任意分配给两牵引变电站。
3 自适应虚拟阻抗与改进下垂控制
由前文分析可知,贯通同相供电系统仅使用传统下垂控制策略时,存在以下问题:1)由于线路阻抗变化,且有功功率与无功功率存在耦合关系,输出功率无法均分;2)传统下垂控制仅含比例项,功率分配不够精确;3)无法实现负荷在两牵引变电站间任意分配。针对这些问题本文采用以下解决办法:
1)针对阻抗变化问题,本文在控制策略中加入自适应虚拟阻抗环节[22-24],补偿由机车运行位置变化而引起的线路阻抗变化。同时,引入利用自适应虚拟阻抗中的虚拟电阻部分抵消线路阻抗中的电阻分量,减少耦合,提高功率分配精度,使各牵引变电站输出功率能够被均分。
2)改进了传统下垂控制,在下垂控制中加入补偿项,使负荷分配得更加精确。
3)基于改进下垂控制进行功率分析得到影响两牵引变电站间负荷分配的因素,通过改变下垂系数与虚拟阻抗,达成负荷按任意比例分配的目标。
3.1 自适应虚拟阻抗设计
引入自适应虚拟阻抗的控制框图如附录A 图A3 所示。图中Zv(s)为虚拟阻抗,为输出电流对输出电压的负反馈。
引入虚拟阻抗后系统传递函数为:

此时,通过改变虚拟阻抗可以改变变流器输出阻抗,进而改变等效线路阻抗。
设置ZT(s)=lZ'(s)=RT+sXT,ZT(s)为线路总阻抗,为了补偿阻抗变化,消除有功与无功功率的耦合关系,设计自适应虚拟阻抗为:

通过加入自适应虚拟阻抗,补偿了因机车运动而导致的线路阻抗变化,各牵引变电站输出功率将由变化量转化为恒定量。
当多辆机车在两牵引变电站间运行时,电路如附录A 图A4 所示。根据电路原理中的二端口网络相关理论:任何无源的二端口网络都可以等效为T型电路或者Π 型电路,本文等效为T 型电路,如附录A 图A5 所 示。
变换后的电路与一辆机车时相似,仍可采用本文给出的方法进行虚拟阻抗设计。
3.2 改进下垂控制策略
加入自适应阻抗后,各牵引变电站输出功率为:

式中:mai、mbi、nai、nbi分别为无功功率、有功功率的比例、微分下垂系数,可以改善下垂控制的动态特性;kqp、kqi、kqd、kpp、kpi和kpd分别为无功和有功功率控制补偿项中的PID 参数;Q*与P*为补偿项;Qav和Pav分别为各并联支路无功和有功功率平均值。
改进后的下垂控制加入了动态补偿项Q*与P*,通过PID 控制器对反馈信号进行处理后,提高了电压及频率的动态响应能力,从而改善功率控制环,使功率更加精确分配。
3.3 负荷分配策略
式(23)中的补偿项对于负荷分配的影响较小,可忽略不计,至此根据式(21)至式(23)可画出功率控制框图。
由附录A 图A6 可得,系统达到稳态时输出的有功功率为:

由式(24)、式(25)可知在等效线路阻抗为纯电感时,逆变器输出的有功功率与线路感抗无关,仅与有功下垂系数有关。稳态时无功功率与线路感抗和下垂系数有关。为了实现各牵引变电站间负荷任意分配,由上文分析可得,对于有功功率,可设置:

随着比例系数k的改变,两牵引变电站间的负荷分配也会发生变化。
考虑到机车位置的实时检测具有滞后性,设机车位置检测的采样间隔时间为Ts,本次检测及上次检测到的机车位置分别为d和d',则机车速度可表示为v=|d2-d1|/Ts。
如果机车位置检测的滞后时间为Td,则机车位置检测误差为Δd=|d2-d1|Td/Ts。此时,只需要在虚拟阻抗中补偿误差距离即可,将自适应虚拟阻抗式(28)和式(29)分别修改为:
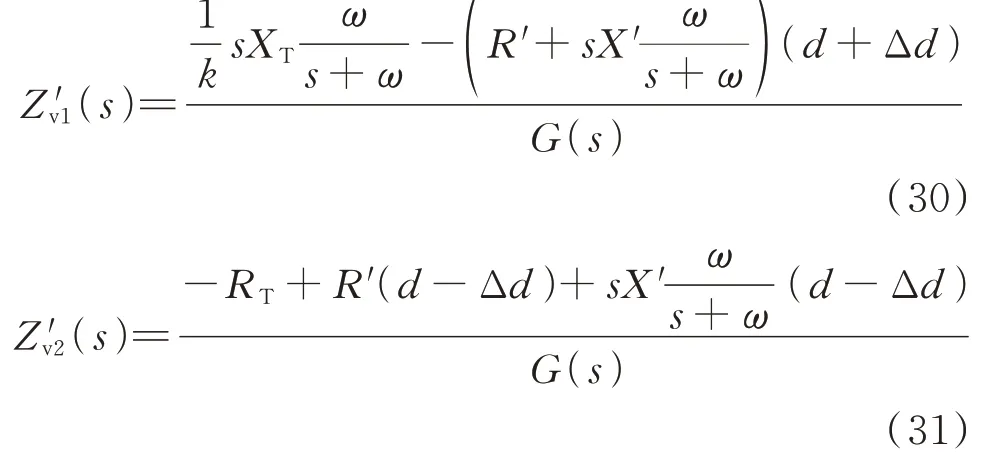
4 基于时变相量的小信号模型分析与下垂参数选取
下垂控制系统中的下垂参数选取与众多因素有关,计算较为复杂,当下垂参数选取过大时,会影响系统的稳定性,甚至造成系统崩溃。当下垂参数选取过小时,又会造成系统的稳态响应过慢[25]。因此本章将时变相量法应用到两牵引变电站并联系统的建模中,建立基于时变相量的小信号模型[26-27]。得到输出功率随频率、幅值变化的闭环控制模型。通过对模型的分析,得到一组稳定范围内的下垂参数。
由前面分析可知,为了改变负荷分配比例,需改变下垂系数,为了保持系统稳定性,本章所求下垂系数为拟选取的最大下垂系数。
附录A 图A8 为通过前文改进后的单牵引变电站等效模型。图A8 中,Rc、Lc为逆变器等效输出电阻和电感,LT为线路总电感。可得系统输出电压的时变相量表达式为:

式中:E、φ分别为系统输出电压幅值和相角;U为负载电压幅值。
利用小信号分析方法,在系统稳定工作点(E,U,φ)附近给一个很小的扰动量,对式(34)、式(35)进行线性化分析。根据式(21)、式(22)可得,加入虚拟阻抗后的P、Q分别只与φ、E有关,所以∂P/∂E与∂Q/∂E可以忽略。同时,考虑到并联系统中φ≈0 与E≈U,则有
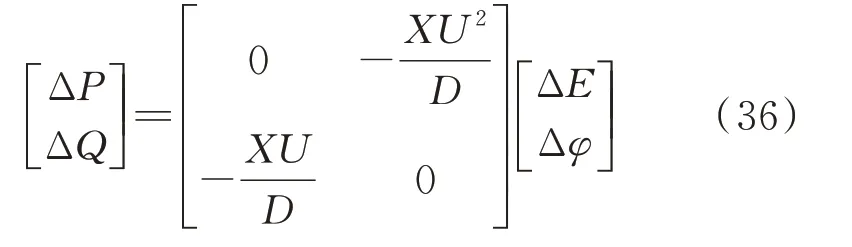
式中:ΔP、ΔQ分别为有功、无功功率变化量;ΔE为电压调节量;Δφ为相位调节量,Δφ=2π(f-fN),f为系统工作频率;D=(sLd+Rc)2+X2。
在并联系统中,由于系统扰动导致功率测量结果不够准确。因此,需要在式(34)、式(35)中的下垂控制算法的功率计算处添加一个滤波器,通常加入一阶滤波器1/(τs+1),τ=0.1。此时有

根据式(36)、式(39)可建立功率、电压、相角的闭环控制框图,如附录A 图A9 所示。分别可得ΔP和ΔQ关于Δδ和ΔE的闭环传递函数特征方程为:
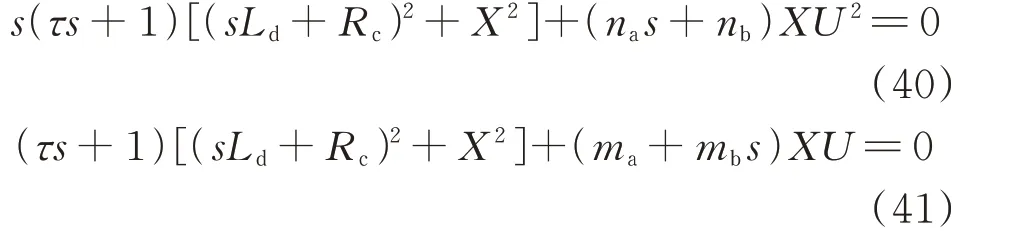
将表2 的数据代入式(40)、式(41),通过改变na、nb、ma、mb的值得到根轨迹示意图,如图3 所示。
图3(a)所 示 为na=2.5×10-7时nb变 化 的 根 轨迹。随着nb的增大,根轨迹λ1向右半平面移动,但一直处于系统左半平面内,对系统稳定性没有影响。当nb<1.327×10-8时,图中的两条根轨迹λ2与λ3均在右半平面上,为一对共轭根,系统不稳定。λ2与λ3的根轨迹随着nb的增大向左半平面移动,当nb>1.327×10-8时,λ2与λ3进入左半平面,系统稳定。
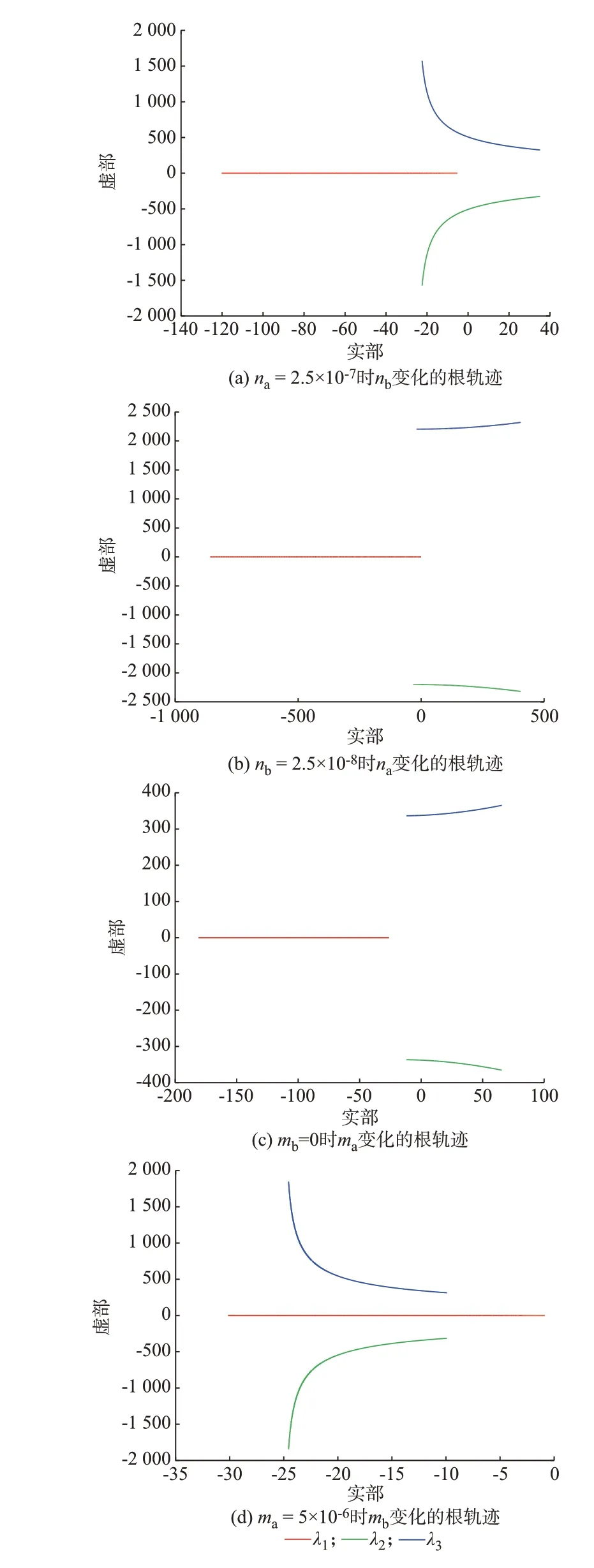
图3 根轨迹图Fig.3 Root locus diagram
图3(b)所示为nb=2.5×10-8时na变化的 根轨迹。其中λ1变化趋势与图3(a)相反,随着na的增大,λ1向虚轴靠近。图中另外2 条根轨迹λ2与λ3影响着系统的稳定性。当na>8×10-7时,λ2与λ3进入右半平面,系统不稳定。
图3(c)所示为式(33)中mb=0 时ma变化的根轨迹。增大ma会使λ1远离虚轴,即系统抑制扰动的速度更快。同时λ2与λ3会随着ma的增大向正半平面 移 动。当ma>6.37×10-5时,λ2与λ3进 入 正 半 平面,使系统变得不稳定。
图3(d)所示为ma=5×10-6时mb变化的 根轨迹。增大mb会使λ1远离虚轴,同时λ2与λ3会随着mb的增大向负半平面移动,系统一直处于稳定状态,故系数mb对系统稳定性无影响,其值取为0。
通过对时变相量的小信号模型进行分析,得到相关参数对系统稳定性的影响,本文结合实际需求选取的一组数据如附录A 表A1 所示。
5 仿真结果与分析
5.1 仿真参数
本文以2 个牵引变电站为例,在MATLAB/Simulink 中进行仿真,仿真模型参数见附录A表A2。
5.2 仿真结果与分析
为了便于展示负荷分配情况,假设机车在两牵引站间共运行50 km。未加改进时两牵引变电站工作情况如图4 所示。
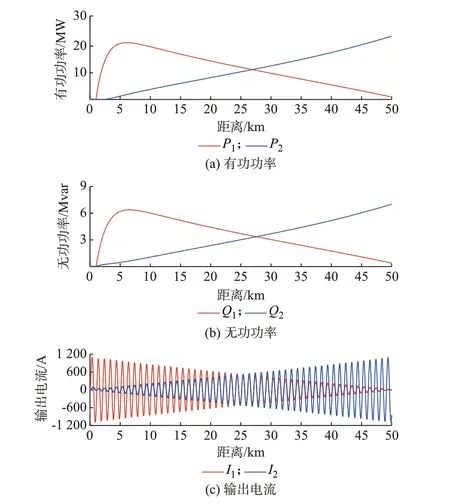
图4 未加虚拟阻抗及改进下垂控制策略工况Fig.4 Operation condition without virtual impedance and improved droop control strategy
由图4 可见,未加改进时,由于线路阻抗的变化,两牵引变电站有功与无功功率分别呈线性上升与线性下降的趋势,与理论分析相同。图4(c)为两牵引变电站的输出电流,波形具有对称性。
图5 所示为采用改进策略、k=1 且突加负载后各牵引变电站功率分配效果及输出电流波形图。

图5 k=1 且突加负载时采用虚拟阻抗及改进下垂控制策略后工况Fig.5 Operation condition with virtual impedance and improved droop control strategy when sudden load is added and k=1
为验证控制策略带负载的能力,在机车运行至20 km 时向系统突加视在功率为11 MW,功率因数为0.95 的负载,在运行至35 km 时切除增加的负载。相对于图4 未加改进前,改进后的控制策略明显提高了无功功率与有功功率分配精度,两牵引变电站输出电流也保持稳定。而且在投入与切除负载时,仍能保证有功功率与无功功率的分配精度,输出功率与输出电流可以快速达到稳定状态。由此可以验证加入了控制策略后的贯通同相供电系统,不但功率分配精确,而且在负载变化时功率分配的动态响应速度较快。
为了观察改变负荷分配比例瞬间控制策略的稳定性,仿真设置运行距离d=20 km 时,k由2 变为3,d=35 km 时,k从3 恢复至2。由图6 可知,改变分配比例前各牵引变电站输出功率与输出电流比均为2∶1 且保持稳定,在机车运行至20 km 时,分配比例改变,输出功率与输出电流均发生变化,但是由于加入了改进下垂控制,均能在运行3 km 后达到3∶1 的稳定状态。运行至35 km 后k由3 变为2 时,系统也能很快恢复稳定状态。由此可以验证,控制系统可根据牵引变电站容量的变化自动分配负荷,且动态响应较快。
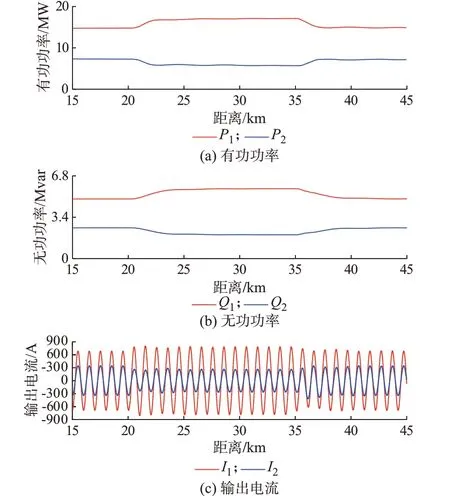
图6 k 改变时采用虚拟阻抗及改进下垂控制策略后工况Fig.6 Operation condition with virtual impedance and improved droop control strategy when k is changed
6 结语
本文对贯通同相供电系统负荷分配控制方法进行研究,提出了基于自适应虚拟阻抗的改进下垂控制策略,实现了负荷在线路阻抗变化时任意精确分配。
1)传统的下垂控制策略无法实现两牵引变电站间的负荷任意分配。
2)提出了自适应虚拟阻抗,在输出电流的反馈环中加入虚拟阻抗,虚拟阻抗的值随着机车运行距离自适应变化,补偿了线路阻抗的变化,使两牵引变电站的输出功率恒定。
3)提出改进下垂控制,对基于虚拟阻抗的下垂控制进行功率分析,通过改变下垂系数与虚拟阻抗实现两牵引变电站间的负荷任意分配。同时在下垂控制中引入补偿项,使功率分配更加精确。
4)对系统建立基于时变相量的小信号模型,通过对模型进行分析,得到下垂参数。
5)进行了不同负载和不同分配比例下控制系统的仿真验证,结果表明,负荷功率分配精确且动态响应较快。
本文主要研究相邻牵引变电站之间的负荷分配方法,分析时逆变侧采用H 桥拓扑结构。下一步将基于实际的贯通同相供电系统逆变侧拓扑结构进行仿真,研究不同拓扑结构对功率分配精度的影响。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
