面向负荷特征分析的地理分布式协同聚类方法
2022-08-09刘家丞刘鹏远徐占伯李晓鹏管晓宏
刘家丞,吴 江,刘鹏远,2,徐占伯,李晓鹏,管晓宏
(1. 智能网络与网络安全教育部重点实验室(西安交通大学),陕西省西安市 710049;2. 国网陕西省电力公司西安供电公司,陕西省西安市 710048)
0 引言
近年来,能源互联网架构下的电力数据资源急剧增长[1]。电力大数据分析具有从用电客户精确定位,到电力生产反馈指导,再到国民经济精准还原的全方位价值[1-2]。大数据技术在智能电网中的应用主 要 集 中 在 需 求 响 应[3-4]、负 荷 预 测[5-7]、故 障 诊断[8-9]、异常用电检测[10-11],还可用于研究电动汽车充电站部署[12]、光伏设备技术性能分析[13]等新兴负荷问题。
电力系统天然呈现分布式特征,在供给侧和需求侧都有所体现。供给侧方面,电网接入了众多分布在全国各地的微电网和发电站[14];需求侧方面,诸如居民用电、商业用电多离散分布在各城市中,其用电数据通常存储在不同地理位置的电力数据中心[15]。
在区域电网背景下,应用机器学习进行电力大数据分析,若采用独立式训练会由于样本数据量少导致结果差;而集中式训练对于具有分布式属性的电力大数据,则需进行跨中心的数据调度。因此,当数据量急剧增加时会产生以下3 个问题[16],使得传统的集中式机器学习在分布式大数据环境下不可行。
1)隐私保护问题
在智能电网中存在许多隐私保护的问题[17],例如智能电表收集到的负荷数据可以用于监测电网状态[18],然而从截获的数据中可以辨别出用户的活动,使得用户隐私受到威胁[19]。电网通常对传输的数据进行加密来保证其安全性,但仍有密钥管理等问题[20]。
2)数据时延问题
数据在网络中传播需要经过多个转发节点,导致数据时延,短时间进行大量数据的传输更会加重时延。满足使用需求的拓扑设计模型已经被提出[21],但数据越多,传输时延越大,可能会造成电网的控制性能恶化,带来更大的成本[19]。
3)传输成本问题
电网大数据进行跨数据中心的传输会占据大量的稀缺带宽资源[22],并且跨数据中心传输的成本远超在一个数据中心内进行传输的成本[19]。
为避免以上问题,同时实现区域电网下多地理节点的负荷特性分析,本文研究了地理分布式情景下的负荷特征聚类算法。针对隐私保护问题,采用基于主成分分析(PCA)-负荷指标的特征加权组合算法,提取原始数据的抽象特征,实现用户数据脱敏。考虑地理节点之间的拓扑关系,设计基于参数共识的分布式聚类算法,使数据中心之间仅传输极少量的拓扑特征,降低数据时延,并可构建全局聚类模型。针对传输成本问题,搭建考虑特征迁移的迁移学习框架,在原有模型基础上快速构建新模型,减少跨数据中心的交互次数。本文选取爱尔兰电网和中国北方部分城市电网的实际负荷数据进行测试,验证所提地理分布式协同聚类算法的有效性。
1 地理分布式协同聚类模型
能源互联网架构下,电力系统覆盖全国千家万户,电力数据也在电力用户与电网的交互中不断产生。为了最大限度减小基础服务设施与电力终端用户之间时延以及方便监管区域电力用户,电力数据中心通常分散建立在不同地理位置的各个城市中,呈现典型的地理分布式属性[23]。然而,考虑到数据的隐私保护问题,这些数据中心通常相互独立存储、独立维护,彼此间难以相互通信,形成了电力数据孤岛。针对这类处理地理分布数据集的机器学习应用,可以称之为“地理分布机器学习”[23]。相较于传统分布式针对复杂问题分而划之解决,地理分布式更注重在克服地理隔离的困难下搭建模型。
传统聚类模型的构建,通常需要一次访问多个区域的数据,考虑到隐私保护及传输成本等问题,原始数据难以在各电力数据孤岛之间进行通信,往往仅能传输少量脱敏信息,如模型参数等[24]。本文针对数据孤岛背景下的数据中心提出了地理分布式协同聚类框架,该框架允许地理分布式数据中心在仅传输少量脱敏参数的情况下独立搭建聚类模型,使得每个数据中心都能生成一个具有全局信息的聚类模型,且不同的聚类模型受不同地理位置影响呈现地理分布式特性,如图1 所示。
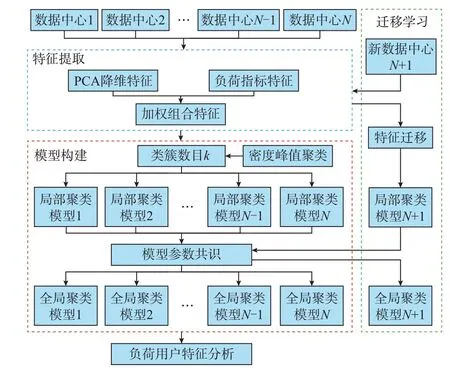
图1 地理分布式协同聚类框架Fig.1 Framework of geo-distributed collaborative clustering
第2 至4 章将分别阐述图1 所展示特征提取模块的特征加权组合算法、模型构建模块中考虑密度峰值信息[25]的分布式聚类算法以及迁移学习模块的特征迁移算法。
2 基于PCA-负荷指标的特征加权组合算法
在聚类模型构建之前,首先需要提取适合模型的负荷特征。特征提取一方面可以将原始的用户负荷数据抽象为难以理解的特征数据,实现数据脱敏、用户隐私保护;另一方面也可以降维压缩庞大的用户数据,大大减少传输成本。
本文采用将PCA 特征与负荷指标特征加权组合的方式,针对用户的月负荷数据进行特征降维提取处理,以两电网6 月数据为例,该数据原始维度为1 440 维。PCA 降维特征较为抽象,不能很好地说明原始数据的物理意义;负荷指标是先验知识,反映电力负荷的经验特性,但很多重要的抽象特征却无法体现。两类特征反映不同的特性,组合在一起可以获得更全面的负荷信息。
通过特征加权组合,电网6 月数据集最终的特征维度可压缩至12 维,相较于原始数据降低了1 428 维,极大减小了数据传输量,降低了传输成本。同时,文献[26]证明加权组合的特征聚类效果要显著优于单独使用以上二者时的结果。
3 基于参数共识的分布式聚类算法
各节点通过特征加权组合算法完成特征提取,即可将提取到的特征用于构建分布式聚类模型。分布式聚类算法的第1 步是在各节点进行密度峰值聚类,并借助多节点结果求众数,共同确定统一的聚类中心数目;第2 步是一个迭代过程,该过程首先采用K-means 算法进行一次聚类构建局部聚类模型并获得局部模型参数,接着通过参数共识算法使各节点模型参数交互计算并返回给原节点模型,最后各节点再根据返回的新参数进行一轮模型更新,此时完成一轮迭代。该算法会反复执行从局部聚类到模型更新的过程,直至整个模型收敛,最终每个节点都会得到一个全局聚类模型。接下来将逐步介绍本文模型中的密度峰值聚类算法、参数共识以及分布式Kmeans 算法。
3.1 密度峰值聚类算法
本文采用密度峰值的快速聚类(clustering by fast search and density peak,CFSFDP)算法[25]预先确定K-means 算法所需的类簇数目。对于每一个数据,该算法需要计算局部密度和相对距离这两个参数。当数据点局部密度和相对距离都大于其他点时,该数据点被定义为聚类中心,进一步地计算存在多少这样的数据点,从而可以确定类簇数目。
各节点首先采用密度峰值算法确定各自的类簇数目,随后统计所有节点类簇数目的众数,以该数作为之后局部聚类和分布式聚类的聚类数量,可以避免单个节点异常结果,该过程仅需在初始化时进行一次。本文选取一个典型节点绘制“局部密度ρ-相对距离δ”决策图。由图2 可知,有4 个点的局部密度和相对距离远大于其他数据点,最终本文确定类簇数目为4。
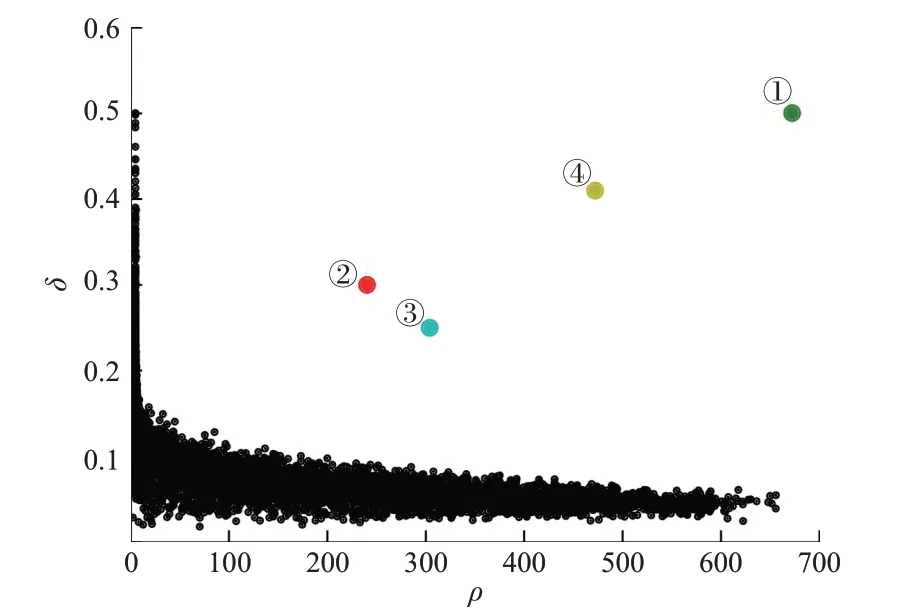
图2 CFSFDP 算法决策图Fig.2 Decision graph of CFSFDP algorithm
3.2 参数共识
考虑到单个数据节点独立聚类时,所用到的用户数量较少、类别较为单调,难以获得理想的聚类效果。参数共识算法可以将每个节点得到的模型参数进行整合,构建得到拥有所有节点特征的全局模型。该算法仅利用抽象的模型参数,实现了数据脱敏,同时极大压缩了传输数据,降低了数据时延。
参数共识是多个参与节点在预设规则下,通过节点信息交互,从而获得对各节点均适用参数的过程。该共识问题的数学表述如下:记加权无向图为G=(V,E,A),其边集和顶点集分别为E、V,边的加权邻接矩阵为A=(auv)。定义与节点v直接相连节点所组成的集合为Uv={u∈V:(u,v)∈E},zv为节点v的观测值。若对于节点v与u,存在zv=zu,则称v与u共识。进一步地,若图中所有节点v与j,均存在zv=zu,就称图G达到共识状态[27]。
本文中各节点采用的共识策略为平均共识。该算法获得的共识结果是各节点的参数均值,其中的加权邻接矩阵需为双随机矩阵,本文采用文献[28]给定的一种方式构造该矩阵,具体公式描述可见3.3 节。
3.3 分布式K-means 算法
分布式聚类模型主要基于K-means 算法,由局部聚类、参数共识、全局更新3 个阶段组成。Kmeans 算法的基本思想是将数据集中的所有数据划分为K个类别,使得不同类别的数据呈现较大差异,而同一类别中的数据表现相似。本文采用欧氏距离作为评价数据相似度的指标。
局部聚类阶段,各节点首先构建各自的局部聚类模型。记t时刻节点v的第k个聚类中心为cv,k(t),Cv(t)=[cv,1(t),cv,2(t),…,cv,K(t)] 为t时刻节点v的类簇中心集。基于传统K-means 算法的局部聚类模型在多地理节点背景下的表达式为[29]:

式中:Iv,k为节点v中属于类簇k的数据点集合。根据以上表达式即可完成局部聚类模型搭建。
参数共识阶段,首先需要在局部聚类模型的基础上计算得到数据总数与特征矢量之和这两个模型参数。记节点v在t+1 时刻属于类簇k的数据总数为Pv,k(t+1),矢量之和为Qv,k(t+1),表达式为:

式中:auv为节点v与节点u的邻接权重;ϕ为参数共识算法的迭代次数;A为拓扑图结构映射的邻接矩阵,表征地理节点之间的连接关系。
A矩阵借助随机数在以下两个条件的约束下计算构建[27]:一是A为双随机矩阵,其各行、各列之和皆为1;二是对于邻居节点u和v,需满足auv≥ξ,avv≥ξ,其中ξ为任意小的正数。经过快速迭代收敛,各节点的模型参数可以达到共识状态。
全局更新阶段,各节点获取参数共识后的模型参数,并通过该参数计算新的类簇中心。记共识停止步骤为Φ,并通过下式计算类簇中心cv,k(t+1):

经过上述3 个阶段,节点v完成了分布式聚类算法的一次迭代,之后算法会再次进行局部聚类到参数共识再到全局更新的整个过程。当算法达到规定迭代次数或cv,k(t+1)收敛时,该分布式聚类算法停止。实验证明分布式K-means 是可以收敛的[29]。
该算法在节点之间仅传输模型参数,即使被截获也无法获得用户信息,实现了数据脱敏,解决了用户隐私保护问题。此外,相较于原本需要在节点之间传输千万条数据,该算法仅需传输2 个参数数据,大大降低了数据时延。但是算法中的共识步骤增加了节点之间的交互更新次数,模型收敛速度有所降低,传输成本问题仍需进一步改善。
综上,本文所提分布式聚类方法首先采用PCA-负荷指标的加权组合算法对各节点用户负荷数据进行特征提取,随后通过密度峰值聚类确定统一的类簇数目。在此基础上,分布式聚类模型基于K-means 算法,以聚类中心作为共识参数,通过局部聚类、参数共识、全局更新3 个阶段反复迭代更新,直至模型收敛,最终各节点都可构建出适用的模型且模型的聚类中心一致。
4 基于迁移成分分析的迁移学习
当数据分布发生变化时,传统机器学习方法需重新进行建模,迁移学习则能够解决传统机器学习无法适用于训练集与测试集属于不同特征空间的问题[30]。本文采用迁移成分分析(transfer component analysis,TCA)算法进行迁移学习,使得新模型可快速迭代收敛,减少了各节点之间的数据交互次数,从而降低了传输成本。
TCA 算法是一种基于特征的迁移学习[31],可以解决源域与目标域数据分布不同的问题,其目的是将源域与目标域的特征变换到同一特征空间下使得二者近似服从相同的分布进行学习。在迁移学习之前,采用最大平均差异(maximum mean discrepancy,MMD)距离来评估源域与目标域之间的可迁移性。该距离最小为0,表征源域与目标域分布完全相同;距离大于1 表示可迁移性较差,易产生负迁移。TCA 算法中存在超参数优化问题,不同的超参数最终获得的结果也会有所不同。本文采用网格化搜索的方式,比对选取最好的迁移学习结果,从而确定合适的超参数[32]。
针对分布式聚类的迁移学习,当有新的数据中心融入该拓扑图中时,原拓扑结构将发生改变。一方面,对于新节点的数据,采用数据规约方法将其转换为与原有数据相似的范围,并通过与原有节点相同的特征提取方法获得新节点特征,随后计算新节点与原有节点之间的MMD 距离,当距离小于1 时判断源域与目标域之间具备可迁移性,并通过TCA算法使新节点与原有节点的特征近似服从相同的分布;另一方面,新节点将获得并采纳原先构建全局模型的模型参数,随后通过参数共识算法与其余节点重新进行迭代共识,直至新模型收敛。
5 算例分析
本文选取2010 年爱尔兰电网数据集CER[33-34]和2019 年中国北方部分城市电网负荷数据为研究对象,验证本文所提分布式聚类算法的有效性。其中,爱尔兰电网数据分属6 个独立的数据中心,共6 085 个用户,时间粒度为30 min;中国北方部分城市电网数据分属4 个独立的数据中心,共219 个用户,时间粒度为1 h。
5.1 算法收敛性验证
为更好验证算法的可行性,本文以全局数据点与类簇中心之间距离的误差平方和(sum of squared errors,SSE)作为算法收敛的判断条件之一,对比展示传统集中式K-means 聚类、无特征加权组合分布式算法与本文所提分布式K-means 算法聚类收敛情况,SSE 的计算表达式为:
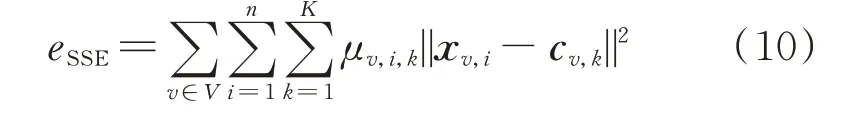
以爱尔兰电网6 月负荷数据为例,各类算法收敛情况如图3 所示。
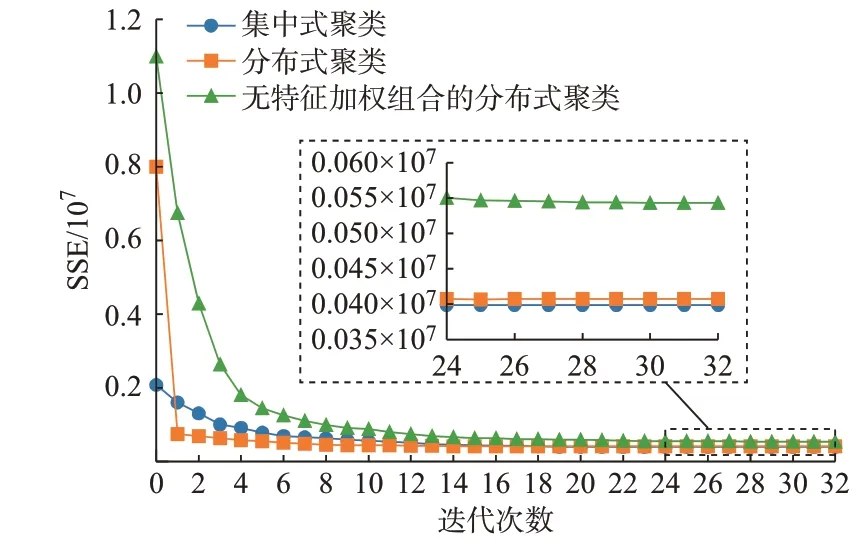
图3 算法收敛结果对比Fig.3 Comparison of algorithm convergence results
由图3 可见,3 种聚类算法均能在迭代一定次数后收敛,表明了分布式聚类算法的可收敛性。无特征加权组合分布式聚类的SSE 相较于分布式和集中式聚类收敛更慢,且收敛效果更差,验证了特征加权组合算法的有效性。同时,分布式初始的SSE 相较于集中式聚类算法大,但经过1 次迭代后能够断崖式收敛到与集中式聚类相近甚至相同的位置。这是因为多个独立分布的数据节点由于局部信息不同,初始化类簇中心时也会有非常大的差距,经过1 次参数共识,各节点利用大区域特征达到共识状态,从而实现加速收敛。
5.2 不同方法聚类效果对比分析
为验证分布式聚类算法的有效性,本文对比分析了不同算法聚类结果情况,算法包括集中式聚类、分布式聚类、独立式聚类、基于密度的有噪空间聚类(density-based spatial clustering of applications with noise,DBSCAN)、层次聚类和分布式密度聚类(density based distributed clustering,DBDC)[35],其中独立式聚类算法是指各个节点仅进行局部聚类而不进行参数共识。考虑到不同类型电力用户的负荷偏度和负荷散度之间具有较大差异,根据这两个指标可以更直观地区分不同用户[26],因而图4 选取了负荷数据中负荷偏度和散度作为横纵坐标,以爱尔兰电网2010 年6 月与中国北方城市电网2019 年6 月负荷数据为例,绘制3 种算法对用户负荷的分类情况。爱尔兰电网结果如图4 和附录B 图B1 所示,中国北方城市电网结果见附录B 图B2 和图B3。
由图4 可以看出,集中式、分布式和层次聚类算法都能很好地将用户负荷分为4 种类型(Ⅰ、Ⅱ、Ⅲ、Ⅳ型),且4 种类型之间的界限较为明显;DBSCAN和DBDC 算法能将用户有层次地分为4 种类型,但类型界限不清晰且噪声点过多;而独立式聚类结果非常差,类簇之间差距很小,难以看出用户分类情况。分析其原因在于DBSCAN 和DBDC 算法根据样本间距和样本密度逐步寻找类簇,而电力用户数据样本密度不均匀且间距差较大,导致很多高耗能的工商业用户易被识别为噪声点。DBDC 算法更是由于地理节点样本数量少、间距大且节点之间没有进行有效通信,难以进行有效聚类。而独立式聚类中,各个节点仅利用各自的局部信息进行分类,而局部信息本身由于地理分布不同,导致各节点局部信息之间差异较大,进一步影响了聚类结果。对比图4 与附录B 图B1 至图B3 可以看到,分布式聚类得到的结果和集中式聚类基本相同,且分布式聚类中各节点模型基本一致,是因为分布式聚类采用了参数共识策略,各节点之间能够有效传递不同的区域特征,使得每个节点最终都享有全局信息,并能收敛得到很好的聚类模型。为了更量化地反映各个聚类模型所得结果的差异性,本文对6 种聚类模型采用轮廓系数(silhouette coefficient,SC)、戴维森堡丁指数(Davies-Bouldin index, DBI) 、 CH (Calinski-Harabasz,CH)指标和邓恩指数(Dunn validity index,DVI)衡量对负荷用户分类的效果。SC 综合了内聚度和分离度两种系数,其数值范围为[-1,1],越接近于1,效果越好;DBI 计算类簇内平均距离和类簇之间最小距离的比值,该值越小,聚类效果越好;CH 指标计算类簇内各点与类簇中心的距离平方和来评估类内的紧密程度,该值越大说明类簇自身越紧密;DVI 综合衡量簇内和簇间距离,其值越大说明聚类效果越好。以爱尔兰电网2010 年6 月与中国北方部分城市电网2019 年6 月负荷数据为例,进行20 次实验并取各指标的均值,不同算法聚类结果的性能指标和计算时长见附录B 表B1。

图4 CER 聚类结果Fig.4 Clustering results of CER
由附录B 表B1 可知,本文所提分布式聚类多数指标都能达到最佳,集中式与分布式协同聚类算法结果相近,层次聚类法各项指标居中,而独立式聚类、DBSCAN 和DBDC 结果最差,证明分布式聚类算法可以通过参数共识步骤实现数据集中训练并获得较好的效果。从DBI 簇间指标来看,层次聚类能够实现非常好的不同簇间划分,分布式和集中式聚类的簇间划分次之;从CH 簇内指标来看,分布式聚类簇内划分最好,集中式划分次之,层次聚类簇内划分稍差;从SC、DVI 综合指标来看,分布式和集中式聚类能够很好地平衡簇内和簇间距离,实现优质分类,层次聚类综合而言没有分布式K-means 算法好,而独立式聚类、DBSCAN 和DBDC 在样本数据量小、样本间距较大的情况下表现最差。从算法耗时来看,分布式聚类的计算时长远小于集中式聚类和DBDC 算法,略大于独立式、层次聚类法和DBSCAN 算法。集中式聚类由于所用数据量较大,多次迭代计算耗时也较大;DBDC 算法为了实现分布式聚类进行了多次划分导致计算耗时增大;层次聚类和DBSCAN 仅进行一次聚类或划分,算法复杂度小,因而耗时最少;分布式和独立式聚类的单节点数据量小,计算耗时也较小。
进一步对比集中式和分布式聚类算法数据传输量和时间的不同,如附录B 表B2 所示。可以很明显看到,分布式聚类的数据传输量约是集中式的千分之一,传输速度比集中式快约3 000 倍。因为分布式聚类在各节点之间仅传输两个脱敏的模型参数,实现了用户数据隐私保护的同时也大大降低了数据的传输时延。但相较于集中式仅需传输一次数据,分布式聚类由于共识算法需要多次传输迭代,增加了模型构建时间。然而分布式仅比独立式聚类慢约1 s,这也证明了参数共识步骤耗时极小。
综上结果可以看出,在地理分布式的背景下,分布式聚类算法综合簇内和簇间的划分最好,实现了数据脱敏并减少了传输成本,且计算速度远快于集中式聚类和DBDC 算法。
5.3 模型可迁移性验证
为验证算法的可迁移性,选取爱尔兰电网和中国北方部分城市电网负荷数据分别进行分布式聚类并将聚类结果简单拼接到同一坐标中,如附录C 图C1 所示。可以看出,两地电网用户分布不同,具有不同的区域地理特征。以爱尔兰电网数据作为源域,中国北方部分城市电网数据作为目标域,计算两者之间的MMD 距离为0.112,证明两地数据特征分布有所不同且具备可迁移性。接下来将对两地数据集采用TCA 算法进一步验证模型可迁移性。
选取爱尔兰电网负荷数据先构建包含6 个地理节点的分布式聚类模型,随后将中国北方城市电网4 个地理节点的负荷数据依次加入拓扑图中作为新加入的地理节点,分布式聚类模型类簇中心移动迁移情况如附录C 图C1(d)所示,迁移前后评价指标见表C1。
对比图C1(c)和(d)可以看到,经过特征迁移后两地电网中均有部分用户的归类发生偏移且类簇中心也有轻微偏移,最终可以收敛得到容纳两地数据的新聚类模型,说明分布式聚类迁移学习具有很好的效果。根据附录C 表C1,特征迁移后DBI、CH、SC 指标相较于迁移前略差,是由于两电网用户数据分布不同,经过特征迁移类簇中心发生移动,原有的小部分用户被重新分配导致指标略差。而MMD 距离迁移后趋近于0,说明两电网特征分布近乎相同,也证明本文所提分布式聚类算法能够在原有节点的基础上融入新节点实现在线快速聚类,可以较好地应用在迁移学习框架下。
5.4 聚类用户负荷特征分析
采用分布式聚类模型进行聚类,标记所得聚类结果每一类的类簇中心作为典型用电负荷用户,根据标记抽取原始负荷数据集的典型用户负荷数据,可以绘制出对应4 类典型负荷曲线进行分析,结果见图5 和附录D 图D1。

图5 分布式协同聚类典型用户负荷曲线Fig.5 Typical user load curves of distributed collaborative clustering
以电网6 月数据结果为例,如图5 所示,可以看出用户用电模式丰富多变,Ⅰ型用户负荷水平普遍很高,一般有两个高峰用电时段,集中在08:00—12:00 和14:00—18:00 时段,晚间仍有高负荷水平,属于高负荷部分迎峰用电;Ⅱ型曲线负荷水平比其他3 类都低且较为均匀,用电量基本不超过0.8 MW,高峰用电通常在06:00—09:00、12:00—14:00 和19:00—23:00 这3 个时段,属于低负荷迎峰用电;Ⅲ型用户日间08:00—19:00 时段的负荷水平较大,午间和晚间有负荷小峰值,夜间负荷水平急速下降,是典型的日间高负荷用电;Ⅳ型用户06:00—11:00 和14:00—19:00 时段负荷水平较高,夜间用电趋近于0,峰谷形态与Ⅱ型互补,属于低负荷部分迎峰用电。
采用本文所提的分布式聚类算法,可以清楚地将电网负荷用户划分成4 类负荷用户类型,为电网后期运行、规划打下基础,也证明了该算法的有效性和可行性。
6 结语
本文针对地理分布式背景下的电力数据,构建了考虑特征迁移的分布式聚类模型框架,提出了一种基于参数共识利用局部信息得到全局聚类模型的分布式协同聚类算法。算法针对单地理节点采用PCA-负荷指标获得加权组合特征,考虑密度峰值信息确定类簇数目,通过参数共识利用局部模型参数使得每一个电力数据中心获得包含全局信息的全局聚类模型。针对新加入的数据中心,采用TCA 算法进行迁移学习,实现在线构建分布式聚类模型。通过算法对比试验表明,本文所提的分布式协同聚类算法能够在地理分布式背景下借助少量脱敏数据传输,实现用户隐私保护,有效降低数据时延,同时能保留区域特征,并利用整体区域特征实现加速收敛、快速构建全局聚类模型,获得很好的负荷用户分类效果,帮助分析电力用户负荷特性。
然而,算法中的共识步骤需要节点之间多次交互迭代,传输成本问题仍有待进一步解决。此外,多个地理节点聚类数目要求一致的条件稍显苛刻,限制了方法的应用。在今后的研究工作中,一方面需要改善参数共识算法,减少节点之间交互;另一方面也需增强算法的灵活性,对不同地理节点不同聚类数目也可构建和迁移模型。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
