基于主成分分析的BP 神经网络粮食产量预测模型

钟 奇

（重庆师范大学数学科学学院，重庆 401131）

我国作为世界上人口最多的国家，始终贯彻把发展粮食生产放在社会发展的重要位置。我国粮食产量能满足人们的基本需求，但随着生活水平提高，人们对粮食的需求更多样化[1]。现阶段，我国耕地面积逐年减少，进行粮食产量预测迫在眉睫。粮食生产受众多因素综合影响，分析众多影响因素并构建粮食产量预测模型是一个值得探讨的问题。构建良好的粮食产量预测模型对国家宏观调控粮食政策、保障国民粮食需求都具有十分重要的指导意义。

目前，国内外对预测粮食产量问题的研究中，具有很强代表性的模型有3 种。①时间序列模型是根据长期的历史趋势数据对未来粮食产量进行分析预测，其中较常见的包括指数平滑法和灰色预测方法，这类模型的优点是简单易行且在短期内有较高精度，但不能体现变量因素对粮食产量的影响[2]。②回归模型能描述变量之间的内在联系，但易因变量选取不恰当造成较大的结果偏差。③神经网络模型是模仿人体神经元间关系建立的非线性模型，在粮食产量预测中有较好的应用价值。

采用BP 神经网络能较好地描述粮食产量的非平稳性，但算法可能陷入局部极值等[3]。粮食产量的影响因素之间具有复杂的联系，若考虑较多的影响因素，会增加问题的复杂程度，因此本文采用主成分分析法提取主成分，优化BP 神经网络，提高粮食产量预测精确度。

1 PCA-BP 组合模型

粮食生产受众多因素综合影响，通过主成分分析法有效降低多个影响因子之间信息的冗余程度，从而获得粮食产量与影响因子最全面真实的作用关系。在对粮食产量进行BP 神经网络预测前，先对粮食产量影响因子进行相关性检验，判定其是否可以采用主成分分析法。然后进行主成分提取，再进行BP 神经网络预测，基本步骤如图1。

图1 PCA-BP 神经网络基本流程图

2 BP 神经网络预测粮食产量

基于对上述BP 神经网络与PCA-BP 神经网络的理解，对比两种模型的有效性。

2.1 单一模型预测

影响粮食产量的因素众多，本文选取的影响因子包括粮食作物播种面积X1、有效灌溉面积X2、农业机械总动力X3、农用化肥施用折纯量X4、农村用电量X5、受灾面积X6、乡村就业人员X7和农村居民家庭人均纯收入X8[4]。

本文从《中国统计年鉴》中选取预测粮食产量所需数据，即1999—2018 年共20 年的粮食产量相关数据，将其分为训练数据和检验数据两个部分。在实验中调用MinMaxScaler 函数，对粮食产量相关数据归一化，采用最低值法调试，确定最佳隐含层单元数为7。BP 神经网络学习效率非常重要，学习效率太大会导致不稳定，太小会导致程序慢，其取值范围一般为（0.01，0.1），对学习效率进行不断调试，确定最佳学习效率为0.035。设置训练精度为0.004，采用1999—2013 年的粮食产量相关数据对网络进行训练。预测2014—2018 年的粮食产量，与真实数据进行比较，得到其相对误差，见表1。对结果进行分析，得到单一BP 神经网络能根据影响因素对粮食产量作出预测，但预测的误差较大，训练时间较长。

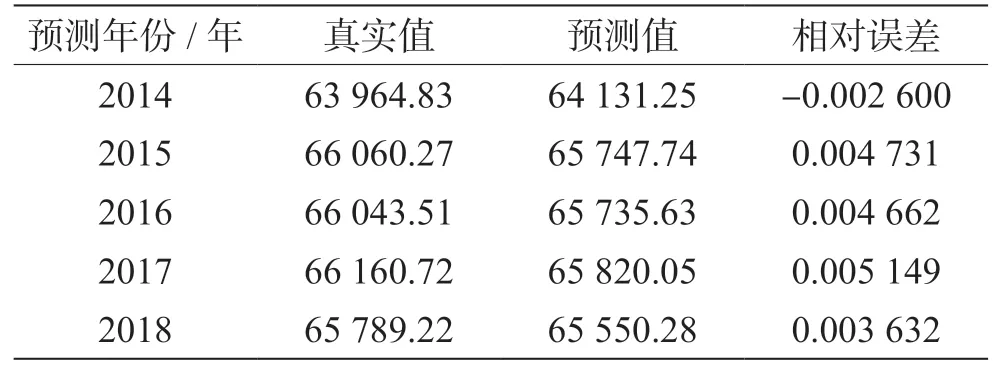
表1 预测值与真实值比较表

2.2 PCA-BP 组合模型预测

先对粮食产量影响因子进行标准化，再采用KMO 统计量和巴特利特检验，判定其是否能进行主成分分析。KMO=0.742 即众多影响因子之间具有较强的相关性，巴特利特检验的显著性概率为0 ＜0.01，即满足显著性的要求。

采用SPSS 进行主成分分析，使数据的基本特征保留下来。第一主成分和第二主成分的累积贡献率达到95.8%，说明这2 个指标可有效解释8 个粮食产量影响因子中95.8%的信息，表明2 个主成分的信息概况能力较好：

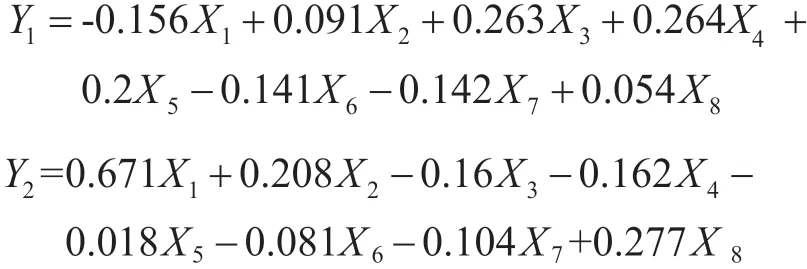
第一主成分在浇灌、机械总动力、化肥施用和用电量等方面的载荷较大，这些变量主要可以反映粮食生产的现代化水平；第二主成分在粮食作物播种面积和受灾面积方面的载荷较大，反映了粮食生产的基本保障，由此可以作为粮食有效播种面积。

将Y1、Y2即粮食生产现代化水平和有效播种面积这2 个主成分作为输入层的神经元。设置网络的隐含层为1，最佳隐含层单元数为5，其余参数与单一BP 神经网络一致，结果见表2。对结果进行分析，得到PCA-BP 组合模型能较好地实现粮食产量的预测，输入神经元个数从8 个降为2 个大大降低了模型的复杂度，预测的精度较好。

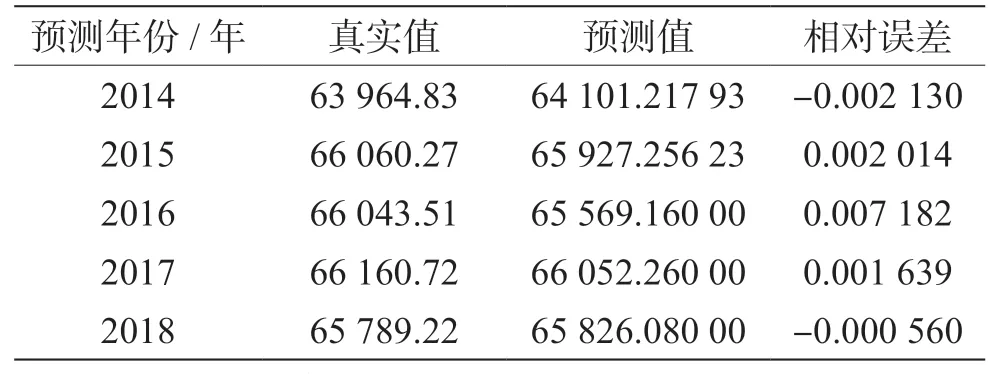
表2 PCA-BP 组合模型预测值与真实值比较表

2.3 模型的比较检验

根据以上预测结果可知，两种模型在粮食产量预测中都能较好地预测粮食产量。单一模型的输入神经元为粮食产量的8 个影响因子X1～X8，而组合优化模型的输入神经元为Y1、Y2，即粮食生产现代化水平和粮食有效播种面积，两个模型的输入神经元不同。为了更加直观比较两个模型的预测效果，对两个模型实验结果作图，见图2、图3。图2 表明组合模型比单一模型预测值更接近粮食产量的实际值。图3 中，在训练速度、精度相同的情况下，单一模型的收敛步长为200，PCA-BP 组合模型的收敛步长为100，减少了50%，大大提高了神经网络的运行效率[5]。

图2 预测结果对比图

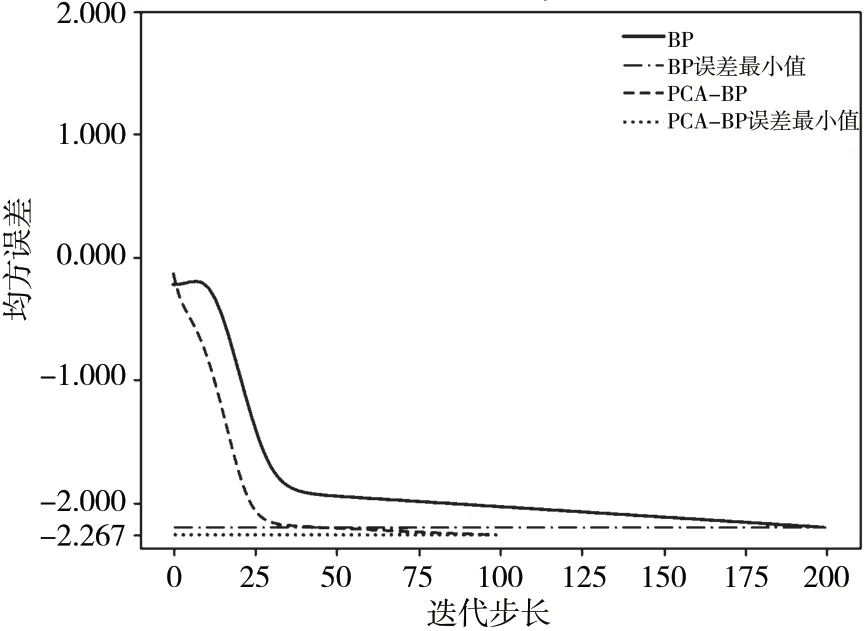
图3 预测误差对比图

如表3 所示，组合优化模型比单一模型平均相对误差减少0.002 394，说明组合优化模型在粮食产量预测上效果好。

表3 两个模型的误差对比表

3 结论

粮食生产始终是我国社会发展的重要问题，对我国粮食产量进行预测愈发重要。本文提出的PCABP 组合优化模型能很好地改善单一模型的学习速率较缓慢、算法可能陷入局部极值等问题。对粮食产量的影响因子进行相关性检验，判定其是否适合主成分分析，精炼粮食产量影响因子，得到影响因子的2 个主成分Y1、Y2，即粮食生产现代化水平和粮食有效播种面积，使输入层神经元由8 个变为2 个，简化了模型复杂度。仿真实验表明，PCA-BP 组合模型比传统模型的学习速度更快，预测误差更小，可推广到其他影响因素维度较大的预测中。