基于混沌-RF-SVM变形预测模型的隧道运营安全状况分析

黄阿岗,何 军，郝付军

(1.陕西铁路工程职业技术学院，陕西 渭南 714000；2. 河南理工大学，河南 焦作 454000)

近年，我国交通建设持续发展，隧道工程数量也日益增加，截止2018年底，公路隧道共计17 738处，总长约1 723.61 km；值得指出的是，隧道工程在带来巨大经济效益的同时，还带来一定的运营安全问题，因此，开展既有隧道的运营状况研究具有重要意义[1-2]。目前，已有相关学者开展了相应研究，如张霄等[3]利用物探法实现了运营隧道的岩溶病害探查；朱小明等[4]对运营隧道的仰拱缺陷进行了特征分析和处置技术研究；叶剑可等[5]开展了运营隧道的典型病害研究，并提出了相应的处置措施。上述研究虽已取得相应成果，但多偏向于运营隧道的定性研究，未涉及基于变形预测基础上的运营状况分析，进而仍需进一步拓展该方面研究。在隧道变形预测研究方面，赵淑敏[6]、张碧[7]验证了支持向量机适用于隧道变形预测，但值得指出的是，传统预测模型难以保证预测效果，需进一步拓展其优化处理研究，且单一模型的准确性有待验证，加之贺华刚[8]验证了M-K检验在隧道变形趋势判断中的适用性，可进一步利用该检验实现预测效果的可靠性验证。综合上述，以运营隧道变形监测成果为基础，先以支持向量机为理论基础，通过随机森林算法和混沌理论实现其参数优化，以构建合理的变形预测模型，并依据变形预测结果实现隧道运营状况分析；同时，再利用多种预测模型和M-K检验进行预测结果的可靠性验证分析，以佐证变形预测结果的准确性。通过该研究，旨在为既有隧道的运营状况分析提供一种新的思路，以奠定运营隧道安全评价的理论基础。

1 基本原理

文中研究思路可总体表述为：基于运营隧道变形监测成果，通过变形预测来评价其发展趋势，旨在为隧道安全运营提供一定的理论指导，主要包括变形预测过程和预测结果的可靠性验证过程。

1.1 变形预测模型的构建

SVM模型具有结构风险最小化原则，其思想可总结为：将低维空间的非线性问题映射成高维空间的线性问题。在SVM模型的应用过程中，可将其训练过程表示为：

yi=wTφ(xi)+b.

(1)

式中：yi为预测值；w为列向量；xi为输入信息；φ(xi)为激励函数；b为偏置向量。

由于SVM模型已被广泛运用于隧道工程领域[9-10]，因此，不再赘述其基本原理。

值得指出的是，SVM模型虽具有较强的适用性，但也存在一定不足，如激励函数类型相对较多，以往多随机确定，缺乏客观性；惩罚因子及核函数宽度参数直接影响SVM模型的学习能力和泛化能力，但其确定具较强的随机性。因此，为有效保证预测精度，需对上述两问题进行针对性优化处理。

1)激励函数的优化处理。在SVM模型的应用过程中，常用的激励函数有三类，包括多项式核函数、高斯核函数和Sigmoid核函数，三者的基本原理存在一定差异，适用性也随之不同，为实现其优化处理，将优化过程表述为：对三类激励函数进行试算筛选，预测效果最优者即为最优激励函数。

2)惩罚因子及核函数宽度参数的优化处理。由于随机森林算法(Random Forest, RF)具有较强的集成学习能力，优点突出，如泛化能力较强，不易出现过拟合现象；对噪声的容忍性较强，不易出现不平衡问题。因此，利用RF算法实现SVM模型的惩罚因子及核函数宽度参数优化处理是可行的。结合RF算法的基本原理，可将其寻优过程表述为：①先在N个原始样本中进行有放回的随机抽取，且随机抽取次数为N次；当N足够大时，单个样本不被抽取的概率为36.8%，因此，在原始样本中，不被抽取的样本作为袋外数据，用于评估模型的泛化误差。②每个随机的训练集将会生成对应的决策树，并在其每个节点处，会有m个特征被随机选出；按照不纯度最小原则进行m个特征的分裂处理，且在分裂过程中，影响因素的个数保持不变。③重复上述步骤k次，即会得到k个训练集及k棵决策树，进而形成随机森林；通过迭代寻优，所得最优决策树的寻优结果即为随机森林算法的最终寻优结果，将其赋值于SVM模型，进而完成惩罚因子及核函数宽度参数的优化处理。

前述优化处理虽有效保证了SVM模型参数的最优性，但由于运营隧道的变形数据具有较强的非线性特征，使得其预测过程也难以完全刻画其变形规律，即会存在预测误差；为进一步提高预测精度，且考虑到预测误差具有较强的随机性和混沌特征，提出利用混沌理论进行误差弱化预测。

首先，采用Lyapunov指数法求得混沌指数λmax，并利用其判断预测误差的混沌特征，判据为：当λmax>0时，说明预测误差具有混沌特征，可利用混沌理论实现误差弱化预测；反之，预测误差不具混沌特征。结合混沌理论的基本原理，将预测误差的弱化流程详述如下：

将前述优化SVM模型的预测误差表示为{εi,i=1,2,…,n}，并进行m维相空间重构处理，即：

ψi=[εi,εi+τ,…,εi+(m-1)τ]T.

(2)

式中：ψi为第i个相点；m为嵌入维数；τ为延迟时间。

由式(2)得出，欲进行相空间重构，需合理确定嵌入维数和延迟时间，据相关文献的研究成果[11]，两参数的求解过程为：

首先嵌入维数求解：假定初始值m0，计算得到相应的关联维数C(λ)，其与λ存在对数线性关系，即：

(3)

式中：d(m)为嵌入维数的函数表达式。

随m值增加，d(m)值具先增加再趋于稳定的特征，且当d(m)值趋于稳定时，拐点处的m值即为对应的嵌入维数。

其次，延迟时间求解：利用去偏复自相关法进行延迟时间参数的求解，先将延迟时间的相关函数C(τ)表示为：

(4)

式中：ε′为预测误差均值。

C(τ)值与τ值间具递减关系，当C(τ)值为1-1/e时，对应的τ值即为所求的延迟时间。

最后，在相空间重构基础上，再利用Lyapunov指数法进行预测误差的弱化预测，即以ψi为预测中心，求解与ψl相点(最近相邻点)之间的距离d：

(5)

欲完成预测误差的弱化预测，需保持d值最小，进而可类比反推出εi+1值，以实现误差弱化预测。

为便于后续分析，将预测模型进行类型划分，即：

模型1：未经任何优化处理的传统SVM模型。

模型2：仅经激励函数初步优化的SVM模型。

模型3：在激励函数优化处理基础上，再经RF算法优化处理的RF-SVM模型。

模型4：在模型3基础上，再利用混沌理论进行误差弱化预测的混沌-RF-SVM模型。

基于前述，旨在通过隧道变形预测来实现隧道运营状况分析，并将判据设定为：若隧道变形趋于稳定方向发展，则其后期运营状况将会维持现状；反之，隧道变形趋于不稳定方向发展，后期运营状况将会进一步减弱，不利于安全运营。

1.2 可靠性验证模型的构建

按照文中思路，可靠性验证共计可分为两个步骤：其一，利用多类其他模型进行类比预测，以验证预测结果的准确性；其二，是利用Manner-Kendall检验法进行运营隧道变形趋势性判断，以验证外推预测结果的可靠性。

步骤一的模型设定。为切实验证该文预测模型的优越性，提出的对比预测模型为BP神经网络模型和GM(1,1)模型，通过三类模型的预测效果对比来验证外推预测结果的可靠性。

步骤二模型的设定。由于M-K检验属非参数统计方法，操作较为简单，加之准确性高，进而利用其实现运营隧道的变形趋势判断是可行的。

依据M-K检验的基本原理，求得M-K检验的最终统计量Z：

(6)

式中：S为初步统计量；Var(S)为方差计算值。

当Z值大于0时，说明运营隧道变形呈增加趋势；反之，运营隧道变形呈减小趋势。同时，在相应检验水平a条件下，通过对比Z值与临界值Za间的大小关系，可进一步评价运营隧道变形的趋势等级和趋势程度，具体标准如表1所示。

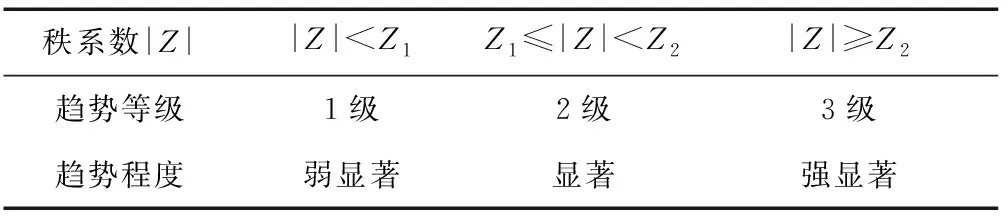
表1 运营隧道变形趋势等级及程度划分标准

2 实例分析

2.1 工程概况

嬉野隧道隶属长崎高速，于1990年5月开始施工，于1992年11月完工，纵向长度为683 m，但在施工完成后，隧道运营阶段经历历年变形，为保证运营安全，并有效掌握其变形状况，于1992年11月开展了隧道运营期的变形监测，监测项目包括沉降变形和水平收敛，监测频率为1次/2个月，共计得到28个监测周期的变形监测成果，经统计作图，得STA211+90断面的变形曲线如图1所示[12]。

图1 隧道运营期间的变形曲线

2.2 隧道变形预测分析

在运营隧道变形预测过程中，以1～23周期样本为训练样本，24～28周期为验证样本，外推预测周期数设定为4期；同时，为充分验证不同优化步骤的预测效果，以沉降变形为例，进行不同优化阶段预测效果对比分析。

首先，对不同核函数的预测效果进行试算统计，所得结果如表2所示。3类核函数的预测效果存在明显差异，其中，高斯核函数的平均相对误差值为2.64%，相对最小，说明其预测效果相对最优，其次是Sigmoid核函数和多项式核函数，因此，确定SVM模型的核函数为高斯核函数。

表2 不同核函数的预测效果对比 %

其次，再利用RF算法进行优化处理，并在其基础上，进一步利用混沌理论进行预测误差弱化预测，所得不同阶段预测模型的结果如表3所示。由表3可知，在相应验证节点处，模型1至模型4的相对误差值呈不同程度的减小趋势，说明通过递进优化处理，能有效提高预测精度，且在模型4的预测结果中，相对误差区间为1.86%～2.01%，变化范围较小，说明本文预测模型具有较好的稳健性。

表3 不同优化阶段的预测结果对比

为进一步分析4类模型的预测效果，再对4者的特征参数进行统计，得表4。据表4，在预测精度方面，由模型1至模型4的平均相对误差呈减小趋势，进一步验证了模型构建过程中递进优化处理的必要性，且模型4的平均相对误差为1.93%，具有较高的预测精度；同时，在预测结果的稳定性方面，由模型1至模型4的方差值也呈减小趋势，说明通过递进优化处理不仅能提高预测精度，还能提高预测结果的稳定性。

表4 不同优化阶段模型的特征参数统计

最后，再进行隧道沉降变形的外推预测和水平收敛预测，结果如表5所示。由表5可知，两监测项目的平均相对误差分别为1.93%和1.97%，进一步验证了预测模型不仅具有较高的预测精度，还具有较好的稳健性；同时，由外推预测结果可知，隧道变形具持续增加趋势，但增加速率趋于减小，说明隧道变形大致趋于稳定方向发展。

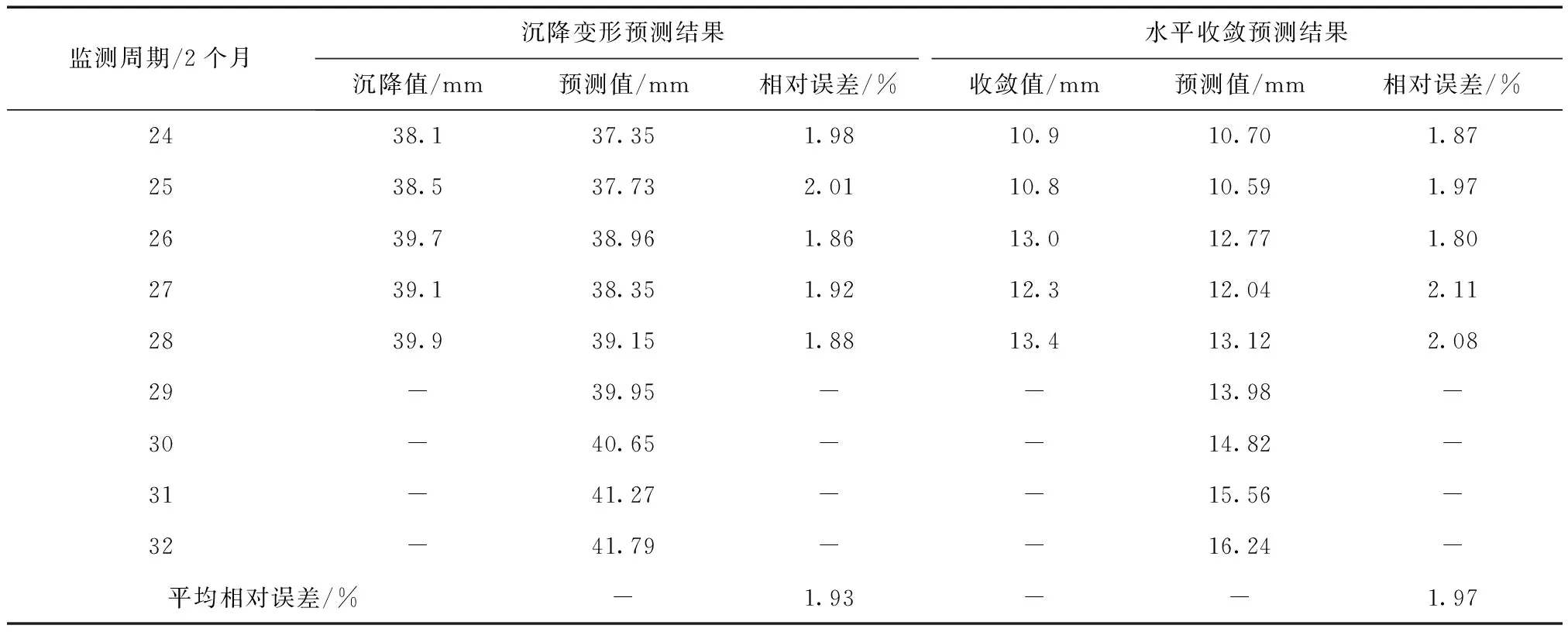
表5 STA211+90断面的最终预测结果

2.3 可靠性验证分析

按照文中研究思路，可靠性验证过程包含两个步骤，具体详述如下：

1)不同预测模型的对比验证。通过变形预测统计，得到文中预测模型、BP神经网络模型和GM(1,1)模型的预测结果如表6所示。据表6，3类模型的预测效果存在一定差异，在预测精度方面，文中预测模型具有相对最小的平均相对误差值，而在训练速度方面，文中预测模型也具有相对最短的训练时间，其次是BP神经网络和GM(1,1)模型，充分验证了文中预测思路相较于两类传统模型具有显著的优越性，验证文中预测思路的可靠性。

表6 不同预测模型的特征参数统计

2)变形趋势判断的验证分析。在隧道变形趋势判断过程中，可将分析流程再细分为两步，第一步是以所有样本进行M-K检验，以实现隧道变形趋势的整体判断；第二步则是分阶段进行M-K检验，共计划分为3个阶段，其中，阶段一为1～10周期样本，阶段二为1～20周期样本，阶段三为1～28周期样本。通过计算，得到隧道变形趋势的整体判断结果如表7所示。

据表7，沉降变形的Z值为1.948，趋势等级为1级，趋势程度弱显著；水平收敛的Z值为2.016，趋势等级为2级，趋势程度为显著；两者的发展趋势均呈增加趋势，但趋势等级相对较小。

表7 隧道变形的整体判断结果

同时，再进行分阶段趋势分析，结果见表8。据表8，随监测持续，两类监测项目的Z值虽大于0，但均呈减小趋势，说明随时间持续，隧道变形的趋势性趋于减弱，变形增加速率趋于减小，与前述预测结果一致，验证了外推预测结果的准确性。

表8 不同阶段的趋势判断结果

通过前述分析，得到嬉野隧道在后续运营期间的变形仍会进一步增加，但增加速率趋于减小，变形趋于稳定方向发展，即后期运营状况将会维持现状。

3 结 论

通过混沌-RF-SVM模型在嬉野隧道运营状况分析中的应用研究，主要得到如下结论：

1)通过模型构建过程中的递进优化处理，预测精度得以不断提高，验证了各类优化处理方法的有效性；同时，据混沌-RF-SVM模型的预测结果，得其预测精度相对较高，适用于运营隧道变形预测。

2)通过不同模型的预测效果对比，得出该文预测思路相较于两类传统模型具有显著的优越性，且趋势判断结果与预测结果较为一致，均得出嬉野隧道变形仍会进一步增加，但增加速率偏小，趋于稳定方向发展，将会维持现有运营状况。

3)限于篇幅，文中仅以一个监测断面为例，进行隧道运营状况分析，建议在条件允许前提下，可进一步对其余监测断面进行类似研究，以实现嬉野隧道运营状况的全面分析。