基于粒子群-最小二乘支持向量机模型的矿山爆破振动速度预测

何 理 刘易和 李琳娜 陈江伟 姚颖康 刘昌邦

(1.冶金工业过程系统科学湖北省重点实验室,湖北 武汉 430065;2.江汉大学爆破工程湖北省重点实验室,湖北 武汉 430056;3.中国建筑第七工程局有限公司,河南 郑州 450004;4.江汉大学精细爆破国家重点实验室,湖北 武汉 430056;5.武汉爆破有限公司,湖北 武汉 430056)

钻孔爆破是露天矿、隧道掘进和土建工程中最经济的破岩技术。超过80% ～85%的爆破能量通过地面耗散，并产生一些不良影响，如爆破地震效应、空气冲击波效应、爆破飞石等[1]。在这些不良影响中，爆破地震危害是矿岩开挖过程中最为显著的负面效应之一[2]。振动过大会对大坝、建筑物、基坑边坡和道路等结构造成严重破坏。因此，精确预测地面振动对于控制爆破引起的负面效应具有重要意义。质点峰值振动速度(Peak particle velocity，PPV)是评价地面诱发振动最常用的指标[3]。然而，由于爆破过程的复杂性及其与非均质、各向异性岩土体的非线性关系，获得一个封闭形式的数学模型极为困难。经验公式法[4-7]、BP神经网络及其改进算法[8-10]和数值模拟[11-13]等预测方法得到了众多学者们的认可。其中萨道夫斯基公式仅考虑最大单响药量和爆心距这两个参数，对复杂环境下的PPV预测误差较大;BP神经网络模型训练难度高[14]，需要大量训练样本完善模型以提高模型预测精度，不符合工程实际需要;数值模拟方法往往需要具备较强的数值计算技能，通常只能得到某种特定条件下具体的解，计算结果普适性不强。

近年来，随着计算机技术和机器学习方法的高速发展，逐渐出现了一些新的算法。作为一种新兴的机器学习算法，支持向量机(Support vector machine，SVM)具有较强的寻优能力，有助于解决爆破工程中样本少、影响参数多的实际问题[15-16]。LI等[17]和彭府华等[18]研究表明:两者分别提出的振动速度SVM预测模型具有可行性，且效果优于萨道夫斯基公式。岳中文等[19]结合主成分分析和遗传算法对SVM模型进行优化，优化后的模型收敛速度和预测精度均有所提升。KE等[20]将神经网络和支持向量回归模型混合编码形成杂交的智能模型，提高了对地面震动强度的预测精度。最小二乘支持向量机(Least squares support vector machine，LS-SVM)模型将SVM模型中的不等式约束变为等式约束，大幅降低了计算难度和复杂程度。但LS-SVM模型中的参数需要人为经验赋值，往往导致模型无法达到最优状态。因此需要一种进化算法对LS-SVM模型参数进行优化，通过全局搜索寻优的方式得到最佳的参数组合，从而克服关键参数依赖人为经验选取的不足。

本研究利用粒子群算法(Particle Swarm Optimization，PSO)确定LS-SVM模型最优参数组合，构建爆破振动速度预测的PSO-LSSVM模型，力求克服人为主观给定LS-SVM模型关键参数导致的预测误差较大的不足。首先设计开展露天矿山开挖爆破现场监测试验，采用灰色关联分析法，对实测PPV的各种影响因素进行敏感性分析，确定各种影响因素之间的主次关系;在此基础上，利用粒子群算法(PSO)局部寻优确定LS-SVM模型中正则化参数γ和核函数宽度系数σ的最佳参数组合;通过将PSO-LSSVM模型、LS-SVM模型、BP神经网络模型和萨道夫斯基公式的预测结果进行对比分析，结果反映出PSO-LSSVM模型的预测精度更高。研究成果可为复杂环境下的PPV预测提供新的思路。

1 PSO-LSSVM理论

支持向量机(SVM)是一类对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面[21]。LS-SVM算法是标准SVM算法的优化，主要优化特点是加入了等式约束，使得不等式约束求解变为解线性方程，从而大幅降低了算法的复杂性[22]。

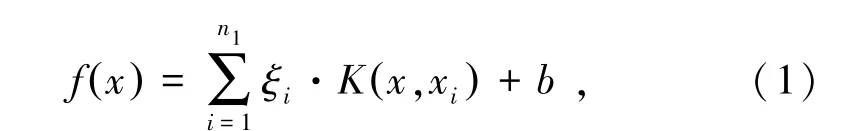
LS-SVM最终的优化函数为式中，ξi为拉格朗日乘子;K(x，xi)为核函数;b为偏置常数;n1为样本数据集。

本研究选取的核函数为高斯核函数，其表达式为

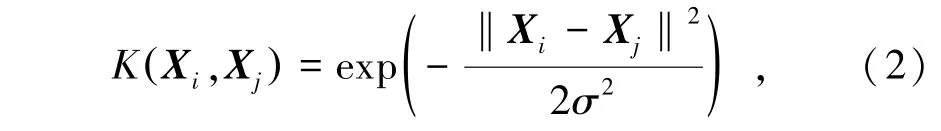
式中，Xi，Xj为n维向量中的两个样本;σ为高斯核函数的核宽度;‖·‖为向量的模。

研究人员一般通过经验选取LS-SVM模型的正则化参数γ和核函数宽度系数σ，得到的模型往往难以达到最优状态。因此本研究采用粒子群算法(PSO)迭代寻优LS-SVM模型的这两个参数，以提高模型的预测精度和收敛速度。PSO算法是由KENNEDY和EBERHART提出的一种进化计算算法[23]，其算法的灵感来自于生物体的社会行为，如鸟类聚集和鱼类成群。该算法由一群粒子组成，基于其最佳解来寻找最佳位置，包括最佳个人位置(pbest)和最佳全局位置(gbest)。在PSO算法中，粒子根据其位置和速度的运动过程公式为

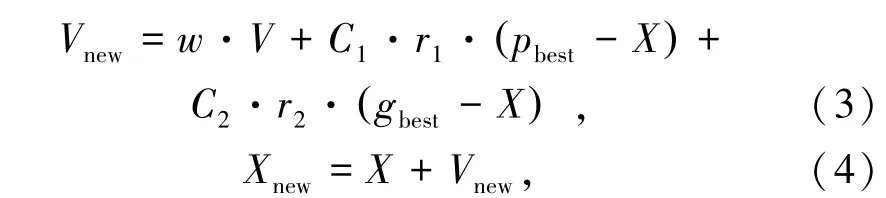
式中，C1和C2为学习因子;V和X分别表示当前粒子的速度和位置，Vnew和Xnew分别表示粒子的新速度和新位置;w为惯性权重系数;r1和r2是[0，1]区间内的随机数。

2 PPV影响因素的敏感性分析

2.1 工程概况

走马湖水系综合治理工程(机场配套项目)料源区位于鄂州市鄂城区沙窝乡黄山村，总占地面积2.33 km2。2号山为黄山西北侧山地，占地面积约0.26 km2，现地面高程为32～130 m。工程地理位置如图1所示。

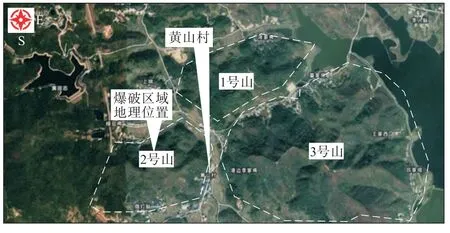
图1 工程地理位置示意Fig.1 Schematic of the geographical location of the engineering

由于2号山位于机场净空区内，根据设计要求，2号山开采范围线设置如图1所示，南侧山体由+105 m平台逐步放坡，最终开挖至+45 m高程，开采山体最高高程为+127 m，山体开采最高高度为82 m，总挖方量约436万m3，其中土方82.9 m3，石方353.1 m3。

在本爆破区范围内，大部分为砂岩，北部为花岗岩，南部为泥岩。根据爆区的地形、地质、岩性情况，结合工程工期及爆破渣块粒径挖装等要求，石方爆破施工主要采用深孔台阶松动爆破开挖，即各爆破作业区在运输道路开拓和台阶爆破作业平台创建后，沿山体外沿向中心区域从上至下后退式逐层开挖。设计多台阶深孔爆破，标准台阶高度为12 m，根据与周边保护民房铁路等保护目标的距离，采用数码电子雷管逐孔起爆网络，控制单响药量，减低爆破振动、飞石等有害效应。

2.2 PPV影响因素的灰色关联分析

灰色关联分析法的基本思路是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的灰色关联度就越大;反之，亦然[24-25]。该方法是通过计算系统特征变量数据序列之间的灰色关联度，建立灰色关联度矩阵，利用优势分析原则，得出各影响因素的顺序，最终确定出主要影响因素。

相关系数关联度的一般表达式为

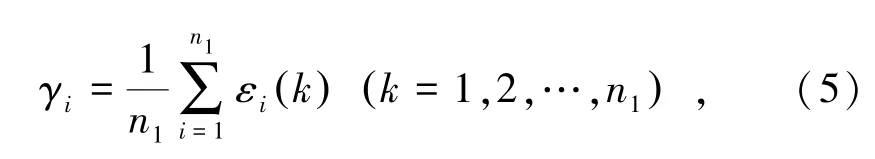
式中，γi为相关系数关联度;εi(k)为关联系数;k为样本集中第k个影响因素。

选取2号露天矿山实测的90组数据集(表1)进行分析，其中包括最大单响药量Q0、爆心距R、最小抵抗线W、孔距a、排距b、炮孔排数m、孔深h、炮孔数n、总药量Q和PPV等10个特征参数。

表1 实测数据统计结果Table 1 Statistical results of measured data

将表1数据代入式(5)得到每个参数与PPV值的特征参数影响因子关联度并进行了整理排序，结果见表2。

表2 特征参数影响因子关联度Table 2 Correlation degree of influence factors ofcharacteristic parameters

由表2可知:对PPV影响最大的特征参数是最大单响药量，炮孔数的影响最小。考虑到工程爆破现场测试成本及预测模型的计算效率等问题，文中选取最大单响药量Q0、爆心距R、最小抵抗线W、孔深h和总药量Q这5个特征参数作为模型的输入变量。

3 基于PSO的LS-SVM模型构建

根据式(1)至式(4)，本研究采用MATLAB仿真平台建立PSO-LSSVM模型，并对模型初始化参数进行设定，初始化参数取值见表3。

表3 初始化参数取值Table 3 Values of initialization parameters

将归一化处理后的90组数据集分为两组，前72组(即占总数据集比重为4/5)为模型的训练样本，对模型进行训练和学习，后18组(即总数据集的1/5)作为测试样本进行预测。得到PSO-LSSVM模型的适应度曲线如图2所示。

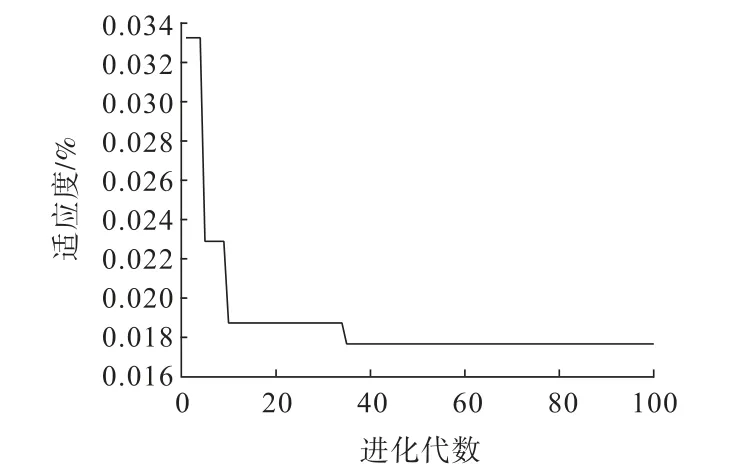
图2 PSO-LSSVM模型适应度曲线Fig.2 Adaptability curve of PSO-LSSVM model

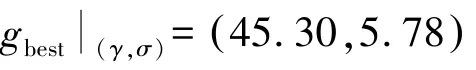
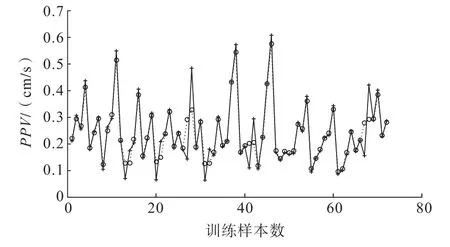
图3 PSO-LSSVM模型训练样本真实值与预测值对比Fig.3 Comparison between the real values and the predicted values of PSO-LSSVM model training samples

由图3可知:PSO-LSSVM模型的训练效果良好，统计得到训练样本的真实值与其预测值的均方根误差RMSE=0.05，相关系数R2=0.94，说明该模型回归拟合效果良好。

4 PSO-LSSVM模型预测结果分析

训练样本的回归拟合证明了PSO-LSSVM模型具有良好的学习能力，为了验证PSO-LSSVM模型同样具有良好的预测能力，通过输入18组测试样本数据进行预测，并分别与未优化的LS-SVM模型、BP神经网络模型和萨道夫斯基公式进行对比分析。4种模型对PPV的预测值与真实值的对比结果如图4所示。

由图4可知:PSO-LSSVM模型的预测值与真实值最为接近，效果明显优于未经优化的LS-SVM模型、BP神经网络模型和萨道夫斯基公式。

图4 不同模型的PPV预测结果对比Fig.4 Comparison of PPV prediction results of different models

为进一步量化对比各模型的预测精度，根据式(6)至式(9)分别计算拟合相关系数(R2)、均方根误差(RMSE)、平均相对误差(MRE)及纳什系数(NSE)等模型评价指标。

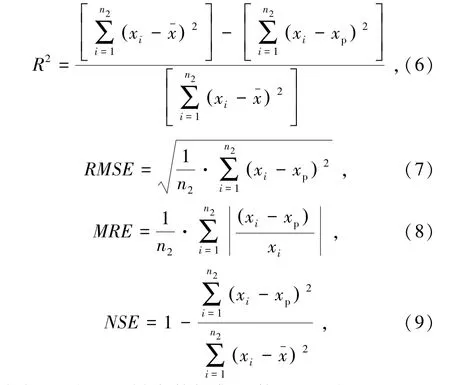
式中，n2为测试样本数据集的数目;xp为PPV预测值;xi为PPV的真实值;x-为PPV真实值的平均值。

为了避免数据集中存在特异值导致模型预测精度降低，使结果更具有可信度，本研究采用K折交叉验证(K-fold cross validation)法[26]对数据集和模型进行检验，K=5。具体评价步骤为:①将整个数据集分成均等5份;②依次取其中一份作为测试集，用其余4份作为训练集训练模型，计算每次模型预测结果的评价指标;③将5次预测得到的评价指标取平均值得到模型最终的评价指标。K折交叉验证后模型最终的各评价指标统计结果见表4。

由表4可知:BP神经网络模型对PPV进行预测时，R2为70.51%，RMSE为19.68%，NSE为33.99%，且模型的波动性最大，MRE为43.79%，该模型在本研究中预测效果较差。而萨道夫斯基公式的R2为79.42%，RMSE为16.03%，NSE为84.07%，MRE为38.76%，该公式在对预测的波动程度和准确性也不太理想，并不适用于该工程。未经优化的LS-SVM模型的R2为86.96%，RMSE为12.75%，相对于BP神经网络模型和萨道夫斯基公式，其预测精确度有较大提高，说明LS-SVM模型更适用于数据集样本较少的爆破工程物理量预测。经过PSO算法优化后的LSSVM模型的RMSE、MRE最小，模型的预测精度最高且波动性最小，R2、NSE最大，模型的拟合效果更好，能够更为精确地预测PPV。

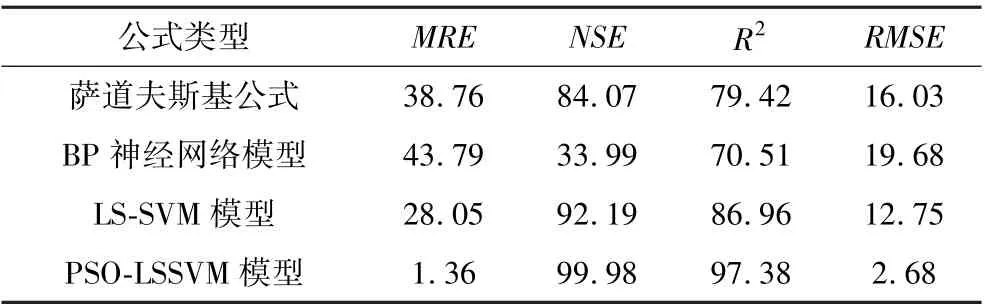
表4 模型评价指标Table 4 Evaluation indexes of the models%

5 结 论

通过灰色关联分析法对质点峰值振动速度(PPV)各影响因素进行敏感性分析，确定用于PPV预测的LS-SVM模型输入变量，并采用PSO算法确定模型正则化参数和核函数宽度系数，最后将PSOLSSVM模型预测结果与BP神经网络模型、LS-SVM模型及传统萨道夫斯基公式的预测结果进行了对比分析。主要取得以下结论:

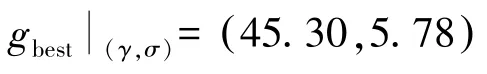
(2)PSO-LSSVM模型对PPV预测的R2为97.38%，RMSE为2.68%，MRE为1.36%，NSE为99.98%。与未经优化的LS-SVM模型、BP神经网络模型及传统萨道夫斯基公式相比，PSO-LSSVM模型具有更高的学习泛化能力及预测精度，在工程实践中用于PPV预测具有较强的适应性，是一种较为理想的人工智能预测方法。

(3)实际工程中，生产爆破现场存在海量的振动相关数据参数信息，现有的人工智能预测模型通常是基于少量或有限的监测数据统计分析而构建，且多是针对单一物理量进行预测，导致模型预测效果和适用性并非十分理想。未来亟需在行业内建立健全爆破振动监测规范及振动测试资料共享机制，充分利用人工智能、大数据与信息处理等先进技术，结合海量信息数据，构建爆破参数—爆破振动效应的联动数据库，力求为爆破工程技术人员提供潜在振动效应的查询、统计分析及智能预测服务。