液态CO2相变致裂器泄能头气孔压力研究

王 伟 李亚东 郑永香 尹 超 李朝博路小茜 周星宇

(1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;2.石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室,河北 石家庄 050043;3.石家庄铁道大学土木工程学院,河北 石家庄 050043;4.石家庄铁道大学河北省金属矿山安全高效开采技术创新中心,河北 石家庄 050043;5.河北省应急管理科学研究院,河北 石家庄 050051)

随着安全有序发展核电目标要求的提出，我国基本形成了包括核能在内的多轮驱动能源生产体系[1]。目前我国天然铀产量仅占需求量的25%[2-3]，长期依靠进口的现状严重限制了核电、核军工的有序发展。目前我国已探明的铀矿中，砂岩型铀矿占43%，原地浸出工艺(即“地浸”)是最有效、合理的开采方式[4-5]。地浸技术仅适用于渗透系数为0.5～10.0 m/d的高渗透性砂岩型铀矿[6-7]。然而，针对目前我国已探明的砂岩型铀矿普遍渗透性较低(渗透系数＜ 0.1 m/d)的现状，王伟等[8-9]提出了以炸药作为能量输入的低渗铀矿层“爆破增渗”物理改造方法，有效提高了低渗透砂岩型铀矿的渗透性。

随着技术的发展革新，传统炸药爆破的弊端逐渐显现，二氧化碳相变爆破在工程中得到了广泛应用[10]，众多学者对二氧化碳爆破原理及致裂效果进行了深入研究。二氧化碳爆破技术的基本原理为液态二氧化碳受热相变，短时间内体积急剧膨胀，由所产生的高压气体对周围介质进行爆破冲击[11]。相关试验研究表明，二氧化碳相变爆破的峰值压力和作用时间位于炸药爆破与水力压裂之间，且致裂效果良好[12]。夏祥等[13]通过开展岩体致裂和爆破试验，对振动速度传播和衰减规律进行了分析，发现二氧化碳致裂方式在中远区域的减振效果更显著，与传统炸药爆破方式相比，其爆破近区粉碎程度偏低，致裂效果更优。白鑫等[14]采用理论方法计算了液态二氧化碳相变致裂的影响半径，证明该技术可有效增加岩体损伤裂隙扩展。与此同时，部分学者对影响致裂效果的因素开展了相关研究。雷云[15]通过液态二氧化碳相变气爆压力试验平台及测试系统，对距爆口不同位置的压力—时间变化规律进行了研究，发现随着距离的增加，压力降低先快后慢，整体呈二次抛物线形式。XIA等[16]对二氧化碳爆破进行了一系列的探索性试验，通过综合分析对比液态二氧化碳充填量、加热材料用量以及定压剪切片厚度3个因素对爆破效果的影响，发现液态二氧化碳充填量对爆破效果影响最大，约为加热材料的231倍，剪切片太厚易导致爆破失败，管壁温度升高。ZHANG等[17]采用数值模拟和试验相结合的方式对裂隙扩展结果、试样破碎程度等进行了分析，认为剪切片强度、泄气孔数量和半径是影响爆破效果的关键因素。上述研究针对距离、充液量、剪切片厚度、泄气孔数量等爆破效果的影响因素进行了深入讨论，反映出二氧化碳爆破技术具有良好的致裂效果，有利于裂隙网络的形成扩展。然而，目前矿山开采等领域常用的工业化二氧化碳致裂器多由预切槽或单一泄气孔产生的优势流定向剥落周围煤岩体。该类致裂器应用于爆破生产中时，因其单一、少量的泄气孔，往往会产生较大压力，生成大主裂缝。煤层增渗领域所用的多孔释放管可以在一定程度上形成裂隙网络，而致裂器各气孔压力的变化趋势、压力差值等因素对所生成裂隙的均匀度有重要影响，故而有必要对其进行深入讨论。

爆破增渗需要通过致裂器产生大量连通的小裂隙，最终形成良好的裂隙网络。本研究在现有工业化生产的二氧化碳致裂器基础上，对致裂器泄能头进行多孔化设计，对泄能头上泄气孔之间的位置关系和孔径特征进行调整，以平衡、调节各气孔压力，从而达到对炮孔壁均匀加压进而产生大量微小裂隙、形成裂隙网络的目的。为实现上述目的，结合流体动力学相关理论，以RNGk-ε湍流模型为理论基础，分析泄能头腔体内的气体流动规律及压力分布特征;通过监测各气孔压力数据，讨论各气孔压力间的相关性、最大峰值、峰值差值等参数，得到了位置关系和孔径特征这两个因素对泄气孔压力的影响规律，为设计出适用于爆破增渗工况的“各气孔压力大且均匀”的致裂器提供理论参考。

1 模型构建

1.1 泄能头内气体流动模型

液态CO2相变产生的高压气体冲破剪切片射入泄能头内形成湍流，本研究采用湍流模型模拟泄能头腔体内气体的流动过程，并进一步监测各泄气孔压力。湍流模型主要有单方程S-A模型、双方程k-ε模型、五方程雷诺应力(RSM)模型、大涡模型(LES)等4种模型[18]，结合雷诺数等条件，选择相应的模型进行计算。

雷诺数是用来表征流体流动的无量纲数，雷诺数大小对选择湍流模型具有重要指导意义。其计算公式为

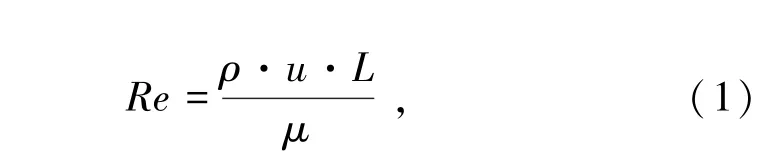
式中，Re为雷诺数;ρ为流体密度，气态CO2取1.787 8 kg/m3;u为流体流速，m/s;L为特征长度，取10-2m;μ为黏性系数，取1.37×10-5Pa·s。

将上述参数代入式(1)，结果大于4000，为高雷诺数。故本研究选取RNGk-ε湍流模型进行模拟计算。

为确保湍流模型计算的准确性，在湍动能k方程的基础上，引入湍动耗散率ε方程，形成k-ε双方程湍流模型。为适应高雷诺数流动问题，用重整化的数学方法对瞬时N-S方程进行推导，得到重整化k-ε模型(RNGk-ε模型)[18]，湍动能k和湍动耗散率ε由如下运输方程确定:

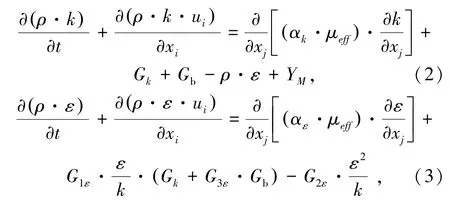
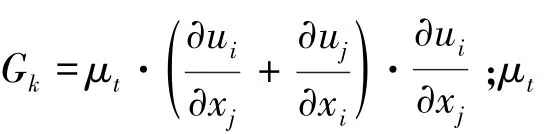
1.2 泄能头模拟方案及几何模型

1.2.1 模拟方案

本研究对传统二氧化碳致裂器泄能头进行多孔化设计，考虑两个变量:① 位置关系，根据泄气孔分布的几何位置，可分为对称式和交错式两种;② 孔径特征，根据同一泄能头上泄气孔直径是否一致，可分为均匀(5 mm)和非均匀(4～6 mm)两类。为充分对比分析各因素的影响程度，本研究依据控制变量法制定模拟方案，共设置4个基本类型，即均匀对称式分布、均匀交错式分布、非均匀对称式分布和非均匀交错式分布，见表1。

表1 泄能头模拟方案Table 1 Simulation schemes of energy discharge head

1.2.2 几何模型

根据表1所示模拟方案，本研究采用ICEM软件进行建模并进行网格划分。泄能头模型尺寸为100 mm×30 mm(长×宽)，入口设置在左侧首部居中位置，直径10 mm。依据泄气孔位置关系因素，上下壁面分别对称或交错地设置3组泄气孔;结合孔径特征因素，泄气孔直径设置为均匀式(均为5 mm)分布或非均匀式(分别为4、5、6 mm)分布，泄能头几何模型如图1所示。

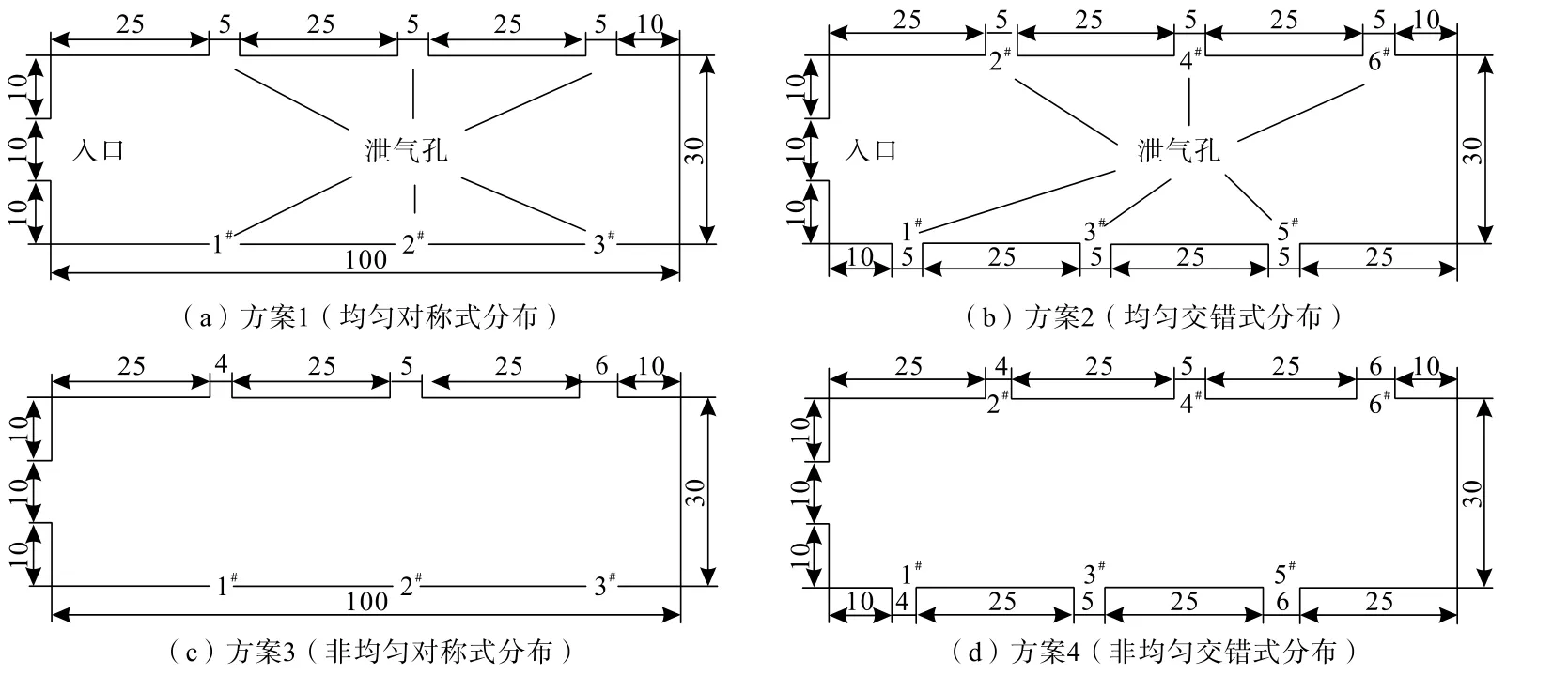
图1 泄能头几何模型(单位:mm)Fig.1 Geometric models of energy discharge head

泄气孔压力监测数据是分析位置关系和孔径特征对于气孔压力影响的关键性资料。本文的主要研究内容为高压气体的流动过程，无需考虑重力的影响。因此，对称式分布模型只对单侧泄气孔进行监测即可，即由左侧首部至右侧端部依次布设1#～3#测点;而交错式分布模型两侧泄气孔均进行监测，即由左侧首部至右侧端部依次布设1#～6#监测点，如图1所示。

2 泄能头仿真模拟

2.1 数学参数

为了对设计“各气孔压力大且均匀”的致裂器提供理论参考，本研究采用数值模拟方法，对所得各泄气孔的监测数据及压力—时间曲线进行对比分析。为提高数据分析的科学性、直观性，结合统计学理论引入了包括相关系数、最大峰值、峰值差值在内的3个数学参数。

相关系数方程(Correl函数)需具有两组数据即数组1、数组2，公式为

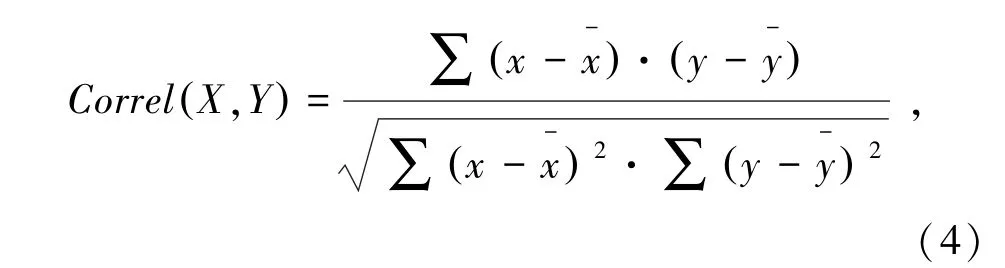
式中，X，Y分别为数组1和数组2的样本集合;，，分别为数组1和数组2的样本平均值。

相关系数表征各泄气孔压力数据随时间变化的一致性、相关性，数值越接近于1，各气孔压力越一致。各泄气孔压力数据两两组合计算相关系数，选取最大、最小相关系数，可有效避免出现同一泄能头上个别泄气孔之间压力数据高度一致而与其他泄气孔之间数据差异较大的情况。最大峰值表征同一泄能头各泄气孔所能达到的最大压力，数值越大压力越大。峰值差值定量表述各泄气孔之间的最大压差程度，数值越小各气孔压力越均匀。综上所述，相关系数越接近于1，峰值越高，差值越小，则可认定为越符合“各气孔压力大且均匀”的要求。

2.2 压力监测数据分析

根据表1所示的泄能头模型方案进行仿真计算，并对各监测点数据进行了包括相关系数、最大峰值、峰值差值在内的统计学分析，结果见表2。

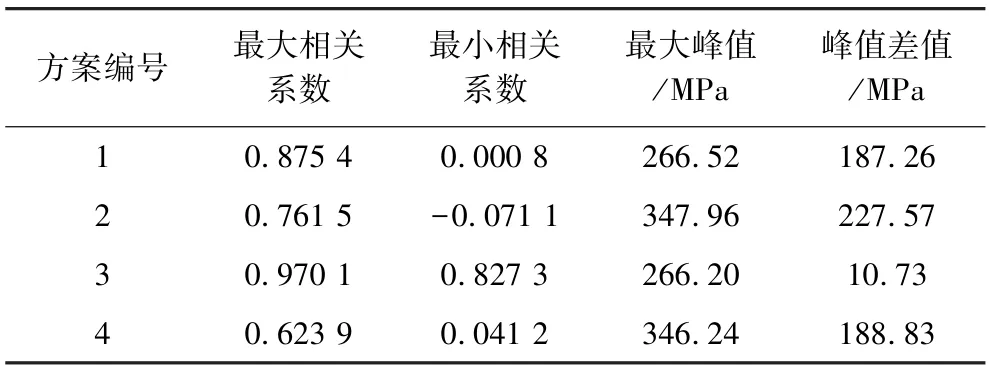
表2 泄能头气孔压力分析结果Table 2 Analysis results of vent pressure of energy discharge head

由表1可知:模拟1和模拟3(对称式分布)相关系数较大，尤其是模拟3，其各组监测数据间相关系数最小为0.827 3＞0.8，呈高度相关;最大可至0.970 1，几近于完全相关;且其泄气孔最大峰值达266.20 MPa，各泄气孔峰值差值仅为10.73 MPa。模拟2和模拟4(交错式分布)最大峰值较大，但其峰值差值较大。

2.3 腔内气体流动规律

对模拟过程中泄能头内空气和气态CO2的体积分数进行监测可知，腔内流体运动过程基本规律可以表述为:高速高压气体由左侧首部射入泄能头腔体，经右侧端部壁面反射回流，最后由上下壁面所设泄气孔释放。该过程中，壁面结构导致湍流、涡流等产生。计算初期压力波动较大，至0.5 ms时泄能头腔体内气体流动普遍达到相对稳定状态。

泄气孔呈对称式分布时产生对称涡流，增加能量耗散。一是因泄能头宽度有限，高压气体射流前端扩散不完全产生回旋涡流;二是端部壁面反射作用，产生涡流，另外由于上下壁面所设泄气孔的位置关系呈对称式分布，故其涡流也呈对称式，如图2(a)所示。但由于结构的对称性，其边界状况对腔内流体的扰动性整体较小，故尽管存在涡流，但腔体内气体流动整体保持稳定状态，上下壁面对应的气孔压力一致，有利于输出更加均匀稳定的压力。

泄气孔呈交错式分布时也产生涡流，其产生原因与对称式相似。但其边界条件不同，泄气孔的位置关系呈交错式，故产生非对称涡流，如图2(b)所示。本研究为高雷诺数气体(大于4 000)，惯性对流场的影响大于黏滞力，流体流动较不稳定，此种情况下流速的微小变化容易发展、增强，形成紊乱、不规则的紊流。因此边界对腔内流体的扰动性骤增，即湍流动能增大，致使压力波动较大，无法输出稳定压力。

图2 泄能头内气体流动对比Fig.2 Comparison of gas flow in energy discharge head

2.4 腔内气体压力分布特征

由腔内气体流动分析可知，高压气体首先冲击右侧端部壁面继而回流，此过程势必会在腔内气体压力分布上有所体现。为更好地探究泄气孔的位置关系和孔径特征对泄气孔压力的影响，需进一步分析泄能头腔体内的压力分布特征。

由泄能头腔体内压力云图(图3)可知，泄能头腔体内明显呈现出由右侧端部至左侧首部压力降低的特征，并且在计算初期，部分区域会出现压力负值现象。由于本研究雷诺数大于0.3，为可压缩流体，现引入气体压缩理论对压力特征进行分析，公式为

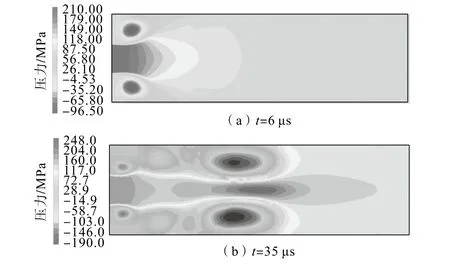
图3 泄能头腔体内压力云图Fig.3 Pressure nephogram of energy discharge head cavity

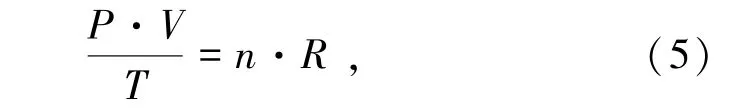
式中，P为压强，Pa;V为体积，m3;T为开尔文温度，K;n为物质的量，取0.5 mol;R为气体常量，取8.314 51 J/(mol·k)。

当雷诺数较大时，腔内气体微小的变化极易形成涡流、紊流，从而降低了气体的流动速度，如图4所示。射入腔体内的气体速度快，而紊流导致气体的释放速度较慢，故腔内CO2气体未能等量释放，即同等气体所占体积减小。CO2气体温度不变，物质的量以及R为常量，因此同等气体所占体积减小势必引起压力增大。又因为气体由端部回流至首部，沿途经过所设泄气孔释放，故呈现出由右侧端部至左侧首部压力降低的特征。

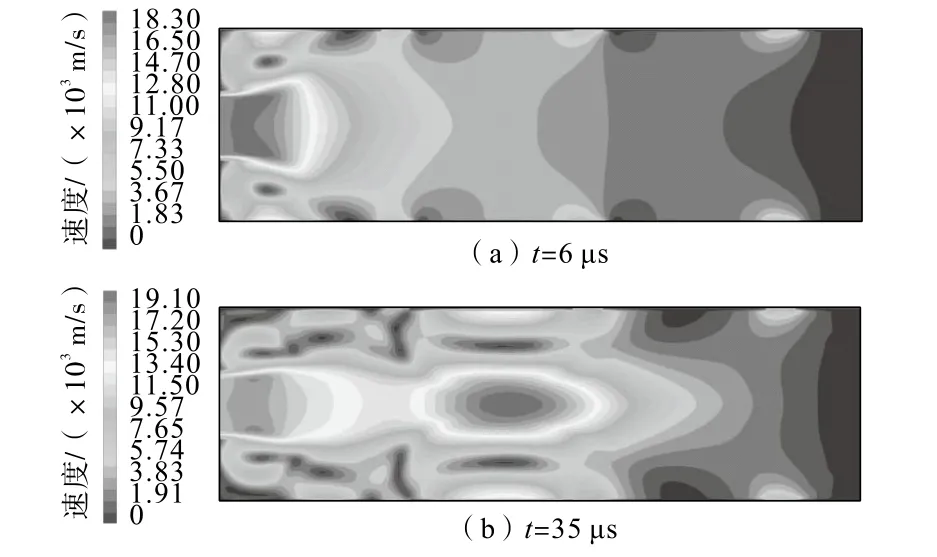
图4 泄能头腔体内速度云图Fig.4 Velocity nephogram of energy discharge head cavity

图3中涡流区域相对压力小于0，即呈现为负压现象。对泄气孔压力的大量监测数据以及压力—时间曲线进行分析发现，在大部分模拟试验的初始阶段以及个别试验的整个模拟过程中，存在负压现象。高压CO2气体喷射至泄能头腔体中，射流速度可达

1.91×104m/s，腔内气体速度分布如图4所示。依据射流负压理论，CO2气体由入口高速射入，周围空气被射流卷走，造成短暂的真空状态，继而临近空气被卷入，最终产生负压现象。同时研究表明，入射气体速度越大，形成的紊流传递给周围流体的动能越大、负压越低，但入口速度与负压的关系呈非线性[19-20]。

3 气孔压力影响因素分析

3.1 泄气孔位置关系对气孔压力的影响

在液态CO2相变爆破泄能头模拟试验中，泄气孔的位置关系是本研究考虑的主要影响因素之一。由上述泄能头腔体内的气体流动分析可知，泄气孔的位置关系导致边界条件变动，继而对腔体内气体的流动状况产生较大影响。本研究对方案3(非均匀对称式分布)和方案4(非均匀交错式分布)结果进行对比分析。压力监测点设置如图1所示，方案3设置3个监测点，方案4设置6个监测点，其压力—时间曲线如图5所示。

CO2相变爆破全过程持续时间较长，为减少计算量、并有效破岩，本研究选择其中压力为200 MPa左右的0.5～3.0 ms时间区间进行分析。由图5可知:方案3中各曲线走势一致，峰值范围为250～270 MPa，且3个测点达到峰值的时间基本一致;2#测点、3#测点的压力—时间曲线基本完全重合，1#测点与其他两组数据之间的差值维持在10 MPa左右，满足爆破增渗所需“各气孔压力大且均匀”的要求。方案4中，由于边界条件对流体的扰动性增加，形成极不规则的紊流，导致各曲线波动较大，无法输出持续稳定的压力。

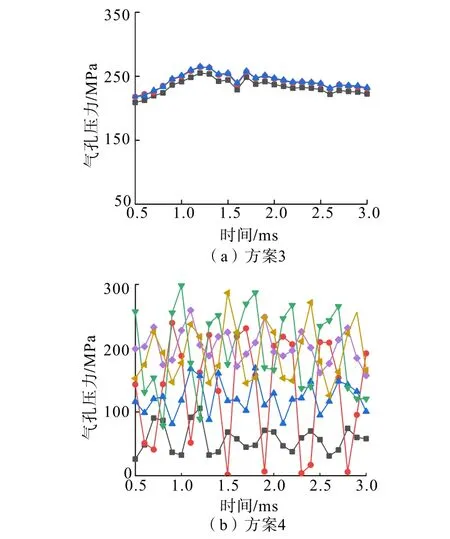
图5 不同位置关系下的压力—时间曲线对比Fig.5 Comparison of pressure-time curves under different position relationship

本研究分析表明:对称式气孔分布中，泄能头几何结构呈对称性，边界的规律性更强，对腔体内流体的扰动性更小。泄能头上各气孔压力稳定性相对更高，波动较小，压力—时间曲线具有很好的稳定连续性。交错式气孔分布中，微小的边界变化极大地提高了腔体内气体流动的紊乱程度，直观表现为气孔压力波动加剧。

综上所述，泄气孔位置关系对气孔压力的影响主要体现在压力输出的稳定性方面，对称式分布，气孔压力更加持续稳定;交错式分布，更易形成波动性脉冲气体。本研究认为:为形成均匀良好的几何裂隙网络，对称式气孔分布更适用于“爆破增渗”工况。

3.2 泄气孔孔径特征对气孔压力的影响

泄气孔孔径特征是本研究考虑的另一主要影响因素。依据孔径特征可划分为气孔直径由端部至首部降低的非均匀式分布和端部至首部直径相同的均匀式分布。通过分析泄气孔位置关系对气孔压力的影响可知:泄气孔呈对称式分布时气孔压力波动较小。为便于分析研究，选择方案1(均匀对称式分布)和方案3(非均匀对称式分布)来分析孔径特征对气孔压力的影响。压力监测点设置如图1所示，方案1和方案3均设置3个监测点，其压力—时间曲线如图6所示。

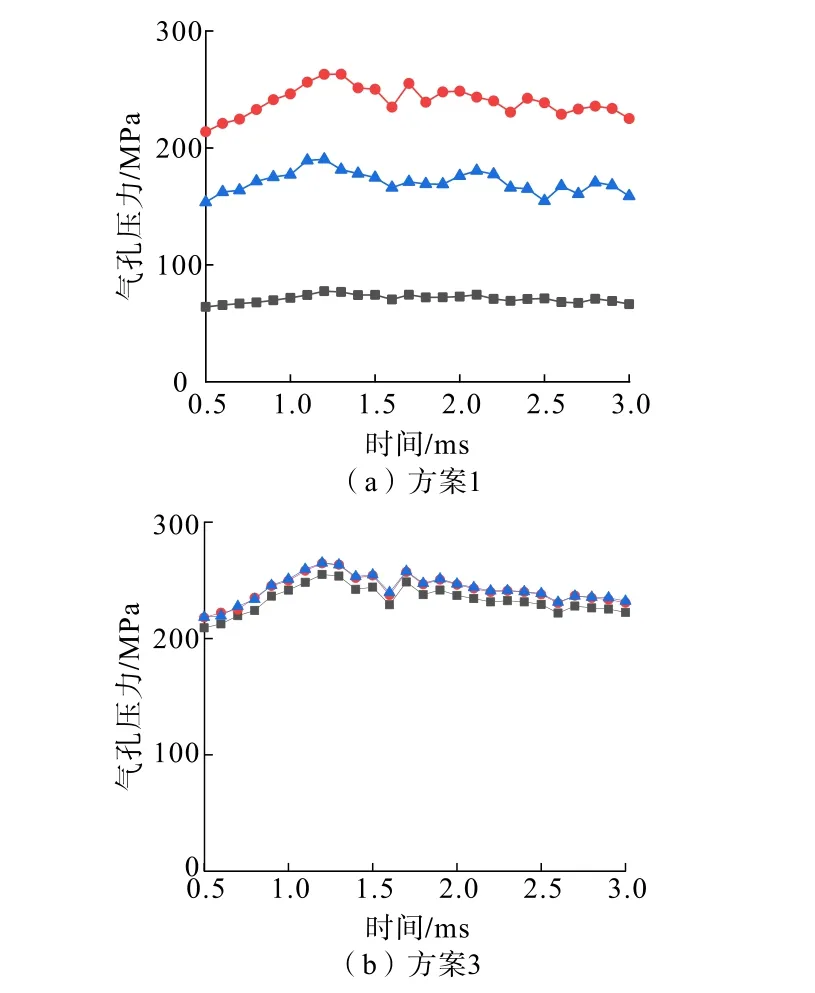
图6 不同孔径特征下的压力—时间曲线对比Fig.6 Comparison of pressure-time curves under different aperture characteristics

由图6可知:方案1中各曲线相对稳定，走势也趋向于一致。但2#测点压力围绕240 MPa波动;3#测点压力围绕165 MPa波动;1#测点压力围绕65 MPa波动，各气孔压力悬殊。结合模拟结果可知，方案1最大峰值压力为266.52 MPa，略高于方案3，但其最大差值达187.27 MPa，此种状况显然无法满足“压力均匀”的要求。而方案3的结果表明，其气孔间的压差较小，故其释放的压力更加均匀。

通过分析泄能头腔体内的压力分布特征可知，泄能头内压力呈现出由右侧端部至左侧首部逐渐降低的特征。泄气孔孔径特征呈均匀分布时，没有结合压力分布特征做出相应调整，导致各泄气孔差值较大，并不能很好地适用于爆破增渗工况。方案1中，高速气体冲击壁面产生回流，依次经过3#、2#、1#测点所在的气孔释放。均匀式的气孔布置致使压力大的端部区域气孔压力更大，压力小的首部区域气孔压力更小，最终形成巨大的压力差值。而模拟3结合腔内压力分布特征，3#、2#、1#测点所在的气孔直径依次减小，3处以扩大气孔直径的方式减小压力，相反，1处以缩小气孔直径的方式增大压力。通过一增一减的方式，平衡3组气孔压力，最终将各气孔压力差值控制在10 MPa左右。

综上所述，泄能头腔体内表现出由端部至首部压力降低的分布特征。孔径特征呈非均匀式分布时与压力分布特征相契合，故各气孔压力值近似，可提高裂隙均匀度，适合于爆破增渗工况;均匀式分布没有根据压力分布特征做出相应调整，致使各气孔之间压差较大，更适合于需要进行压差爆破的工况。

4 结 论

为降低泄气孔间的压差，获得更加均匀稳定的输出压力，采用数值模拟的方式进行分析，对所得泄气孔压力数据进行了统计学分析，研究了位置关系和孔径特征对泄气孔压力变化的影响规律。主要得到如下结论:

(1)泄能头腔体内压力呈现出由右侧端部至左侧首部降低的特征，因此将泄气孔直径设置为由端部至首部递减的非均匀式分布，可有效地平衡各泄气孔压力、降低压差;气体流动的雷诺数较大，故极小的边界改变都会引起腔体内气体流动的剧烈变化。因此，非均匀对称式分布，更易输出均匀持续稳定的压力。

(2)所研究的致裂器，其压力相对较小，在地应力更高的深层资源开采应用中可能会具有一定的局限性。因此需要综合考虑装药密度、加热装置与液态CO2的接触面积等因素，进一步研发威力更大的致裂器。