整车物流运输路径多目标优化

李永钦, 张庆年*, 杨杰

(1.武汉理工大学 交通学院, 湖北 武汉 430063；2.武汉理工大学 信息工程学院, 湖北 武汉 430070)

0 引言

整车物流网络路径优化问题是多式联运网络的一个重要研究内容,可以提供更好的运输方案,以达到合理化运输的目的。现有的运输路径模型构建大多数以总成本最小或总费用最低为目标,且多为以单任务流下的模型研究。张小龙等[1]以运输过程的费用成本、时间价值成本和环境成本为目标,引入混合时间窗约束,建立多目标多式联运模型。郑红星等[2]引入碳税机制,以总成本即运输成本、换装成本、延期成本与碳排放成本之和为目标,构建多式联运路径优化模型。Seo等[3]分析了中国重庆运输到欧洲鹿特丹的笔记本电脑案例,探索运输时间和运输成本之间的平衡。Resat等[4]以成本和时间为目标,建立了土耳其马尔马拉地区运输网络模型。具体到整车运输网络,部分学者开展了整车多式联运的综合研究。

胡元等[5]以成本最小化为目标,在满足时间约束的前提下,确定整车物流多式联运方案。Zeng等[6]考虑到运输成本、时间和运输能力约束方式,建立了汽车运输路径选择模型,使得运输总成本最低。杨自辉等[7]引入时间成本的思想,通过权重衔接的方法构建了物流运输路径优化的线性规划模型。刘弘超等[8]基于混合轴辐式理论,以运输网络成本最小为目标,建立整车物流多式联运网络优化模型,并以禁忌搜索算法求解。赵琨等[9]以中都物流有限公司为例,建立乘用车整车多式联运轴幅式网络,基于运输成本和时间成本,结合模糊综合评价法对枢纽点进行选择。姜彦宁等[10]考虑车辆和车辆分拨中心共享下的整车运输网络,以运输总成本最小为目标,建立0-1规划模型,并以遗传算法求解该问题。

一些学者也展开了对多运输任务下运输问题的研究。刘畅等[11]考虑了多产地和多品种的中欧笔记本运输路径问题,把时间价值成本纳入物流总成本中进行运输网络建模。谢楚楚等[12]以中欧班列为运输背景,构建了从中国到欧洲多个城市的考虑环境成本的路径优化模型。上述运输优化模型还是把运输时间、转换成本等视为常量,但是在运输过程中,运输过程的长短对于托运方来说至关重要,时间越是符合托运人的要求,该多式联运承运人在下次承运时被选中的概率就越大,因此承运人希望可以使托运人的满意度尽量高；在中转枢纽,伴随着到达时间的不同,季节等因素的不同,转换成本往往不尽相同。对于不确定环境下的整车多式联运问题,部分学者在考虑碳排放的情况下进行了研究。

梅梦婷[13]分别对时间窗约束下的单任务路径和运输能力限制的多任务路径进行了研究,并以三角模糊数表示运输时间和中转时间,通过机会约束规划转化模型。郑燕等[14]引入模糊数来表示不确定的运输时间和转运时间,考虑路段的拥挤度,在汽车公水联运网络中建立以整车物流运输费用、时间、碳排放为目标的0-1规划模型。刘虹等[15]在考虑客户满意度的基础上,建立了取货需求和送货需求随机性的多目标多行程车辆路径模型。蔡鉴明等[16]考虑碳税政策,以包含碳排放成本在内的系统总成本最小为目标,建立整车物流网络鲁棒优化模型。

目前的研究多是单任务流下的整车多式联运模型研究,关于多运输任务的研究较少。不确定环境下的多任务情况,在运输任务中普遍存在,承运人往往同时承运多个运输任务,其不确定的运输时间和中转费用对承运人来说不可忽视。基于上述不足,本文研究以区间表示的运输成本和运输时间、最低碳排放量为目标,引入转运节点的班期约束、货物运达时间窗约束和运输工具的运载能力约束,构建多运输任务下的整车多式联运运输模型。

1 问题描述与建模

1.1 问题描述

现有多批商品车,分别从不同的起运地送达不同的终点,中间经过若干节点,在运输时间和节点转换成本不确定的情况下,多式联运企业应该如何组织运输方案才能更好的满足客户需求和使自身的利益最大化。将路径优化问题转换为图论问题,构建这样一个图(V,E,N),V表示运输任务途径的各个网络节点,E表示各个节点之间存在的边及相关的权重,N表示存在的运输任务个数，因此,原问题可以转化为在图中寻找1条权重值之和最优的路径。本文采用多重点的方法建立图形,对于可达的节点来说,其不同的运输方法到达,那么该点就含有几个多重点。如图1所示,节点B可以由起点O经过公路运输和铁路运输到达,若以1表示公路运输,2表示铁路运输,3表示水路运输,那么节点B就可以转化为B1和B2表示的2个虚拟节点,如图2所示。这样虽然看起来节点的数目变多,但同时选定了运输路径和运输方式,使问题得到了进一步的简化。

图1 运输网络示意图

图2 运输网络分析图

1.2 模型参数及分析

① 模型假设。假设1：各运输中转节点均有充足的中转能力。假设2：在运输过程中,货流不可拆分。假设3：运输过程中不考虑其他不可抗力因素的影响,如台风、地震等自然灾害等。

③ 运输成本分析。

运输网络中的运输成本包括节点之间的运输成本、在节点进行运输方式转换的成本、在节点等待服务的成本和超过最佳送达时间的惩罚成本。

(1)

④ 运输时间分析。

运输时间包括节点之间的运输时间、中间节点的运输方式转换时间和在节点等待服务的时间。

(2)

⑤ 运输碳排放分析。

碳排放量包括运输过程中的碳排放和在节点进行运输方式转换的碳排放。

(3)

1.3 模型建立

(4)

(5)

(6)

(7)

(8)

(9)

(10)

tlijl-t3ikl≥0,

(11)

tl1gik=tlijk,

(12)

Z2h≤Fh,

(13)

(14)

上述约束式中:式(5)表示运输任务有固定的起点和终点；式(6)表示节点间只能选择一种运输方式,在一个节点只能转换一次；式(7)表示运输前后的连续性；式(8)表示节点之间运输不超过允许的最大运输能力；式(9)表示从起点流向终点；式(10)表示在节点j完成运输方式转换的时刻等于上一节点出发时刻、转换时间与路段运输时间之和；式(11)表示完成转换的时刻早于出发时刻；式(12)表示上一路段任务的完成时刻为下一路段的出发时刻；式(13)表示货物h的总运输时刻不超过额定时间；式(14)表示决策变量取值约束。

2 模型转换及求解方法

2.1 模型的线性化转换

由于模型的目标函数和约束条件均含有区间数,不能直接求解,借鉴于区间数的序关系≤CW(C和W分别指区间数的中点和半径值)和区间可能度对模型进行清晰化处理,将不确定性问题转化为确定性问题。

① 目标函数的处理。

对于式(1)中的max{*}部分,参照孙岩[17]和刘新旺[18]的方法进行线性的转化。

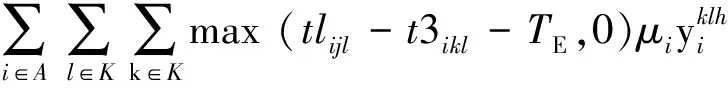
(15)

(16)

(17)

max(Z2h-Eh,0)μl可以转化为以下形式

Uhμl,

(18)

(19)

Uh≥0。

(20)

在λ和θ优化水平的基础上,式(1)和式(2)可以转换为

(21)

(22)

② 约束条件的转化。

式(10)可以转换为

(23)

(24)

(25)

式(15)可以转换为

(26)

经过转换后的线性化模型为:以式(21)、式(22)、式(3)为目标函数,添加式(16)、(17)、(19)、(20)为约束条件,式(12)、(15)以及转换后的式(24)、(25)、(26)为约束,其他约束条件不变。

2.2 求解算法设计

路径选择的过程涉及多个目标,本模型的求解是一个含有多个未知参数的多目标优化问题。非支配排序算法II(non-dominated sorted genetic algorithm-Ⅱ,NSGA-Ⅱ)通过计算不同个体之间的拥挤距离,划分层级,寻找最优非劣解,是解决多目标问题的好方法。由于存在交叉和变异操作,传统的NSGA-Ⅱ算法将最后一次迭代产生的种群作为非支配解,可能存在精英解丢失等问题,因此为避免精英解的丢失,本文以带全局存档的NSGA-Ⅱ多目标进化算法(NSGA-Ⅱ-archive)求解模型。带全局存档的NSGA-Ⅱ算法在迭代过程中将非支配解保存起来再进行交叉和变异操作,一方面可以保留好的解,提升计算效率,降低复杂度；另一方面可以克服精英解丢失的问题。

编码与解码设计:若采用0-1编码的方式表示各路径中的不同运输方式所表示的路线,如1-公-4,将给算法当中带来许多的约束,给算法的迭代进化带来许多的麻烦,使得求解最优集的时间变得很长,甚至难以得到最优解集,陷入局部最优，因此,本文采取基于优先度排序的间接编码[19]的方法。以一个6节点的简单例子来说明,如图3所示,存在1-2-4-6,1-2-5-6和1-3-5-6,1-3-4-6共4条路径,存在的可达点集合nodes为:nodes=[[],[2,3],[3,4],[4,5],[5,6],[6]]。Python中列表下标从0数起,表示节点0到节点5可以到达的节点的集合,因为节点0不存在,其可达点集合为空集。其染色体编码见表1,本例子起点为1,元素1的可达点为2和3,可以看到3的优先度大于2,因此第二个点选择3；同理元素3的可达点为4和5,5的优先度大于4,第三个点选择5,因此最终该染色体解码后的路径为1-3-5-6。通过解码可以得到符合路径约束的运输路径,但没有将时间窗约束考虑进来。对于时间窗的约束,将按照解码得到的路径依次计算到达各个节点的时间,如果到达时间符合时限要求,则按照对应的路径抵达下一个节点,否则需要进行等待,进行时间惩罚和费用惩罚的计算。

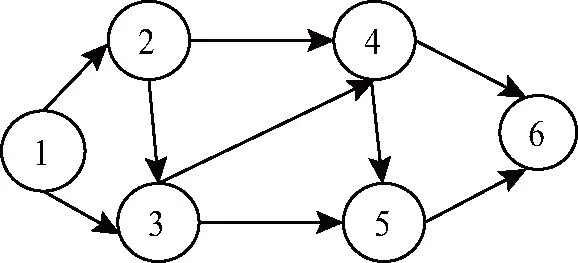
图3 运输路线示意图

表1 结点示意情况表

具体的步骤及方法如下:

步骤1:种群进化总代数为gen,进化代数i=0。

步骤2:初始化,随机生成若干初始种群。

步骤3:将初始种群进行非支配排序操作,对种群中的个体进行选择,并将非支配解存入文档。该操作的具体流程为:

① 找出种群中非支配解的个体,即ni=0的个体,将非支配解个体放入集合F1中。

② 对于F1中的每个个体,找出集合中每个个体所支配集合si,对si中的个体l,对nl进行减1,令nl=nl-1,若nl大小为0,则将此个体存放在集合H中。这是为了去掉已经挑选出的前沿中个体的影响,方便对剩下的个体进行排序。

③ 定义集合F1为第一层非支配集合,并为F1中每个个体标记相同的非支配序列。

④ 对集合H中的个体,按照以上步骤1、步骤2和步骤3操作,直至将所有个体分层。

⑤ 将非支配解存入文档。

步骤4:交叉操作,采用竞赛选择的策略实现个体的交叉。

步骤5:变异操作,随机选择个体进行变异。

步骤6:将交叉和变异产生的新个体与选择的最优个体进行组合,得到第一代种群。

步骤7:i=i+1,重复步骤4、5。

步骤8:父代种群和子代种群合并。

步骤9:快速非支配排序,对种群中的个体进行选择,将非支配解存入文档,计算个体之间的拥挤度,当2个随机个体处于同一非支配层级时,依据个体拥挤度判定个体孰优孰劣,个体拥挤度大的比个体拥挤度小的个体更优。个体拥挤度的计算公式见式(27):

Di=(fi+1,1-fi-1,1)+(fi-1,2-fi+1,2),

(27)

式中:Di表示第i个个体的拥堵度；fi+1,1为第i+1个个体的第一个子目标,以此类推。

步骤10:选择合适的个体组成新的父代种群。

步骤11:终止判断,若i达到算法最大迭代次数,对文档中的个体进行非支配排序,删除支配解,留下的则是非支配解,流程终止,否则i=i+1,并转到步骤7,具体流程见图4。

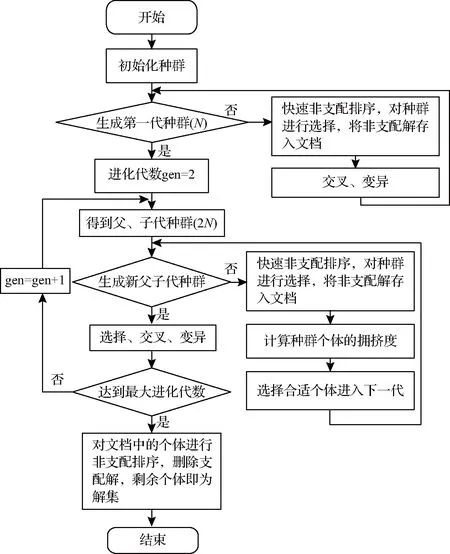
图4 算法流程图

2.3 模糊决策方法

经过算法求解得到的全局Pareto解集有很多个,根据决策者的需要可以采用模糊决策的方法从中选出最适合的最优解。根据解集提供的信息,可以定义各个子目标的满意度函数wi(x)为

(28)

式中:fi(x)为Pareto解集x的子目标函数值,fimax和fimin分别是Pareto解集x的子目标函数值中的最大值和最小值。对于每一个Pareto最优解集,其子目标的满意度都是确定值,为了更好的描述,对满意度进行模糊化的处理,以从解集中选出满足决策者偏好的满意解。

由式(28)可知,wi(x)∈[0,1]。采用三角形隶属度函数对满意度进行模糊描述,定义模糊规则为[极不重要 不重要 一般重要 比较重要 极其重要],如图5所示。最后,根据决策者需要对每一个目标选择一个重要度,就可以从最优解中筛选出满足决策者偏好的解。

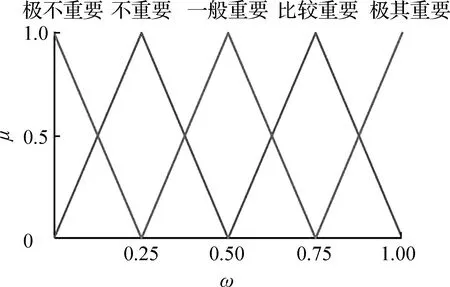
图5 三角形隶属度函数

3 案例分析

3.1 问题描述

一汽物流有限公司整车物流体系定位于集团整车物流系统的唯一载体,依托集团主机公司资源,构建起了高效的公、铁、水多式联运综合运输网络。文章以一汽物流有限公司整车物流为例进行分析,经中国汽车工业协会,达示数据查阅,收集得到宝来型汽车的需求量数据见表2。

表2 一汽-大众宝来型汽车的需求量数据

选择有代表性的3个分拨中心城市进行路径选择,所有城市节点包括起点长春,大连、天津、郑州3个分拨中心和上海、广州2个终点城市,城市节点序号编码见表3。

表3 城市排序表

表4 运输费用和碳排放因子

表5 单位转换成本和转换碳排放量因子

表6 节点服务时间窗

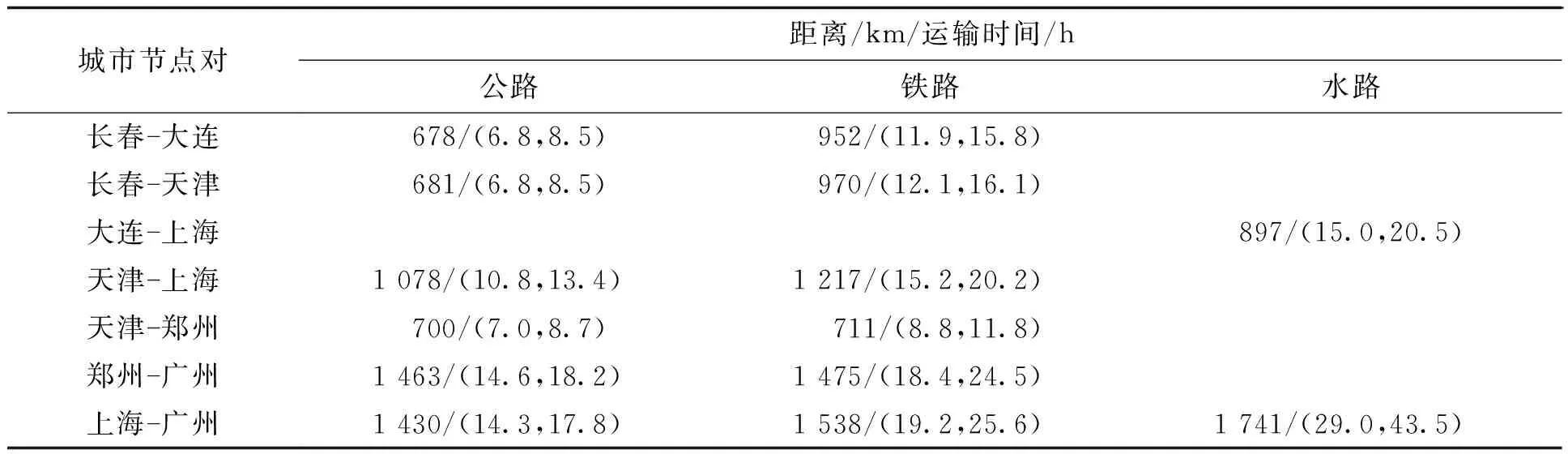
表7 运输距离和运输时间

3.2 结果分析

文章采用Python编程求解模型,对运输时间和转运费用的优化度设置为λ=θ=0.5,算法基本参数:种群大小为30,迭代次数为100,交叉算子为0.7,变异算子为0.01。分别以基础NSGA-Ⅱ,NSGA3算法和带全局存档的NSGA-Ⅱ进行求解,经多次测试运行,3个算法求解分别用时0.97、1.18、0.81 s,相比基础NSGA-Ⅱ,前者降低了11%的计算效率,后者提升了16%的计算效率,求解得到的非劣解集如图6-8所示。

图6 NSGA-Ⅱ最优解集

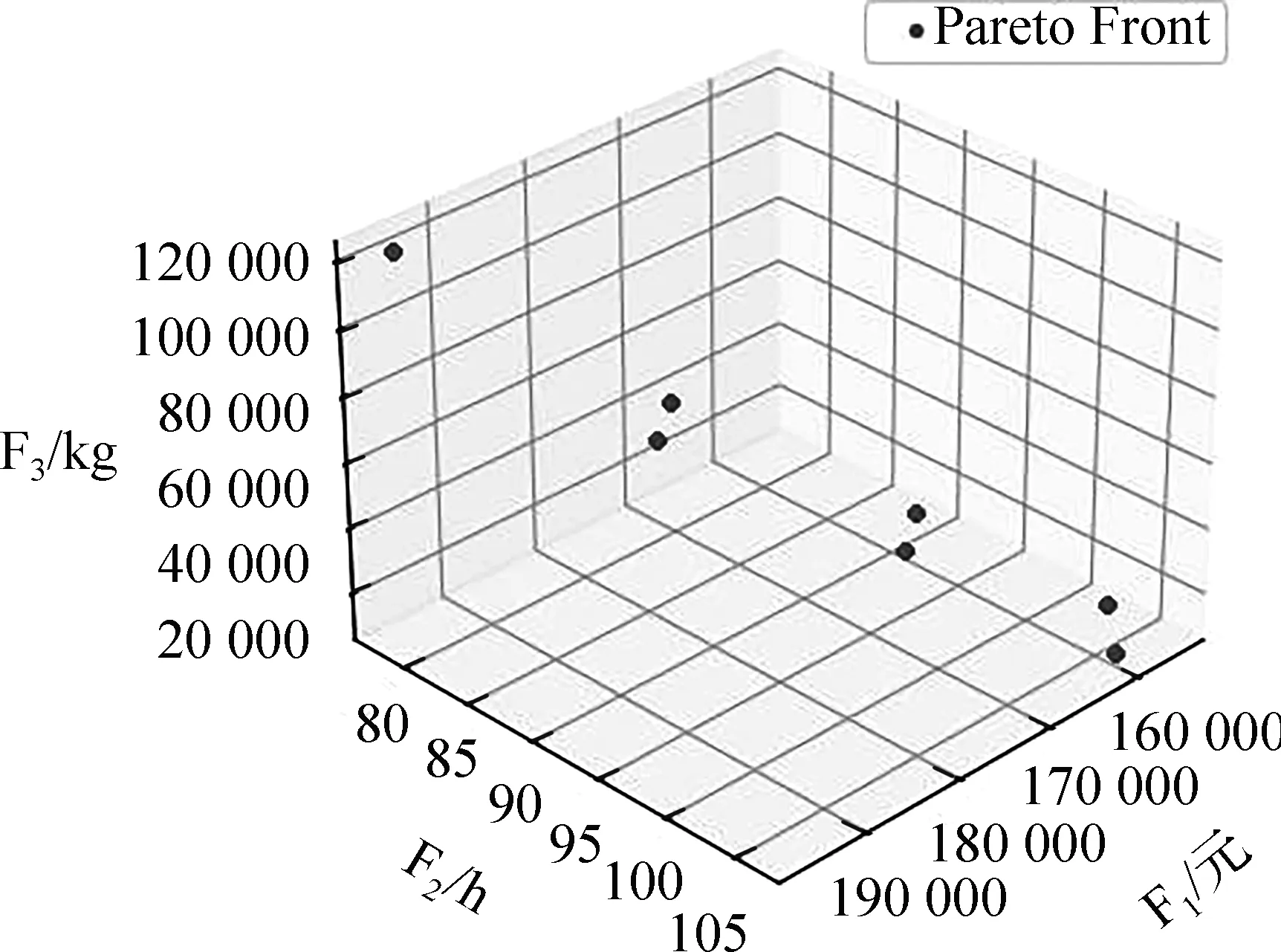
图7 NSGA3最优解集

图8 存档NSGA-Ⅱ最优解集

从图中可以看出,基础NSGA-Ⅱ和带全局存档的NSGA-Ⅱ这2个算法的求解结果相近,说明在本次求解中精英解没有发生丢失,但后者提升了16%计算效率,同时可以确保精英解的不丢失；NSGA3算法的求解结果略差于这2个算法的,说明NSGA3算法通过引入广泛分布参考点来维持种群的多样性方法对本例子的求解不适应,而且计算效率不如基础NSGA-Ⅱ算法的。表8给出了在综合考虑3个目标的情况下,以带全局存档的NSGA-Ⅱ算法编程计算得到的几组Pareto最优解,包括Python的输出结果及相应的解码路径,并计算各个子目标所对应的满意度,归类描述后见表9。

表8 最优非劣解集

表9 满意度

如果决策者更加注重运输费用,应该选择方案5,即1-3-10、1-5-7-12,运输路径为长春-铁路-大连-水路-上海、长春-铁路-天津-铁路-郑州-铁路-广州,最少费用为153 350.8元,耗时40.1、55.8 h,同时也是碳排放量最低的路径,碳排放量为18 483.0 kg。如果更加注重时间,应该选择方案6,即1-5-8、1-4-7-12,运输路径为长春-铁路-天津-公路-上海、长春-公路-天津-铁路-郑州-铁路-广州,耗时33.7、46.9 h,相应的运输费用和碳排放额较高。

4 结论

① 本文建立以区间参数表示的运输时间和转换成本下的多任务整车运输路线优化模型,在满足时间要求前提下,寻找综合考虑3个目标最优的路线方案,为决策者的路径选择提供支持。

② 以一汽汽车运输路径为例,在要求的混合时间窗要求下,通过多式联运方法,对比分析发现采用带全局存档的多目标遗传算法求解路径,在速度上优于基础NSGA-Ⅱ和NSGA3算法,还能避免迭代过程中的精英解丢失的问题。最后用模糊决策方法计算各个子目标的满意度,决策者可以根据对各个子目标的重要程度划分从中选择合适的运输路径方案。

③ 本文所运用的带全局存档的NSGA-Ⅱ优化算法能够有效处理多目标优化问题：一方面通过种群个体之间拥挤度的计算选择最优个体,来应对多个目标的问题;另一方面,通过在交叉和变异操作之前将精英个体进行存档,避免精英解的丢失和后续迭代的重复计算,提高求解效率。