两端带水平梯段钢梯梁挠度计算分析
2022-08-08周陈程俞海洪耿志光
周陈程,俞海洪,耿志光
(中石化上海工程有限公司,上海 200120)
在石油化工装置中,钢楼梯以其安装灵活、施工方便、重量轻、承载力高等优点,得到了广泛应用,常见的钢梯包括:设备框架平台钢梯、操作平台钢梯、屋面检修钢梯等。国内外对于钢楼梯的研究多集中在大跨度钢楼梯的振动舒适性方面[1-4],但是大跨度钢楼梯一般是出于对建筑美学和功能的要求,常用于公共建筑。对于工业建(构)筑物,大跨度钢楼梯极少。石油化工装置内钢梯梁一般采用槽钢,踏步板根据楼梯的防火要求而不同,常见的有两种做法:有耐火要求时,采用花纹钢板上铺一定厚度的混凝土;无耐火要求时,采用钢格栅。钢楼梯设计按GB 50017—2017《钢结构设计标准》[5]规定,需对钢梯梁的强度、稳定性以及挠度进行验算,其中对于强度和稳定性验算,可按钢梯梁的荷载分布求得最大弯矩以及考虑梯梁的侧向约束进行计算,但是对于钢梯梁的挠度计算,规范未给出明确的计算方法,只给出了限值。目前对于钢梯梁的挠度计算常参照混凝土的梁式楼梯计算方法,将楼梯荷载折算成均布水平投影荷载,按梯梁的水平跨度计算挠度,该计算方法对于采用钢格栅的楼梯来说显然不合适,钢格栅对梯梁竖向刚度基本没有贡献,斜段增加了梯梁的长度,其真实挠度会大于上述方法的计算值。本文针对此种情况,对两端带水平梯段钢梯梁挠度计算公式进行理论推导,并给出竖向挠度的简化计算公式,采用STAAD PRO建立简支钢梯梁模型,对理论公式和简化公式的计算结果进行验证,同时对不同支座类型的钢梯挠度进行计算分析,验证本文提出的钢梯梁挠度计算公式在实际工程中的适用性。
1 钢梯梁挠度计算公式推导
1.1 基本原理
梁挠度计算方法一般有两种[6]:结构力学变形体法[7]以及材料力学[8]挠度近似微分方程方法。虽然结构力学方法只要一次积分,但在求解时需对最大弯矩点是否在斜梯段上进行判别,分情况多次推导,而材料力学挠度近似微分方程由于只需根据弯矩函数(梯梁的弯矩函数可以以一个公式表述,无须分段)经过两次积分就可以得到梁的挠度曲线函数,故本文采用挠度近似微分方程进行计算。
受弯构件挠曲线近似微分方程如下:

对式(1)进行一次积分可以求得梁的转角函数:
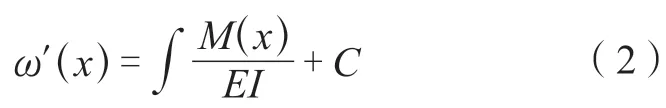
对式(2)再进行一次积分可以求得梁的挠度曲线函数:
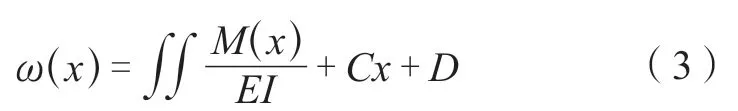
式中ω(x)——受弯构件的挠度曲线函数;
M(x)——构件截面弯矩函数;
EI——构件的截面刚度;
C,D—— 待定系数,根据边界条件和变形连续求得。
1.2 理论公式推导
楼梯荷载分布一般按均布水平投影考虑,如图1所示。将踏步板的水平投影荷载对其下斜梯梁段进行均分,得到等效的荷载布置图,如图2所示。
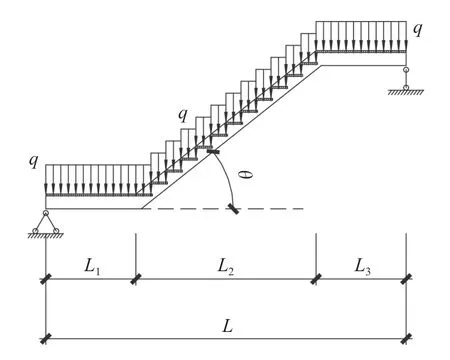
图1 均布水平投影荷载布置图Fig.1 Layout of horizontal projected loads arranged uniformly
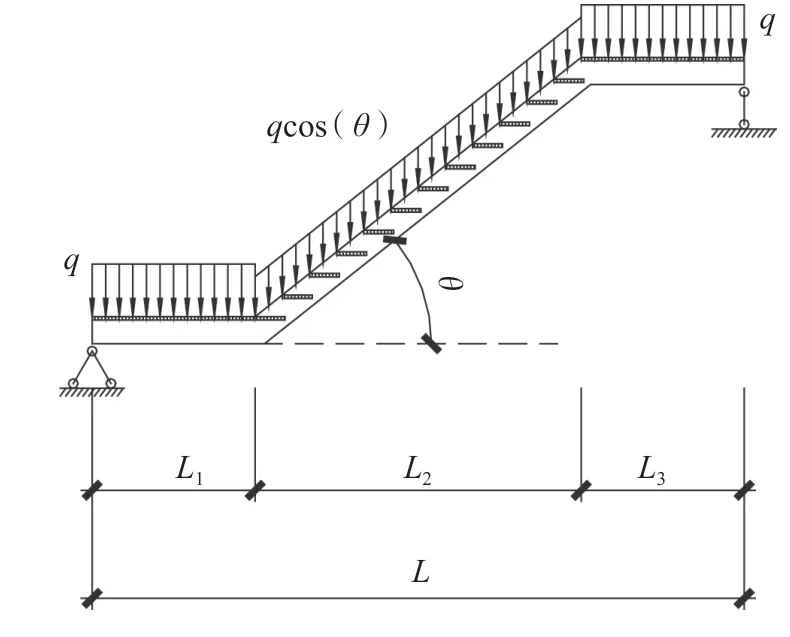
图2 等效荷载布置图Fig.2 Layout of equivalent loads
根据等效荷载布置图,求得梯梁的弯矩函数:
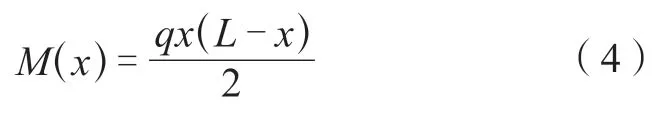
把式(4)带入式(1)后,进行一次积分求得梁的转角函数:
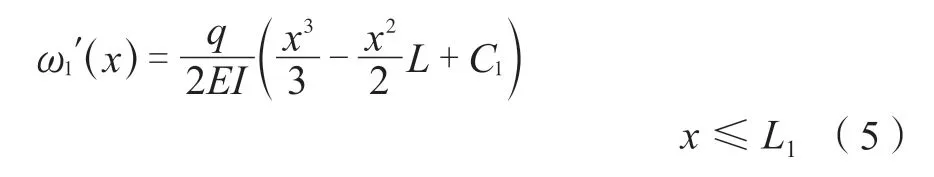
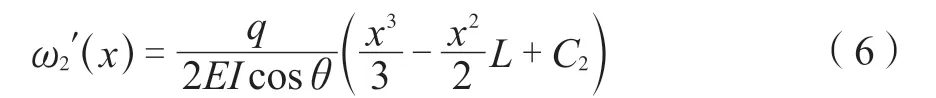
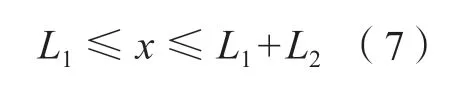
其中斜梁段的处理,如图3所示。
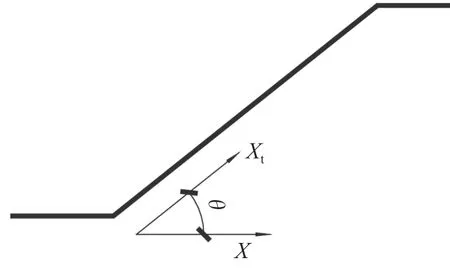
图3 斜梁处坐标轴Fig.3 Coordinate axes at the inclined beam
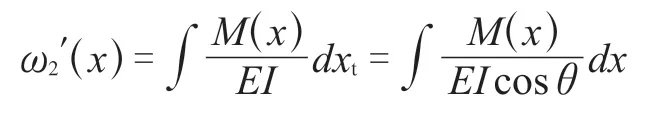
对式(5) ~ (7)积分,求得梁的挠度曲线函数:
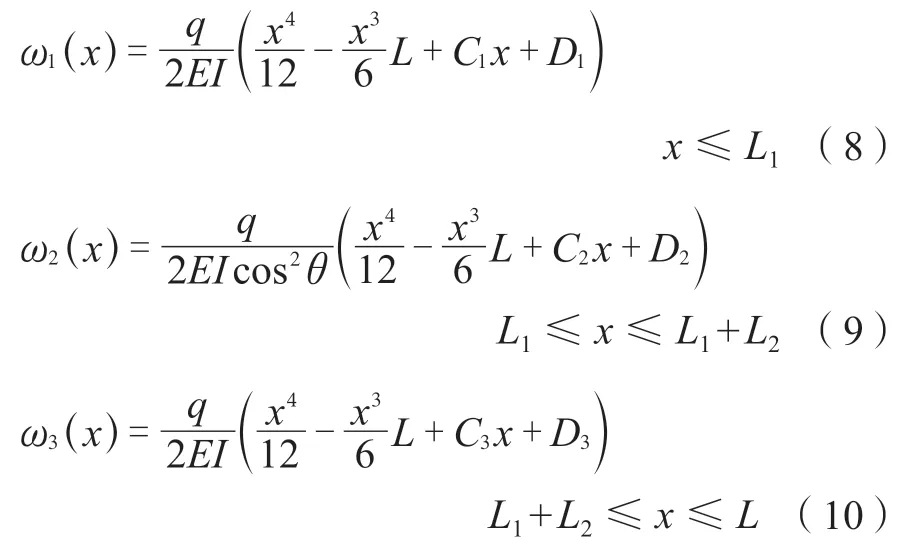
梁挠度是垂直于梁构件的变形,所以对于斜梯梁段必然存在水平和竖直两个方向挠度。对此分开讨论:
(a)竖向挠度
斜梯梁段竖向挠度与其总挠度存在如下关系:
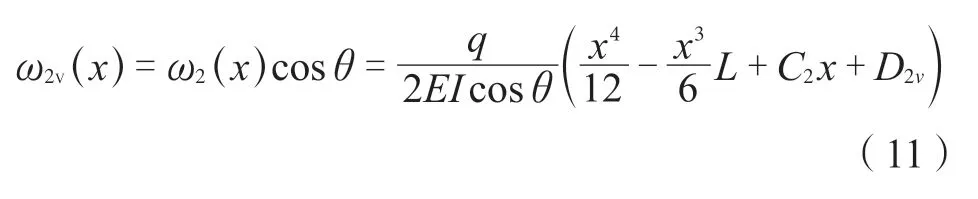
式中ω2v(x)——斜梁段的竖向挠度曲线函数。
根据边界条件、转角和竖向挠度的连续,即:
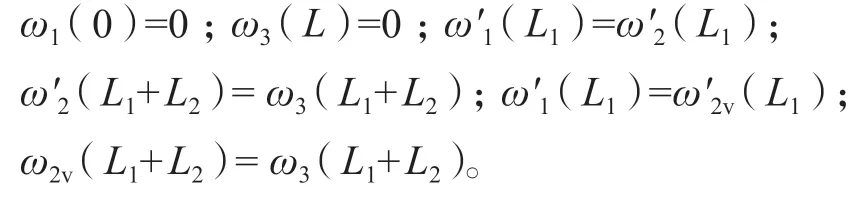
求得挠曲线函数中各未知参数,如下:
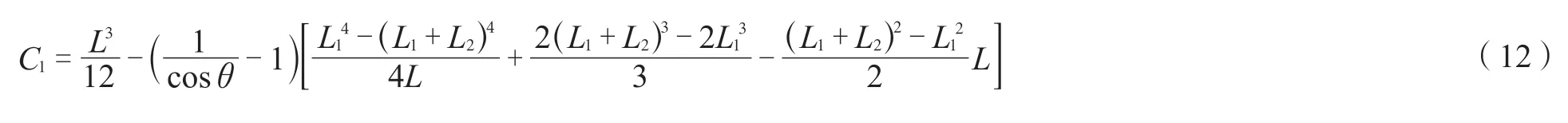
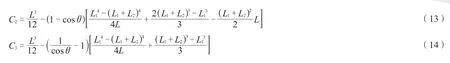

(b)水平向挠度
斜梯梁段水平向挠度与其总挠度存在如下关系:
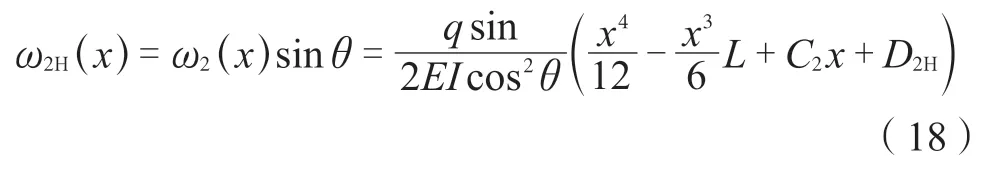
式中ω2H(x)——斜梁段的水平向挠度曲线函数。
根据边界条件即:
ω2H(L1)= 0;
求得斜梯梁段水平挠度曲线函数的未知参数,如下:

(c)极值点
由式(4)可以看出:对于简支钢梯梁,挠度二阶导数ω*(x)除两端外均大于0,所以在梯梁的有效范围内(除两端外)转角函数ω*(x)= 0的点即为挠度的极大值点。本文采用田红亮[7]给出的范盛金修正公式求解梯梁的转角函数式(5) ~ (7),一元三次方程有效解如下:
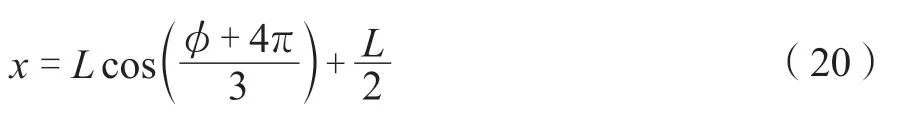
Ci见公式(12) ~ (14),单位:rad。
对于梯梁的竖向挠度,极值点的挠度就是最大竖向挠度。从梯梁的竖向挠度曲线可以看出,对于水平段较短的钢楼梯即L1<L/2且L3<L/2,此时最大的竖向挠度必然出现在斜梁段。但是对于一些特殊情况如L1>L/2或者L3>L/2时,发生最大竖向挠度的位置不再能简单判别是在斜梁段还是在水平段,需将C1~C3分别带入式(20)求出各自的极值点位置,再根据极值点位置是否在所计算梁段的范围内,判别所求得极值点位置是否合理,最终计算出准确的最大竖向挠度值。
对于梯梁的水平向挠度,由于上水平梯段水平挠度为定值,下水平梯段水平向挠度为0,所以梯梁的最大水平向挠度只能发生在斜梯梁段或上水平梯段。只需将C2带入式(20)求出极值点位置,再根据极值点位置是否在斜梯段的范围内,判别所求得极值点位置的合理性。最后把极值点挠度和上水平梯段的水平向挠度进行比较,即可得到梯梁的最大水平向挠度。
1.3 竖向挠度简化公式
从式(12) ~ (20)可以看出:钢梯梁的理论公式比较复杂,这对日常设计工作中快速验算存在较大难度。实际工程中,对于倾角不大的楼梯,水平向挠度一般比较小,不是主要的控制指标。故本节只对竖向挠度的理论公式进行简化。
从梯梁的弯矩函数可以看出,其与水平梁在均布荷载q作用下的弯矩函数完全一致。把斜梁段的转角函数、竖向挠度曲线函数和水平段相比,只差1/ cosθ,即可以把斜梁等效为一根长度为L2,刚度为EIcosθ的水平梁,如图4所示。
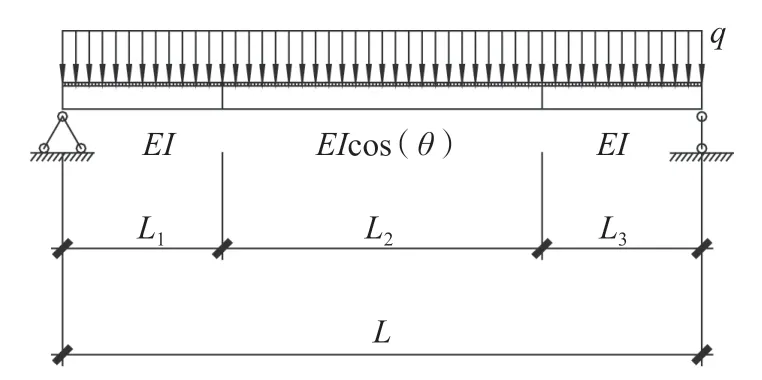
图4 等效水平梁Fig.4 Equivalent horizontal beam
经此,折梁问题转换成变刚度梁问题。从图4中可以看出,在均布荷载作用下,实际梁的最大挠度存在如下关系:

式中ω1——刚度EI的简支梁挠度,;
ω2——刚度EIcosθ的简支梁挠度,。
同时ωmax可以由ω1和ω2两个值进行表达,如下式:

α1、α2值分别与水平段、斜梁段占整根梁的比重有关,本文取值如下:
当L1≥L/2或L3≥L/2时:
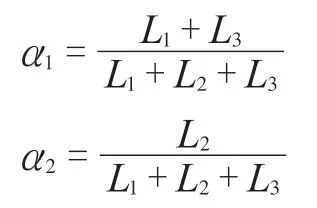
当L1<L/2或L3<L/2时:
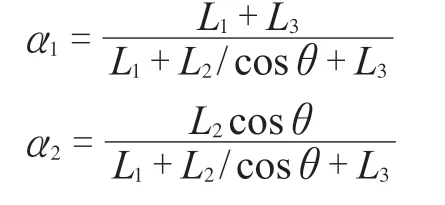
β为调整系数,经过试算,初步取值见下式:

2 计算模型验证
2.1 简支梯梁模型验证
为了验证理论公式的准确性,并对简化公式进行修正,采用STAAD PRO,建立不同跨度、倾角、水平段分布的简支梯梁计算模型,如图5所示。本文取荷载q= 1.5 kN/m;梯梁均选用[25a,惯性矩I= 3 359.1 cm4;梯梁跨度取常见的6 m、7.5 m、9 m;倾角取32°、38°、45°。梯梁最大竖向挠度和水平向挠度计算结果分别见表1和表2。

图5 简支梯梁模型Fig.5 Model of simply supported stair beam
从表1、表2中可以看出,理论公式在竖向挠度和水平向挠度上的计算结果与软件计算结果基本一致,误差都在2%以内,两者的差异主要在于软件计算时考虑了梯梁的轴向变形,而基于微分方程的理论公式忽略了轴向变形对挠度的影响。对比简化公式计算结果:水平段较小的梯梁竖向挠度与软件计算结果误差均小于2%,对于特殊的单水平梯段大于一半跨度的梯梁竖向挠度计算结果误差略大,但均在5%以内,能满足正常设计过程中的初步选型和验算, 值无需再修正。
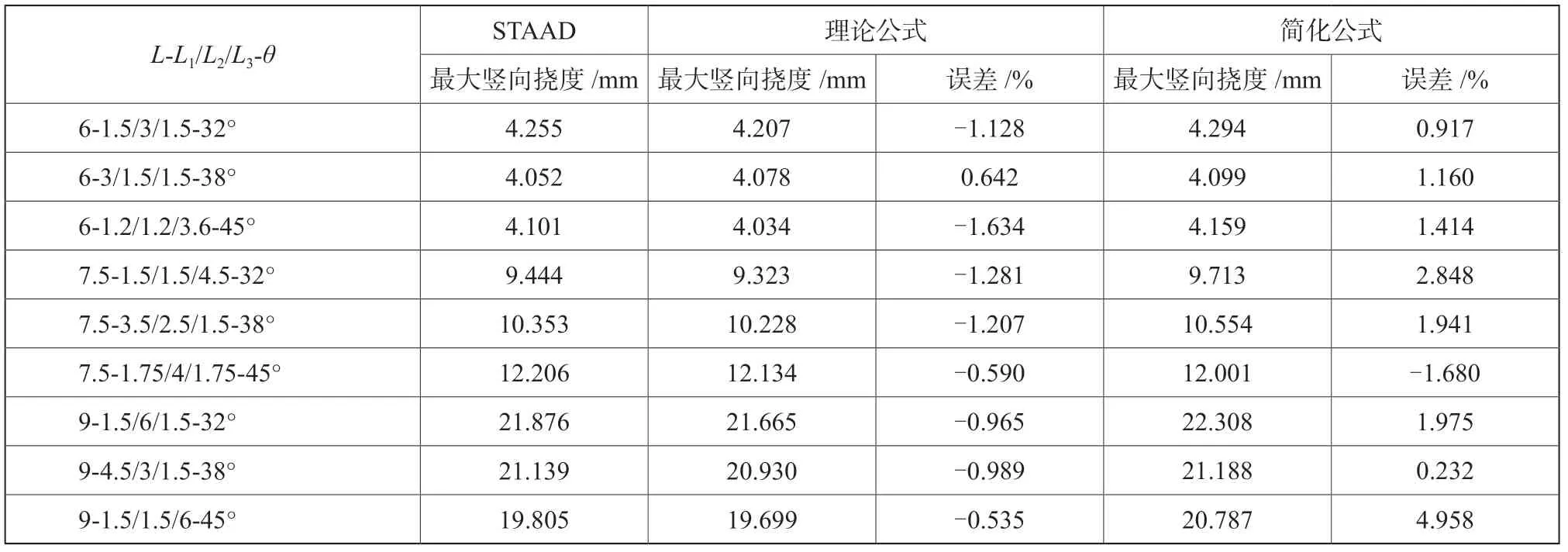
表1 竖向挠度计算结果对比Tab.1 Comparison of vertical deflection calculation results
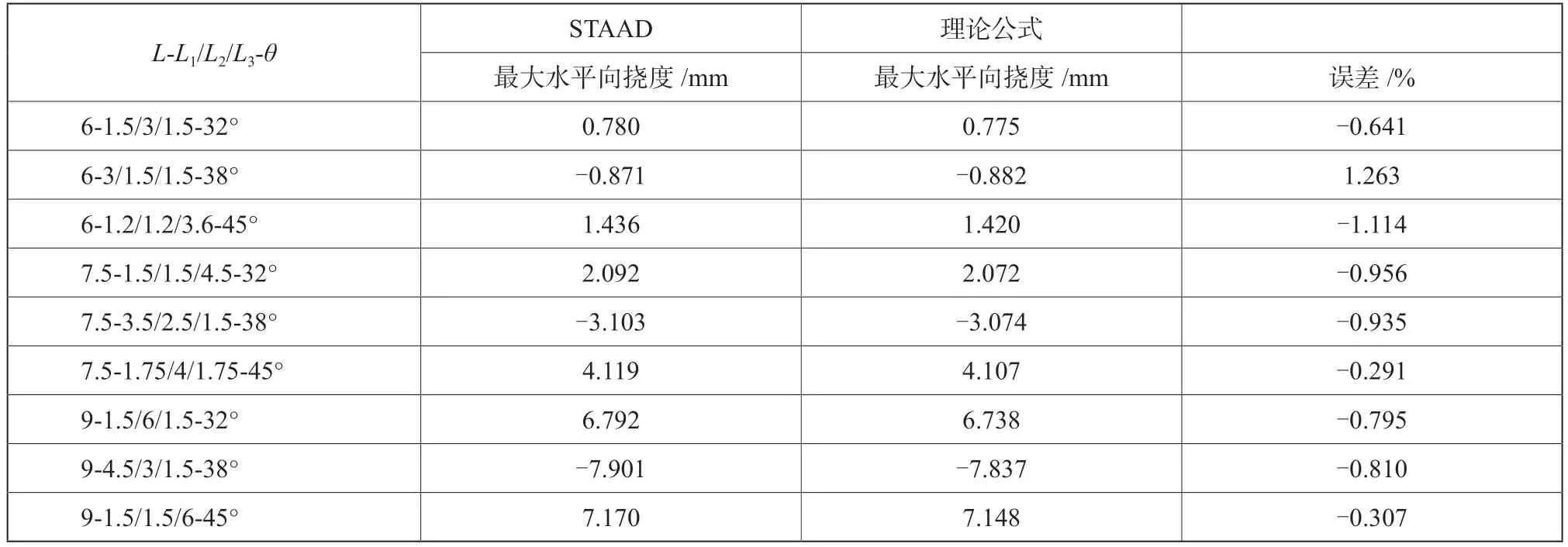
表2 水平向挠度计算结果对比Tab.2 Comparison of horizontal deflection calculation results
2.2 不同支座模型的验证
实际梯梁由于水平向受两端支座的约束,上下水平段会产生一定轴力,使梯梁的弯矩函数发生变化,具体的变化受支座的约束刚度影响,很难进行准确计算。本节采用STAAD PRO对设计过程中常见的钢梁支座和混凝土梁支座进行对比分析。模型中梯梁跨度6 m,跨度分布为1.2 m / 3.6 m / 1.2 m,梯梁倾角为45°,钢梁支座选为HN 250×125,混凝土梁支座选为250 mm×400 mm,梯梁规格和荷载同前文所述。钢梁支座和混凝土梁支座计算模型如图6所示。对外侧梁的计算结果进行统计,列于表3。
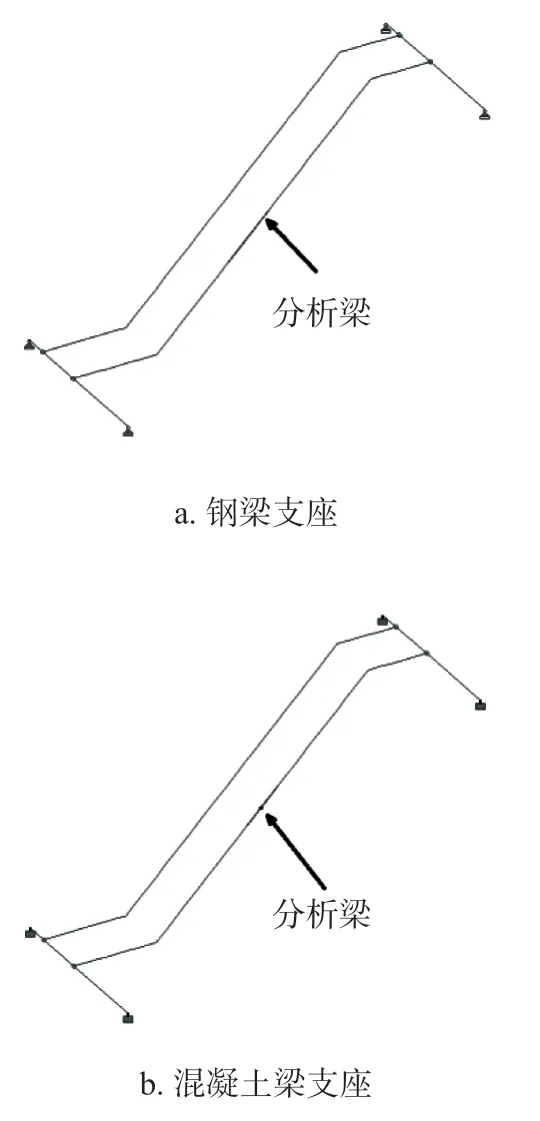
图6 不同支座类型计算模型Fig.6 Calculation models with different support types

表3 不同类型支座计算结果对比Tab.3 Comparison of calculation results with different support types
对比钢梁支座和混凝土梁支座:混凝土梁支座的梯梁最大竖向挠度比钢梁支座竖向挠度小8.34%,水平向挠度小7.04%,挠度最大值位置也更靠近上部水平梯段,接近0.25 m,这主要是因为混凝土梁支座两端刚接,它比钢梁支座的侧向刚度大很多,侧向约束使得水平梯段产生较大轴力,减小了梯梁下部梁支座的端反力,使得极值点往上水平段方向偏移。
对比不同支座的挠度极值与理论公式、简化公式计算结果:对于钢梁支座软件计算结果接近于标准简支梁,理论公式和简化公式计算结果与软件计算结果基本一致,其中理论公式的竖向挠度比软件计算结果小1.04%,简化公式比软件计算结果小1.53%,理论公式的水平向挠度小于软件计算结果1.36%;对于混凝土梁支座,理论公式和简化公式计算结果均略大于软件计算,其中理论公式竖向挠度比软件计算结果大7.97%,简化公式比软件计算结果大7.43%,理论公式的水平向挠度大于软件计算结果6.11%。
3 结论
(1)本文采用材料力学挠度近似微分方程方法推导出两端带水平梯段钢梯梁的竖向和水平向挠度曲线函数,基于范金盛修正公式求解一元三次方程的原理,给出挠度极值点的位置计算公式和计算方法。
(2)根据等效原理,把钢梯折梁等效为变刚度梁,提出钢梯梁最大竖向挠度的简化计算公式,并经过试算,给出调整系数。
(3)与标准简支钢梯梁的软件计算结果相比:理论公式求解的竖向挠度和水平向挠度误差都在2%以内;竖向挠度简化公式,对于水平段较小梯梁的计算结果误差也能控制在2%以内,对于单水平梯段大于一半跨度的梯梁误差在1% ~ 5%范围内。
(4)增加梯梁支座的侧向约束,能减小梯梁的挠度。
(5)理论公式和简化公式能很好地适用于钢梁支座的梯梁挠度计算。对于混凝土梁支座,理论公式和简化公式的计算结果偏大约5% ~ 10%,实际设计过程中可通过适当放宽规范限值或通过修正简化计算公式的β值来进行钢梯梁初步选型和验算。
