多频段环焦型椭圆波束天线优化设计

刘兴隆 杜彪 周建寨 解磊，2

（1. 中国电子科技集团公司第五十四研究所, 石家庄 050081；2. 西安电子科技大学 天线与微波技术重点实验室, 西安 710071）

引 言

随着移动卫星通信技术的快速发展，对车载、船载和机载动中通天线的低剖面、多频段、高效率和低旁瓣等性能提出越来越高的要求[1-4]. 针对小口径动中通天线不仅要求低轮廓，而且还提出了三个频段工作的应用需求. 为了实现多频共用馈源和网络良好的传输与辐射特性，整个馈源网络的结构复杂且体积较大. 这对小口径卡塞格伦型椭圆波束天线造成较大的馈源遮挡[5]，以至于天线效率降低、旁瓣升高和电压驻波比(voltage standing wave ratio,VSWR)恶化. 文献[6]针对双频段应用需求，提出一种混合型椭圆波束天线，在一定程度上减小了馈源的遮挡，但还是难以消除大馈源网络的遮挡. 环焦型椭圆波束天线具有较大的馈源安装空间，可以有效消除馈源的遮挡，但由于环焦天线的几何结构特性，赋形后的椭圆波束天线主反射面有奇异解，导致该方法设计的椭圆波束天线的轴比一般小于1.5∶1[7-8].文献[9-10]采用正交函数和非均匀有理B样条(nonuniform rational B-spline，NURBS)曲面对环焦椭圆波束天线进行了赋形优化设计，但其采用理想高斯馈源照射，未考虑实际馈源辐射方向图的不等化问题和馈源遮挡问题，且天线口径的椭圆轴比仅为1.55∶1.

基于物理光学(physical optics, PO)和物理绕射分析方法(physical theory of diffraction，PTD)，本文提出了一种环焦型椭圆波束天线的综合优化设计方法.该方法的特点是保留了环焦天线的优点，可容纳较大的馈源和网络；而且天线的主副反射面采用自由的控制点参数化表达，打破了传统的几何光学设计方法的能量守恒和等光程条件的约束，具有较大的设计自由度，可以优化出综合电性能优良、椭圆比较大的环焦型椭圆波束天线.

1 设计思路

首先，根据天线增益和轮廓需求，确定天线口径尺寸，赋形设计出环焦天线，再根据轮廓要求，将圆口径环焦天线切割成超椭圆轮廓环焦天线；其次，优化一维口面场分布曲线，使切割超椭圆赋形环焦天线达到较低的第一旁瓣和较高的效率；再次，将优化后的切割赋形环焦天线的三维主副反射面作为初始模型，用NURBS 曲面将其参数化，基于PO 和PTD快速仿真计算出天线辐射性能，并引入多目标优化算法，对天线效率和第一旁瓣等性能进行二次优化；最后，采用全波分析方法计算验证天线的传输与辐射性能，此时考虑馈源的宽带辐射特性、馈源与副面间的耦合以及副面支杆和馈源网络等结构的遮挡等.

该方法中的第一次优化为第二次的优化提供了较优的初始值，使得第二次的多参数多目标的优化成为可能，且能快速收敛.

2 设计方法

2.1 切割赋形环焦天线

2.2 切割赋形环焦天线的一次优化

切割赋形环焦天线由于俯仰面(短轴平面)能量漏失，导致天线效率降低和旁瓣升高. 为了优化天线效率和第一旁瓣，针对切割赋形环焦椭圆波束天线进行第一次优化设计，即采用三阶样条函数参数化一维口面场F(x)[12]，以天线效率和第一旁瓣为优化目标，优化切割赋形环焦天线，第一次优化设计流程框图如图2 所示. 该赋形设计方法中主副反射面之间满足几何光学原理，天线分析模型采用PO 和PTD 仿真计算天线辐射性能[13]，计算速度快，而且采用差分进化优化算法，其变量仅需6 个参数X=[p0,…,p2,…,p5]，所以本次优化需要较少的时间，便可以得到“最优解”. 经过种群数Np=30、最大优化代数量Gmax=150 的优化，得到最优解X=[0.263，0.982，0.615，0.775，0.354，0.751]，其表达的口面场曲线如图3所示.

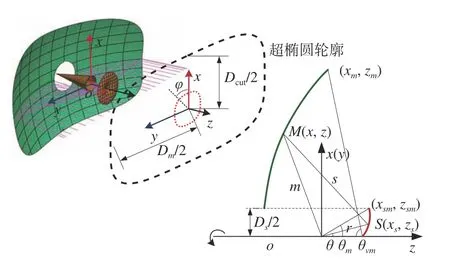
图1 切割环焦天线几何结构图Fig. 1 Geometry of the cutting ring-focus antenna

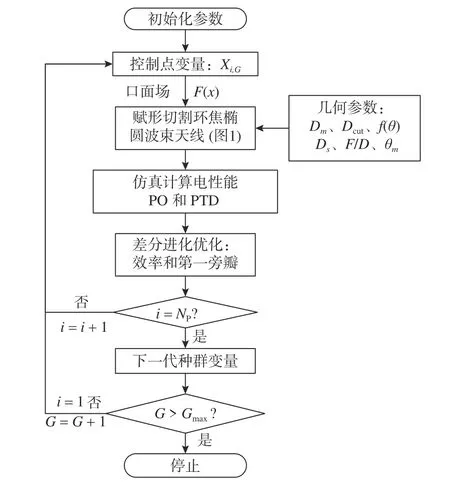
图2 切割赋形环焦天线的第一次优化设计流程Fig. 2 Block diagram of the 1st optimum design for the cutting shaped ring-focus antenna

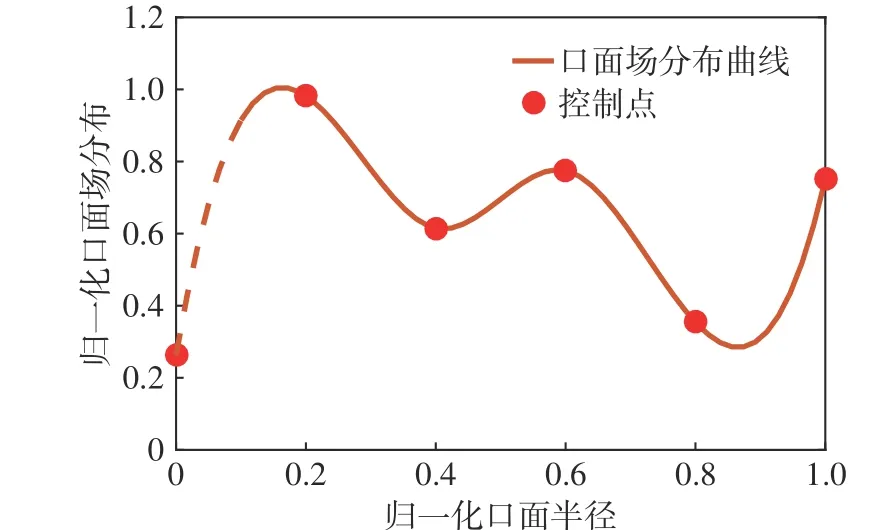
图3 第一次优化后的一维口面场Fig. 3 1-D aperture distribution after the 1st optimization

需要指出的是第一次优化设计是天线的第二次优化设计的基础，其优化出的“最优解”将会大大缩短后续多参数多目标天线优化的时间.

2.3 基于NURBS 曲面的椭圆波束天线多目标二次优化

一维优化切割赋形环焦天线可以通过优化口面场分布在一定程度上减少主反射面漏失，但受到几何关系的约束，主面的漏失还是不可忽略. 为了进一步提高优化的自由度，提出基于NURBS 曲面的环焦型椭圆波束天线的二次优化设计方法.

该方法的特点是天线的主副反射面用自由的控制点表达，具有较大的设计自由度，可以优化出更优的电性能. 同时由于该设计方法中天线主副反射面之间打破了等光程条件的约束，是按所需的多频段应用进行优化的，故其不再适用于任意频段的应用，只适用于本次优化的多频段应用.

2.3.1 NURBS 曲面参数化主副反射面

NURBS 曲面可用较少的控制点表达三维的天线主副反射面[14]. 相比于其他的正交函数，NURBS曲面的优化参数是控制点的坐标，不仅直观，而且不易出现特殊的敏感参数. 主副反射曲面均可用k×l次NURBS 曲面表示为

式中：ωi,j是控制顶点对应的权因子，决定NURBS 曲面与控制点的接近程度；Ni,k(x)和Nj,l(y)分别为x向k次和y向 l 次的规范B 样条基，它们分别由x向与y向的节点矢量按德布尔-考克斯递推公式决定；di,j为(n+1)×(m+1)个控制顶点，决定NURBS 主副反射曲面的形状，呈拓扑矩形阵列，形成一个控制网格.

由于椭圆波束天线是镜像对称的，只需(n+1)×(m+1)个控制点描述1/4 的反射面，将其镜像两次便可表示出整个主反射面或副反射面曲面，如图4(a)所示. 主反射面的控制点可采取均匀分布：

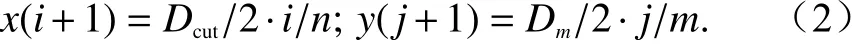
为有效地提高控制点对敏感区域的控制强度，减少控制点的数量，可对副反射面的控制点采取指数分布，即对中心区域加密：

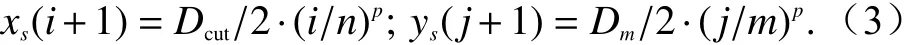
当取p=1.3，n=m=5 时，其控制点分布如图4(b)所示.

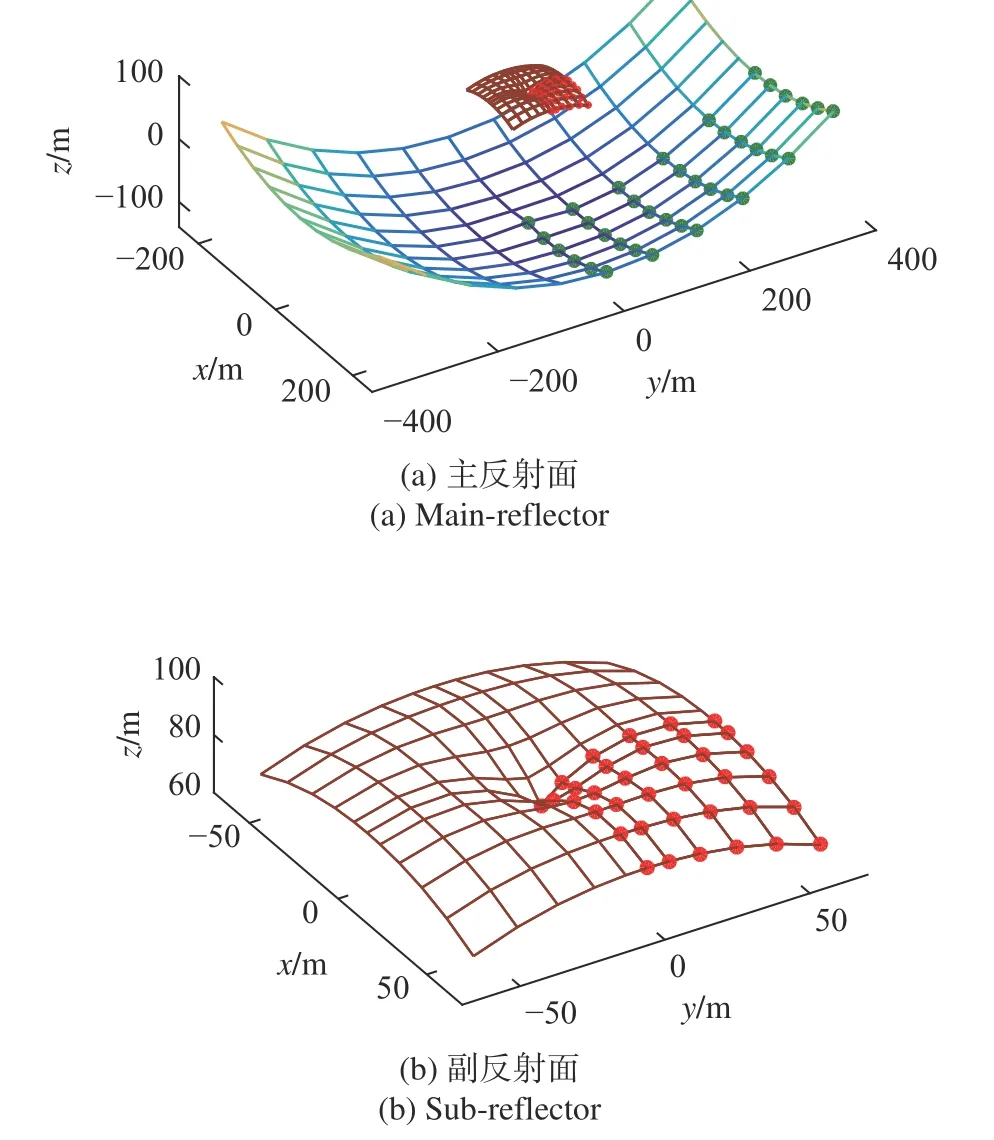
图4 NURBS 主副反射面及其控制点分布Fig. 4 NURBS surfaces of main-and sub-reflectors and distribution of the control points

2.3.2 双目标优化设计

在天线电气性能的综合优化中，天线口面效率和第一旁瓣是两个关键指标. 这两指标可以应用PO 和PTD 快速地仿真计算，该快速仿真计算方法使得多参数的三维曲面优化设计成为可能. 然而，选取合适的双目标权重系数，将其转化为单一目标的优化问题较为困难，且每次优化只能得到一个最优解.因此，本文引入多目标优化算法[11,15]，在优化后的Pareto最优解集合中，选出具有足够余量的最优解，结合全波仿真分析，优选出效率、旁瓣和驻波比等性能的综合最优解.

将最大化三个频段收发共NF=6 个中心频点的天线效率和最小化对应的第一旁瓣的优化问题转换为以下两个目标函数的最小化问题：

多目标排序采用快速非支配排序法，给每个个体分配前沿，并结合拥挤距离计算，对每一代种群个体进行排序. 其中高级别的前沿个体和拥挤距离较小的个体为较差的个体.

针对本文的双目标优化问题，采用多目标差分进化算法，优化得到Pareto 最优解集，综合选取出最优解，经过全波仿真验证后，即完成了第二次优化设计，整个设计流程如图5 所示. 优化参数的取值为：种群数量Np=60，差分尺度因子F=0.3，交叉因子C=0.5，最大优化代数Gmax=300.

图5 椭圆波束天线的第二次优化设计流程Fig. 5 Block diagram of second optimum design of elliptical beam antenna

3 设计案例和测试验证

天线的几何参数可以根据天线增益和效率的需求以及安装空间的约束条件确定，天线指标如表1所示. 确定的天线参数Dm=720 mm，Dcut=410 mm，Ds=120 mm，F/D=0.3，θm=37°，馈源照射电平-12 dB，超椭圆系数v=3.8. 其中超椭圆等效直径580 mm，比标准椭圆口径的面积增加了15%，更有利于实现天线高增益，可提高0.6 dB.

表1 天线参数Tab. 1 Antenna parameter

图6 为用均匀口面场赋形设计的切割环焦天线的模型、光路和方向图. 依据图3 所示的一维优化口面场，赋形设计的天线模型、光路和方向图如图7所示.

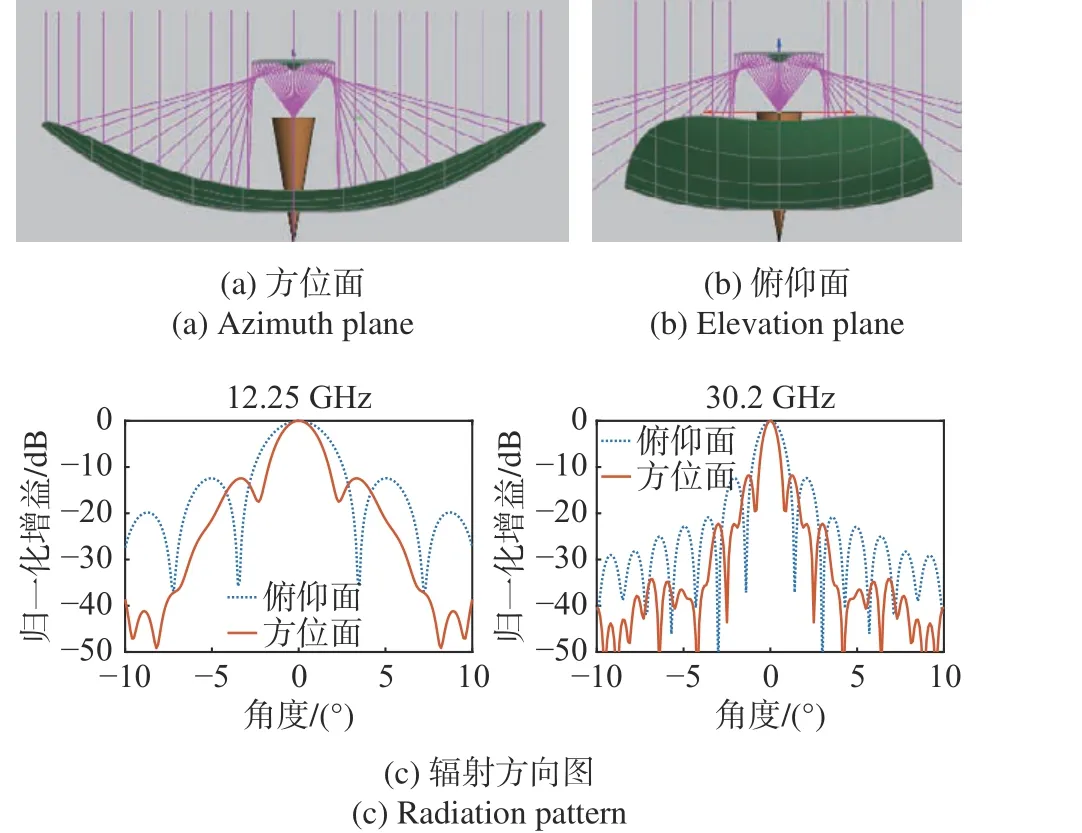
图6 均匀口面场赋形的天线模型、光路和辐射方向图Fig. 6 Shaped antenna model with the uniform aperture distribution and radiation patterns

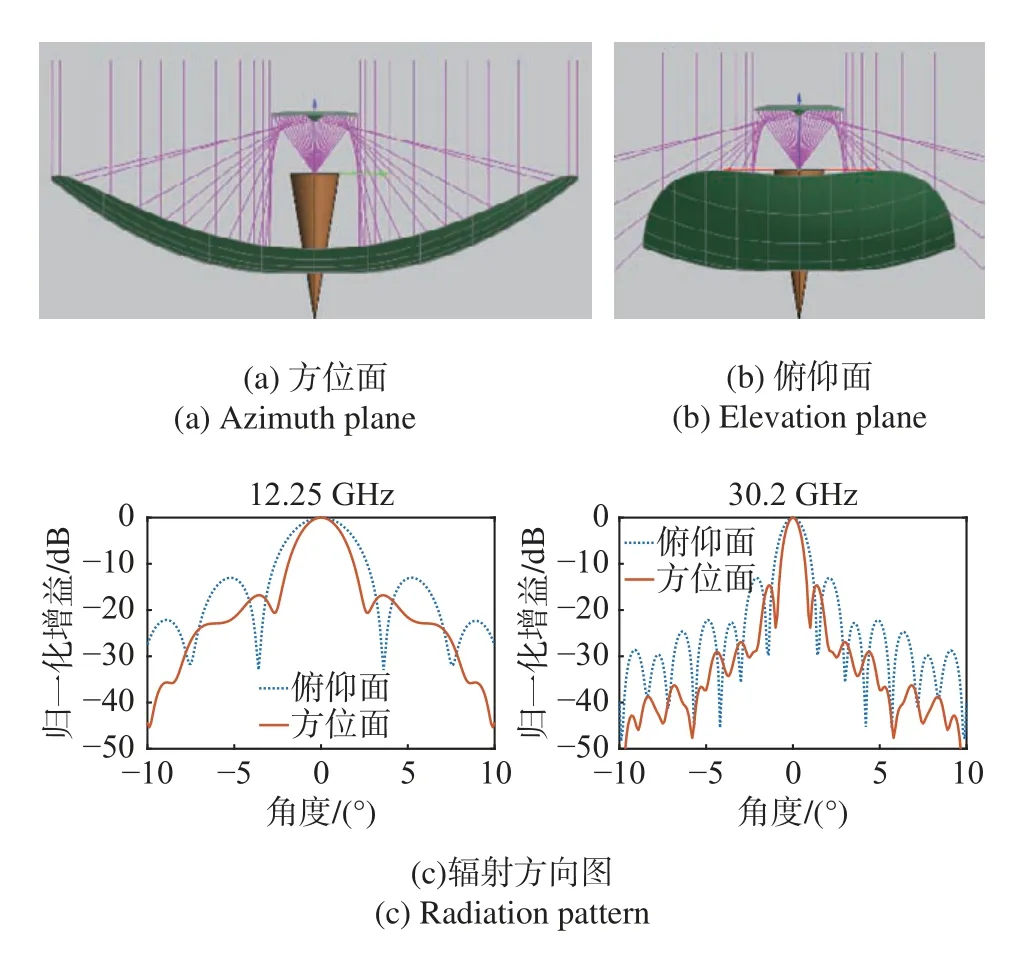
图7 一次优化的天线模型、光路和辐射方向图Fig. 7 The antenna model after the 1st optimization and radiation patterns

将一维口面场优化后的天线主副反射面，分别采用81(n=m=9)个控制点的NURBS 曲面参数化，采用多目标差分进化算法，对天线效率和第一旁瓣进行优化，得到Pareto 最优解集，如图8 所示. 图9 给出了每一代两个目标(天线口面效率和第一旁瓣)最优值的收敛曲线，经过250 次的迭代，两目标均已收敛，天线口面效率收敛在-0.664(66.4%)，第一旁瓣收敛在-18.2 dB.考虑到PO 和PTD 相比于几何光学分析方法有着更高的计算精度，但由于该天线的工作频带宽，馈源和副反射面的间距较近，只有2～4 个波长，馈源和副反射面间的近场耦合较大，需要在设计优化中给第一旁瓣留有较大的设计冗余. 本文的优选解为天线口面效率63.9%，第一旁瓣-17.7 dB，以保证Ku/K/Ka 三频段内的第一旁瓣均低于-14 dB. 建立的天线模型和几何光路如图10 所示，可见副反射面将绝大多数的馈源辐射出的射线截获，并反射在主反射面上，天线在俯仰面的光线明显呈现一定的散焦现象，此现象不同于传统的几何光学设计方法. 图11给出了三种设计方法对应的口面场能量分布，图12中给出了三种设计方法的天线口面效率和第一旁瓣对比曲线，可见，优化一维口面场分布后，天线口面效率提升了5%左右，达到58%～64%，第一旁瓣降低了2 dB 左右，达到-13 dB；综合优化设计方法(即两次优化)提升了天线口面效率3%～10%，达到了59%～67%，并且明显地改善了第一旁瓣5～6 dB，达到了-17 dB. 综合优化设计方法可以有效地减少能量漏失，并优化二维口面场分布，有效地挖掘环焦型椭圆波束天线的性能，实现多频段、高效率、低旁瓣和大轴比的环焦型椭圆波束天线设计. 但综合优化设计方法相对于基于几何光学赋形设计方法的缺点是天线只能工作在所设计的频段之内，设计过程相对复杂，优化设计耗时较长，约十几小时.

图8 Pareto 最优解集和优选解Fig. 8 Pareto optimal solution set and optimal solution

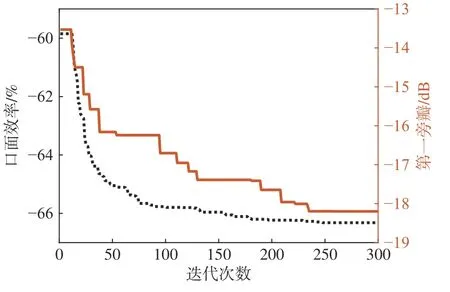
图9 两个目标函数的收敛曲线Fig. 9 Convergence curves of the two objective functions

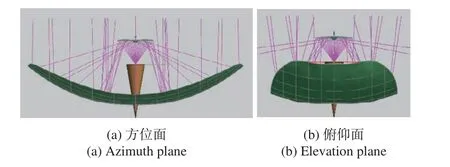
图10 二次优化的天线模型和光路图Fig. 10 The antenna model after the 2nd optimization and optical path diagram

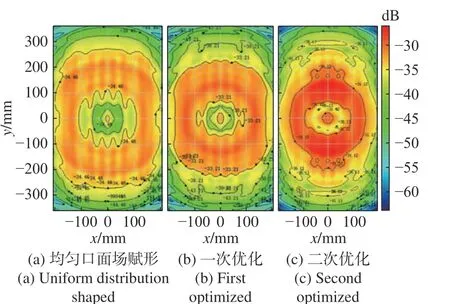
图11 天线二维口面场能量分布Fig. 11 2-D aperture energy distribution of antennas

图12 不同口面场天线效率和第一旁瓣Fig. 12 Efficiency and the first side lobe level of antennas with different aperture distribution

为覆盖Ku/K/Ka 三频段，馈源选用四槽环加载的形式[16]，建立整体天线的全波仿真模型，经全波仿真验证，天线口面效率高于53.5%，旁瓣低于-14.9 dB，驻波比低于1.3∶1. 加工的天线样机照片和仿真模型如图13 所示. 图14 给出测试和计算的天线增益和总效率，其中仿真增益和效率考虑了0.3～0.5 dB 的馈源网络插损. 可见，Ku 和K 两频段内实测总效率均高于49%，Ka 频段总效率高于52%. 在Ku 频段实测和仿真的天线增益和效率基本吻合，在K 和Ka 频段的实测效率比仿真效率低3%左右，其主要原因是高频段对天线主反射面的精度和副面的安装精度更为敏感. 图15 给出了Ku/K/Ka 三个频段测试与计算的天线第一旁瓣，可以看出，测试的俯仰面和方位面的第一旁瓣均低于-14 dB，且计算和测试的第一旁瓣吻合较好，趋势基本相同. 图16 给出了Ku/K/Ka 三个频段5 个频点测试与计算的天线辐射方向图，±5°范围内测试和计算的方向图吻合很好. 此外，测试的VSWR 和计算结果也吻合较好，如图17 所示，且在三频段内测试的VSWR 低于1.44∶1. 上述结果验证了本文设计方法的有效性和正确性.

图13 天线仿真模型和实物照片Fig. 13 Simlulation model and the prototype of antenna

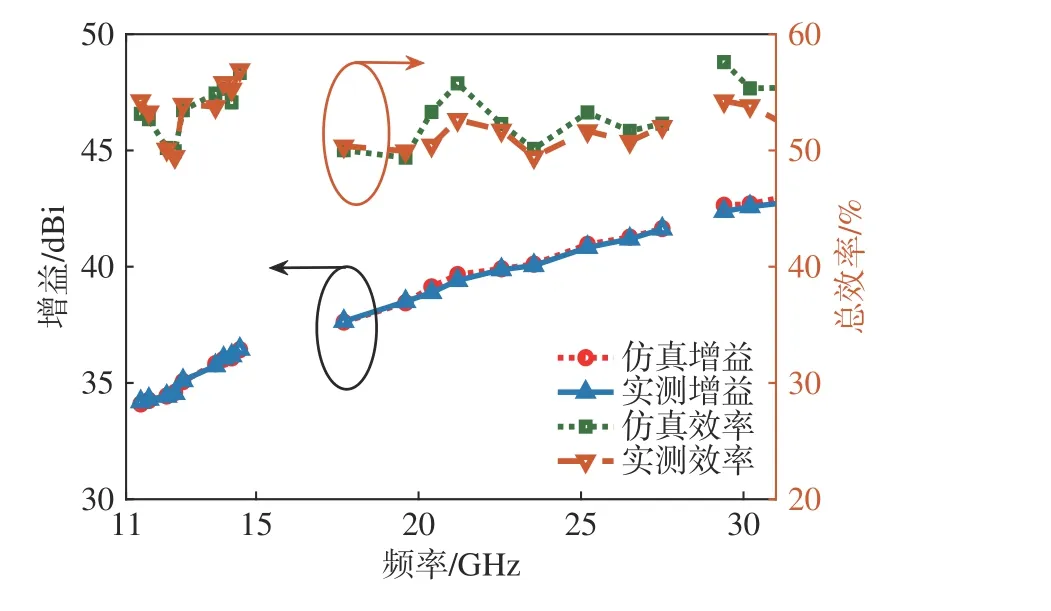
图14 测试和计算的增益和总效率Fig. 14 Measured and calculated gain and total efficiency

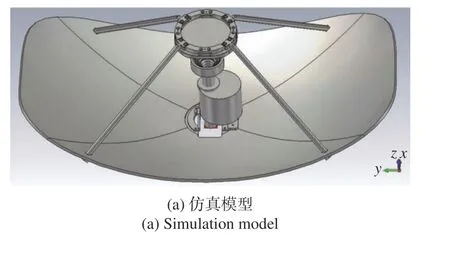
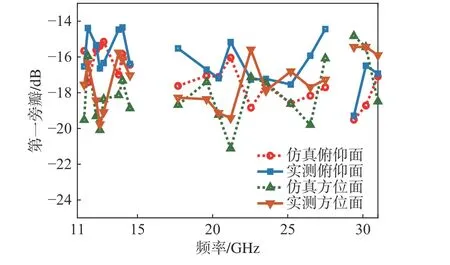
图15 测试和计算的第一旁瓣Fig. 15 Measured and calculated first side lobe level

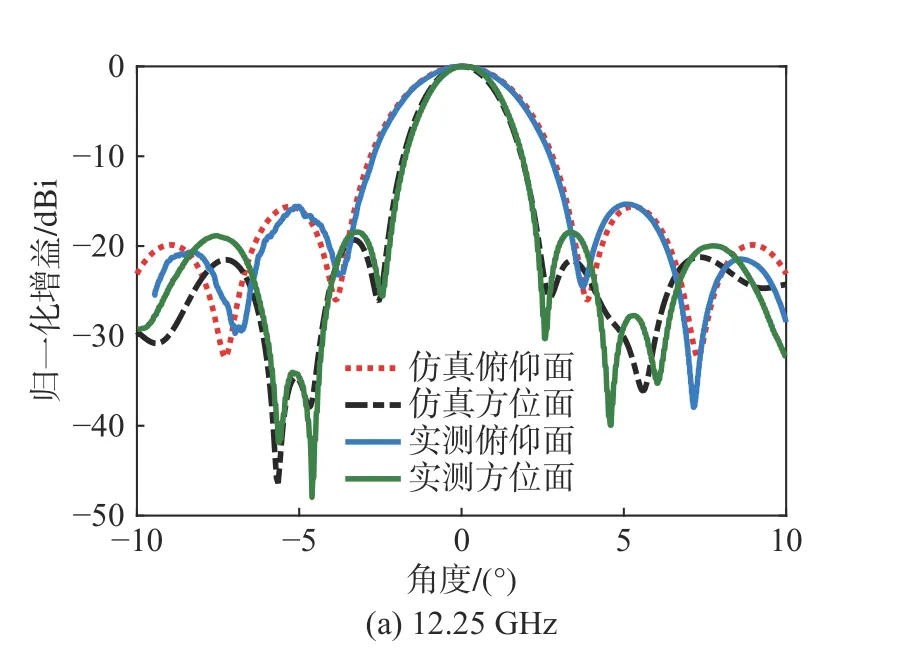
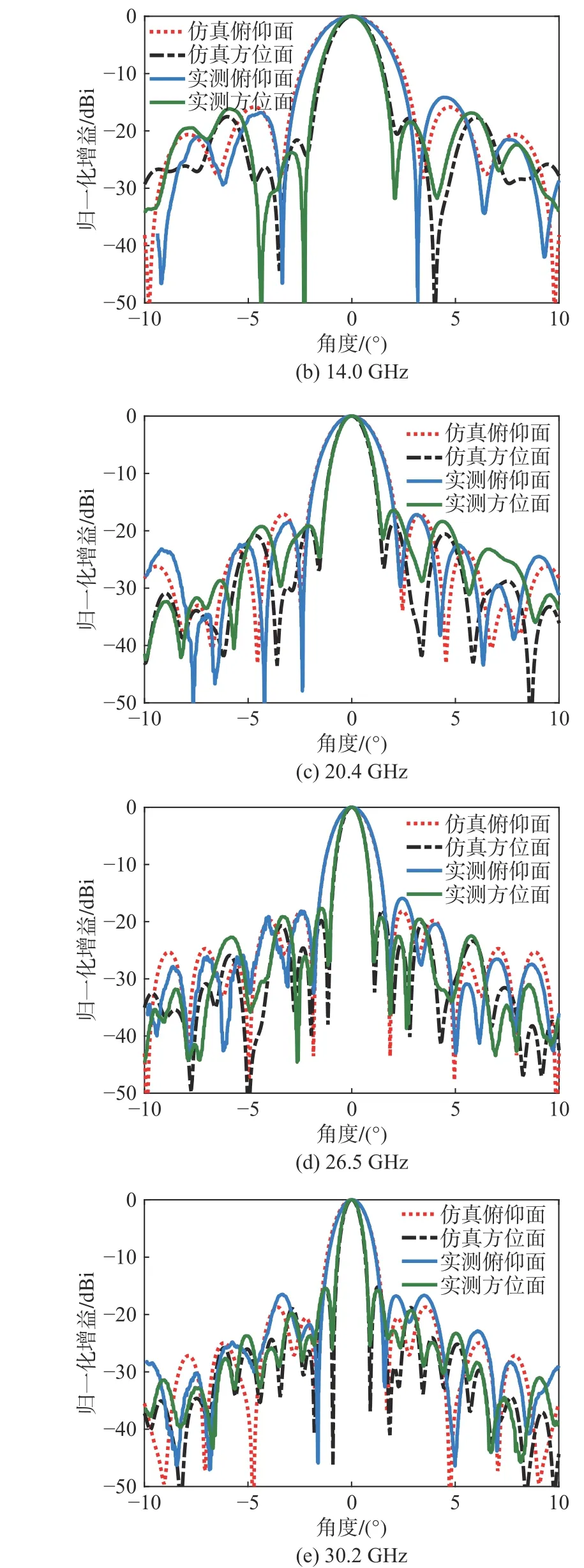
图16 5 个频点测试和计算的天线方向图Fig. 16 Measured and calculated radiation patterns at 5 frequencies

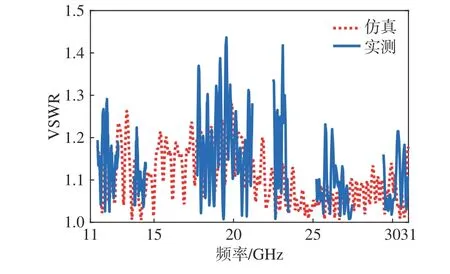
图17 测试和计算的天线VSWRFig. 17 Measured and calculated VSWR of the antenna

4 结 论

本文提出一种基于切割赋形环焦天线和NURBS曲面的环焦型椭圆波束天线的综合优化设计方法，解决了小口径椭圆波束天线馈源网络的遮挡问题，设计的410 mm×720 mm 天线覆盖了Ku/K/Ka 三个频段，实现了低旁瓣、高效率和低剖面的良好性能，验证了设计方法的有效性. 该设计方法还可以用于高性能特殊波束天线的赋形设计.