爆炸成型弹丸贯穿靶板靶后破片空间分布模型
2022-08-06邢柏阳侯云辉张东江杨赵兵徐伟华朱桂利
邢柏阳,郭 锐,侯云辉,骆 强,张东江,杨赵兵,徐伟华,朱桂利,崔 浩
(1. 中国航天科技集团有限公司 第七研究院 第七设计部, 四川 成都 610100;2. 南京理工大学 机械工程学院, 江苏 南京 210094; 3. 西安现代控制技术研究所, 陕西 西安 710065)
深空撞击载荷是一种通过引爆自身携带火药,将爆炸成型弹丸(explosively formed projectile, EFP)以超高速(2 km/s以上)射向被探测小天体表面,制造人造撞击坑,暴露其表面风化层以下物质,为其他探测载荷开展探测或采样提供作业环境的高效式动能探测载荷,对探测小天体内部物质成分和结构特性具有重要意义[1]。但是,在进行深空撞击载荷的地面试验时,只能分析反溅破片云的分布情况,如图1所示[2]。

图1 深空撞击载荷的地面试验[2]Fig.1 Land experiment of deep space impact load[2]
Corvonato等[3]运用Bernoulli双纽线描述了包括反溅破片云在内的完整破片云,发现反溅破片云与靶后破片云的分布存在某种特定的联系。另外,由于钢板的结构较简单,在进行深空撞击载荷相关试验前,有必要先建立EFP贯穿靶板靶后破片空间分布模型。
Piekutowski[4-9]对破片云的结构进行了首次的系统定义,提出了圆柱状弹丸正撞击薄板所产生的破片云的模型,此模型使用圆柱直径、一个径向速度和四个轴向速度表示破片云的运动。Schäfer[10]提出了球形弹丸正撞击薄板产生破片云的模型,并给出了中心破片速度、薄板破片的质心速度、椭球长半轴的速度和椭球短半轴的速度。蒋建伟等[11-13]通过试验和数值仿真建立了工程计算模型,此模型可以很好地预测EFP产生的靶后破片的质量和速度的分布特性。黄炫宁等[14]运用AUTODYN软件中光滑粒子动力学(smoothed particle hydrodynamics, SPH)算法,并结合量纲分析及正交设计理论,建立了EFP正侵彻靶后破片云形状的数学描述模型。在分析靶后破片空间分布时,目前的文献通常是建立靶后破片云的形状方程或分析靶后破片云上个别重要点的速度等,还没有文献分析靶后破片云中所有破片的速度、质量、动能、数量与其空间位置间的关系,更没有文献建立靶后破片来源(靶板和侵彻体)、初始条件(靶板厚度、侵彻体着靶速度)与上述关系间的联系。因此,有必要在考虑EFP变截面特点的基础上,建立EFP贯穿靶板形成的靶后破片的空间分布模型。首先,验证数值仿真方法以及数值仿真结果;然后,分析靶后破片云中所有破片的速度、质量、动能、数量与其空间位置间的关系;最后,用一系列的数值仿真结果验证上述关系。
1 数值仿真模型
1.1 数值仿真方法验证
Dalzell指出,当使用AUTODYN-3D对EFP贯穿钢靶板形成靶后破片进行数值仿真时,SPH方法优于传统的Euler方法和Lagrange方法[15]。因此本文使用AUTODYN-3D中的SPH方法对EFP贯穿靶板形成靶后破片的过程进行数值仿真。本小节将利用文献[11-13]中试验对本文的数值仿真方法进行验证,文献[11-13]中的EFP战斗部均相同,如图2所示。EFP战斗部的装药直径为56 mm,药型罩为壁厚3 mm的球缺形罩,装药为长径比0.86的压装JH-2,壳体厚度为2.52 mm。

(a) 壳体 (b) 主装药(a) Shell (b) Main charge

(c) 药型罩 (d) 压紧环(c) Liner (d) Press-on ring图2 EFP战斗部[11-13]Fig.2 The EFP warhead [11-13]
文献[11-13]中EFP的X光照片如图3(a)下半部分所示,本文所建立的EFP数值仿真模型如图3 (a)上半部分所示。图3 (b)中的红色部分为靶板的固定约束,靶板和EFP的粒子直径均为0.5 mm。

(a) EFP形状 (b) EFP和靶板(a) Shape of EFP (b) EFP and target图3 数值仿真模型Fig.3 Numerical simulation model
文献[11-13]中EFP正侵彻靶板,靶板厚度为20 mm,EFP着靶速度为2 120 m/s,靶板长、宽均为200 mm,本文对此试验进行复现,数值仿真得到的靶后破片云如图4上半部分所示,试验所拍的X光照片如图4下半部分所示。
对比图4(a)和图4(b)的上下部分可以发现,数值仿真复现的结果与试验结果非常吻合,这表明本文的数值仿真方法是具有可靠性的。

(a)80μs时刻的靶后破片云 (b)95μs时刻的靶后破片云(a)Behind-armor debris clouds at 80μs (b)Behind-armor debris clouds at 95μs图4 靶后破片云比较Fig.4 Comparison of behind-armor debris clouds
对比95 μs时刻数值仿真复现的靶后破片云径向膨胀速度与试验结果,如表1所示。

表1 靶后破片云径向和头部膨胀速度Tab.1 Radial and head expansion velocity of the behind-armor debris clouds
由表1可以发现,数值仿真复现的结果与试验结果非常吻合,偏差不超过2%,这表明本文的数值仿真方法是具有可靠性的。
1.2 数值仿真结果验证
为了验证本文数值仿真结果的可信性,针对某典型EFP进行了贯穿靶板的试验。EFP的激光高速摄影如图5上半部分所示,所建立的数值仿真模型如图5下半部分所示。通过幕布墙上已知尺寸的标尺可以换算得到某典型EFP最大长度为98.0 mm,最大半径为28.5 mm。

图5 试验结果和数值仿真模型Fig.5 Experiment result and simulation model
数值仿真模型中靶板的材料为均质装甲钢,状态方程假设为线性;EFP的材料为铜,状态方程假设为Gruneisen,参数取自文献[16-17]。在靶板厚度介于30~70 mm且EFP着靶速度介于1 650~1 860 m/s的条件下,当EFP着靶后经过0.5 ms,侵彻过程已经彻底完成,此时靶后破片的速度、质量、动能、数量以及空间位置已经稳定,不再变化,故取EFP着靶后0.5 ms时刻的数值仿真结果进行统计分析。对比分析SPH粒子尺寸为0.3 mm、0.4 mm以及0.5 mm时的数值仿真结果发现,SPH粒子尺寸为0.5 mm时的结果具备足够的精度并可以节约大量的时间成本。
EFP正侵彻60 mm厚的靶板,测得EFP着靶速度约为1 650 m/s,着靶后0.5 ms时刻的靶后破片云激光高速摄影如图6 (a)所示,对应时刻的数值仿真结果如图6 (b)所示。

(a) 激光高速摄影 (b) 数值仿真(a) Laser high speed photography (b) Numerical simulation图6 EFP贯穿靶板形成的靶后破片云Fig.6 Behind-armor debris cloud formed by the perforation of EFP through the target
由图6可以发现,数值仿真得到的靶后破片云最前端的铜-钢粘结体是由EFP残体和冲塞块顶部共同组成的,这与激光高速摄影得到的图像是相吻合的。另外,二者的靶后破片云轮廓也是接近的。激光高速摄影中靶后破片云的上下不对称,主要是由于EFP的着靶距离很大(100 m),在飞行过程中难免会存在一定的俯仰偏航,使其在着靶时并非严格意义上的正侵彻。尽管EFP在着靶前存在的着靶角很小,但却使得数值仿真的结果与试验所得的激光高速摄影照片有一定差异。但是总体而言,数值仿真中的靶后破片云与试验所得的靶后破片云是基本吻合的,这表明本文的数值仿真结果是具有可信性的。
对比试验中靶后破片云最前端的铜-钢粘结体的轴向速度与数值仿真结果,如表2所示。

表2 铜-钢粘结体的轴向速度Tab.2 Velocity of the steel-copper compound
由表2可以发现,数值仿真所得的靶后破片云最前端的铜-钢粘结体的轴向速度与试验结果相吻合,偏差不超过3 %,这再次表明本文的数值仿真结果是具有可信性的。
将数值仿真得到的钢破片质量与试验结果以及通过文献[18-19]中的理论分析得到的结果作对比,如表3所示。在试验中为了兼顾回收效率以及回收精度,采用了2 mm×2 mm孔径的筛网,可以保障质量不小于0.5 g的靶后破片都能被获取,故仅统计不小于0.5 g的靶后破片。同时,由于试验中铜破片质量为174.90 g,与数值仿真结果765.33 g以及理论分析结果719.80 g差距较大,故不考虑铜破片。

表3 靶板产生的靶后破片质量比较Tab.3 Comparison of mass of behind-armor debris from target
由表3可以发现,数值仿真结果与试验统计结果和理论分析吻合,表明本文的数值仿真结果是具有可信性的。
综上所述,本文的数值仿真结果是具有可信性的,可以利用该数值仿真模型做进一步的分析与研究。
2 靶后破片空间分布模型
后文中的下标t表示靶板产生的靶后破片,下标p表示EFP产生的靶后破片。H0re=H0/D表示相对靶板厚度,H0表示靶板厚度,D=125 mm表示EFP战斗部装药直径。v0re=v0/vint表示相对着靶速度,v0表示EFP着靶速度,vint=1 950 m/s表示EFP成型速度。EFP正侵彻靶板,“不同相对靶板厚度”表示相对着靶速度为0.846 2,相对靶板厚度分别为0.240 0、0.320 0、0.400 0、0.480 0和0.560 0;“不同相对着靶速度”表示相对着靶速度分别为0.846 2、0.861 5、0.892 3、0.923 1和0.953 8,相对靶板厚度为0.320 0。前文验证了数值仿真结果的可信性,为了分析更大的质量范围,故统计质量不小于0.1 g的靶后破片。
2.1 最大相对速度和相对初始条件的关系
vremax=vmax/vint表示靶后破片云中破片的最大相对速度,vmax表示靶后破片云中破片的最大速度。最大相对速度和相对初始条件的关系可以通过一个平面加以表示,如图7所示。图7及后文的图中,Target表示靶板产生的靶后破片,EFP表示EFP产生的靶后破片,后缀Fit表示拟平面。

(a) 靶板产生的靶后破片(a) Behind-armor debris from target

(b) EFP产生的靶后破片(b) Behind-armor debris from EFP图7 最大相对速度和相对初始条件的关系Fig.7 Relationship between the relative maximum velocity and the relative initial condition
图7的拟合平面表达式如式(1)~(2)所示。
vremaxt=-1.233H0re+1.195v0re+0.056 87
(1)
vremaxp=-1.246H0re+1.228v0re+0.043 04
(2)
式(1)~(2)的成立条件均为0.240 0≤H0re≤0.560 0,0.846 2≤v0re≤ 0.953 8,确定系数均为0.98,表明拟合效果良好。由式(1)~(2)可以发现,最大相对速度随相对靶板厚度的减小和相对着靶速度的增加而增加。
(3)
2.2 相对最远空间位置和相对初始条件的关系
xremax=xmax/D表示靶后破片云中破片的相对最远空间位置,xmax表示靶后破片云中破片的最远空间位置,由于本文仅涉及EFP正侵彻靶板,因此该空间位置通常为靶后破片云顶端。相对最远空间位置和相对初始条件的关系可以通过一个平面加以表示,如图8所示。
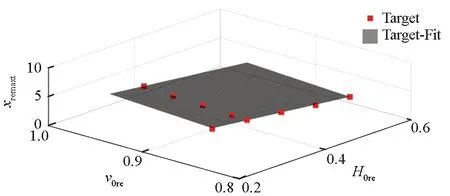
(a) 靶板产生的靶后破片(a) Behind-armor debris from target
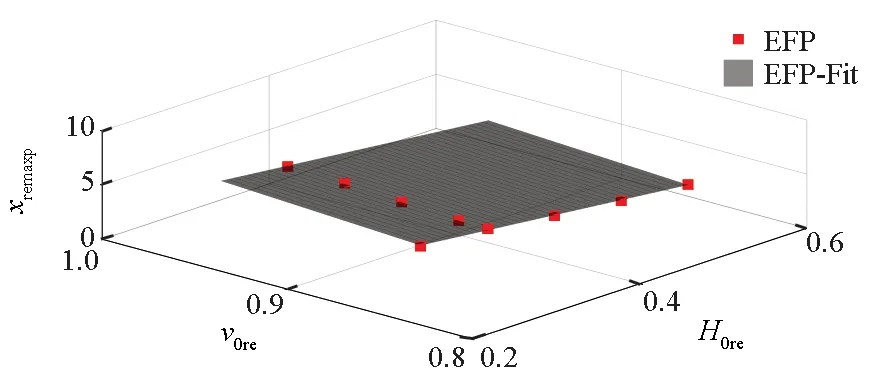
(b) EFP产生的靶后破片(b) Behind-armor debris from EFP图8 相对最远空间位置和相对初始条件的关系Fig.8 Relationships between the relative farthest spatial position and the relative initial condition
图8的拟合平面表达式如式(4)~(5)所示。
xremaxt=-8.592H0re+9.017v0re+0.075 03
(4)
xremaxp=-8.158H0re+9.204v0re-0.324 0
(5)
式(4)~(5)的成立条件为0.240 0≤H0re≤0.560 0,0.846 2≤v0re≤0.953 8,确定系数分别为1.00、0.99。由式(4)~(5)可以发现,相对最远空间位置随相对靶板厚度的减小和相对着靶速度的增加而增加。
2.3 相对速度和相对空间位置的关系
vre=v/vmax表示靶后破片云中破片的相对速度,v表示靶后破片云中破片的速度;xre=x/xmax表示靶后破片云中破片的相对空间位置,x表示靶后破片云中破片的空间位置。相对速度和相对空间位置的关系如图9所示。
从图9(a)~(b)可以发现,vre与xre的关系呈线性,但不同H0re条件下的斜率不同。从图9(c)~(d)可以发现,vre与xre的关系呈线性,不同v0re条件下的斜率无明显差异。另外,可以认为最远空间位置处的靶后破片拥有最大的速度,因此拟合线经过(1,1)点。采用式(6)~(8)对相对速度和相对空间位置的关系进行描述。
vre=λxre+(1-λ)
(6)
(7)
(8)
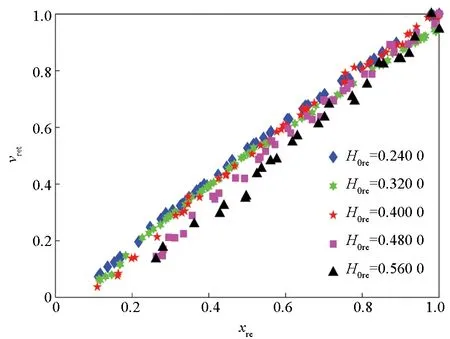
(a) 不同靶板厚度条件下靶板产生的靶后破片(a) Behind-armor debris from target with different target thickness
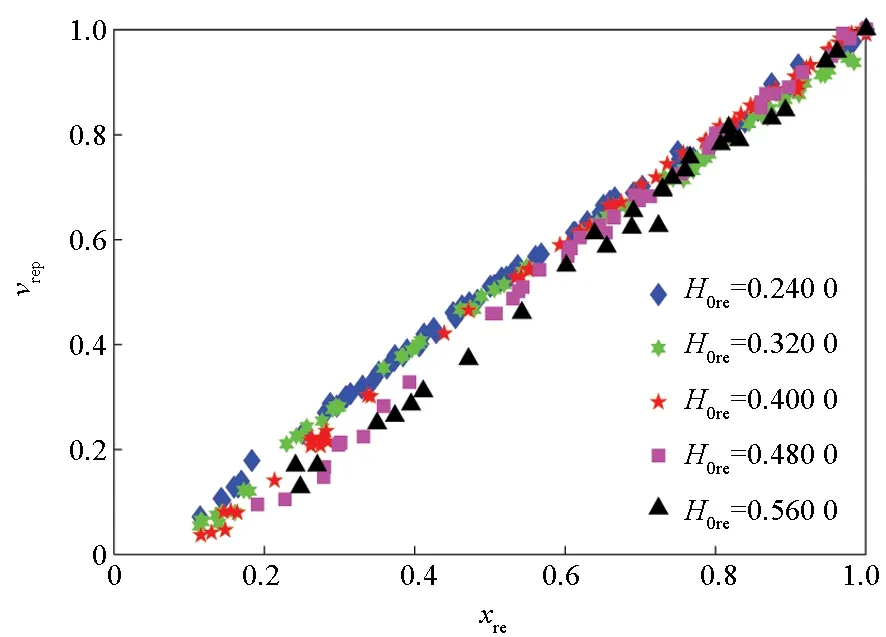
(b) 不同靶板厚度条件下EFP产生的靶后破片(b) Behind-armor debris from EFP with different target thickness

(c) 不同着靶速度条件下靶板产生的靶后破片(c) Behind-armor debris from target with different EFP speed

(d) 不同着靶速度条件下EFP产生的靶后破片(d) Behind-armor debris from EFP with different EFP speed图9 相对速度和相对空间位置的关系Fig.9 Relationships between the relative velocity and the relative spatial position
式(6)~(8)的成立条件为0.240 0≤H0re≤0.560 0,0.846 2≤v0re≤0.953 8。式(7)~(8)确定系数依次为0.98、0.99。从式(7)~(8)可以发现,随着H0re的增加,λt先减小后增加,λp一直增加,并且始终有λt>0、λp>0以及vre始终随着xre的增加而增加。
2.4 相对质量和相对空间位置的关系
mre=m/mto表示靶后破片云中破片的相对质量,m表示靶后破片云中空间位置小于x的破片的质量,mto表示靶后破片云中破片的总质量。相对质量和相对空间位置的关系如图10所示。
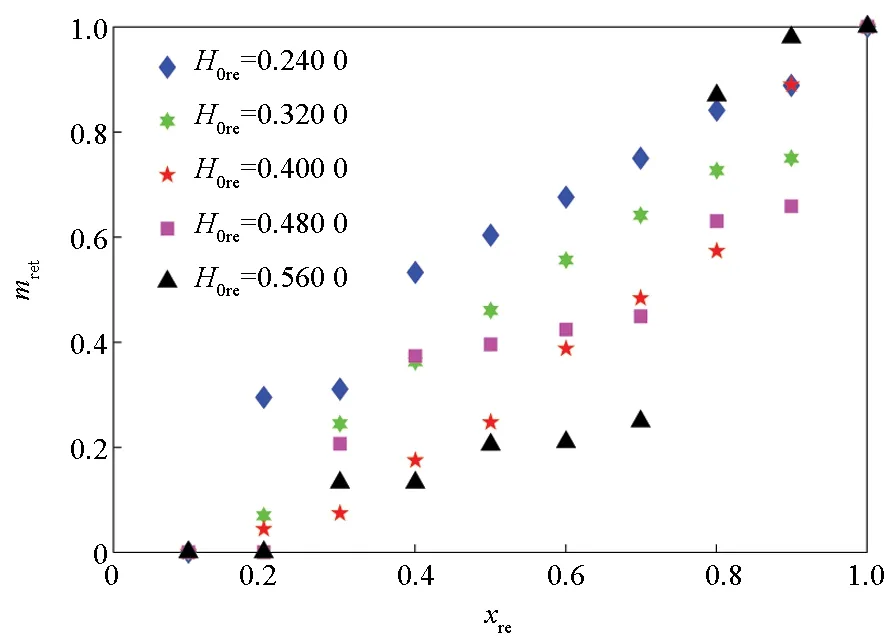
(a) 不同靶板厚度条件下靶板产生的靶后破片(a) Behind-armor debris from target with different target thickness

(b) 不同靶板厚度条件下EFP产生的靶后破片(b) Behind-armor debris from EFP with different target thickness

(c) 不同着靶速度条件下靶板产生的靶后破片(c) Behind-armor debris from target with different EFP speed

(d) 不同着靶速度条件下EFP产生的靶后破片(d) Behind-armor debris from EFP with different EFP speed图10 相对质量和相对空间位置的关系Fig.10 Relationships between the relative mass and the relative spatial position
从图10(a)~(b)可以发现,mre与xre的关系呈幂函数,但不同H0re条件下对应的幂函数关系明显不同。从图10(c)~(d)可以发现,mre与xre的关系呈幂函数,不同v0re条件下对应的幂函数关系无明显差异。另外,由横纵坐标的定义可知,各个工况下的拟合线均经过(1,1)点。采用式(9)~(11)对相对质量和相对空间位置的关系进行描述。
(9)
(10)
(11)
式(9)~(11)的成立条件为0.240 0≤H0re≤0.560 0,0.846 2≤v0re≤0.953 8。式(10)~(11)确定系数分别为0.84、0.99。从式(10)~(11)可以发现,随着H0re的增加,βt一直增加,βp一直减小,并且始终有βt>0,βp>0。
2.5 相对数量和相对空间位置的关系
Nre=N/Nto表示靶后破片云中破片的相对数量,N表示靶后破片云中空间位置小于x的破片的相对数量,Nto表示靶后破片云中破片的总数量。相对数量和相对空间位置的关系如图11所示。

(a) 不同靶板厚度条件下靶板产生的靶后破片(a) Behind-armor debris from target with different target thickness
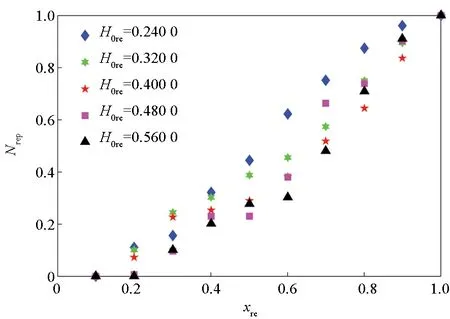
(b) 不同靶板厚度条件下EFP产生的靶后破片(b) Behind-armor debris from EFP with different target thicknes

(c) 不同着靶速度条件下靶板产生的靶后破片(c) Behind-armor debris from target with different EFP speed
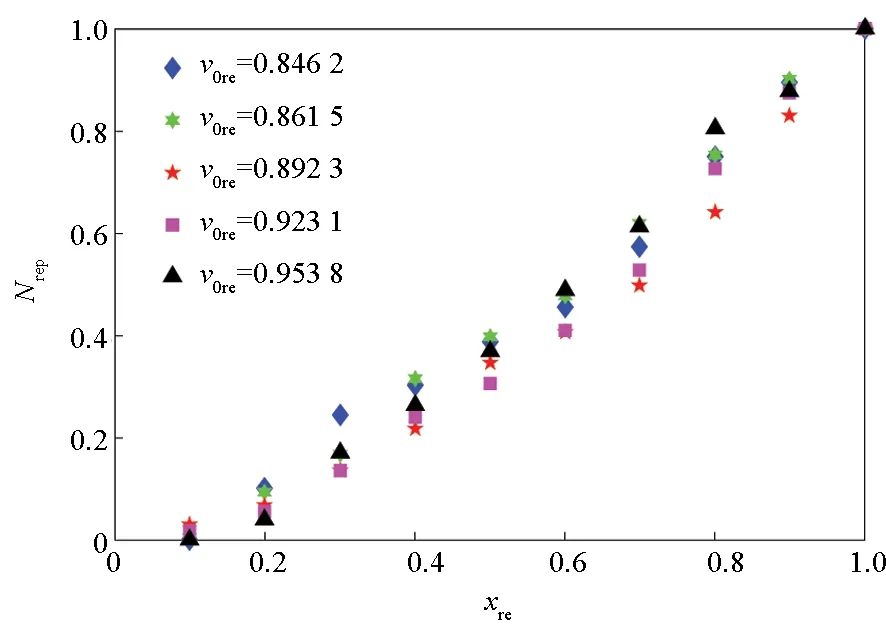
(d) 不同着靶速度条件下EFP产生的靶后破片(d) Behind-armor debris from EFP with different EFP speed图11 相对数量和相对空间位置的关系Fig.11 Relationships between the relative number and the relative spatial position
由图11(a)~(b)可以发现,当v0re一定而H0re变化时,Nre随xre的增加呈幂函数增加。由图11(c)~(d)可以发现,当H0re一定而v0re变化时,Nre随xre的增加呈幂函数增加。另外,由横纵坐标的定义可知,各个工况下的拟合线均经过(1,1)点。采用式(12)对相对数量和相对空间位置的关系进行描述。
(12)
采用式(12)描述各工况时的确定系数如表4所示。从表4可以发现,确定系数均接近于1.00,表明使用式(12)作为上述9种工况下的18组数据的拟合公式是合理的。

表4 各工况下的确定系数Tab.4 Working condition and determination coefficient
3 靶后破片空间分布模型验证
由于在试验中极难准确地测量并统计所有靶后破片的速度(质量、动能、数量)与空间位置的关系、区分靶后破片来源(靶板或EFP),因此进行2组数值仿真,以验证EFP贯穿靶板靶后破片空间分布模型的可靠性。EFP正侵彻靶板,第一组初始条件为H0re=0.480 0、v0re= 0.892 3,第二组初始条件为H0re=0.560 0、v0re=0.861 5。由式(1)~(2)可以得到最大相对速度,由式(4)~(5)可以得到相对最远空间位置,其结果列于表5~6,并与相应的数值仿真结果进行对比。

表5 最大相对速度和相对最远空间位置(第一组)Tab.5 Relative maximum velocity and relative farthest spatial position (the 1st group)
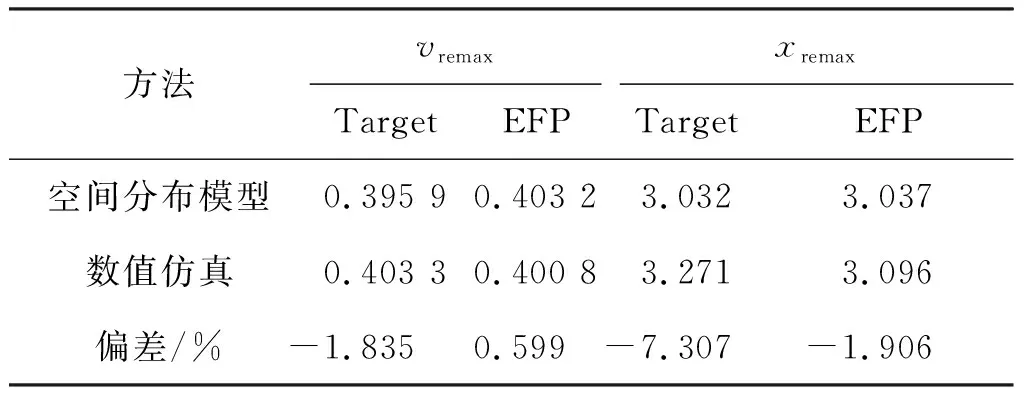
表6 最大相对速度和相对最远空间位置(第二组)Tab.6 Relative maximum velocity and relative farthest spatial position (the 2nd group)
由表5~6可以发现,由空间分布模型得到的最大相对速度和相对最远空间位置与相应的数值仿真的结果均是比较吻合的,表明空间分布模型是可靠的。
设Ekre表示空间位置介于xre1和xre2之间的靶后破片云中破片的相对动能,Ekre=Ek/Eke;Eke表示靶后破片云中破片的最大动能,Eke=0.5·mto·vmax2;Ek表示空间位置介于xre1和xre2之间的靶后破片云中破片的真实动能,Ek=0.5 [(mre1-mre2)mto]·[(vre1+vre2)vmax/2]2;mre1-mre2表示空间位置介于xre1和xre2之间的靶后破片云中破片的相对质量;0.5(vre1+vre2)表示空间位置介于xre1和xre2之间的靶后破片云中破片的平均速度。相对动能与相对空间位置的关系如式(13)。
(13)
第一组的相对动能与相对空间位置的关系如图12所示,曲线由空间分布模型得到,数据点由数值仿真得到,其中,βt=1.951,λt=1.114,βp=4.537,λp=1.108,Δxre=0.1。
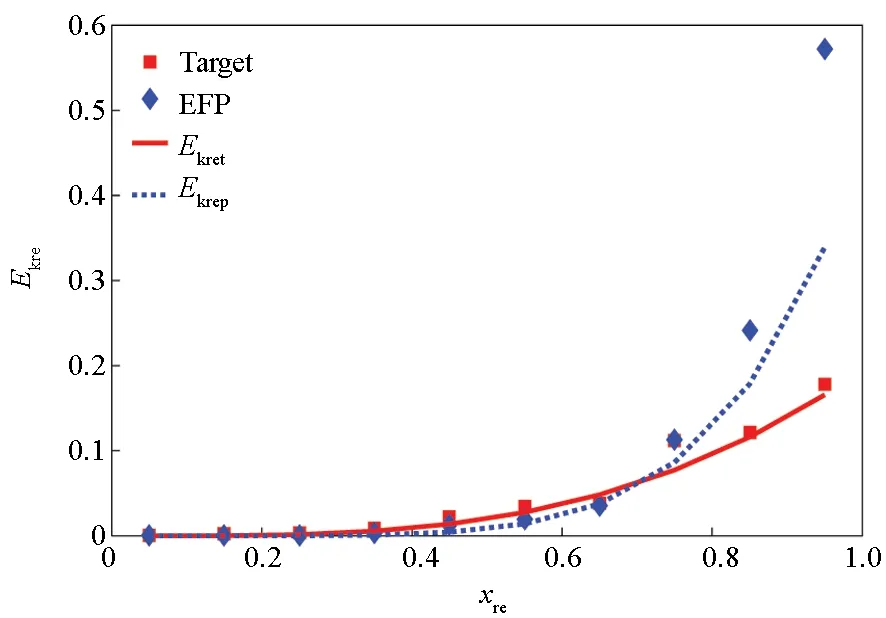
图12 相对动能与相对空间位置的关系(第一组)Fig.12 Relationship between the relative kinetic energy and the relative spatial position (the 1st group)
第二组的相对动能与相对空间位置的关系如图13所示,曲线由空间分布模型得到,数据点由数值仿真得到,其中,βt=2.093,λt=1.208,βp=2.826,λp=1.154,Δxre=0.1。

图13 相对动能与相对空间位置的关系(第二组)Fig.13 Relationship between the relative kinetic energy and the relative spatial position (the 2nd group)
在图12~13中,相对位置介于nΔxre和(n+1)Δxre之间的所有靶后破片的相对动能之和,以横坐标为xre=0.05+nΔxre的点表示,其中n=0,1,2,3,4,5,6,7,8,9。由于此次数据统计中仅收集了10个点,所以曲线不够光滑。从图12~13中可以发现,分布模型均可以有效地预测数据点的变化趋势,以上均表明空间分布模型是可靠的。
第一组的相对数量和相对空间位置的关系如图14所示,曲线由空间分布模型得到,数据点由数值仿真得到。

图14 相对数量和相对空间位置的关系(第一组)Fig.14 Relationship between the relative number and the relative spatial position (the 1st group)
第二组的相对数量和相对空间位置的关系如图15所示,曲线由空间分布模型得到,数据点由数值仿真得到。

图15 相对数量和相对空间位置的关系(第二组)Fig.15 Relationship between the relative number and the relative spatial position (the 2nd group)
图14中靶板和EFP的确定系数分别为0.97和0.98,图15中靶板和EFP的确定系数分别为0.89和0.95,均表明空间分布模型是可靠的。同时,可以发现相对数量随相对空间位置的增加而呈指数增加。
综上所述,空间分布模型是可靠的。
4 结论
本文建立了EFP贯穿靶板靶后破片空间分布模型,考虑了EFP变截面的特点,可以在区分靶后破片来源(来自靶板或EFP)的基础上快速预测靶后破片云中所有破片的速度(质量、动能、数量)与其空间位置的定量关系,可以为建立毁伤评估软件系统奠定基础,为深空撞击载荷相关试验的设计提供一定的指导,并得到以下几点规律。
1)最大相对速度、相对最远空间位置随相对靶板厚度的减小而增加,最大相对速度、相对最远空间位置随EFP相对着靶速度的增加而增加;
2)相对速度总是随相对空间位置的增加而呈线性增加,相对质量、相对数量总是随相对空间位置的增加而呈幂函数增加;
3)通过靶后破片空间分布模型得到的最大相对速度和相对最远空间位置与数值仿真结果偏差的绝对值的均值为4.098%。
4)通过靶后破片空间分布模型得到的相对数量和相对空间位置的关系与数值仿真结果的确定系数的均值为0.95。
致谢
埃因霍温理工大学(Eindhoven University of Technology)的博士生刘磊在论文撰写阶段与作者们进行了富有成果的讨论,谨致谢意!
