东风水电站水轮机效率试验及关系曲线回归分析
2022-08-06许永强
王 磊,许永强
(华电电力科学研究院有限公司,浙江 杭州 310030)
1 问题的提出
为了检测水轮机组的效率及出力特性,使水资源能够得到更加充分的利用,以此来进一步提高发电厂的经济效益,需要对水轮机组进行现场效率试验[1]。通过现场水轮机原型效率试验获取特性曲线,一方面可将其与水轮机厂家提供的特性曲线进行对比,以此作为新机组投运现场验收的一个重要参考[2];另一方面,可以通过该曲线反映出已投运机组的各工况实际运行情况,为水电站乃至电网调度提供支持。
本文拟通过对东风电站1 号机组进行水轮机原型效率试验,获得并整理试验数据,然后对该数据先后进行抛物线及3、4 阶曲线回归分析,对比得到最优拟合关系曲线:水轮机绝对效率拟合曲线及机组耗水率拟合曲线。由拟合曲线可获得该机组动力特性,并以此可为机组、电厂乃至电网优化调度作理论技术支持。
2 机组基本参数
东风水力发电厂位于我国贵州省内,是乌江流域梯级电站中的第二级电站[3]。该电站总装机容量为695 MW(3×190 MW+1×125 MW),4 台机组均为混流式水轮发电机组,其中1~3 号机组单机容量为190 MW,4 号机组单机容量为125 MW。1 号水轮发电机组基本参数见表1。

表1 1 号水轮发电机组主要技术参数表
3 试验参数测量及计算
3.1 流量测量
根据东风发电厂的具体情况,采用电厂机组埋设的超声波流量计测取水轮机流量[4]。
3.2 工作水头计算
工作水头计算公式:

式中:Hn为工作水头(m);Z1为蜗壳进口压力变送器安装高程(m);P1为压力值(kPa);γ为水的容重(kN/m3),在当地试验水温下其值为9.787 kN/m3;V1为蜗壳进口断面平均流速(m/s);g为重力加速度(m/s2),当地值为9.787 m/s2;Z2为尾水水位(m)。
3.3 机组出力计算
机组出力计算公式:
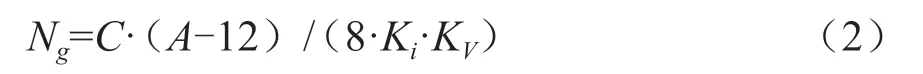
式中:Ng为机组出力(kW);C为功率变送器满量程时的输出功率,其值为0.866 kW;A为功率变送器输出电流(mA);Ki为电流互感器变比系数,本厂取2 400;KV为电压互感器变比系数,本厂取138。
3.4 水轮机效率计算

式中:ηu为机组效率(%);Q为流量(m3/s);Hn为工作水头(m)。

式中:ηt为水轮机效率(%);ηg为发电机效率(%)。
3.5 工作参数换算
进行同一水头效率试验时,按效率不变进行换算:

式中:Q’为换算到平均工作水头下的流量(m3/s);Ng’为换算到平均工作水头下的机组出力(kW);Hnav为平均工作水头(m)。
3.6 机组耗水率计算

式中:q为机组耗水率[m3/(kW·h)]。
4 关系曲线拟合方法
对于水轮机组关系曲线的拟合方法推荐采用最小二乘法[5]。通过该拟合方法可以获得光滑的回归曲线,该曲线能保证各试验工况点与其之间的偏差之和为零,并且使偏差平方和达到最小。
假设水轮机组原型试验一组数据(xi,yi)(i=1,2,…,m),其拟合关系曲线如下:

根据最小二乘法原理使得偏差平方和SSE最小,则可以用数学中求极值的方法,即:。以此求取系数a0,a1,…,an,将此系数代入函数P(x)中即可得出拟合曲线。
相关系数(R2)作为评价回归方程拟合程度优良的重要指标,其计算公式为:
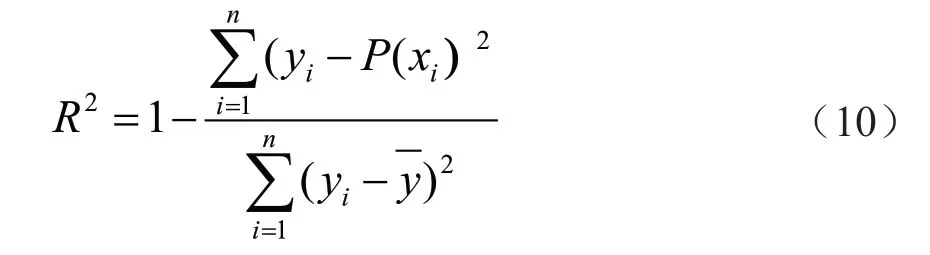
R2值越接近1,则说明拟合效果越好,反之,则说明不存在线性相关关系,曲线拟合效果不佳。除此之外,各系数及回归方程P值、标准误差也常作为评价模型显著性的重要指标[6]。
5 试验结果分析
5.1 试验数据整理
对东风水电站1 号水轮机组进行原型效率试验,稳定上下游水位分别为955.10 m、838.62 m,试验数据见表2。经计算该试验各工况点平均工作水头为114.66 m,并利用公式(5)、(6)将各工况点水轮机的流量和出力换算至平均水头下。

表2 东风发电厂1 号机组实测效率试验数据汇总表
5.2 效率试验不确定度评估
以机组出力168.68 MW 工况点为算例,进行机组效率测试不确定度评估。
(1)电厂采用的超声波流量计的精度为±0.5%,则流量测试系统不确定度为:fSQ=±0.5%
(2)工作水头测试系统不确定度:
选用压力变送器的量程为0~2 MPa,其测量的绝对不确定度:fp=±2 000×0.1%/γ=±0.2 m
压力变送器安装高程测量的绝对不确定度:fs=±0.02 m
下游水位计测下游水位的绝对不确定度:fZ2=±0.02 m
工作水头测试的系统总不确定度:
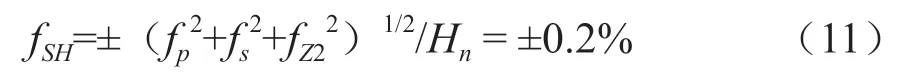
(3)发电机功率测试系统不确定度:
借助互感器测量引起的系统不确定度:

式中:fu为电压互感器变比不确定度,为±0.5%;fi为电流互感器变比不确定度,为±0.5%;δu为电压互感器相角不确定度,为±20′;δi为电流互感器相角不确定度,为±10′;tgφ=0。
得出:ft=±0.5%
发电机功率测量的系统不确定度:
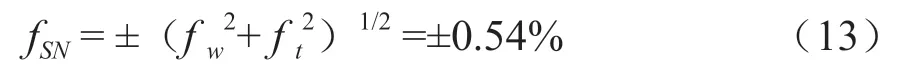
式中:fw功率变送器的系统不确定度,为±0.2%。
(4)效率测试的系统总不确定度:

计算机采集系统的模拟量转换误差以及数据采集的随机误差很小,故在上述精度分析中予以忽略。
5.3 关系曲线回归分析
5.3.1 水轮机效率曲线回归分析
本文采用Rstudio 统计软件对东风水电站1 号水轮机效率试验实测数据分别进行抛物线、3 次多项式、4 次多项式拟合曲线模型回归分析[7],拟合曲线见图1~3。各拟合曲线回归参数见表3~5。

图1 水轮机效率抛物线拟合曲线图

表3 水轮机效率抛物线拟合曲线回归系数表

图2 水轮机效率3 次拟合曲线图
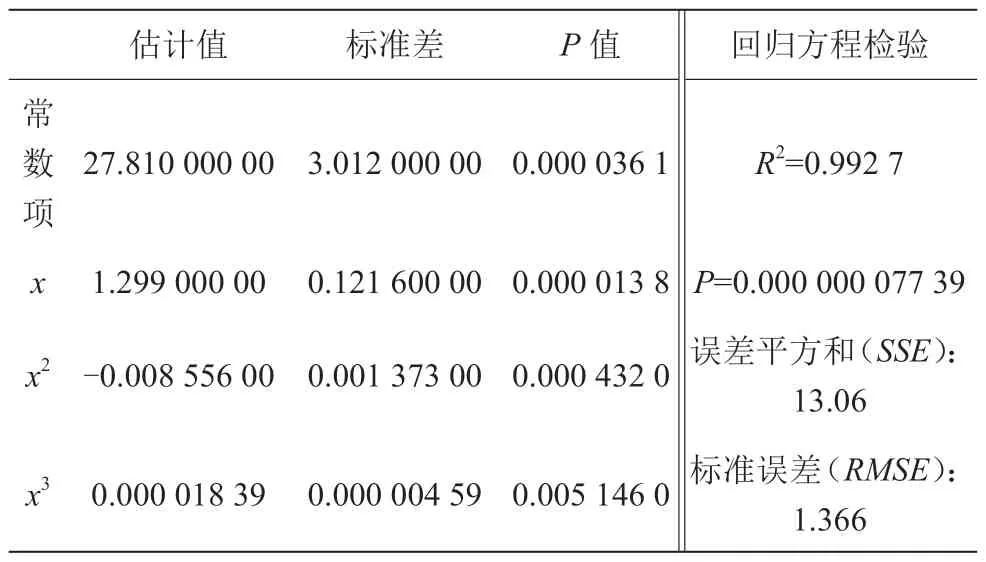
表4 水轮机效率3 次拟合曲线回归系数表
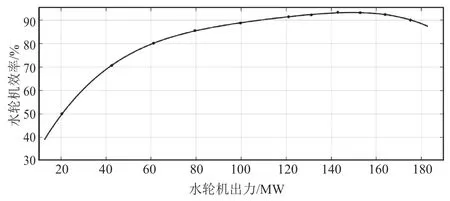
图3 水轮机效率4 次拟合曲线图
由拟合曲线图及回归系数表可以看出,各拟合曲线均比较光滑,拟合优度R2均大于0.9,各模型系数P值均小于0.05,拟合效果良好。通过对比,采用4 次拟合模型,其拟合优度R2、P值、误差平方和及标准误差均优于抛物线及3 次拟合曲线模型。由表5 回归系数表可写出该水轮机效率拟合曲线方程式:


表5 水轮机效率4 次拟合曲线回归系数表
5.3.2 机组耗水率回归分析
机组耗水率曲线采用Rstudio 软件进行拟合,图4 为机组耗水率抛物线拟合曲线图,图5 为机组耗水率4 次拟合曲线图,拟合曲线回归系数结果见表6~7。
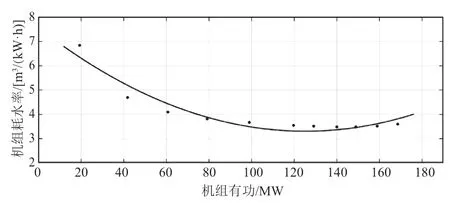
图4 机组耗水率抛物线拟合曲线图
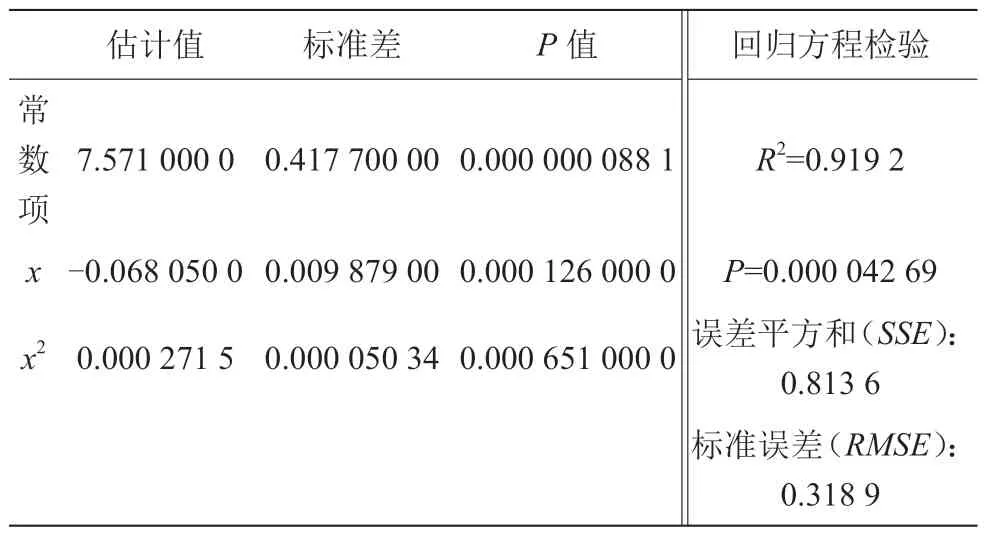
表6 机组耗水率抛物线拟合曲线回归系数表
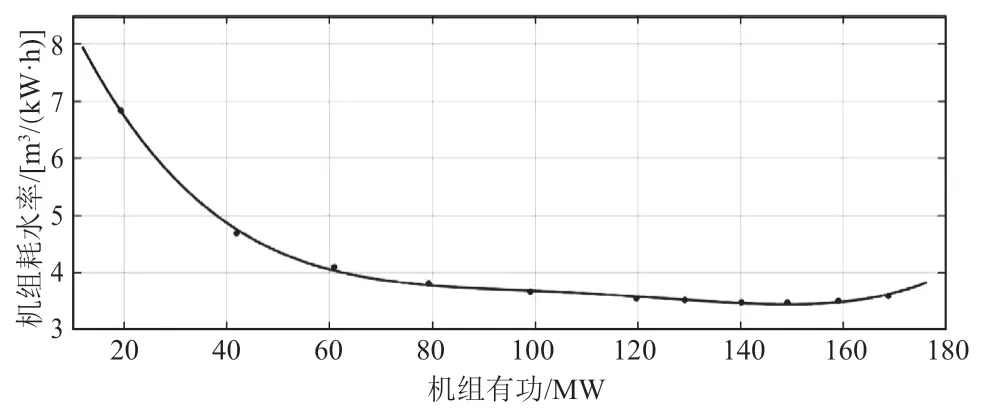
图5 机组耗水率4 次拟合曲线图
对比机组耗水率各拟合模型,采用4 次拟合模型,其拟合优度R2、P值、误差平方和及标准误差同样优于抛物线拟合模型。由表7 可得出该机组耗水率拟合曲线方程式:

表7 机组耗水率4 次拟合曲线回归系数表
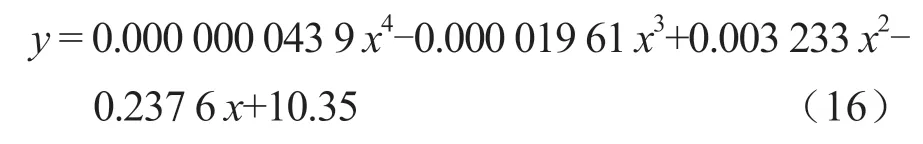
6 结论
由试验及回归分析结果可知,根据水轮机组原型效率试验数据选择合适的回归模型非常重要,同时也要保证测量数据的准确性、可靠性,因为拟合曲线精度的优良取决于单个测点测量误差及试验工况点数。只有回归曲线的拟合精度提高才能够准确反映出水轮机组的实际情况,才能对机组运行、调度乃至未来特性预测作技术支持。
