基于VMD能量熵的混合双端直流输电线路纵联保护方案

高淑萍，宋晓辰，宋国兵

基于VMD能量熵的混合双端直流输电线路纵联保护方案

高淑萍1，宋晓辰1，宋国兵2

(1.西安科技大学电气与控制工程学院，陕西 西安 710054；2.西安交通大学电气工程学院，陕西 西安 710049)

为提高混合双端高压直流输电线路故障快速清除能力，确保输电系统安全运行，提出了一种基于变分模态分解(Variational Mode Decomposition, VMD)能量熵的混合双端直流输电线路纵联保护方法。根据高压直流输电线路边界元件两侧的电压能量不同，同时考虑故障类型以及过渡电阻的影响，构造了电压故障分量的能量熵保护方案。将故障时测量点采集的电压故障分量进行VMD分解，得到若干固有模态分量并计算能量熵。根据区内外故障时电压故障分量的能量熵大小不同构造区内外故障判据，由正负极电压故障分量的能量熵之比构造故障极判据。通过PSCAD/EMTDC建模仿真，并利用Matlab结合保护判据对该方法进行验证。结果表明，该保护方法快速性好、可靠性高、耐过渡电阻能力强。

混合双端直流输电系统；继电保护；故障；变分模态分解；能量熵

0 引言

高压直流输电系统由于其传输容量大且损耗小的优点，广泛应用于远距离、大容量输电[1-3]。电网换相型换流器高压直流输电系统(Line Commutated Converter based High Voltage Direct Current, LCC HVDC)存在逆变站易发生换相失败、无功功率消耗大等缺点。模块化多电平换流器高压直流输电系统(Modular Multilevel Converter based High Voltage Direct Current, MMC HVDC)不存在换相失败问题，且有功功率和无功功率能独立控制。结合LCC和MMC两者优点，整流站采用LCC、逆变站采用MMC的混合型高压直流输电成为当前研究热点[4]。然而基于半桥子模块(Half Bridge Sub-module, HBSM)的MMC无法像LCC那样单纯依靠换流器控制策略来完成直流侧故障穿越。基于全桥子模块(Full Bridge Sub-module, FBSM)的MMC虽可以通过调制运行实现直流故障穿越，提高直流电压利用率，但与同容量和同电压等级的半桥MMC相比，全桥MMC使用的电力电子器件较多，不仅增加了投资的成本，而且引入更多的运行损耗。因此，将两种子模块混合使用，形成混合MMC，可以充分发挥各自优势，具有良好的经济性和故障穿越能力，使LCC-MMC混合高压直流输电结构在远距离输电场合有更好的工程应用前景[5-7]。

由于直流输电系统输电线路较长，发生故障的几率较高。故障发生后，如何快速稳定可靠地识别故障并使继电保护装置动作，成为直流输电亟待解决的问题。近些年来，针对高压直流输电线路保护，国内外学者做了大量的研究：文献[8]提出了一种采用补偿电流的高压直流输电线路保护方法，通过基于分布参数模型的HVDC输电线路区内外故障时不平衡电流不同，确定保护整定判据。文献[9-10]利用边界元件对高频信号的阻滞性，分析单端暂态电气量信号，通过边界元件阻抗幅频特性，构建区内外故障识别判据。文献[11]提出一种基于小波多频带能量的HVDC线路单端暂态电流保护方案。利用低频带能量、高频带和低频带能量比来区分区内外故障、故障性雷击和非故障性雷击，利用正极和负极的能量比确定故障极。文献[12]根据平波电抗器两侧有功功率故障分量暂态能量的不同，利用小波包对有功功率故障分量分解，整定保护判据，即可区分区内外故障和故障极。文献[13]提出了一种基于经验模态分解与斯皮尔曼相关系数的混合直流线路纵联保护方法，通过EMD提取故障信号残余函数，计算残余函数的Spearman相关系数，识别区内外故障。文献[14]利用改进局部均值分解方法提取故障分量，根据线路区内外故障时故障电压分量瞬时能量差值的不同特征，提出一种基于改进LMD分解的直流线路暂态保护方法。

VMD算法是2014年Dragomiretskiy等人提出的一种新型信号分解方法，早期VMD算法用于机械故障诊断[15-16]，近年来在电力系统中，该分解方法已在变压器故障诊断[17-18]和高压直流输电线路故障测距[19-21]中应用，但在高压直流输电线路保护中应用较少。文献[22]利用VMD良好频带划分能力，将信号划分为不同频率的模态分量，可以将其应用到谐波信号的检测当中。该算法具有良好的噪声鲁棒性和较高的检测精度，可同时适用于稳态谐波与暂态谐波的检测。

本文提出一种基于VMD能量熵的纵联保护方法，利用VMD分解故障电压信号，根据直流线路区内外故障时电压故障分量的VMD能量熵不同，区分区内外故障，根据直流线路区内故障时正负极电压故障分量的能量熵之比不同区分故障极。本文搭建±500 kV混合双端直流输电系统的模型，通过大量仿真试验验证本保护方法的正确性。

1 混合双端直流输电系统拓扑结构

本文搭建了直流电压等级为±500 kV混合双端直流输电系统模型，整流侧采用LCC型换流器，逆变侧采用MMC型换流器，每个换流器由50%全桥子模块和50%半桥子模块混合级联而成，如图1(b)所示。其中整流侧的换流器采用定直流电流控制，逆变侧的换流器采用定直流电压和定无功功率控制。

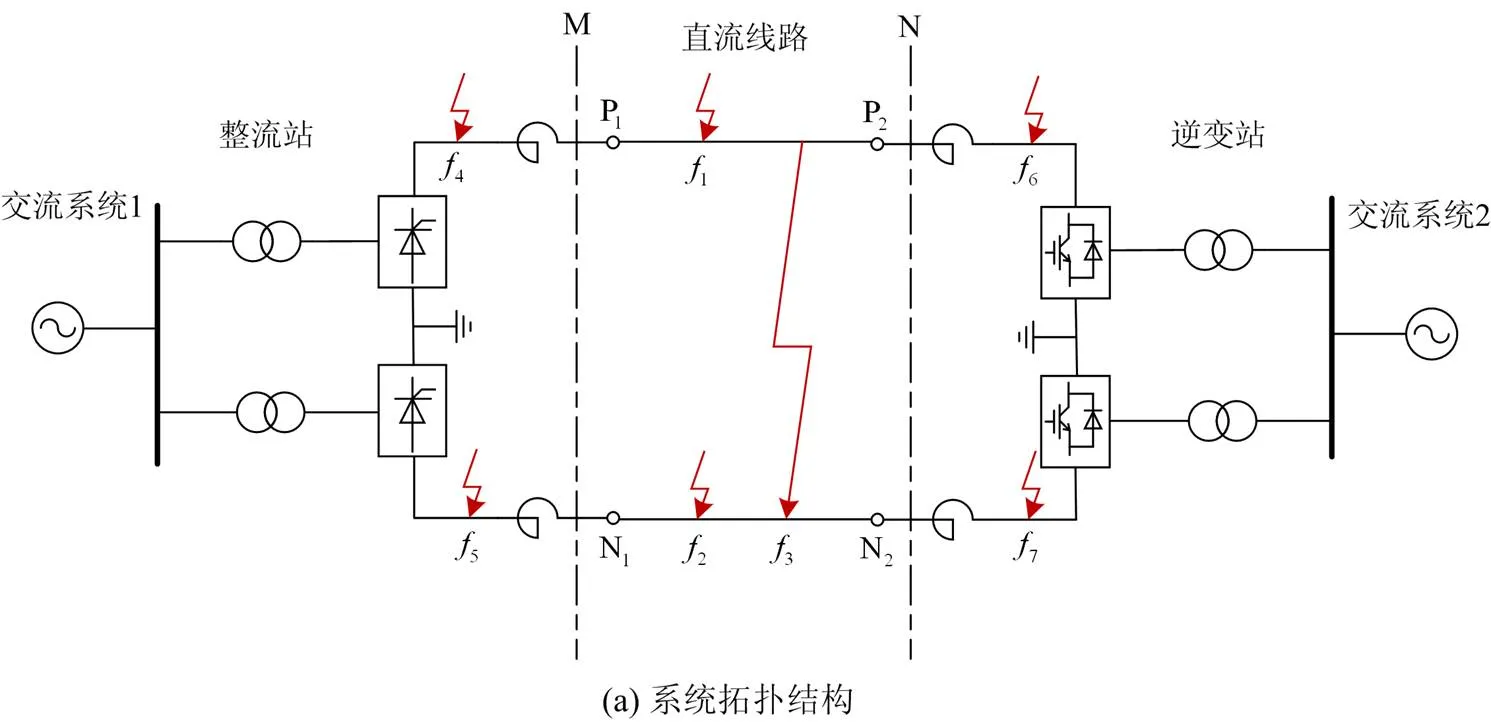
2 直流输电线路故障特性分析

2.1 边界保护

在本次搭建的直流线路中，平波电抗器可以作为天然物理边界，将混合双端线路保护分成区内和区外两个部分，边界元件对暂态电压信号的变化有衰减作用。平波电抗器主要参数为电感值，电感值取值越大，对高频分量抑制效果越好，但太大会引起过电压，系统自动调节性能也将变差[23]。在本文采用的模型中，经大量仿真实验，电感值最小取值为100 mH，当电感值小于100 mH时，虽然边界可以区分，但直流电流纹波难以抑制。本文中电感值取300 mH。当平波电抗器取300 mH时，可抑制直流纹波，且边界效应明显。

2.2 区内故障特性分析

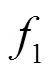
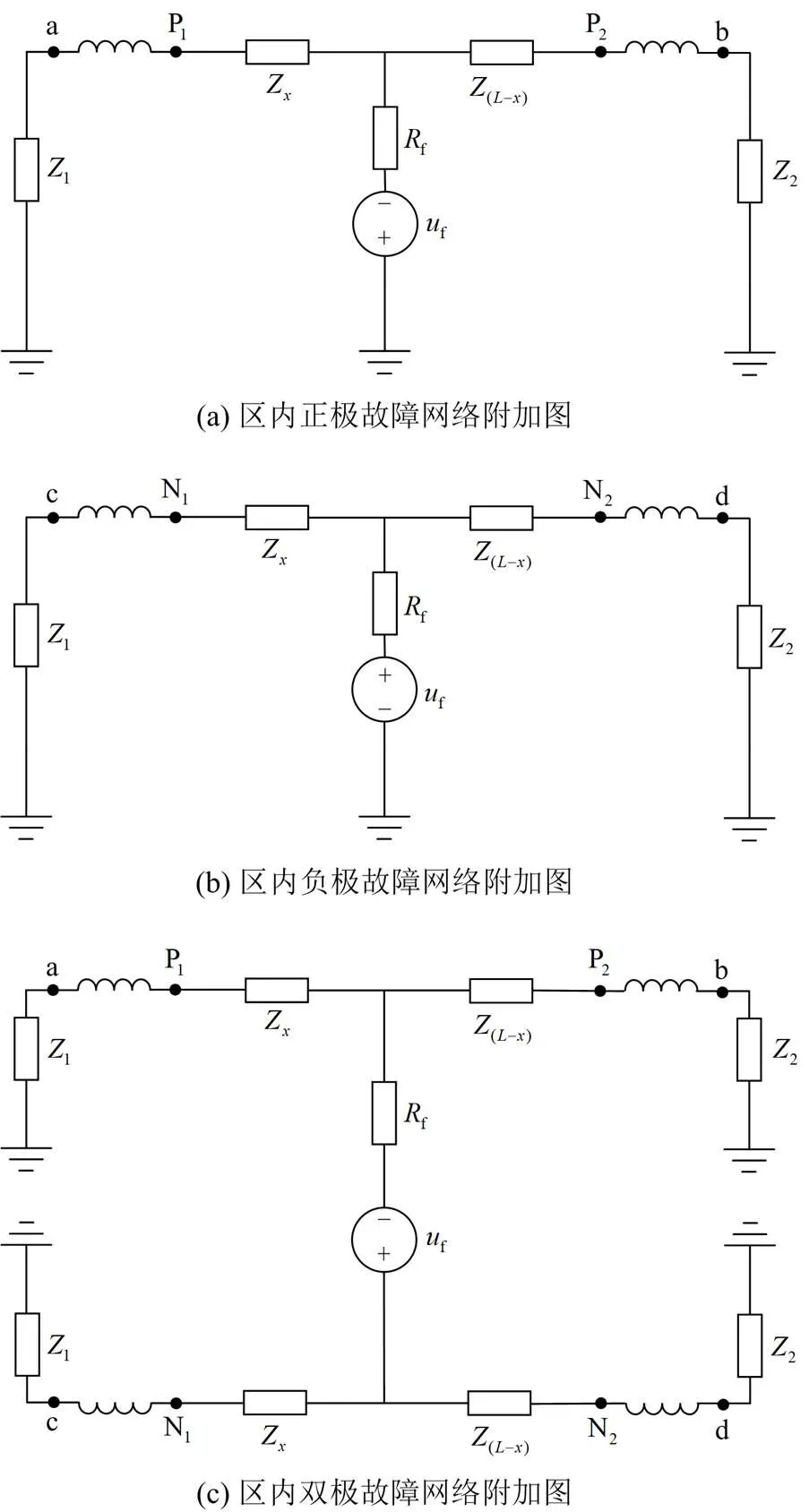
图2 区内故障网络附加图

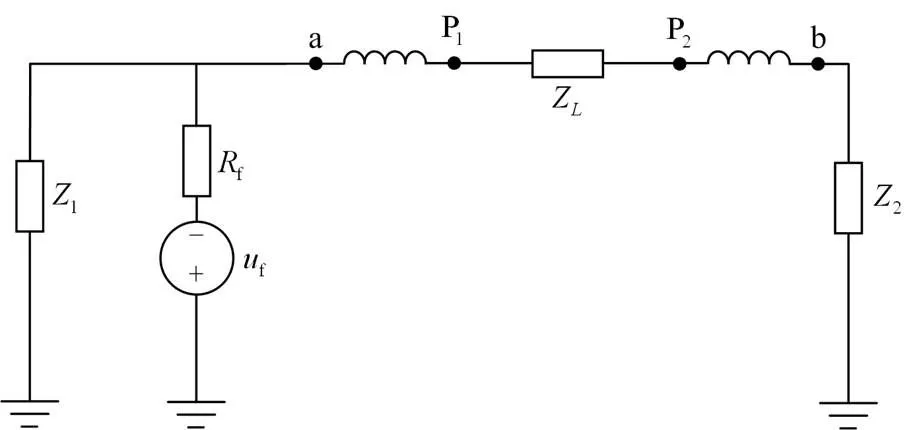
图3 区外故障网络附加图

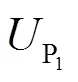
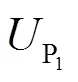
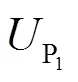
2.3 区外故障特性分析

由此可知，当发生区外故障时，由于有边界元件的存在，保护测量安装处得到的电压故障分量变化较小，电压故障分量的暂态能量较小。

3 相关理论和算法

3.1 变分模态分解

变分模态分解(VMD)是一种自适应、完全非递归的模态变分和信号处理的方法[24]，其利用循环迭代求取约束变分问题的最优解，根据实际情况确定模态分解个数。随后在搜索和求解过程中自适应匹配每种模态的最佳中心频率和有限带宽，进而把原始信号分解为一系列不同频率的固有模态分量，实现固有模态分量的有效分离、信号的频域划分，进而得到给定信号的有效分解成分，最终获得变分问题的最优解。

该算法利用维纳滤波构造了原始信号()的变分问题，将原始信号分解成个本征模态IMF分量，保证分解序列为具有中心频率和有限带宽的IMF分量。构造的约束性变分表达式为

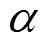
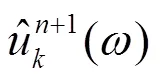
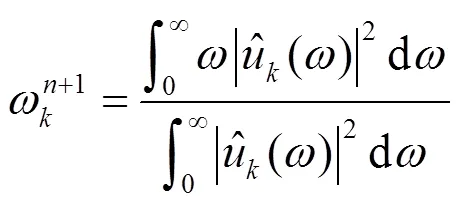
式中，为噪声容限参数。

变分模态分解具体实现过程如下：

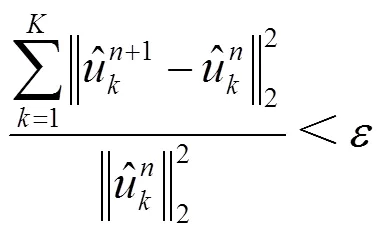
3.2 算法参数设置

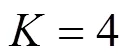
3.3 VMD能量熵

信息熵是对系统不确定性的度量化，即信号输出的信息越多，则不确定性越大，得到的熵值越大。反之，信号输出的信息越少，则不确定性越小，得到的熵值越小。将信息熵运用在直流输电系统中，当故障电压分量变化越大时，得到的暂态能量越多，其能量熵值越大，当故障电压分量变化越小时，得到的暂态能量越少，其能量熵值越小。

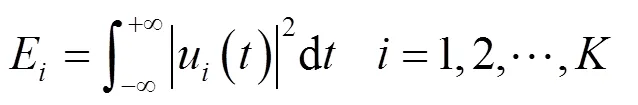
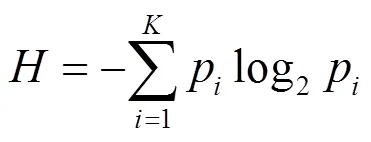
由于边界元件的抑制作用，当直流线路发生区内故障时，保护测量安装处电压故障分量的暂态能量较大，当直流线路发生区外故障时，保护测量安装处电压故障分量的暂态能量较小，其VMD能量熵值不同，所以可利用计算VMD能量熵的办法来识别区内外故障状态。

4 基于VMD能量熵的保护方法

4.1 保护启动

直流线路故障时，提取保护安装处的电压故障分量幅值，构造出保护启动判据。

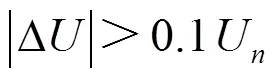
4.2 保护判据

4.2.1区内外故障识别判据

当直流输电线路确定发生故障时，应首先判断故障发生在区内还是区外。通过2.3节分析可知，直流线路发生区内故障时，保护测量点得到的电压故障分量的暂态能量较大，VMD能量熵值较大，当发生区外故障时，保护测量点得到的电压故障分量的暂态能量较小，VMD能量熵值较小。由此，构造区内外故障识别判据。

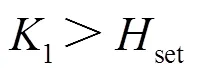
4.2.2故障极识别判据

当直流线路发生区内故障时，需进一步识别故障是发生在正极、负极或者双极线路，即需要判别故障极。当直流线路发生区内正极故障时，正极保护测量安装处的电压故障分量的能量熵远大于负极保护测量安装处，当直流线路发生区内负极故障时，负极保护测量安装处的电压故障分量的能量熵远大于正极保护测量安装处，当直流线路发生区内双极故障时，正极保护测量安装处的电压故障分量的能量熵与负极保护测量安装处的大小相近。

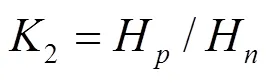
最终，构造的保护判据如下。

4.3 保护流程

图4为保护方法流程图，先判断是否发生故障，当保护启动时，对测量得到的数据进行VMD分解，求取能量熵，对比正负极能量熵大小，从而判别区内外故障，以及故障选极。

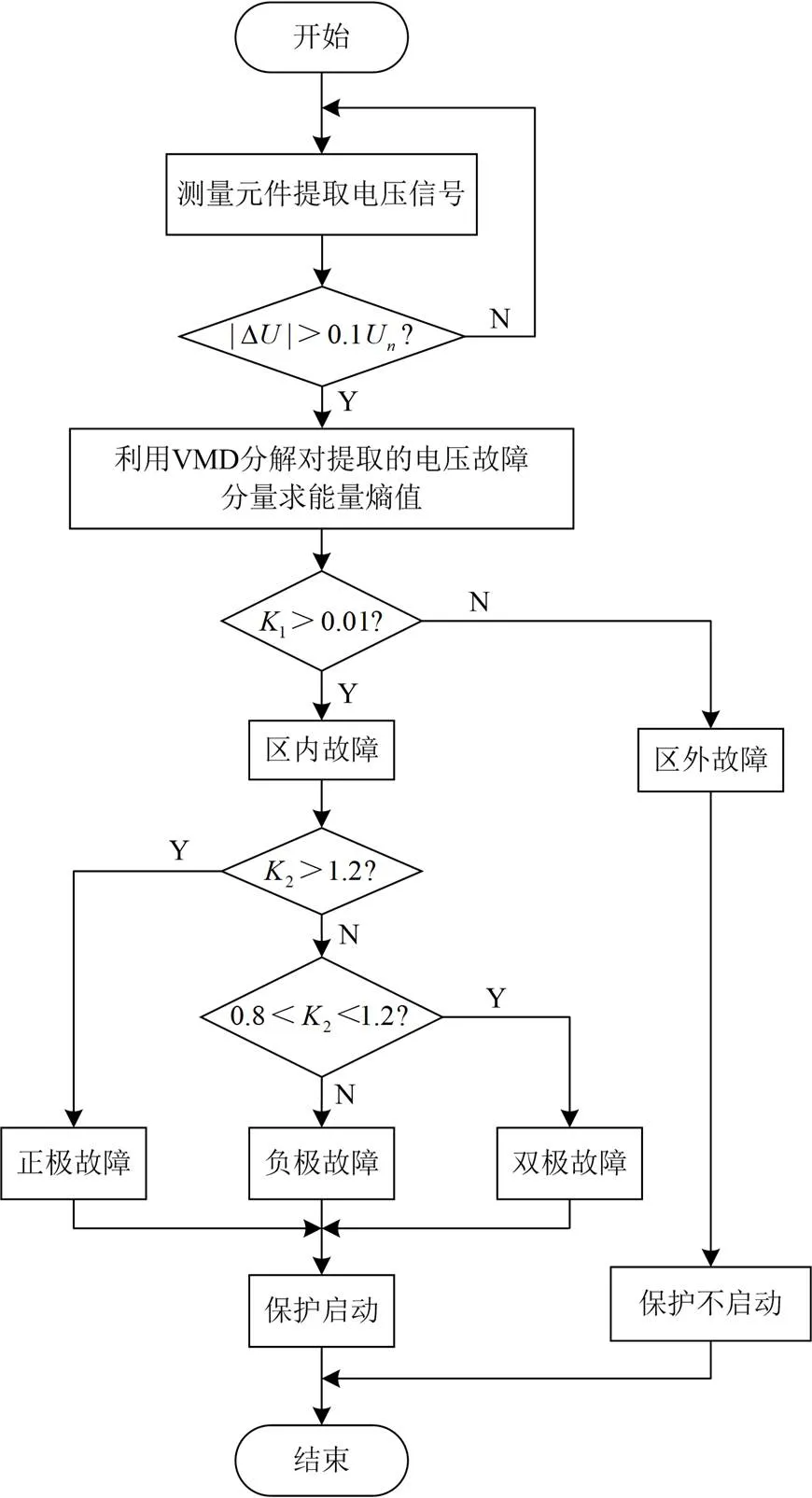
图4 保护方法流程图

5 仿真验证与分析

本文搭建的混合双端直流模型输电线路长度为800 km，仿真时长2 s，在1 s时设置故障，故障持续时间为0.1 s，故障采样窗口设为3 ms，采样频率设为10 kHz。

5.1 区内外故障仿真

5.1.1金属性接地故障

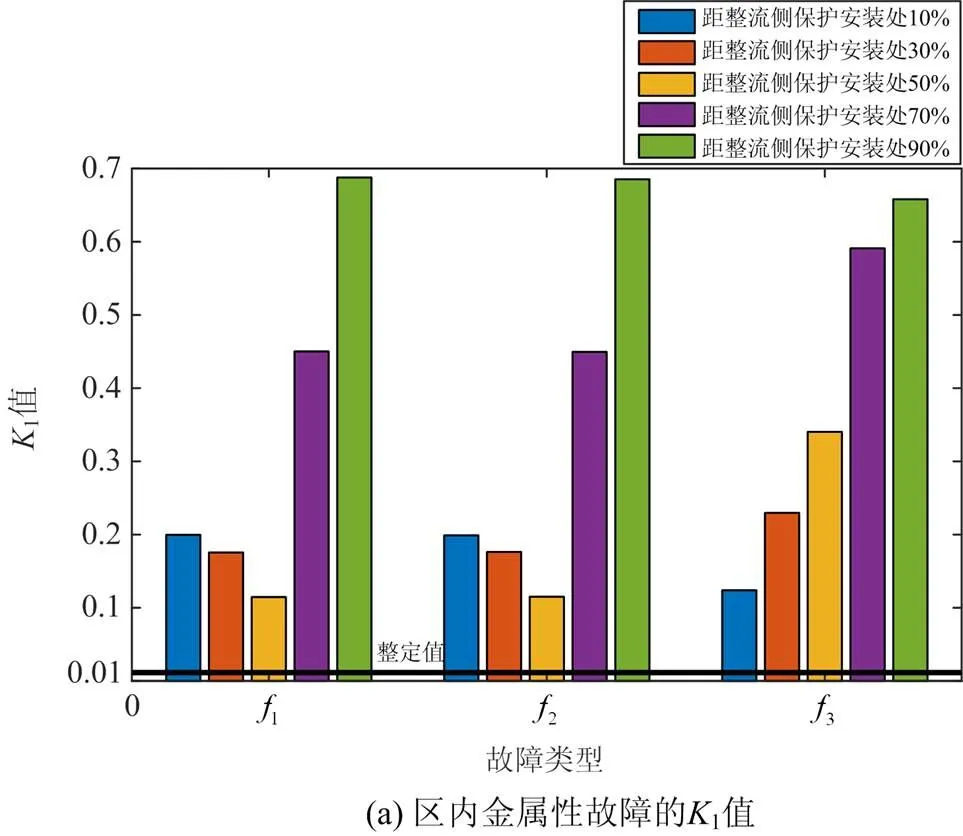
当过渡电阻为0.01 Ω时，在不同故障类型和不同故障位置下，测量点得到的能量熵值如表1所示。

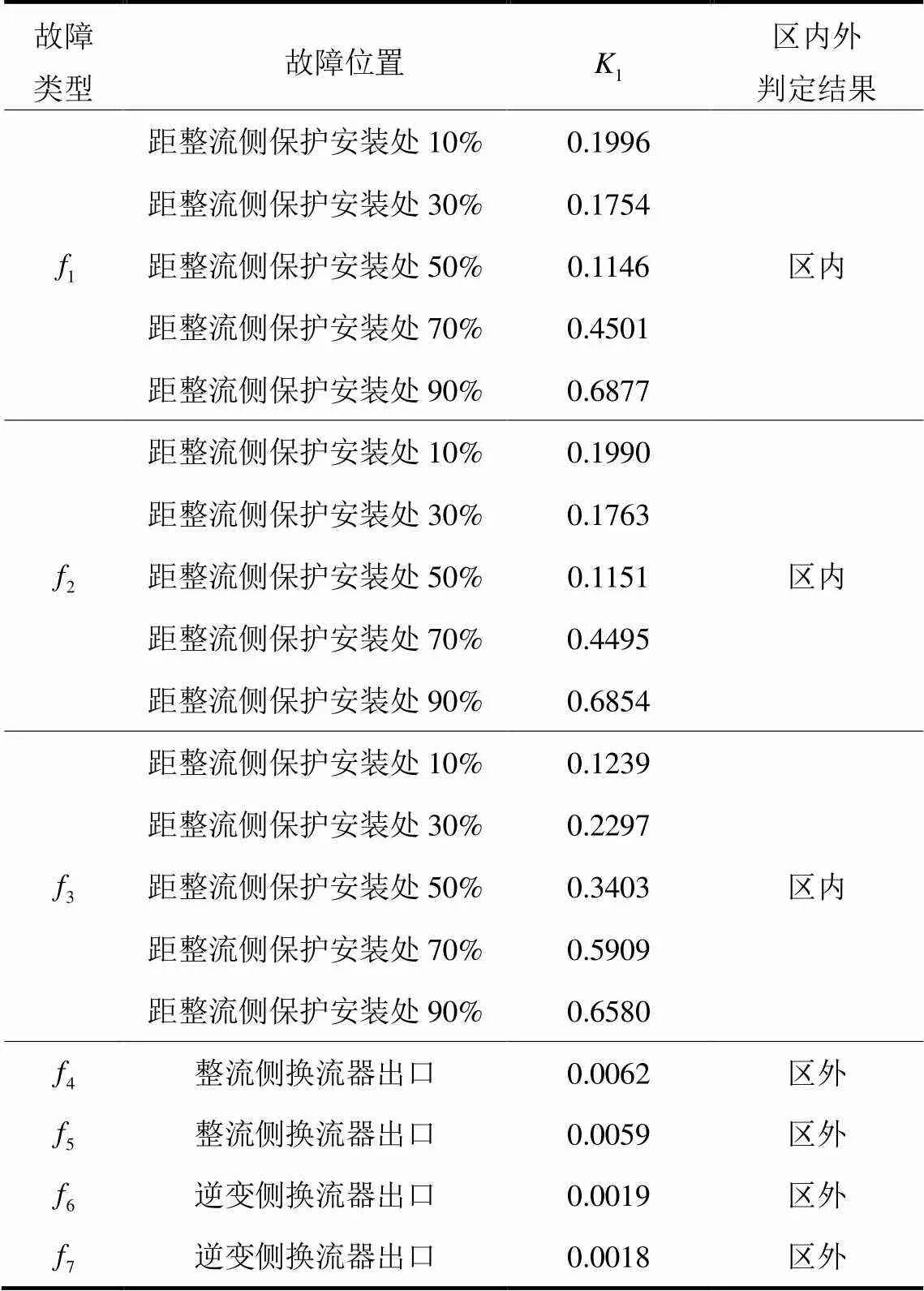
表1 区内外金属性短路故障识别结果

5.1.2高阻接地故障

过渡电阻为100 Ω、300 Ω、500 Ω时，在不同故障类型和不同故障位置下，测量点得到的能量熵值如表2所示。

5.2 故障选极

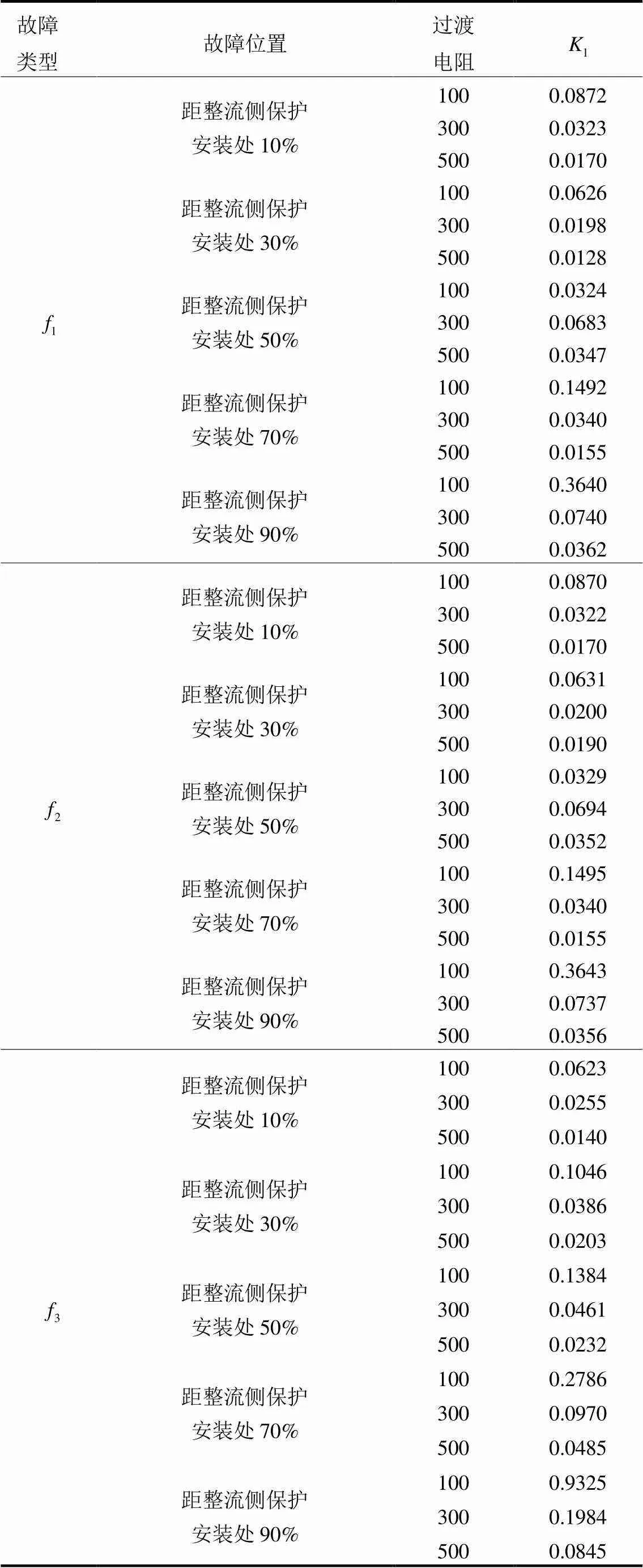
表2 区内高阻接地故障识别结果

表3 故障极识别结果

5.3 故障仿真验证结果

根据5.1节与5.2节可以得到故障后保护动作情况。由表4可知，当发生区内正极故障时，仅正极的保护元件动作；当发生区内负极故障时，仅负极的保护元件动作；当发生区内双极故障时，两极的保护元件均动作；而发生区外故障时，保护元件不动作。

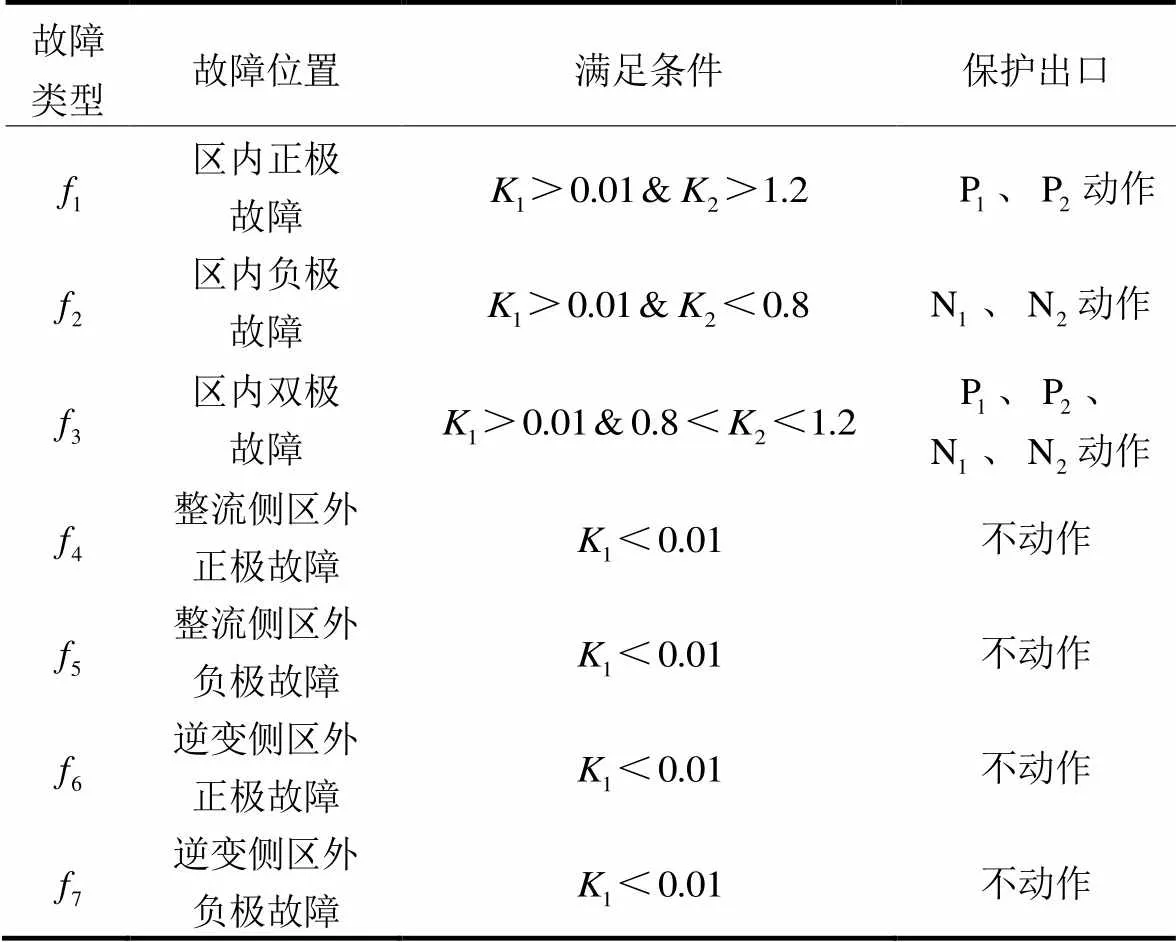
表4 故障仿真动作情况

6 结论

本文利用混合双端直流输电系统的边界特性，构造了一种基于VMD能量熵的直流线路纵联保护方法。通过PSCAD/EMTDC仿真平台搭建混合双端直流输电模型，通过模拟不同工况下的故障，提取电压信号，进行VMD分解，得到能量熵。利用能量熵区分区内外故障和故障极。经分析可得结论如下。

1) 在发生故障时，由于边界元件的存在，线路暂态电压骤变，且故障线路提取的电压故障分量变化量明显大于非故障线路，此特性可用于构造保护方法。

2) 当系统发生区内外故障时，所提取的电压故障分量的能量熵不同，可准确判定区内外故障，并利用同一侧换流站正负极能量熵之比进行故障极识别。

3) 此方法可准确保护直流线路全长。

4) 此方法可在过渡电阻为500 Ω时准确识别故障，具有较高耐高阻能力，可在3 ms内快速识别故障并可靠动作。

综上可知，本文所提的纵联保护方法易于实现，可靠性高，适应性强，具有较高精度，可准确识别故障。

[1] 李旭旻, 顾丹珍, 杨秀, 等. Statcom 对多馈入直流输电系统换相失败恢复过程的影响[J]. 电测与仪表, 2020, 57(13): 55-60.

LI Xumin, GU Danzhen, YANG Xiu, et al. Effect of Statcom on recovery process of commutation failure in multi-infeed HVDC system[J]. Electrical Measurement & Instrumentation, 2020, 57(13): 55-60.

[2] 韩伟, 孟沛彧, 刘超, 等. 高压直流输电系统接入下的交流系统不对称故障下序网等值及短路电流算法[J]. 电测与仪表, 2020, 57(23): 38-46.

HAN Wei, MENG Peiyu, LIU Chao, et al. Sequence network equivalence and short-circuit current algorithms for asymmetric faults of AC systems with HVDC connection[J]. Electrical Measurement & Instrumentation, 2020, 57(23): 38-46.

[3] 宋国兵, 高淑萍, 蔡新雷, 等. 高压直流输电线路继电保护技术综述[J]. 电力系统自动化, 2012, 36(22): 123-129.

SONG Guobing, GAO Shuping, CAI Xinlei, et al. Survey of relay protection technology for HVDC transmission lines[J]. Automation of Electric Power Systems, 2012, 36(22): 123-129.

[4] 杨洋, 王瑶, 李浩涛, 等. 子模块混合型LCC-MMC混合直流输电系统的启动控制策略[J]. 电力系统保护与控制, 2018, 46(8): 58-64.

YANG Yang, WANG Yao, LI Haotao, et al. Start-up control strategies for the cell-hybrid LCC-MMC hybrid HVDC system[J]. Power System Protection and Control, 2018, 46(8): 58-64.

[5] MUNIAPPAN M. A comprehensive review of DC fault protection methods in HVDC transmission systems[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 1-20.

[6] 唐庚, 徐政, 薛英林. LCC-MMC混合高压直流输电系统[J]. 电工技术学报, 2013, 28(10): 301-310.

TANG Geng, XU Zheng, XUE Yinglin. A LCC-MMC hybrid HVDC transmission system[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 301-310.

[7] 李少华, 王秀丽, 李泰, 等. 混合式MMC及其直流故障穿越策略优化[J]. 中国电机工程学报, 2016, 36(7):1849-1858.

LI Shaohua, WANG Xiuli, LI Tai, et al. Optimal design for hybrid MMC and its DC fault ride-through strategy[J]. Proceedings of the CSEE, 2016, 36(7): 1849-1858.

[8] CHU Xu. Unbalanced current analysis and novel differential protection for HVDC transmission lines based on the distributed parameter model[J]. Electric Power Systems Research, 2019, 171: 105-115.

[9] GAO Shuping, CHU Xu, SHEN Quanyu, et al. A novel whole-line quick-action protection principle for HVDC transmission lines using one-end voltage[J]. International Journal of Electrical Power and Energy Systems, 2015, 65: 262-270.

[10] SONG Guobing, CHU Xu, GAO Shuping, et al. A new whole-line quick-action protection principle for HVDC transmission lines using one-end current[J]. IEEE Transactions on Power Delivery, 2015, 30(2): 599-607.

[11] 许小雪, 刘建锋, 江玉蓉. 基于多频带能量的高压直流输电线路单端暂态电流保护[J]. 电力系统保护与控制, 2016, 44(22): 32-39.

XU Xiaoxue, LIU Jianfeng, JIANG Yurong. HVDC transmission line protection based on single-ended transient current using multiband energy[J]. Power System Protection and Control, 2016, 44(22): 32-39.

[12] 高淑萍, 叶换飞, 宋国兵. 一种±500 kV混合双极高压直流输电线路保护的新方法[J]. 西安交通大学学报, 2020, 54(6): 36-43.

GAO Shuping, YE Huanfei, SONG Guobing. New protection method of ±500 kV hybrid bipolar high-voltage DC transmission line[J]. Journal of Xi'an Jiaotong University, 2020, 54(6): 36-43.

[13] 张大海, 杨宇辰, 刘艳梅, 等. 基于EMD与Spearman相关系数的混合直流线路纵联保护方法[J]. 电力系统保护与控制, 2021, 49(9): 1-11.

ZHANG Dahai, YANG Yuchen, LIU Yanmei, et al. Hybrid HVDC line pilot protection method based on EMD and Spearman correlation coefficient[J]. Power System Protection and Control, 2021, 49(9): 1-11.

[14] 高淑萍, 张楚, 宋国兵, 等. 一种混合双端直流输电线路暂态保护方案[J]. 科学技术与工程, 2020, 20(24): 9911-9917.

GAO Shuping, ZHANG Chu, SONG Guobing, et al. A transient protection for hybrid double-ended direct current transmission line[J]. Science Technology and Engineering, 2020, 20(24): 9911-9917.

[15] 田书, 康智慧. 基于改进变分模态分解和SVM的断路器机械故障振动分析[J]. 振动与冲击, 2019, 38(23): 90-95.

TIAN Shu, KANG Zhihui. Circuit breaker mechanical fault vibration analysis based on improved variational mode decomposition and SVM[J]. Journal of Vibration and Shock, 2019, 38(23): 90-95.

[16] 李永刚, 丁其, 赵书涛. 基于变分模态分解的断路器机械故障诊断[J]. 电测与仪表, 2019, 56(20): 82-86.

LI Yonggang, DING Qi, ZHAO Shutao. Circuit breaker mechanical fault diagnosis based on variational mode decomposition[J]. Electrical Measurement & Instrumentation, 2019, 56(20): 82-86.

[17] 贾亚飞, 朱永利, 王刘旺, 等. 基于VMD和多尺度熵的变压器内绝缘局部放电信号特征提取及分类[J]. 电工技术学报, 2016, 31(19): 208-217.

JIA Yafei, ZHU Yongli, WANG Liuwang, et al. Feature extraction and classification on partial discharge signals of power transformers based on VMD and multiscale entropy[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 208-217.

[18] 朱永利, 贾亚飞, 王刘旺, 等. 基于改进变分模态分解和Hilbert变换的变压器局部放电信号特征提取及分类[J]. 电工技术学报, 2017, 32(9): 221-235.

ZHU Yongli, JIA Yafei, WANG Liuwang, et al. Feature extraction and classification on partial discharge signals of power transformers based on improved variational mode decomposition and Hilbert transform[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 221-235.

[19] 谢李为, 曾祥君, 柳祎璇. 基于VMD-Hilbert变换的故障行波定位研究[J]. 电力系统保护与控制, 2018, 46(16): 76-81.

XIE Liwei, ZENG Xiangjun, LIU Yixuan. Research on fault traveling wave location based on VMD-Hilbert transform[J]. Power System Protection and Control, 2018, 46(16): 76-81.

[20] 付华, 王婧羽. 基于SR-VMD的微弱故障行波检测方法[J]. 电力系统保护与控制, 2021, 49(1): 156-162.

FU Hua, WANG Jingyu. Weak fault traveling wave detection method based on SR-VMD[J]. Power System Protection and Control, 2021, 49(1): 156-162.

[21] 付华, 吴赛, 徐耀松, 等. 基于VMD与广义S变换的HVDC线路故障定位[J]. 电力系统保护与控制, 2020, 48(4): 125-133.

FU Hua, WU Sai, XU Yaosong, et al. HVDC line fault location based on VMD and generalized S-transform[J]. Power System Protection and Control, 2020, 48(4): 125-133.

[22] 黄传金, 周铜. 基于变分模态分解的电能质量扰动检测新方法[J]. 电力自动化设备, 2018, 38(3): 116-123.

HUANG Chuanjin, ZHOU Tong. A new detection method of power quality disturbance based on VMD[J]. Electric Power Automation Equipment, 2018, 38(3): 116-123.

[23] 赵碗君. 高压直流输变电工程技术[M]. 北京: 中国电力出版社, 2010.

[24] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.

Longitudinal protection scheme of hybrid double-terminal DC transmission lines based on VMD energy entropy

GAO Shuping1, SONG Xiaochen1, SONG Guobing2

(1. College of Electrical and Control Engineering, Xi'an University of Science and Technology, Xi'an 710054, China;2. School of Electrical Engineering, Xi'an Jiaotong University, Xi'an 710049, China)

To improve the quick fault clearing ability of hybrid dual-terminal HVDC transmission lines and ensure the safe operation of the transmission system, a hybrid dual-terminal HVDC transmission line longitudinal protection method based on variational mode decomposition energy entropy is proposed. Given the different voltage energy on both sides of HVDC boundary elements, and considering the fault types and the influence of transition resistance, a protection scheme of energy entropy of the voltage fault component is constructed.The voltage fault components are collected at measurement points when faults are decomposed by VMD to obtain some inherent modal components and calculate the energy entropy. The fault criteria are constructed according to the values of energy entropy of the voltage fault components in and out of the zone, and a fault pole criterion is constructed according to the ratio of the energy entropy of the components in and out of the zone. The method is verified usingPSCAD/EMTDC modeling and simulation, Matlab and protection criteria. The results show that the protection method is fast, and has high reliability and strong resistance to transition resistance.

hybrid double-ended DC transmission system; relay protection; fault; variational mode decomposition; energy entropy

10.19783/j.cnki.pspc.211115

国家自然科学基金面上项目资助(51777166)；国家自然科学基金联合基金重点支持项目资助(U1766209)；中国国家留学基金项目资助

This work is supported by the General Program of National Natural Science Foundation of China (No. 51777166).

2021-08-17；

2021-12-13

高淑萍(1970—)，女，通信作者，博士，副教授，研究方向为高压直流输电线路保护与故障定位、新能源并网关键技术、直流配电网的保护等；E-mail: gao.sp2003@163.com

宋晓辰(1997—)，女，硕士研究生，研究方向为高压直流输电线路保护与故障定位。E-mail: 1622176893@qq.com

(编辑 许 威)