基于教材原题的一题一课探究
——以“圆周角”专题课教学为例
2022-08-05武汉市恒大城学校王华峰
武汉市恒大城学校 王华峰
武汉市东西湖初级中学 封 磊
1 一题一课,忠于教材
1.1 “一题一课”的重要意义
教师在义务阶段的数学教学中,要尤其注重学生数学思维的养成[1].数学是一门抽象的学科,仅仅让学生执行题海战术远远不够,题型稍微变化对于学生而言又是一个崭新未接触过的“领域”,从而会出现即使做过也没有思路的现象.作为义务阶段教师,可通过“一题一课”的方式来帮助学生整理并归纳知识点,通过适量的类比性练习让学生学会解决同类型问题.与此同时,“一题一课”的练习更是为了锻炼学生举一反三的能力,提升学生的思维,拓宽学生的能力.
下面以人教版九年级上学期“圆周角”专题课教学为例进行说明.
1.2 “一题一课”立足于教材
“一题一课”并非一道题讲一节课,而是立足于教材本身,以教材母题为载体,通过适当改变题目条件,围绕本节习题课“平分圆周角”的知识点,发挥整理与归纳的重大作用.九年级学生基本具备独立思考的能力,所以教师更应该立足于教材,通过“一题一课”这种形式让学生最大程度落实与掌握教材中的单一知识点.
2 试题之源,源于教材
(人教版九年级上学期数学教材第90页第14题)如图1,A,P,B,C是圆O上的四个点,∠APC=∠CPB=60°,判断△ABC的形状?并证明你的结论.
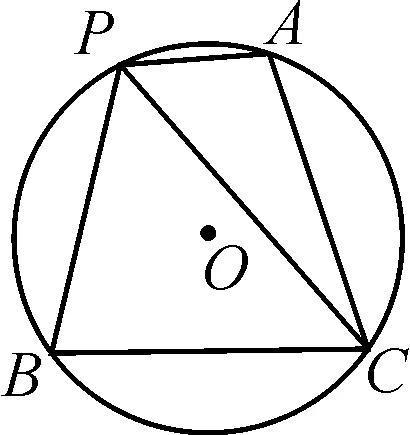
图1
师:同学们,我们知道顶点在圆上,且两条边都与圆相交的角为圆周角.请同学们回顾圆心角、圆周角、弦三者之间的关系?
生:同圆或等圆中,等弧所对的圆周角是圆心角的一半;同圆或等圆中,相等的弦所对的劣弧相等.
师:是的.请同学们先独立解决课本中的题,思考解题过程中运用了圆的哪些相关性质?
生:△ABC为等边三角形.运用了在同圆或等圆中,相等的圆周角所对的弦相等;还运用了圆的内接四边形对角互补.
师:回答得很好.由题目所给的条件∠APC=∠CPB=60°,细心的同学可以发现,线段PC为圆周角∠APB的角平分线.那么老师将本题追加一个课堂活动:分小组一起探讨线段PA,PB,PC三者之间的数量关系.
设计意义:让学生对所学的性质进行简单的梳理,并在解题过程中及时巩固所学过的知识点.在教材练习题基础上,增设课堂活动,鼓励学生独立或以小组合作的形式探讨,加深对本题的理解,同时锻炼发散性思维.
3 题型之变,变于教材
3.1 学生寻解题之路,教师展学习之法
在分组谈论的过程中,其中几个小组的学生分别运用不同的方法解决了线段PA,PB,PC数量关系问题,但也有个别小组没有思路.此时,教师应该让学生畅谈自己的想法,展现小组合作的成果.待学生展示完毕,教师再引导学生作出归纳并总结.
生:如图2,将△APC绕点A顺时针旋转60°至△AQB,因为△ABC为等边三角形,所以点C旋转后与点B重合,△AQP为等边三角形,于是PA=PQ.因为PC=QB,QB=QP+PB,所以PC=PA+PB.
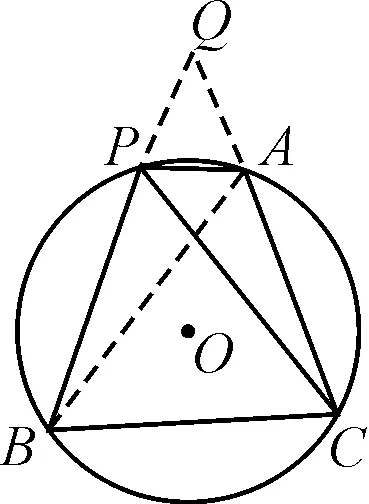
图2
师生反馈评价:回答问题的学生思路方向是正确的,但解题过程中忽视了某个知识点的细节,从而解法存在问题.在运用旋转思想解题的时候,如何保证三点共线呢?在整个思路中,△APC绕点A顺时针旋转60°时,因为△ABC为等边三角形,所以点C恰好与点B重合.又因为∠PAQ=60°,PA=QA,所以△PQA为等边三角形,从而∠QPA=60°,所以∠QPB=∠QPA+∠APB=180°,那么点Q,P,B三点共线.
旋转思想在几何题的计算与证明中大有用处,为了锻炼学生的思维能力并巩固所学的知识点,尝试探讨是否有其他解法.在探讨的过程当中时刻关注学生存在的问题,并引导学生独立解决.如图3,在弦PC上取一点G,使PG=PB,连接BA,BG.因为∠GPB=60°,所以△PBG为等边三角形,故PB=GB.因为∠PBA+∠ABG=60°,∠GBC+∠ABG=60°,便可以得到∠PBA=∠GBC.又因为∠BGC=180°-∠PGB=180°-60°=120°,∠BPA=120°,所以∠BGC=∠BPA,从而得到△BPA≌△BGC.进一步得到PA=GC,PC=PG+GC=PB+PA.
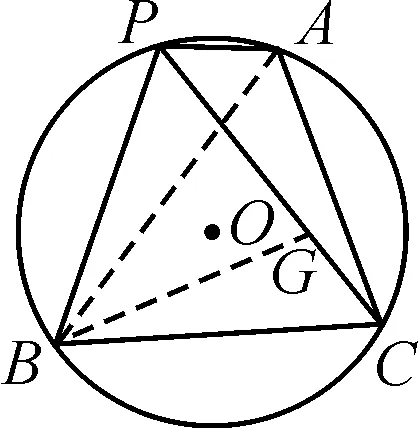
图3
点评:本题探讨了在圆中平分120°圆周角的角平分线所具有的一些性质.两种不同的思路与方法诠释了解题的过程.在运用旋转思想解题时,需要证明点的共线.用第二种方法截取线段长相等来考虑时,就必须观察图中有哪些三角形是全等的.
3.2 原题重现,并非偶然
例1(2021-2022学年武汉市元月调考第20题)如图4,A,P,B,C是⊙O上的四点,∠APC=∠CPB=60°.(1)判断△ABC的形状,并证明你的结论;(2)求证:PA+PB=PC.
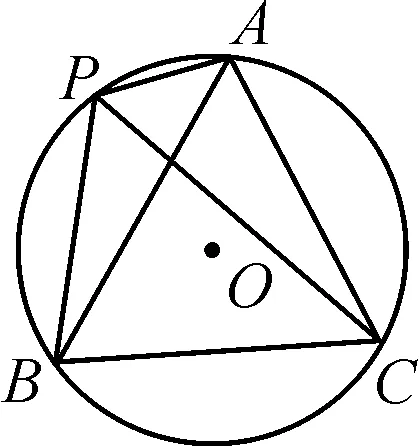
图4
分析:本题第(1)(2)两问不难看出就是人教版九年级上学期数学教材中的第90页第14题,并且在上述讨论中提供了两种不同的解法.教师还可以循循善诱,反问学生既然我们可以在弦PC上取一点G,使PG=PB,那么,我们是否也同样可以在弦PC上取一点M,使PM=PA呢?解法和上述的方法异曲同工.
3.3 深化巩固,环环紧扣教材
元月调考试题源于教材,这可能是一个命题趋势,所以在平时的学习过程当中更应该注重教材的使用.在课堂教学与课后练习中,帮助学生适量地刷题,不能盲目地执行题海战术.引导学生共同探讨课本中的题型可以做何种变式,让学生自己尝试在教材母体基础上改编,最大限度地发挥学生的主体思维,让学生在做题的同时领悟题型的变化.
师:目前讨论的是平分120°的圆周角所具有的一些性质,请同学们共同探讨,还可以平分多少度的圆周角呢?
生:90°,60°.
师:请同学们分为两个小组,分别探讨平分90°圆周角和平分60°圆周角的相关性质与结论.
变式1如图5,若把上述条件∠APB=120°改为∠APB=90°,其余条件不变,试判断△ABC的形状?线段PA,PB,PC三者的数量关系?

图5
解析:△ABC为等腰直角三角形.如图6,将△CAP绕点C顺时针旋转90°至△CBN.

图6
∵△ABC为等腰直角三角形,AC=BC,
∴点A旋转后与点B重合.
∵四边形PACB为圆O内接四边形,
∴∠PAC+∠PBC=180°.
∵∠PAC=∠NBC,
∴∠NBC+∠PBC=180°,
∴P,B,N三点共线.
又∵△PCN为等腰直角三角形,
∵PN=PB+BN=PB+PA,
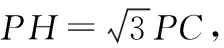

图7

3.4 中考真题再现
变式2(武汉中考)如图8,⊙O的直径AB的长为10,弦AC的长为6,∠ACB的平分线交⊙O于点D,求CD的长.

图8
分析:观察圆周角∠ACB=90°时,CD为∠ACB的角平分线,可运用上述方法来求解.
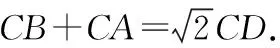
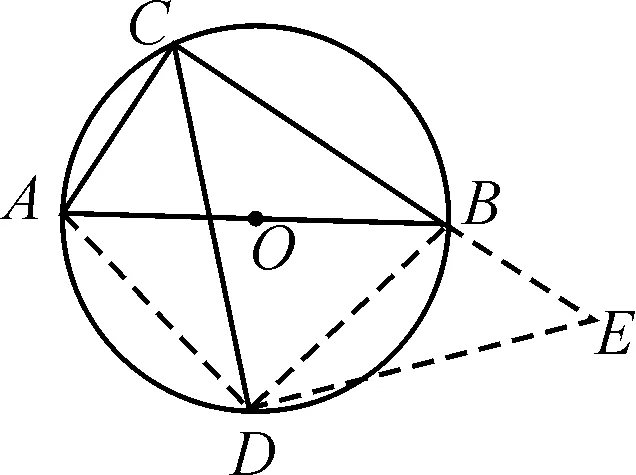
图9


图10
3.5 真题引申,发散性解题
变式3在变式2的基础上对试题进行相应的变化,能否求解出变式2中圆内接四边形CADB的面积?

4 教学思考
本课题以人教版九年级上学期数学教材原题作为模板,以一题一课[2]的形式逐渐展开,研究并探讨了武汉市元月调考真题到武汉市中考真题.整节专题课的设计,在问题呈现上从封闭式转为开放式旨在促使学生对特殊圆周角角平分线性质的掌握.在师生互动和学生分组讨论的过程中,学生有能力自己解决的问题交给学生展示,能力范围外的,教师因势利导,引导他们发现题目的切入点.同时,精简课程的内容,避免大范围的题海战术,有助于学生掌握题目的内在规律,抓住问题的本质,忠于教材.本节课更加注重圆周角问题中的几何模型,教师在日常教学中应指导学生构造基本模型,让学生在原有的认知上持续锻炼概括与总结能力,对知识体系的形成有很大的帮助.
