薄砂岩储层内部不连续性检测技术

肖 湘,尹 成,彭 达,丁 峰,张 栋

(1.西南石油大学地球科学与技术学院,四川成都 610500;2.中国石油西南油气田公司勘探开发研究院,四川成都 610041)

在河流相和三角洲相砂岩储集体中,发育有叠置的复合砂体,其内部结构的纵、横向变化通常对流体具有明显的阻隔和控制作用,造成砂岩储层非均质性增强[1-2]。随着油气勘探开发的深入,为了给油田提高采收率、部署调整井等工作提供决策参考,获取更薄或更小层级砂岩储层内部的不连续性信息并识别影响流体的结构,成为储层不连续性研究的重要方向之一。

目前用于储层不连续性检测的技术大多源自识别断层和其它显著不连续性地质结构的方法,包括相干类地震属性结合蚂蚁追踪这样的组合技术也是如此。相干类地震属性算法最早由BAHORICH和FARMER于1995年提出,该方法利用3道地震数据中的滑动时窗计算出最大互相关,然后测量局部波形的相似性,通过低相似性波形与断层等结构的对应关系,使不连续的部分从地震数据中突显出来[3-4]。之后,各种地震属性方法被不断提出或改进,包括由梯度结构张量建立的相干属性[5]、局部结构熵[6]、倾角导向梯度能量熵[7]、最大似然属性[8]方法等。上述方法通过测量地震数据中局部信息的相似性或差异性,来突出断层特征在地震数据体中的位置,并且对于识别某些显著的地层、岩性变化也具有一定的效果。在实际应用过程中,由于这些属性会不可避免地受到原始地震数据中噪声的影响,造成目标特征模糊不清,为了更好地实现断层自动识别等后续操作,蚂蚁追踪(ant tracking)方法被引入商业软件中[9]。在优化此类使用蚁群算法基本思想的方法技术时,严哲等[10]提出方向约束蚁群算法,通过对提取的相干类属性进行处理来实现增强断层响应,提升断层的可追踪性,进一步提高了蚁群算法在断层自动追踪流程中的效果;马艺璇等[11]对蚂蚁追踪的输入数据体进行匹配追踪频谱分解和二次去噪,并结合测井资料反复调整追踪参数,在实际地震资料处理中提升了对不同尺度断裂的刻画效果。对于薄砂岩储层内部通常存在的一些不连续性结构,由于其尺度通常接近或小于1/4地震波长,因此在反射旅行时、地震振幅或波形等方面的差异变化不够明显,导致常规相干类方法对其产生的响应偏弱,不连续性特征难以被准确识别解释。同样,由于薄砂岩储层内部不连续性结构的响应相对偏弱,这些结构在长度和形态等方面与断层等不连续性结构存在一定差异,故采用基于蚁群的常规算法增强此类不连续性特征的效果不明显,且不能满足对薄砂岩储层进行更精细刻画的需求。

为了提高对薄砂岩储层内部不连续性结构的识别能力,本文在充分认识地震属性对地下岩性构造变化响应优势的基础上,首先介绍了灰度共生矩阵均质性计算方法,并利用均质性从属性数据中初步提取不连续性信息;然后提出了路径弯曲度约束蚁群算法,用于进一步增强不连续性特征;最后将该技术应用于模型数据和实际工区资料的储层内部不连续性检测,验证了组合技术的有效性。

1 方法原理

从地震属性与地震数据的关系来看,地震属性可以视作是原始地震数据中全部信息的一个子集[12]。从原始地震数据到地震属性数据,不同地质信息在数据中的占比会发生改变,这使得特定的地质特征在某些地震属性中引起的变化往往比在地震数据中更加明显。前人针对河流相和三角洲相不同复合砂体构型样式进行的正演模拟显示,地下沉积体的变化会引起地震波形、频率和振幅等变化,上述变化可通过相应类型的敏感属性实现构型的识别和区分[13-14]。在单砂体楔形模型以及薄互层砂体的相关研究中,当砂岩厚度小于1/4地震波长时,地震振幅随厚度变化的程度比全信息的地震数据随厚度变化的程度更加明显[15-16]。因此从地震数据中提取的振幅属性数据能用于定位砂体边缘以及复合砂体内部砂体叠置等不连续性结构的信息占比更高。考虑到算法的稳定性、原始数据的噪声以及层位解释的小瑕疵等对属性计算结果的影响程度,均方根振幅属性可以作为灰度共生矩阵均质性计算的输入数据,其属性值变化与砂岩厚度改变位置具有较强的相关性,可以反映叠置砂岩的平面分布特征[17]。因此,本文提出的检测薄砂岩储层不连续性的流程主要包括:①对目标层位提取的地震均方根振幅属性;②计算其灰度共生矩阵的均质性统计量;③利用改进后的蚁群算法对均质性数据进行增强;④获得不连续性特征结果。

1.1 灰度共生矩阵均质性计算

灰度共生矩阵的均质性是衡量图像纹理均匀程度或像素间相似性的统计量[18],均质性计算结果可以突出相邻道属性值的微小变化。基于数值为有理数的均方根振幅属性生成灰度共生矩阵,首先需要将均方根振幅属性值转化为灰阶图像,转化公式如下:

(1)

式中:a是某点属性值;amin和amax是属性的最小值和最大值;G是转化时设定的最大灰阶数;Int()是取整;Ng是a的转化结果。

采用上述公式进行数据转化后,可将其结果视作二维图像来生成灰度共生矩阵并计算其均质性参数[19]。灰度共生矩阵定义如下:位于Wx×Wy范围内相隔距离为δ、连线方向为θ的两个像素,灰度分别为i和j的情况的发生率P所构成的矩阵。若以(x1,y1)和(x2,y2)表示距离为δ、连线方向为θ的两个像素坐标,则将P记为:

P(i,j,δ,θ)=c{[(x1,y1),(x2,y2)]∈(Wx×

Wy)×(Wx×Wy)|g(x1,y1)=i,g(x2,y2)=j}

(2)

式中:c{}表示满足条件的元素个数;g(x,y)表示范围Wx×Wy内像素(x,y)的灰度值。

在地震勘探领域,通常设定δ=1以保证相邻道连续性,θ分别取4个方向的值[20]。在给定δ和θ的情况下,像素两两之间构成点对的总数为R,P(i,j,δ,θ)可以简化表示为Pi,j,由该元素构成的灰度共生矩阵M归一化表达为:

(3)

以图1红框所示的3×3范围为例,当θ=0时,灰度值为7和10的像素点对只有一个,所以P7,10=P10,7=1。而在(3)式中,当θ为0°或者90°时,则R=2×Wx×(Wy-1);当θ为45°或135°时,则R=2×(Wx-1)×(Wy-1)。

图1 灰度共生矩阵的方向

得到灰度共生矩阵后,均质性H的计算公式为:

(4)

将不同方向的灰度共生矩阵均质性值取平均,得到最终的计算结果。较低的均质性代表着非零元素分散在灰度共生矩阵中,指示分析窗位置存在着能引起地震属性变化的不连续性结构。灰度共生矩阵的灰阶数G以及Wx和Wy的选取,也影响着均质性结果对隐蔽不连续性信息的刻画能力以及不连续性特征边缘的分辨能力。以图2a中红线勾勒的不连续性结构为例,在图2b中设定G为64阶,当Wx和Wy取值均为3时,均质性结果能清晰显示均方根振幅异常宽度约为6的隐蔽不连续性结构边缘,而当Wx和Wy同时为7时,该隐蔽结构难以识别,同时我们难以准确分辨属性图上更明显的不连续性特征的边缘。因此,Wx和Wy取值应该为目标不连续性特征尺度的一半,过大会造成不连续性结构形态无法识别,过小则会导致细小干扰信息影响显示效果,Wx和Wy为3时,目标结构的边缘刻画结果较为理想。如图2c 所示,设定Wx×Wy为3×3,当灰阶数从8阶增大到64阶时,不难发现,利用均质性结果可以更好地突出该隐蔽不连续性结构,从64阶进一步增大到128阶后,不难发现,利用均质性结果进行识别,提升效果不明显,计算量和其它干扰信息增多。因此,在灰阶数刚好满足目标特征且目标结构被准确刻画后,再将值提高约1/3使目标进一步突出,则识别效果更为理想,G大于32阶接近64阶时,识别效果最佳。

图2 不同参数计算灰度共生矩阵均质性效果a 原始均方根振幅属性; b 灰阶数G=64,不同Wx×Wy; c Wx×Wy为3×3,不同灰阶数G

1.2 路径弯曲度约束的蚁群算法

由地震属性得到的均质性计算结果不可避免地含有原始数据中的随机噪声,容易造成不连续性特征模糊。为了改善不连续性特征的显示效果,采用路径弯曲度约束蚁群算法对均质性计算结果进行增强。

蚁群算法的灵感来源于蚂蚁们寻找最短觅食路径的机制,该算法可用于解决某些优化问题,其基本要素通常包括信息素的激励和挥发、终止条件、转移规则和移动代价等[21]。通过蚁群算法来突出不连续性特征、改善断层特征连续性和压制噪声,利用的就是人工蚂蚁倾向于但不限于朝信息素浓度高的方向移动,移动过程包括根据移动距离在路径上留下相应浓度信息素的正反馈过程以及旧信息素不断挥发的过程等。

蚁群增强算法的第1步:将均质性平面数据分割为由N×N个数据点组成的区域,并在每一个区域中投入1只蚂蚁。根据如下的概率公式蚂蚁选择区域内坐标为(r,s)的点作为起始点:

(5)

式中:H(r,s)表示坐标为(r,s)的点的均质性值,为归一化的数值。

蚁群增强算法的第2步:计算蚂蚁从坐标为(r,s)的点到下一个坐标为(i,j)的点转移概率,计算公式为:

(6)

式中:Ω(r,s)包含蚂蚁从坐标为(r,s)的点可以选择的所有转移候选点;τ(i,j)是坐标为(i,j)的点的信息素浓度;α和β是定值,用于控制信息素和启发函数η(i,j)对转移概率的影响;(u,v)为Ω(r,s)中的任意一点坐标。启发函数定义为:

η(i,j)=1-H(i,j)

(7)

对于剖面上的断层特征,可以依据其倾角对蚂蚁转移方向进行一定程度的约束,更好地增强区域内成组的断层线[22]。不同于断层线在剖面和平面上都具有一定延伸长度并且局部弯曲较少的特性,对于河流相和三角洲相薄层复合砂体内的不连续性结构,其垂向延伸长度通常在地层厚度以下,而不连续性特征形成的线或条带在沿层切片上弯曲转向更加显著且频繁。

因此,本文将断层追踪常用的方向约束条件修改为对路径弯曲度的约束[23],以适应薄层的不连续性特征,并防止蚂蚁在局部小区域形成转圈式的移动。在此约束条件下,Ω(r,s)中的点需要满足以下3个规则:①不包含在之前的移动路径中;②对于起始的第一步,蚂蚁选择的移动方向不受限制,而对非起始的一步,移动方向在上一步的基础上最大偏离限制在45°以内,当移动步长设定为1时,蚂蚁最多能选择3个点作为转移候选点;③满足规则①和②后,如果Ω(r,s)中仍含有类断层点,则只保留类断层点,将其它点从Ω(r,s)中剔除。

类断层点是通过一个预设的阈值F将某点与其它点进行区分。当该点均质性低于设定的F,表示该点很可能是不连续性特征上的一个点(虽然称为类断层点,在本文中这样的点包括但不限于断层特征上的点)。由于较小尺度的内部不连续性结构对均质性的反应相对不明显,因此为了增强这些不连续性特征,F需要尽可能地选择高值,也就是尽量多地将低均质性点归入类断层点。

以图3为例展示在路径弯曲度约束下,蚂蚁分别位于起始点和非起始点时,Ω(r,s)中转移候选点的情况。图3中绿色框表示该点是类断层点,黄色框表示该点不是类断层点,而红色框表示不可向该点移动,一般为该蚂蚁之前已经走过的点或没有均质性数据的点;黑色箭头指向可以转移的点。当坐标为(r,s)的点为起始点时(图3a),蚂蚁可以向周围8个方向移动,但可移动方向上存在类断层点时,禁止向非类断层点转移,所以黄色框的点不会包含在该Ω(r,s)中;如果坐标为(r,s)的点并非起始点(图3b),蚂蚁可移动方向受到上一步已移动方向的限制,所以Ω(r,s)中只包含箭头所指的3个点。因此,蚂蚁根据(6)式计算向Ω(r,s)中每个候选点转移的概率,然后蚂蚁根据候选点转移概率大小随机移动到候选点上,完成本次移动。

图3 转移候选点示例a 蚂蚁位于起始点时的转移候选点; b 蚂蚁在追踪过程中的转移候选点

如果Ω(r,s)为空,该蚂蚁直接终止移动;当Ω(r,s)中不存在类断层点时,蚂蚁有可能向非类断层点转移,这样的转移视作异常步。异常步数与正常步数的比例由终止条件S决定,其计算公式为:

(8)

式中:Smax和Smin是S的上限和下限,常用设置范围为0.1～0.5;D是此时Ω(r,s)内候选点均质性的平均值。当D比较高时,可能意味着蚂蚁移动远离了不连续性特征,此时允许的异常步变少,触发终止条件,蚂蚁移动迅速停止;反之,则会允许其多追踪几步来增强该特征的连续性[24]。提高Smin并推高Smax,能强制蚂蚁更多地向没有类断层点的区域探索,但也更容易导致结果中的不连续性特征以不符合地质规律的方式被连接起来,所以通常令Smax和Smin均为较小的值。如果因异常步数触发终止条件,则该蚂蚁将被放回上一个类断层点并终止移动。

蚁群增强算法的第3步:当所有蚂蚁都停止移动时,我们进入更新信息素的步骤。在当前迭代轮次,坐标为(i,j)的点信息素浓度定义为:

(9)

(10)

式中:c是信息素更新系数;L(k)是第k只蚂蚁走过路径的长度;Q是本轮次经过坐标为(i,j)的点的蚂蚁数量。考虑到薄储层中不连续性特征的长度与其重要性并无明显关系,为了防止蚂蚁向长度大的不连续性特征位置聚集,影响其它不连续性特征的增强,故设定信息素增量与蚂蚁经过路径长度呈对数关系,未使用蚂蚁追踪断层时信息素浓度随路径变长而线性增大的计算公式。

当信息素更新完成,该轮次迭代结束,蚂蚁最后停留的地方将作为下一轮迭代时移动的起点,并根据蚂蚁增强算法的第2步重复计算过程,直到迭代次数上限,最终得到的信息素浓度平面分布数据即为不连续性特征增强的结果输出,路径弯曲度约束蚁群算法的计算至此结束。

2 模型试验

为了检验上述组合技术检测薄砂岩储层内部不连续性的效果,使用图4a中所示的一个包含砂体侧向接触和断层的二维速度模型进行试算,两个结构分别代表了薄砂岩储层内部常见的、不同成因的小尺度不连续性结构。模型中砂岩厚度为19m,速度为3000m/s,围岩速度为2900m/s;断层两边砂岩层高差为9.3m,两个叠置砂体没有高差,砂体边缘侧向接触相切位置的最小厚度为12.3m。

图4b的地震剖面由图4a模型与30Hz的零相位雷克子波褶积生成,砂岩层厚度略小于调谐厚度。由于本文检测技术针对三维地震数据,因此将上述地震剖面复制63个构成一个三维数据体,然后以剖面中最强的波峰和波谷作为该砂岩层的顶层和底层,提取这两个层位间的均方根振幅属性,结果如图4c所示,可以看出,断层和砂体相切的不连续性结构均引起了均方根振幅属性值的变化。

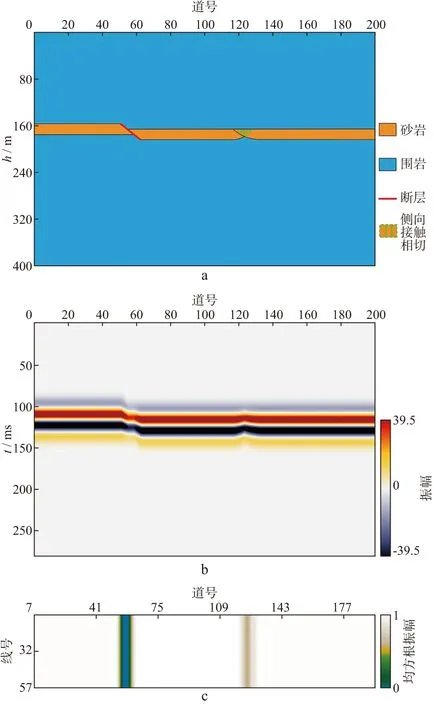
图4 不连续性检测方法的理论模型测试a 二维速度模型; b 合成的地震剖面; c 顶底层位时窗提取砂岩层均方根振幅属性

图5a为沿砂岩层位中间提取的局部结构熵体切片,图5b为对砂岩层均方根振幅属性计算得到的灰度共生矩阵均质性。对比图5a和图5b可以发现,无论是局部结构熵还是均质性,在断层位置都出现了明显的不连续性特征。在砂体相切的位置,局部结构熵的响应明显变弱,而从均质性结果中依然能看到明显的不连续性特征。从上述平面数据中各抽出一条In-line的数据,均都转化到0～1的区间,它们数值越接近1表示不连续性越高,越接近0表示不连续性越低,将转化后的地震数据绘制成曲线,结果如图5c所示。对局部结构熵而言,砂体相切的不连续性特征响应峰值约为断层响应峰值的26.83%,而其均质性约为断层响应峰值的96%。这表明在无噪声的理论模型中,采用本文方法得到的均质性结果能更好地突出薄层中隐蔽的不连续性结构。

图5 模型中砂岩层的不连续性特征提取a 局部结构熵体切片; b 灰度共生矩阵均质性; c 图5a和图5b两种结果响应的对比曲线

为了测试不连续性检测组合技术承受噪声干扰的能力,在模型的反射系数中加入了高斯随机噪声。其大小分别限制为原始最大反射系数的10%,15%和20%,获得的含噪地震数据体信噪比分别为12.56,9.04和6.52dB。图6为含噪地震数据体的地震剖面和砂岩层均方根振幅属性。

图6 含噪地震数据体的地震剖面和砂岩层均方根振幅层属性a 信噪比为12.56dB的地震数据体剖面; b 信噪比为12.56dB的地震数据体均方根振幅属性; c 信噪比为9.04dB的地震数据体剖面; d 信噪比为9.04dB的地震数据体均方根振幅属性; e 信噪比为6.52dB的地震数据体剖面; f 信噪比为6.52dB的地震数据体均方根振幅属性

图7为不同信噪比地震数据砂岩层位置计算得到的局部结构熵和采用本文方法计算得到的均方根振幅均质性。对比在断层和砂岩体相切处产生的两种不连续性特征,可以看出,无论在局部结构熵还是均方根振幅均质性沿层数据上,储层内部不连续性结构的响应受噪声影响严重。局部结构熵对模型断层位置指示拥有信噪比优势,根据均方根振幅均质性识别砂体相切位置的不连续性特征的效果更佳。从图7e可以看出,砂体相切位置的特征已经和噪声混在一起难以识别,而在图7f中该位置处,可以识别出一个较弱的条带状特征,更加接近该特征在无噪声时的形态。这表明对于含噪数据,采用本文组合技术得到的均方根振幅均质性结果仍能更好地保留微弱的不连续性信息。

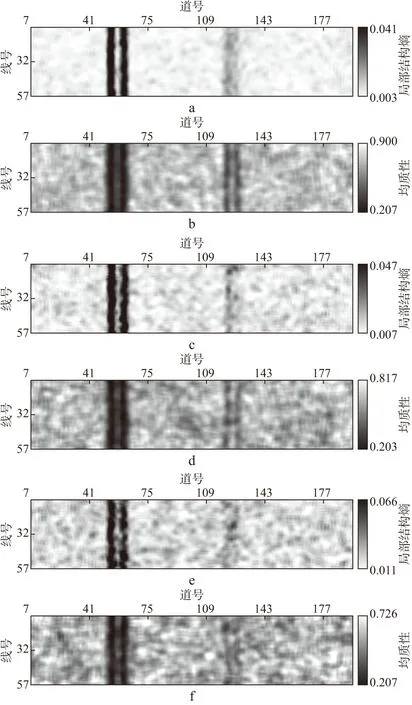
图7 不同信噪比数据砂岩层位置计算得到的局部结构熵和采用本文方法计算得到的均方根振幅均质性a 信噪比为12.56dB的地震数据体局部结构熵; b 信噪比为12.56dB的地震数据体均质性; c 信噪比为9.04dB的地震数据体局部结构熵; d 信噪比为9.04dB的地震数据体均质性; e 信噪比为6.52dB的地震数据体局部结构熵; f 信噪比为6.52dB的地震数据体均质性

对上面得到的不连续性特征数据进行增强,在砂岩层位置采用常规蚂蚁追踪优化后的局部结构熵体属性,将其与采用本文提出的路径弯曲度约束蚁群算法处理后的均方根振幅均质性进行对比。

从图8可以看出,采用常规的蚂蚁追踪和本文提出的路径弯曲度约束蚁群算法均可以有效压制不连续性识别中的干扰信息。应用于不连续性体属性的常规蚂蚁追踪更适合在三维空间中增强不连续性特征的曲面,在地震数据信噪比较高时,可以显著突出模型中砂体相切位置的响应(图8a);在信噪比下降后,只有断层位置的响应仍然明显,砂体相切位置的特征已经无法完整识别,并且还会出现许多由噪声引起的不连续性特征假象(图8e)。在均质性结果的信噪比降低后,采用路径弯曲度约束的蚁群算法还能相对较好地保持该不连续性结构的响应,并且不连续性特征的假象也明显较少(图8f)。

图8 采用常规蚂蚁追踪优化后局部结构熵与采用本文路径弯曲度约束蚁群算法处理后的均方根振幅均质性a 优化后信噪比为12.56dB的地震数据体局部结构熵; b 约束蚁群算法处理后信噪比为12.56dB的地震数据体均方根振幅均质性; c 优化后信噪比为9.04dB的地震数据体局部结构熵; d 约束蚁群算法处理后信噪比为9.04dB的地震数据体均方根振幅均质性; e 优化后信噪比为6.52dB的地震数据体局部结构熵; f 约束蚁群算法处理后信噪比为6.52dB的地震数据体均方根振幅均质性

本文提出的组合技术在无噪声和含噪声理论模型的测试结果表明,该组合技术可以检测薄砂岩层内部不连续性,并且还具有一定抗噪能力。相较于局部结构熵体属性加蚂蚁追踪优化的常规技术,本文提出的组合技术在识别小尺度不连续性结构的响应方面可以获得更好的效果。

3 实际数据应用

为了验证本文提出的检测不连续性的组合技术在实际地震数据处理中的可行性,选择渤海海上BZ油田的地震资料进行测试。该地震资料由高密度海底电缆采集,地震数据品质较好,主频约为43Hz,信噪比相对较高。地震数据覆盖区域内构造简单、断层少;目的层发育复合分流河道、朵体等沉积微相。储集体岩性以砂岩为主,井点钻遇砂岩的最大厚度与调谐厚度相近,其厚度较薄且横向变化较快,不同期次和微相的砂体接触与叠置关系复杂,导致储层非均质性强。因此,在实际工作中,砂体分布特征和内部结构是储层不连续性检测的重点环节。

图9a为工区目的层砂岩厚度预测结果,图中灰色表示该区域的一个已知断层,深蓝色虚线框内的砂岩为叠置的复合砂体,红色折线穿过断层和可能由叠置形成的不连续性结构,如图9b中绿色箭头所示,沿该折线的剖面如图9c所示,可以看出,断层位置同相轴的错动比砂体内不连续性结构位置的振幅变弱特征更易识别。

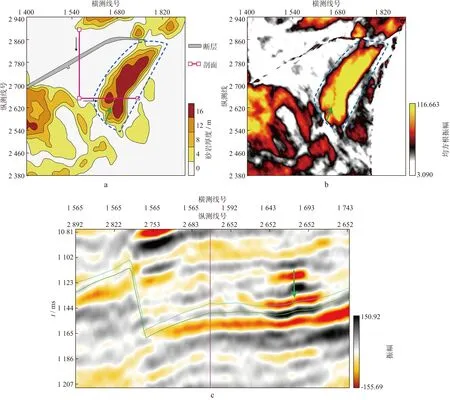
图9 工区目的层平面数据和地震数据剖面a 砂岩厚度预测结果; b 目的层均方根振幅; c 沿图9a红色折线形成的剖面

相较于根据地震数据计算得到局部结构熵属性沿目的层的切片(图10a),根据均方根振幅属性计算得到的灰度共生矩阵均质性切片(图10b),目标复合砂体的边缘更加清晰,在可能存在砂体重叠的位置能隐约识别出不连续性特征。

图10 目的层局部结构熵属性(a)和根据均方根振幅属性计算得到的灰度共生矩阵均质性(b)切片

在局部结构熵属性上使用常规蚂蚁追踪优化得到目的层切片数据(图11a),对目的层应用路径弯曲度约束的蚁群算法进行平面增强后的结果(图11b),可以看出两种不连续性特征优化算法对于实际数据噪声均具有良好的压制作用。受益于均质性结果的不连续性特征相对显著,在使用本文提出的路径弯曲度约束蚁群算法进行平面增强后,目标复合砂体无论是边缘还是内部的不连续性特征都更加突出。而作为对比的蚂蚁追踪结果,则因为局部结构熵对砂体边缘响应较弱,故将砂体范围内的不连续性特征与断层的特征错误连接起来造成了假象。

图11 对局部结构熵属性进行蚂蚁追踪优化得到的目的层切片(a)以及对目的层应用本文方法得到的平面增强结果切片(b)

将图11b获得的不连续性特征叠加到图9a所示砂岩厚度预测结果上,得到图12a所示的叠加显示结果。由叠加后的平面图分析可知,目标复合砂体可能由一个小砂体和一个大砂体的叠置相切形成,而通过不连续性特征约束砂体厚度预测结果,可以获得对目标砂体平面展布更精细的认识(图12b)。

图12 将不连续性特征应用于目标砂体得到的结果a 不连续性特征与砂体厚度预测结果叠加显示; b 不连续特征约束下的砂体预测厚度

由本文提出的检测不连续性的组合技术在实际地震数据的应用效果分析可知,该组合技术可以用于储层内部小尺度的不连续性结构检测,应用效果可靠,证明了技术的有效性。

4 结论

在河流相和三角洲相砂岩油气藏中,利用常规方法对薄砂岩储层不连续性结构进行识别,容易忽略一些小尺度结构,而对不连续性检测的各个步骤进行有针对性的综合改进,才能从现有的地震资料中提取到更多的不连续性信息,提升检测效果。本文利用均方根振幅属性,从地震数据中提取出与储层砂岩厚度变化以及砂岩展布关联性更强的信息,并利用对微弱变化更加敏感的灰度共生矩阵均质性,将提取出的信息转化为不连续性特征数据;然后根据薄砂岩储层平面数据上的不连续性特征展布特点,改造用于断层优化的蚁群算法,形成路径弯曲度约束的蚁群算法,使其能够适应目标特征,达到压制干扰和增强不连续性信息显示效果的目的。本文提出的薄砂岩储层内部不连续性检测的组合技术在模型和实际地震数据应用的结果表明,相较常规不连续性体属性和蚂蚁追踪组合技术,本文组合技术能取得更好的效果,成果可以用于辅助砂体厚度的预测,并且在此基础上能增进对复合砂体内部结构的认识。需要指出的是,本文方法受限于地震资料品质条件,检测效果可能存在差异,在使用信噪比更低的地震资料识别不连续性结构时,可能还需要选择合适的滤波算法进行预处理。