基于多尺度信号调节自编码器的永磁电机故障诊断研究

汪文龙， 贺长波， 王骁贤， 陆思良

(1.安徽大学 电气工程与自动化学院 高节能电机及控制技术国家地方联合工程实验室，合肥 230601；2.中国科学技术大学 精密机械与精密仪器系，合肥 230027)

永磁电机以其高效率、高功率密度、低噪音等独特优点在工业自动化和电动汽车中得到了广泛应用。电动机在长时间转动后会发生故障。典型的电机故障类型包括机械故障、电气故障和磁类故障。轻微的故障会引起额外的热量、振动和噪音，严重的故障会导致电机过热甚至起火。因此电机状态监测和故障诊断是保证电机安全运行的关键。

电机故障诊断包括信号采集、特征提取和模式识别3个连续的步骤。在第一步中，从加速度计、电流电压传感器和温度传感器等获取反映电机状态的信号，利用信号处理方法和统计方法提取故障相关特征。最后，可以采用多种基于机器学习的分类器对电机故障类型进行分类。

近年来，深度神经网络(deep neural networks, DNNs)在故障诊断和预测方面被广泛研究应用[1-6]。DNNs自动从监测信号中提取多层次特征，无需传统方法对敏感特征的选择过程。例如，胡晓依等[7]将卷积神经网络结合支持向量机搭建适于轴承故障诊断的深度卷积神经网络模型。赵春华等[8]提出了一种基于深度学习特征提取、鲸鱼优化算法及支持向量机状态识别相结合的故障诊断模型。杨平等[9]提出一种基于卷积胶囊网络的故障诊断方法，该模型使用两个卷积层的卷积网络直接对原始的一维时域信号进行特征提取,并将其送入胶囊网络,输出每种故障类型的诊断结果。Hoang等[10]将轴承一维振动信号转换成二维灰度图作为模型的输入应用于轴承故障模式的自动识别。Lei等[11]利用长短期记忆(long short term memory,LSTM)网络有记忆时序数据信号的优势，提出一种基于LSTM的故障诊断模型，并在风力涡轮机数据集上验证了该模型的有效性。

为了直接从原始信号中学习故障特征，国内外学者提出了多种自编码器网络实现故障诊断和分类。例如，李晴晴等[12]提出一种基于改进堆叠自编码器的故障诊断方法，该方法基于改进的dropout技术构建分类深度自编码网络模型。徐活耀等[13]提出一种基于堆栈稀疏自编码器和softmax层构建的深度神经网络用于轴承故障诊断。陈仁祥等[14]利用栈式稀疏加噪自编码深度神经网络进行了滚动轴承损伤程度诊断。罗金等[15]将总体平均经验模态分解和堆叠稀疏自编码网络结合，在准确性和训练时长上有一定的优势。为提高堆叠稀疏降噪自编码器的性能，解决其计算复杂度高、收敛速度慢等问题，张智恒等[16]提出了一种基于堆叠边缘化稀疏降噪自编码器的滚动轴承故障诊断方法。

以上方法对于识别特定工况下的机械故障表现出了较好的效果。然而，在实际应用中，信号往往受到强背景噪声的干扰，从而影响了特征提取和降低故障模式识别的精度。针对强噪声背景下滚动轴承故障诊断的困难，杨建华等[17]提出了一种基于级联自适应分段线性随机共振系统降噪的经验模态分解方法。徐元博等[18]引入一种新的轴承故障特征提取方法，首先利用变分模态分解算法先将故障信号分解为若干个成分单一的模态分量，然后利用一种新的频率加权能量算子对含有故障频率的模态分量进行处理，得到其能量谱并提取出轴承故障特征频率，实现轴承故障特征提取和诊断。Li等[19]提出了一种基于频谱特征和MOMEDA方法的轴承故障诊断算法。首先利用Hankel矩阵对原始时域信号进行分割，构造时域分割矩阵，得到信号中各种噪声的表现形式，然后采用频谱融合的方法对信号进行频谱重构，有效地消除了噪声中的随机特性，最后利用MOMEDA构造多点峭度谱，提取边频带内具有周期性冲击特征的故障特征频率。

以上方法对于特定噪声背景下的故障特征增强和识别具有较好的效果，然而这些方法主要是基于滤波的思想，即采用信号滤波器在频域上滤除不相关的噪声而保留有用信息。然而，与电机故障相关的频率成分分布较宽，如果滤波器带宽选择不当，会使信号中有用的信息也被滤除，降低故障诊断的精度。为了克服这一缺陷，本研究提出了一种基于多尺度信号调节的stacked sparse auto-encode (SSAE)方法来提高强噪声条件下电机故障诊断的性能。通过将原始振动信号分解成一系列多尺度特征信号并研究其对故障分类精度的影响，再根据结果加权调整小波系数重构信号，将重构信号提取峭度组成峭度指数序列，最后将一维峭度指标序列转换成二维图片输送到SSAE网络。通过在电机试验台上测试8种电机状态分类结果表明，本文提出的方法相比于传统的SAE方法分类精度提升了5.8%，达到98.1%。同时，本文方法的抗噪声性能也优于传统方法，有望应用于强噪声背景下的永磁电机状态监测和故障诊断。

1 多尺度信号调节自编码器方法

该方法包含两个步骤：第一步将安装在电机上的加速度传感器采集的振动信号采用小波分解得到多尺度特征，将多尺度特征输入SSAE中得到不同尺度对分类精度的贡献率；第二步根据不同尺度信号对分类精度的贡献，对分解的信号进行重构，再次输入SSAE实现电机故障分类。以下分别介绍本文方法所涉及的3个核心算法。

1.1 小波分解

本文首先采集永磁电机的振动信号v[n]，n= 1,2,…,L，L为信号采样点数。采用离散小波变换(discrete wavelet transform, DWT)对v[n]进行分解，如式(1)所示

(1)

1.2 基于SSAE的电机故障分类模型

1.2.1 信号预处理

1.1节将原振动信号分解得到的多尺度特征信号集y[n]，进一步从y[n]中提取特征并进行数据转换成二维矩阵图像，随后利用SSAE对图像进行表征学习，最终实现电机故障模式识别。由于原始振动信号噪声干扰较大，本文从y[n]中提取时域峭度(kurtosis)特征来构造图像。峭度特征对冲击信号敏感，常被用来度量机械振动的剧烈程度，评价振动冲击成分的强弱。同时，考虑到冲击特征隐含在振动信号中，为保留信号相邻元素之间的相关性，同时增加参与深度学习模型训练的样本数量，采用分段重叠截取的方法进行峭度指标的提取，如图1所示。

图1 信号峭度特征提取示意图Fig.1 Illustration of kurtosis feature extraction from the signal

该过程可以表示为，从y[n]信号中截取y[1]～y[p],计算该段信号的峭度，随后移动q个点，截取y[q+1]～y[q+p]并计算峭度。以此类推，实现峭度指标的分段重叠提取，如式(2)所示

(2)

式中：x[τ]为信号的峭度指标序列；T∈Z；p为信号的长度；μ为信号的均值；σ为信号的标准差。在本文中以q= 10个数据为一段计算一个峭度值，并设置重叠率为50%。

将从原振动信号分解得到的多尺度特征信号集y[n]中提取的峭度指标序列进行幅值调节并取整，使其分布在0～255，再将一维的峭度指标序列x[τ]重排为分辨率d×d像素的二维峭度图像，随后输入SSAE网络中进行分类。

1.2.2 SSAE网络

SSAE由多个稀疏自编码器SAE堆叠组成，SAE网络是自编码器AE的一种延伸。AE是一种尽可能使输出x′数据等于输入数据x的无监督学习的神经网络，单层自编码器由编码器(Encode)，激活层(Activation)和解码器(Decode)3个部分组成，其网络结构分为输入层x，隐含层h和输出层x′，隐含层对输入层数据进行编码，输出层对隐含层进行解码重构原始数据，如图2所示。

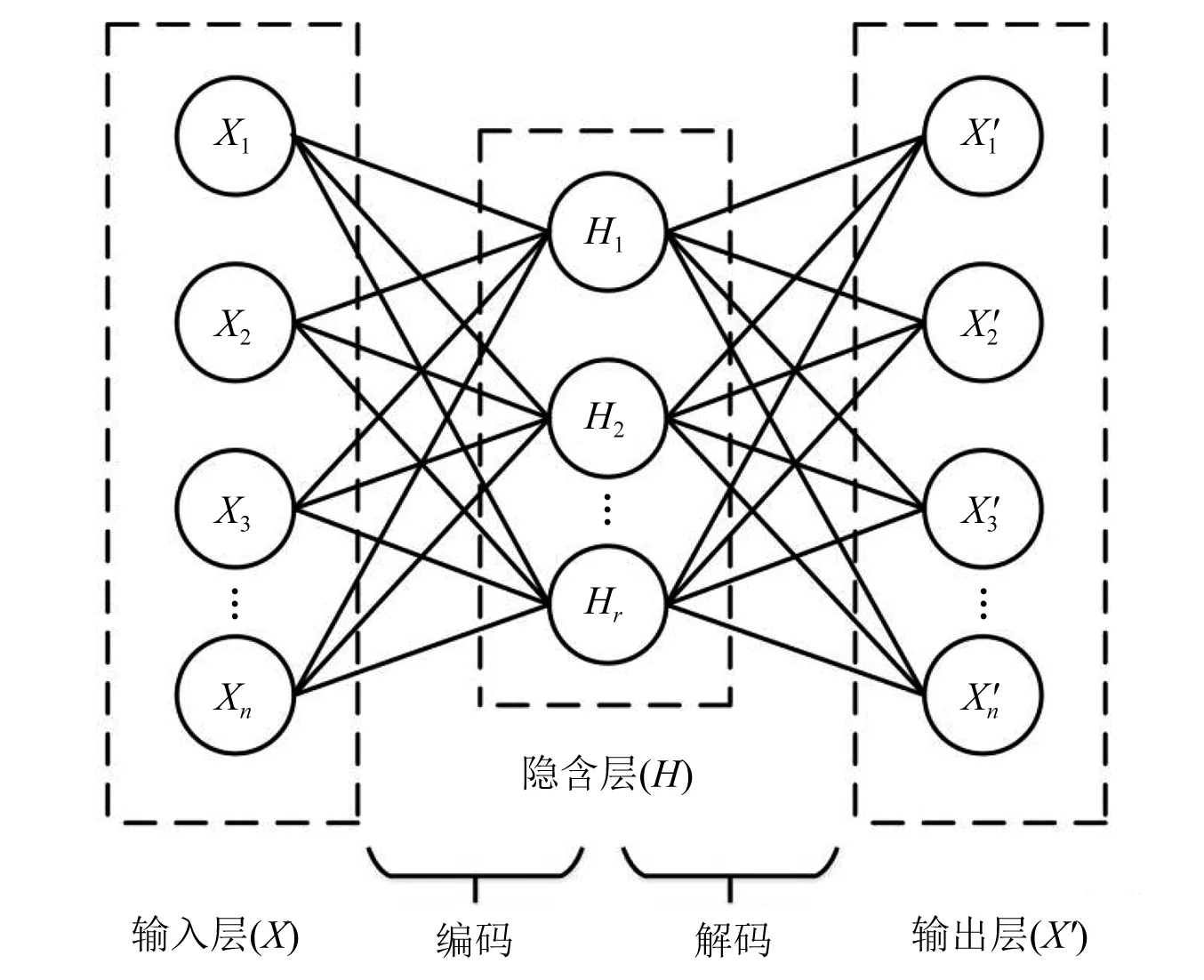
图2 AE结构示意图Fig.2 Schematic diagram of AE

将由一维峭度序列生成的二维峭度图像数据集作为输入数据。输入数据经过编码过程得到隐层表达，编码过程如式(3)所示

(3)

(4)

(5)

输入数据通过反向传播算法由编码层函数和解码层函数进行循环训练，在训练中常通过使Wh=Wx′=W来平衡权重简化网络结构。因此自编码器网络的训练过程可以描述为通过反向传播训练学习参数{W，bh，bx′}来最小化一个损失函数Ω(x,x′)，即最小化输入与重构输出之间的误差。本文中Ω(x,x′)函数被定义为均方误差，如式(6)所示

(6)

式中，y指每个输入样本的特征维数。为了获取更深层次的特征，并减少权重的大小，在损失函数中，常通过添加L2正则化项来防止过拟合，其中正则化项g(W)被定义为

(7)

式中，‖·‖F为Frobenius范数。

当隐藏层神经元数目过多时，通过在添加一种额外的稀疏正则化方式，对隐藏层的输出进行稀疏性约束来实现对数据更深层次的挖掘。其中额外的稀疏惩罚项Φ被定义为

(8)

式中：ši为第i个神经元的平均输出激活量；O为隐含层的神经元个数；š为稀疏参数，SAE通过限制网络的平均激活度ši=š来实现其惩罚方式

(9)

(10)

式中：λ为正则化项权值；β为稀疏正则化项权值。

SSAE是将多个SAE以串联的方式构建起来的深度学习网络。它将上一层的SAE的隐含层作为下一层的输入，通过依次连接来加深网络深度。由于更深层自编码网络比浅层或者线性自编码器能产生更好的压缩效率，因此本文采用拥有更深层的SSAE网络对高维特征数据进行压缩提取。在网络训练中，SSAE采用贪婪训练方法进行逐层训练的，输入的二维峭度图像数据集经过第一层SAE训练得到隐含层特征h1，然后将该特征作为下一层SAE的输入，又通过编码器来获取更深层次的表达。依次重复，从而实现了对高维散射特征更为更深层次的特征进行提取。SSAE网络的结构如图3所示。

图3 SSAE结构示意图Fig.3 Schematic diagram of SSAE

在使用SSAE提取深层次特征之后，采用softmax作为非线性分类器实现电机状态识别。softmax被广泛应用于深度网络的有监督学习分类器中，它与深度网络中的无监督学习相结合，能够很好地提高分类性能。softmax模型如下：对于数据集{(k[1]，k′[1])，(k[2]，k′[2]),…,(k[τ]，k′[τ])}，有k′[τ]∈{1，2，3，…，α}。给定一个测试集样本，样本被判为η类的概率为pi(k′=η|k)，所以对一个α分类问题，输出一个α维的向量

(11)

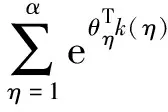
(12)

式中，1{·}为指示函数，大括号内表达式为真则数值为1，反之为0；在实际使用算法时，通常会给上述代价函数增加一个权重衰减项来修改代价函数，则代价函数式变为

(13)

1.3 多尺度信号调节重构

通过将采样频率为fs的原始振动信号v[n]经过N层小波分解得到小波系数集{cAN,cDN,…,cD1}，并重构后得到的一系列多尺度特征信号表示为y[n] = {yAN[n],yDN[n],…,yD1[n]}。将信号集y[n]输入1.2节的SSAE模型进行训练和验证，得到每一个特征信号所贡献的分类精度。假设各个多尺度特征信号所对应的信号带宽和分类精度，如表1所示。

表1 多尺度特征信号的带宽及准确率

通过对表1中不同特征信号的准确率的分析，判断不同带宽信号中所隐含的影响分类精度的信息的强弱。随后，放大精度较高的信号对应的小波系数，同时衰减精度较低的信号对应的小波系数，再次对{cAN,cDN,…,cD1}进行能量调节并重构为

(14)

2 试验平台和数据集

2.1 试验平台

为了验证本文方法的有效性，搭建图4所示的永磁电机试验平台。平台上安装有8个相同型号、不同故障状态的永磁电机。加速度计安装在电机驱动轴侧，信号采集系统采集电机运行时的振动信号，采样频率fs= 10 kHz。8种电机的状态类型包括正常、不同种类的机械故障以及传感器故障，故障类型和标签如表2所示。4种典型故障的说明如图5所示。图5(a)和图5(b)分别为轴承外圈故障和轴承内圈故障，故障采用线切割方式设置而成。图5(c)为霍尔传感器故障，电机采用三相霍尔信号来实现速度闭环控制，通过断开其中一根霍尔线实现霍尔传感器故障设置。霍尔传感器故障会影响电机的正确的换向次序，从而造成电机的异常振动，霍尔传感器故障导致的振动有别于轴承故障等其他故障造成的振动，因而可以通过振动信号分析实现传感器故障检测。图5(d)所示为偏心故障，通过在电机转子上绑定一个不对称的附加质量来设置。由于测试电机自身的尺寸和质量较小，因而本文设定的偏心故障会导致振动异常，其振动特征与其他类型故障不同。

表2 8种电机状态的具体参数

图4 试验平台Fig.4 Experimental setup

图5 4种典型故障类型Fig.5 Four types of typical faults

2.2 数据集

根据1.2.1中的信号预处理方法，以3 925个采样点作为一个信号段，提取信号峭度特征，最终组成一个28 × 28像素的灰度图。每种电机状态选取200个样本进行训练，200个样本进行验证。因此，8种电机状态的训练集和验证集总样本数都为1 600。

3 试验结果

3.1 DWT分解和多尺度特征重构

在本文中，选取Db10小波基对振动信号进行分解和重构，考虑了信号带宽和计算量，将分解层数设置为5层。信号分解后得到的近似和细节系数表示为{cA5，cD5，cD4，cD3，cD2，cD1}。随后根据1.1节的方法构造多尺度特征信号，得到的信号集表示为{yA5[n],yD5[n],yD4[n],yD3[n],yD2[n],yD1[n]}。从数据集中随机选取的一段原始信号及构造的多尺度特征信号，如图6所示。

图6 分解信号和重构的多尺度特征信号Fig.6 Decomposed signal and the reconstructed multiscale feature signals

3.2 多尺度特征信号对分类精度的影响

将图6中的{yA5[n],yD5[n],yD4[n],yD3[n],yD2[n],yD1[n]}信号分别提取峭度并构造图像，输入SSAE网络中实现图像的分类。SSAE网络参数如表3所示。

表3 SSAE参数

3.3 多尺度特征信号调节与重构

不同多尺度特征信号在相同的SSAE模型下的分类精度，如表4所示。根据表4中多尺度特征信号对分类准确率的影响，再结合多次试验的结果分析，确定增强分类精度最高的yD2和yD1分量对应的小波系数cD2和cD1，其他分量能量保持不变，即通过小波系数{cA5,cD5,cD4,cD3,16×cD2,16×cD1}重构信号。其中加权因子16参考了文献[20]中的多尺度噪声调节方法。

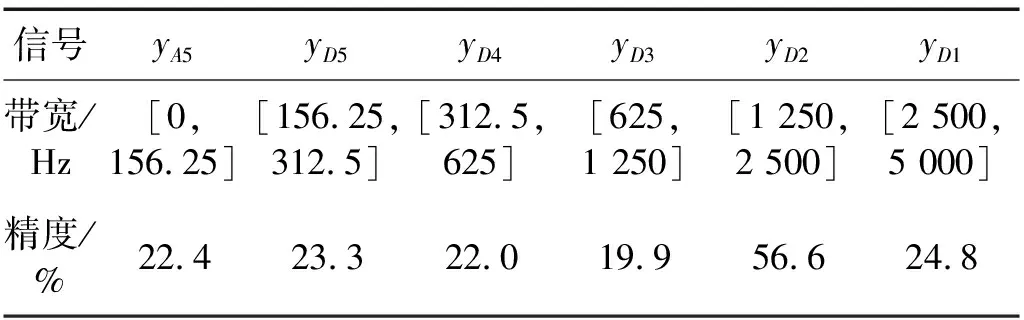
表4 多尺度特征信号的带宽及分类准确率

3.4 本文方法对电机故障状态的识别效果

按照以上方法对表2中的8种电机信号进行重新处理，最终得到转化的图像如图7所示。将这些图像输入SSAE进行训练，再通过softmax层进行故障诊断和分类，得到分类混淆矩阵如图8所示。从图8中可见，在总共1 600个测试样本中，只有30个样本没有被正确分类，分类的准确率为98.1%。为了方便对比，同时将原始振动信号经过处理输入SSAE网络中进行识别，得到的分类准确率只有92.3%。对比结果表明，本文提出的方法提升了5.8%的分类精度。

图7 8种电机信号生成的图片Fig.7 The generated images of 8 types of motor signals

图8 本文提出方法对电机状态进行分类的混淆矩阵Fig.8 The confusion matrix for motor fault classification using the proposed method

3.5 抗噪声干扰能力测试结果

考虑到在电机在实际工作过程中会受到多种噪声干扰，为了验证本文方法的鲁棒性，向采集到的原始振动信号中添加不同强度噪声来模拟实际中的噪声干扰。添加噪声的标准差强度D分别为0.2,0.4,0.6，将添加噪声后未经处理的含噪信号和经过本文方法处理的信号输入SSAE网络进行分类，对比结果如图9所示。可见，随着噪声强度的增加，本文方法和传统方法的分类精度都在下降，但是本文方法仍比传统方法下降的趋势较慢，本文方法比传统方法精度平均高8.1%，说明本文方法在强噪声情况下具有较好的抗噪性能。

图9 不同噪声强度下的分类准确率Fig.9 Classification accuracies under different noise intensities

3.6 对比研究

为了进一步验证本文方法的优势，本小节将本文方法与当前常用于故障诊断的深度学习方法进行对比。其中每种故障的训练样本和验证样本数分别为200和50，总的训练和验证样本数分别为1 600和400。对比方法1采用基于卷积神经网络的模型，该方法首先将振动信号通过傅里叶变换得到信号频谱，再将频谱转化为二维图像输入卷积神经网络进行识别[21]。对比方法2采用堆叠去噪自编码器，首先采用采用无监督学习方法对网络模型进行预训练，再采用有监督学习方法对网络进行优化微调[22]。对比方法3为基于长短时记忆网络模型，该方法直接利用时域振动信号对轴承的运行状态进行诊断[23]。

不同方法处理相同数量的样本信号的结果,如表5所示。可见，基于卷积神经网络的方法识别精度较高，达到96.8%，基于堆叠去噪自编码器和长短时记忆网络的识别精度略低，分别为92.3%和88.7%。综合比较，本文提出的方法精度最高，达到98.1%。因此，在振动信号受到噪声干扰较大时，本文提出的多尺度特征调节的方法能够更好地提取微弱信号特征，从而获得更高的故障诊断精度。

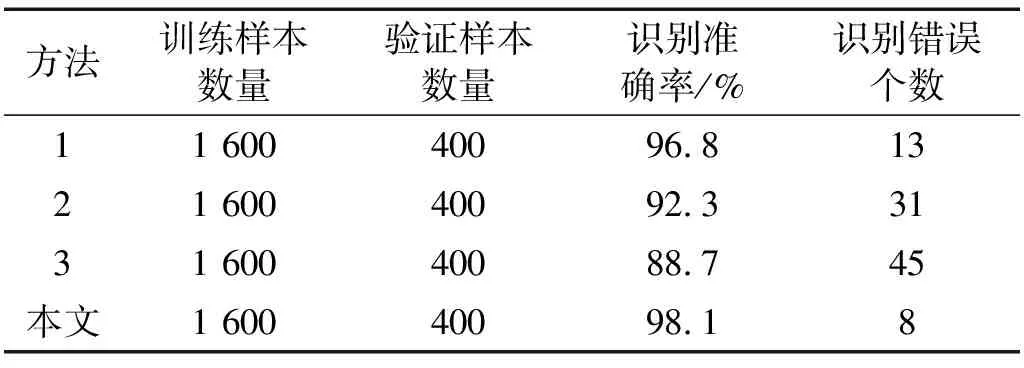
表5 不同方法的对比试验结果

4 结 论

本文提出一种多尺度信号调节自编码器方法用于永磁电机振动信号特征提取及故障诊断。通过将原始振动信号分解成一系列多尺度特征信号并研究其对故障分类精度的影响，再根据结果加权调整小波系数重构信号。将重构信号输入SSAE模型中，能够有效增强电机故障的分类精度。提出方法的有效性和鲁棒性在永磁电机平台上得到验证，试验结果表明该方法相比于传统方法，精度得到了有效提升并且具有更好的抗噪声性能。本文方法有应用于强背景噪声下的永磁电机状态监测和故障诊断。