一种基于TC-CAE的轴承寿命预测方法

2022-08-05李海浪刘永志邹益胜刘彦涛宋小欣

振动与冲击 2022年14期

李海浪，刘永志，邹益胜，刘彦涛，宋小欣

(西南交通大学机械工程学院，成都 610031)

由于制造业的快速发展，旋转机械的应用场景变得越来越复杂，轴承作为大型旋转机械的关键零部件，对整个机械系统的可靠运行起着至关重要的作用[1]。根据相关统计分析的结果，约30%的旋转机械故障是由滚动轴承的异常运行引起的。预测和健康管理(prognostics and health management， PHM)是近年来一项新型的技术，剩余使用寿命预测是PHM中的重要部分。精准地预测轴承剩余使用寿命能及时发现运行故障，排除安全隐患，及时更换轴承更能提高设备使用过程中的经济性[2]。剩余寿命预测方法主要可以分为两大类：一是基于模型的预测方法；二是基于数据驱动的预测方法。基于模型的预测方法是根据失效机理来建立数学或者物理模型，但是在现实中，由于系统的复杂性和随机性，理解所有的故障模型和退化过程无疑是困难的，这限制了基于模型方法的适用性。基于数据驱动的预测方法是根据传感器采集的数据，利用机器学习和概率统计等方法，建立样本数据和剩余使用寿命之间的映射关系。基于数据驱动方法的优势是可以在没有太多先验知识的情况下，从输入数据中提取特征，同时进行剩余寿命预测。近年来随着深度学习和工业大数据的快速发展，基于数据驱动的预测方法已经逐渐成为主流[3]。

基于数据驱动的预测方法主要分为三步：数据采集、特征提取和剩余寿命预测。尽管基于数据驱动的预测方法已经取得了不错的成果，但还是面对众多挑战，首要问题便是如何有效提取特征[4]。特征的好坏直接影响后续模型的预测精度。目前在特征提取工作上，学者们提出了许多模型和方法，例如卷积神经网络[5-6]、深度信念网络[7]、自编码等。其中，自编码作为一种无监督学习方法，目的是在保证重要特征不丢失的情况下，降低输入信息的维度，在自动提取特征上十分有效，目前在轴承剩余使用寿命预测上取得了众多进展。陈仁祥等[8]提出了一种加噪样本扩展深度稀疏自编码，完成寿命特征的自动提取与表达，同时抑制了网络过拟合并提升网络鲁棒性。李华新等[9]用分层稀疏自编码提取特征，更加准确地识别数据内部信息，提高了预测精度。张继冬等[10]提出一种基于全卷积变分自编码网络的轴承剩余寿命预测方法，增强了特征提取过程中的抗干扰能力，从而提升整体网络的预测稳定性。王久健等提出了一种无需先验知识的基于空间卷积长短时记忆神经网络，可直接从采集到的原始信号中挖掘反映退化程度的特征。Kaji等[11]利用卷积自编码构造了一个轴承健康指标。试验结果表明，该指标表现出单调递增的退化趋势，并在轴承的早期退化阶段具有良好的性能。

以上方法所提取的性能退化特征虽然可以从某个方面反映性能退化过程，但是他们都尚未考虑退化特征的轴承个体差异性，即忽略了同一特征的变化趋势在不同轴承上是具有差异的。轴承由于制造工艺以及运行环境的不同，不同轴承的退化过程是不一致的。即便是工艺参数和工况相同，轴承运行时由于受到诸多复杂因素的影响，其状态有着不确定性、非线性和时变性，退化过程也很难相同。退化过程的不同便会导致退化特征具有个体差异性，最终造成预测模型的预测效果不佳。已经有相当多的学者已经提出在进行可靠度预测的同时也要考虑轴承的个体差异，减少轴承特征的个体差异性有利于增强预测方法的适用性，以及提升预测精度[12-14]。刘弹等[15]提出在评价退化特征时，需要明确退化特征的变化趋势是否具有一致性，趋势一致性越好的特征更能反映轴承的性能退化过程。Zhao等[16]提出使不同轴承的寿命周期性能退化特征曲线呈现一致性趋势，可以提升剩余寿命预测模型的准确性。提升特征的趋势一致性，实际上也是降低了退化特征在时间方向上的轴承个体差异性，是有利于预测的。

综上所述，为了解决在提取特征时对退化特征的轴承个体差异性考虑不足的问题，本文通过构造特征趋势一致性约束，再结合卷积自编码强大的特征提取能力，最终提出了趋势一致性约束卷积编码(trend consistency convolutional auto-encoder, TC-CAE)特征提取模型。该模型在自动提取特征的同时，有利于促进同一特征在不同轴承上的趋势一致性，从而提升预测精度。具体预测流程为，先利用快速傅里叶变换将时域信息转化为频域信息，再用TC-CAE模型提取特征，最后用长短期记忆网络(long short-term memory, LSTM)进行预测。

1 基本理论

1.1 卷积自编码

自编码是深度学习中的一种无监督算法，主要目标是对输入数据进行表征学习，常应用于特征提取。自编码包含编码器和解码器两部分，其中编码器由输入层和中间隐藏层组成，解码器由中间隐藏层和输出层组成。编码层的输入节点和解码层输出节点个数相等，目的是通过学习一个恒等函数，使输出等于输入，以此实现隐藏层特征提取。

卷积神经网络具有局部感知和参数共享两个特点：局部感知即卷积神经网络的节点仅仅和其前一层的部分节点相连接，只用来学习局部特征，然后在更高层将这些局部的信息进行合并，从而得到全部表征信息；参数共享网络结构类似于生物神经网络，降低了网络模型的复杂度，减少了权值的数量，同时能解决自编码网络因为层数增加，参数呈指数增长的问题。传统的自编码器一般使用全连接层，结合自编码和卷积神经网络的优点，用卷积池化层代替编码器和解码器中的全连接层，由此诞生了卷积自编码(convolutional autoencoder，CAE)。卷积自编码结构如图1所示。

图1 卷积自编码结构Fig.1 Convolutional autoencoding structure

在输出维度和输入维度相同的情况下，损失函数L(·)，例如均方误差(mean-square error，MSE)可以用于在训练阶段更新网络权重。

(1)

1.2 数据预处理

利用快速傅里叶变换将原始振动数据从时域信号转换为频域信号。每个训练轴承数据按照采集的先后顺序各自整理成(m×n)的数组，其中：m为采集总次数；n为对应时间点的数据量。轴承的寿命标签采用百分比标签yi，标签值在1～0，yi计算表达式如式(2)所示。这实则上也是对寿命标签进行归一化处理，便于神经网络在优化时使用梯度下降算法进行求解，同时弱化了轴承在不同工况、不同寿命数值之间的差异，有利于提高剩余使用寿命的预测精度。在预测应用时可根据已服役的寿命值与对应的标签还原出实际剩余寿命值。

(2)

式中：j为该行对应的行数；m为总行数。

卷积自编码的数据输入，常规方式是将一个训练轴承的数据按照批量(batch size)依次输入，完毕后轮换下一个训练轴承。提取特征时，为了对同一特征在不同轴承间的趋势一致性进行计算，然后通过约束增强特征的趋势一致性，需要将所有轴承的数据并行输入。具体方式是将每个轴承训练集按照各自数据采集次数的总数mi分为x等份，即x个[int(mi/x)×n]数组，int(·)表示取整函数。此处关于x可以根据实际的情况取相应的值，本文以x=50为例来说明训练集数据的构建方式。由于各训练轴承的采集次数mi不同，因此不同轴承每等份样本数目[int(mi/x)]是不一致的，但是对应的寿命标签区间长度都为0.02。将各轴承相同寿命标签区间的数据按照顺序进行拼接，组成每次卷积自编码网络的输入训练数据，其样本总数目为网络的bitchsize，表达式如式(3)所示。具体操作如图2所示。

(3)

式中：h为训练轴承的总个数；mi为各轴承所对应的采集次数；x为均分数目；int(·)为取整函数。

图2 训练集构建方式Fig.2 Training set construction method

1.3 趋势一致性约束

将处理好的数据输入到CAE中，得到每个轴承的隐藏特征。通过对每维特征在不同轴承上的趋势一致性不断进行局部约束，从而实现全局约束。设隐藏特征中某轴承的一个特征序列为X1=(α1,α2,α3,…,αk)，在另一个轴承上对应同一特征序列为X2=(β1,β1,β1,…,βk)。借助相关性计算公式计算同一特征在不同轴承之间的趋势一致性，相关性计算公式如式(4)所示，其中K表示序列的长度。

Corr(X1,X2)=

(4)

利用相关性公式计算时，需保证两个序列具有相同的长度。但是由于轴承寿命具有离散性的特点，这导致了不同轴承同一特征之间的序列长度有很大差异，无法运用相关性公式对不经处理的特征进行计算。在不改变特征整体变化规律的前提下，将不同轴承的同一特征压缩至相同长度。如图3所示，特征A具有长度a1和数值范围b。通过等区间取平均值的降采样方法，在不改变特征整体趋势的前提下，将特征A长度从a1压缩至a2。具体示意图如图3所示，m和q分别表示降采样前后的样本数量，本文q取5。

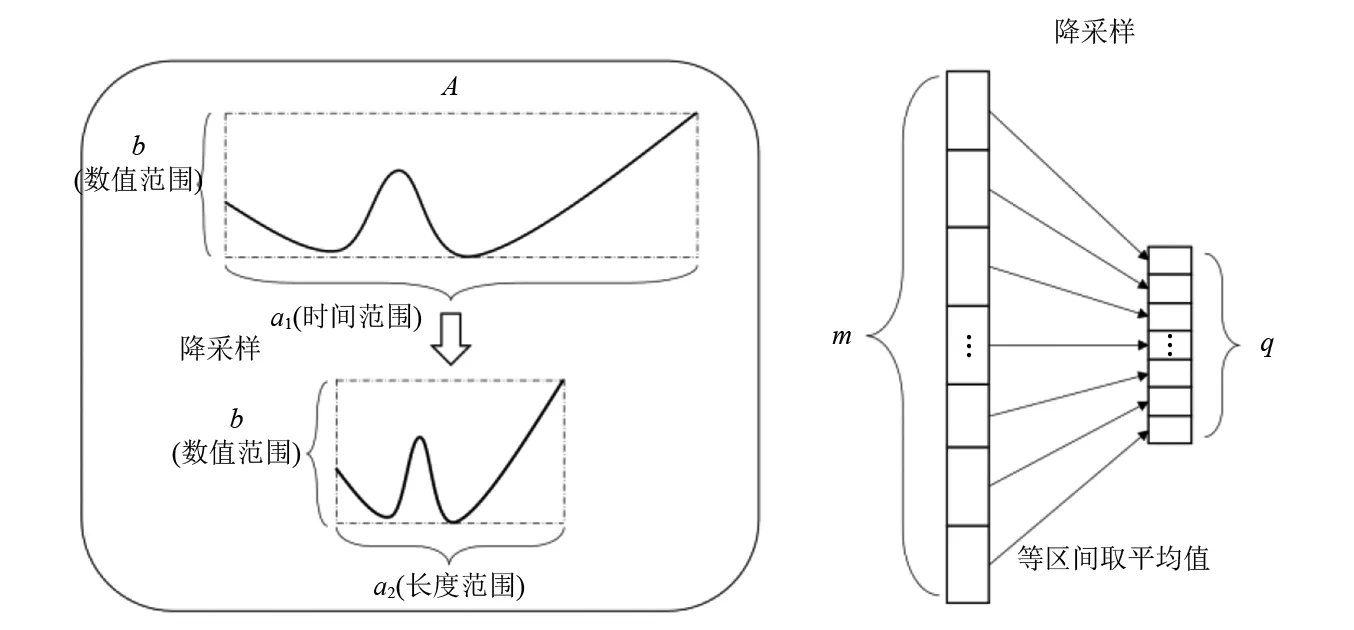
图3 降采样Fig.3 Down sampling

(5)

对式(6)计算出的上三角矩阵取平均值，平均值作为该列特征的趋势一致性大小Cr。Cr计算方式如式(6)。所有特征的趋势一致性大小TC也是取平均值，计算方式如式(7)。

(6)

(7)

式中，h为降维后特征的维数。

1.4 TC-CAE模型

自编码提取训练轴承特征时，自编码的主要损失函数是原始数据与重构数据的误差，从而使得所提取的特征尽可能地保留原有数据的大部分信息。在卷积自编码的重构损失中加入趋势一致性约束，在提取特征时，通过最小化带有趋势一致性约束项的损失函数来增强同一特征在不同轴承上的趋势一致性。设趋势一致性约束为TC，TC值越大表明特征趋势一致性越好，而卷积自编码的重构损失越小，表明隐藏特征越能表征原数据。在趋势一致性约束前增添一个负号来保持整体损失函数的减小，那么TC-CAE模型的损失函数可以表达为式(8)。TC-CAE模型原理如图4所示。

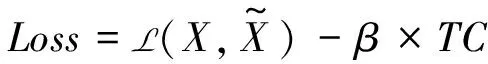
(8)

图4 TC-CAE模型原理图Fig.4 Schematic diagram of TC-CAE model

2 预测流程

2.1 特征提取

轴承振动信号往往是多维数据而且含有噪声，预测模型会面临特征维数灾难和提取特征不佳的问题。在频域信号中，频带是按照频率大小进行排列，比原始振动信号的分布更为规律，且这种按频率大小顺序排列的特点使得输入层的单个网络单元的输入数据是固定频率的信号，不再像原始振动信号一样属于振动周期中随机时间的信号，可以有效降低卷积自编码网络重构信号的难度，所以更适合作为卷积自编码网络的输入。因此对原始轴承振动时域信号作快速傅里叶变换，转化为频域信号，随后用TC-CAE网络提取特征。深度学习模型有更强的特征学习能力，能够更充分地学习到很多浅层网络学习不到的特征，因此TC-CAE网络设置了三层卷积层与三层反卷积层，其结构如图5所示。

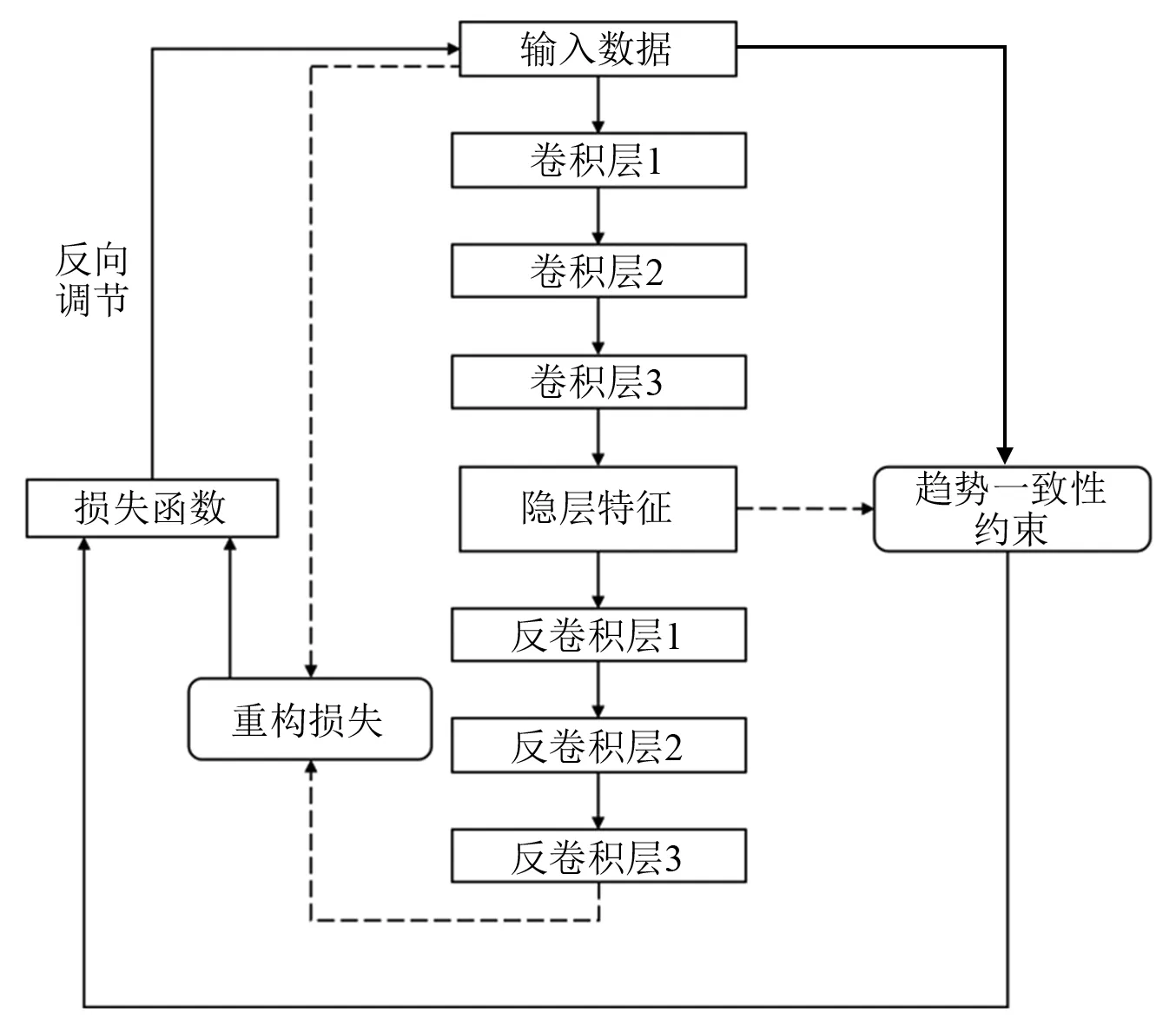
图5 TC-CAE模型Fig.5 TC-CAE model

2.2 预测模型

在轴承性能退化的过程中，振动信号的变化与时间有关，轴承振动数据间的时序信息是一种潜在的信息。深度学习中的LSTM可以处理较长的时间序列数据，能够利用这种时序信息提高轴承寿命的预测精度，因此采用多层的LSTM网络作为预测模型[17]。LSTM结构如图6所示。全连接层将输出结果映射到1～0。由于预测RUL结果之间的独立性，预测结果的连续性较差。实际情况表明，轴承的RUL往往是连续的，因此对预测的RUL结果进行平滑可以使预测结果更符合实际情况。整个模型包含三层LSTM网络层和一层全连接，同时对输出的预测结果进行加权平滑。

图6 LSTM结构Fig.6 LSTM structure

综上，预测总流程为：首先利用快速傅里叶变换，将轴承原始振动时域信息转化为频域信息；再用TC-CAE网络提取特征；最后构建LSTM模型进行轴承寿命预测。总路线如图7所示。

图7 总流程Fig.7 Overall process

3 试验验证

3.1 试验数据

试验数据为滚动轴承加速寿命台架试验采集的振动加速度数据，来源于电气和电子工程师协会2012年举办的PHM数据挑战赛[18]。试验数据来自于PRONOSTIA试验平台，该试验台能够对轴承在数个小时的时间内完成性能退化试验。数据集共包含3种工况下的17个滚动轴承的全生命周期振动数据，数量分别为7、7和3，分别命名为Bearing1-1～Bearing1-7，Bearing2-1～Bearing2-7和Bearing3-1～Bearing3-3。数据采样频率为25.6 kHz，每间隔10 s采集一次，采集时间长度为0.1 s，一次采集的振动数据为2 560个振动加速度，直到满足数据说明中的振动加速度达到设定阈值轴承失效条件就停止采集。

图8 PRONOSTIA试验平台Fig.8 PRONOSTIA test platform

本文在该轴承数据集中每种工况下随机选择了几个轴承进行试验，并选取工况1中的Bearing1-3和工况2中的Bearing2-4作为测试轴承，具体如表1所示。将每个轴承的试验数据按照采集先后顺序分别整理成数组。其中，Bearing1-3一共采集了2 375次，每次采集2 560个振动加速度，其寿命为23 750 s，经过快速傅里叶变换后将其整理为(2 375×1 280)的数组。所对应的剩余寿命标签为1～0的等差数列，以第200条数据为例，其对应的寿命标签为0.916。同理Bearing2-4经过快速傅里叶变换后整理成(751×1 280)的数组。

表1 试验轴承数据Tab.1 Experimental bearing data

3.2 模型参数

将每个训练轴承的频域数据纵向均分为50份，剩余寿命标签区间为0.02，然后TC-CAE网络的batchsize，其中Bearing1-3和Bearing2-4的batchsize分别为302和344。根据输入数据的长度尺寸，特征提取模型的参数设置如表2所示。将数组(batchsize×1 280)的频域特征压缩为数组(batchsize×160)的隐层特征，计算趋势一致性时将隐层特征降采样为10个(5×160)的数组。

模型训练时，训练步数为10 000，并使用衰减学习率保证前期训练速度的同时防止后期难以收敛。模型训练完成之后，使用平整层将卷积层3的输出数据扁平化为一维的数据，其长度为160。将训练集和测试集分别输入训练完成的网络模型，分别获得训练集特征与测试集特征。

表2 模型参数Tab.2 Model parameters

三层LSTM隐藏神经元数目分别设置为：170，40，10，步长选择为5。全连接层的神经元数量为1，激活函数采用relu函数。模型训练时，采用的优化器为Adam，训练步数为10 000，初始学习率为0.005，并且采用衰减学习率的方式，学习率衰减因子设置为0.95。最后采用加权平均的方法对预测结果进行平滑处理。

3.3 趋势一致性分析

在试验过程中，为了验证TC-CAE网络在增强特征趋势一致性上的有效性，与不加趋势一致性约束的普通卷积自编码网络进行对比，网络采用相同的参数。模型训练完毕以后，分别用TC-CAE和CAE模型获得Bearing1-3和Bearing2-4的特征，并计算得到对应的160维特征的趋势一致性值。由于文章篇幅有限，只展示了Bearing1-3作为测试集时部分特征的趋势，每个工况选择了一个训练轴承。采用图片的方式展示训练集中Bearing1-1、Bearing2-7和Bearing3-1中第61维特征，如图9～图14所示。

图9 CAE Bearing1-1第61维特征Fig.9 CAE Bearing1-1 61st dimension features

图10 CAE Bearing2-7第61维特征Fig.10 CAE Bearing2-7 61st dimension features

图11 CAE Bearing3-1第61维特征Fig.11 CAE Bearing3-1 61st dimension features

图12 TC-CAE Bearing1-1第61维特征Fig.12 TC-CAE Bearing1-1 61st dimension feature

图13 TC-CAE Bearing2-7第61维特征Fig.13 TC-CAE Bearing2-7 61st dimension features

图14 TC-CAE Bearing3-1第61维特征Fig.14 TC-CAE Bearing3-1 61st dimension feature

从图9～图14分析中可以发现，图12～图14的特征趋势一致性是优于图9～图11的，说明TC-CAE模型相比于CAE模型，所提取的第61维特征趋势一致性更好，验证了TC-CAE特征提取模型确实是有利于促进同一特征在不同轴承上的趋势一致性。表3展示了TC-CAE模型第61维特征在所有训练轴承上的相关性系数，计算结果精确到小数点后三位。

表3 第61维特征的相关性值Tab.3 Correlation value of the 61st dimension feature

为了更加定量地说明TC-CAE模型的有效性，计算了第61维特征对应的趋势一致性数值，其中TC-CAE上该维特征的Cr值为0.857，CAE上该维特征的Cr值仅为0.423。Bearing1-3作为测试集时，所有特征的趋势一致性TC值在CAE上为0.466，在TC-CAE为0.684。TC值越大表明特征的趋势一致性越好，说明TC-CAE模型的确增强了所提特征的趋势一致性。

3.4 试验结果

本文模型主要由TC-CAE特征提取网络与LSTM预测网络组成，为了验证TC-CAE特征提取网络的有效性，将该网络与卷积自编码特征提取网络进行对比，预测模型均采用相同参数的LSTM网络。同时，进一步与当前主流的轴承剩余寿命预测方法进行了对比，即特征评价[19]和CNN[20]。

以Bearing1-3和Bearing2-4依次作为测试轴承进行试验，采用上述4种方法分别对测试轴承进行剩余寿命预测。Bearing1-3和Bearing2-4的预测结果分别如图15和图16所示。图中横坐标表示数据序号，实则代表的是使用时间，纵坐标为当前时间点对应的剩余寿命占总寿命的百分比，黑色实线为真实的寿命值，其他线条为各种方法预测的寿命值。

图15 Bearing1-3预测结果Fig.15 Forecast results of Bearing1-3

从图15和图16可以看出，无论是在Bearing1-3还是Bearing2-4中，本文所提方法相比CAE-LSTM预测效果是有提升的，更加接近真实的寿命线。此现象可以说明在提取特征时，增强同一特征在不同轴承上的趋势一致性确实是有利于提升预测精度，TC-CAE是可行的。同时对比其余两种参考方法，也是优于它们的，能够取得更好的预测结果。为了更加精确地描述以上4种方法的预测结果，按照式(9)对两种方法预测结果的平均误差emean进行了计算，计算结果如表4所示。

(9)

图16 Bearing2-4预测结果Fig.16 Forecast results of Bearing2-4

表4 各方法预测结果平均误差Tab.4 Average error of prediction results of each method

通过计算：对于Bearing1-3，本文方法相比CAE-LSTM预测模型的平均误差下降了47.7%，相比特征评价和CNN分别下降了71.1%和75.1%；对于Bearing2-4，分别下降了62.4%，83.2%和66.7%。上述结果表明本文所提方法比CAE-LSTM、特征评价和CNN模型的预测误差更小，有利于提升轴承剩余寿命的预测精度。

3.5 留一法试验

为了更全面地验证该方法的有效性和适用性，采用留一法进行预测试验。留一法即每次只采用一个轴承作为测试集，其余轴承作为训练集，模型训练完毕后，利用测试集进行测试。4种模型的平均误差emean如表5所示。

表5 留一法试验结果Tab.5 Leave one experiment results

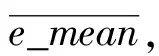
表6 综合平均误差Tab.6 Combined average error

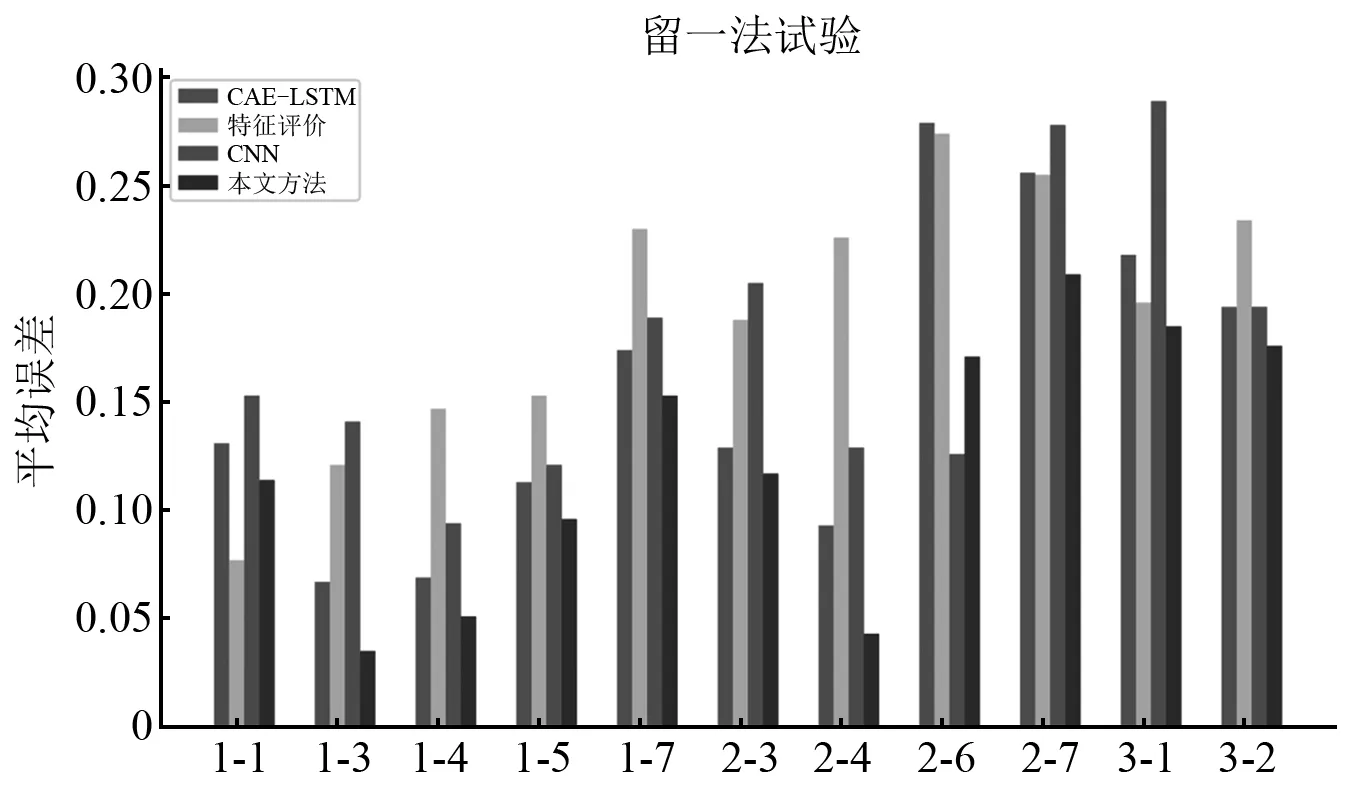
图17 留一法试验Fig.17 Leave one experiment

分析表6中的数据，本文方法TC-CAE的综合平均误差也是以上几种方法中最小的，相比于CAE-LSTM的预测结果，综合平均误差降低了21.1%，相比于特征评价和CNN分别降低了35.6%和25.9%。进一步分析以上结果，TC-CAE用深度卷积自编码来提取特征，结合了卷积神经网络的表征学习能力与深度自编码的强大重构能力，因此相比于CNN会有更好的预测效果。而相比于CAE，由于TC-CAE在提取特征时加入了趋势一致性约束，促进同一特征在不同轴承上的趋势一致性，降低了退化特征的轴承个体差异性，因此在CAE的基础上提升了预测精度。