四旋翼飞行仿真器的姿态控制

高伟翔

北京信息科技大学自动化学院高动态导航技术北京市重点实验室，北京 100192

0 前言

近年来，人们对控制方法的研究从经典控制发展到智能控制以及多种控制融合，在控制系统里的应用也从线性到非线性，从简单到复杂[1]。针对多变量控制系统对扰动敏感等问题，经典控制略显局限，因其仅适用于单输入单输出的线性定常控制系统，而采取现代控制和智能控制应用于复杂系统是现今控制领域的需求和方向[2-4]。当前研究中，对于旋翼机系统在真实作业中携带重物（如药瓶等物资）而产生质量变化影响稳定性的问题有待解决，同时也需要综合考虑旋翼机负重工作时可能遇到复杂干扰（如在狭小地带拍照、田间作业及运送物资时易受障碍物、植物或小动物的碰撞干扰）并对之敏感的问题[5-6]，因此，所设计的控制器的性能有待优化[7-8]。

四旋翼飞行仿真器是一套多变量控制系统，用于模拟旋翼机在空中工作的姿态控制[9]。本文在该实验平台上添加配重以模拟四旋翼机携带重物，建立LQR和粒子群优化LQR姿态控制系统，分别做多组多种类的实时控制实验，在实验结果中取超调、响应时间以及稳态误差做比较，从控制性能、鲁棒性以及抗扰性3方面分析两种控制系统的性能。

1 四旋翼飞行仿真器的建模和分析

1.1 系统的建模

四旋翼飞行仿真器实验平台的工作机制是由4个螺旋桨电机带动扇叶转动，由产生的反作用力提供动力，使得螺旋桨上升、下降或风力对螺旋左右摆动，使得仿真器实验平台在笛卡尔坐标系下进行3种姿态运动（俯仰、滚转和偏航），如图1所示。其中，Ff、Fl、Fr、Fb分别为某一时刻螺旋桨电机转动所产生的风力。

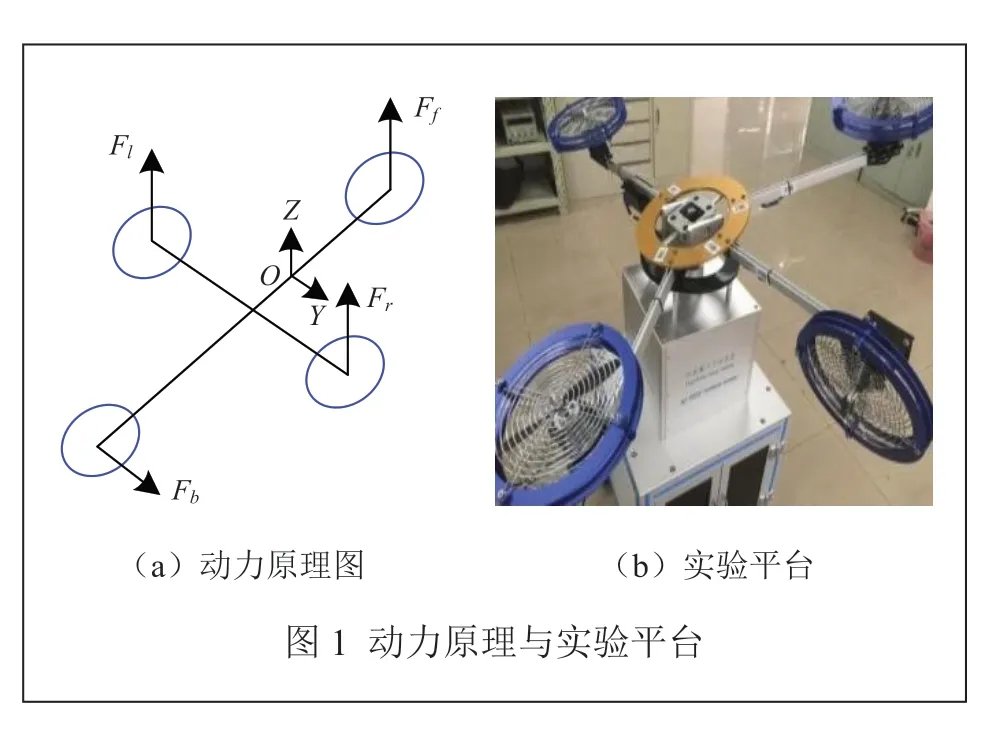
通过实验装置的具体结构进行姿态动力学分析。

建立基于笛卡尔坐标系的3个角度姿态量的平衡态力矩模型：

（1）假设在静态平衡的情况下，系统的重心位于偏航轴，忽略摩擦以及旋翼自身阻尼的力矩；

（2）忽略旋翼到达所需转速需要的时间；

（3）设定逆时针转为正方向，合外力矩方程（M=J*α）和力矩平衡公式（M=F*L）；

（4）定义绕OY轴向上运动的方向为俯仰角P正方向，机体处于水平状态时的俯仰角度为0，此时只分析其在OY轴的转动，则滚转角为0。做俯仰轴的受力分析，如图2所示。

推导得俯仰角的力矩平衡方程，如式（1）所示：其中，JP——俯仰轴转动惯量；

Ff——前向螺旋桨扇叶转动产生风力的反作用力；

Lf——前向螺旋桨转动产生风力的反作用力的力臂；

Fl——左向螺旋桨扇叶转动产生风力的反作用力；

Lc——左、右向螺旋桨转动产生风力的反作用力的力臂；

Fr——右向螺旋桨扇叶转动产生风力的反作用力。

做滚转轴受力分析，如图3所示。

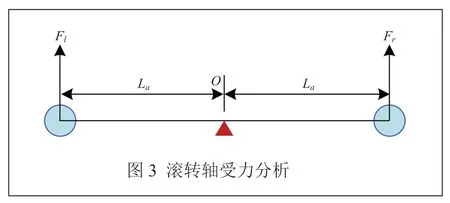
推导得滚转角的力矩平衡方程，如公式（2）所示：

其中，JR——滚转轴转动惯量；

La——左、右向螺旋桨转动产生风力的反作用力的力臂。同理，推得偏航角的力矩平衡方程，如公式（3）所示：

其中，JY——偏航轴转动惯量；

Fb——后向螺旋桨扇叶转动产生风力的反作用力；

Lb——后向螺旋桨转动产生风力的反作用力的力臂。

在公式（1）～（3）里，对一些参量做计算，如公式（4）～（6）所示：

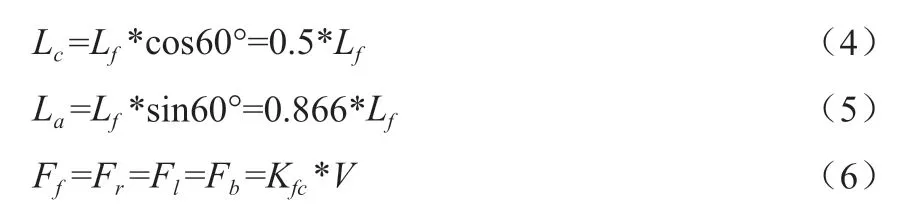
其中，V——电机电压；

Kfc——偏电压/升力（牛顿/伏特），经过检测，值为15.0 N/V。

Lf为0.5 m，JP、JR、JY计算后的值分别为0.9112 kg*m2、0.4050 kg*m2、1.3066 kg*m2。

将参数代入，可得仪器的近似数学模型，如式（7）～（9）所示：

其中，Vf——前向电机的电压；

Vr——右向电机的电压；

Vl——左向电机的电压。

其中，Vb——后向电机的电压。

将系统分为偏航、俯仰及滚转3个通道去考虑。

2 控制系统的分析与设计

实际中，控制器需快速对各种变化作出反应，减小对工作状态的影响，使系统快速回至稳定。

2.1 线性二次型最优控制系统设计

2.1.1 理论分析

LQR控制有2个特点：其状态方程是线性的；系统的泛函数是由状态变量和输入变量组成的二次类型。该控制方法的最优解可以经过解析形式表达成状态变量的线性函数[10]。

假设线性系统的空间状态描述方程为：

其中，x(t)——系统的状态变量；

y(t)——系统的输出变量；

u(t)——系统的输入变量；

A——系统状态变量矩阵的系数矩阵；

B——系统输入变量矩阵的系数矩阵。

由原理，需寻找状态反馈律：u=-k*x，使指标J最小化，如公式（11）所示：

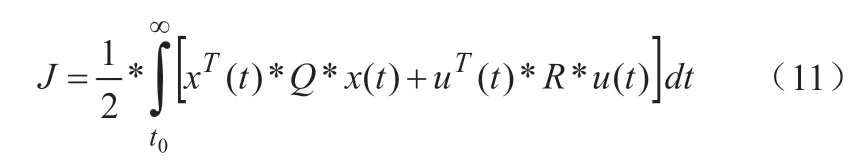
其中，J——LQR控制算法里的指标函数；

Q——指标函数J中对应状态量的矩阵；

R——指标函数J中对应控制量的矩阵。

Q是正定或半正定对称矩阵，R是正定对称矩阵。Q阵所反映的是对状态过渡过程性能的要求，R阵所反映的是对控制能量的限制。构建出Hamilton函数，如公式（12）所示：

在输入u(t)不受约束下，求H最小值，求导并令其值为0，如公式（13）所示：

λ可由式（15）求出：

其中，P——中间变量。

2.1.2 系统搭建

LQR最优控制可由状态反馈实现闭环最优，适用于时变系统，稳态误差小，鲁棒性较好，且对于线性、定常、具备强耦合的多变量控制系统具有好的控制效果。选用9状态量的LQR的控制方法设计控制模块，将控制变量与状态变量结合成的二次型积分函数当作指标函数，最后确立最佳控制输入，使性能指标取极小值，以设计得到恰到好处的最优的控制器。

由LQR最优控制方法求出全状态反馈增益量K，具备较好的鲁棒性。

对于LQR最优控制而言，要选取合适的两个加权矩阵Q和R。Q矩阵为diag(q11q22q33q44q55q66q77q88q99)，由其各主对角元素影响控制器的整体性能，在调试时，要根据实际需求在输入和输出之间寻找一个平衡处，从而实现最优控制。

适当选择加权矩阵Q与R，做到在控制信号与输出性能间实现恰到好处的平衡。多次实验后，发现取

R=diag(1 1 1 1)，Q=diag(10 0.01 0.1 10 0.01 0.5 0.1 1 1)的效果最好。

结合MATLAB的函数lqr2()，求得符合系统性能要求的K阵。

结合LQR方法的理论和上述公式，可以由MATLAB求出K，如公式（18）所示：

四旋翼飞行仿真器仪器平台结合MATLAB/Simulink进行实时控制，结合实时工具箱搭建控制系统进行控制任务的实现。在Simulink中搭建的9状态的LQR控制系统如图4所示。

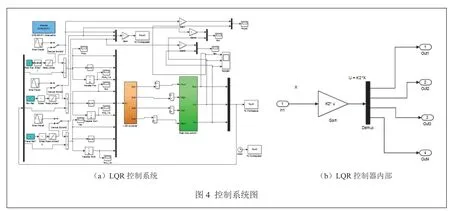
图4中的Real time control模块是实时控制子模块，负责采集编码器数据以及输出控制信号。LQR controller是控制器，控制器的内部子模块所示的4个支路分别连接实时控制模块的4个电机，即先把求出的K值分别带入4个子模块，之后整个控制器将前面的9个状态量转换成4个电压量传递给电机，同时也控制实验仪器的4个电机带动所连接螺旋桨进行合适的转动，产生风力，控制3个姿态轴的姿态。

2.2 粒子群算法优化LQR控制系统设计

2.2.1 控制理论分析

群智能算法中的粒子群算法是通过无质量的粒子模拟鸟群。每个粒子都有速度（移动的快慢）与位置（移动的方向）。

该算法的优点是实现简单且无需大量调参，在控制系统科研领域有广泛应用[11]。涉及迭代更新，先初始化一群随机粒子（即随机解），通过迭代找到最优解。在每次迭代中，粒子要参考两个极值（个体最优位置pbest(i)，全局最好位置gbest）去更新本身的两个属性。

粒子群算法的流程如下：

（1）初始化一个粒子群，包含群体规模、每个粒子单独的位置xi和速度vi；

（2）计算得出每个粒子的适应值F(i)；

（3）分别将每个粒子当前的适应值F(i)和其个体极值（即其经历的最优位置）pbest(i)的适应值F(pbest(i))作比较，如果前者小于后者，则用前者代替后者（即更新个体极值），除此之外，后者仍取当前值作为个体极值，作为粒子i当前的最优位置；

（4）分别将每个粒子更新后的个体极值的适应值和全局极值（即整个群体的最优位置适应数值）gbest的适应值F(gbest)进行比较，较小的位置更新为全局最优位；

（5）结合式（19）与（20）：

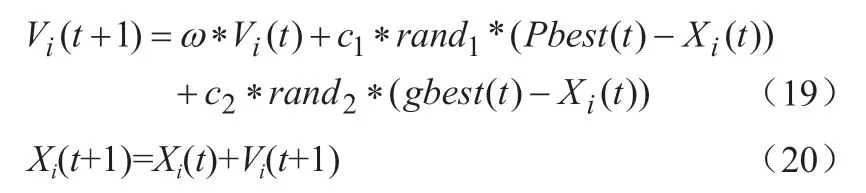
其中，rand1、rand2——[0,1]上的随机数；

c1、c2——学习因子；

t——迭代的次数，和rand1、rand2一起更新粒子速度和位置；

Pbest(t)——当前迭代次数下的个体最优极值；

gbest(t)——当前迭代次数下的全局极值；

Xi(t)——当前迭代次数下的粒子i的位置；

Xi(t+1)——下次迭代后粒子i的位置；

Vi(t)——当前迭代次数下的粒子i的速度；

Vi(t+1)——下次迭代后粒子i的速度。

ω是非负惯性权重因子，取值大，则全局性寻优强，局部寻优弱；取值小，则全局寻优弱，局部寻优强；ω的取值由线性递减权值取ω，即式（21）：

其中，Gk——最大迭代次数；

ωini——初始的惯性权值；

ωend——迭代到最大的代数的惯性权值。

典型的取值ωini为0.8，ωend为0.5，引入ω，性能有显著完善。

2.2.2 系统搭建

LQR控制的核心是使目标函数值最小，根本在于Q和R矩阵的主对角线取值，用粒子群优化更具科学性，去调节Q和R矩阵的科学性强[12]，能求出使目标函数最小化的Q和R矩阵的主对角线值。

结合模型，搭建LQR控制器。经粒子群优化LQR控制离线仿真，设定30个粒子，迭代100次。因仪器启动所需时间，则优化得出的最优解经多次调整，结果如图5～7所示，分别为Q矩阵的主对角线的9个数值，R矩阵的主对角线的4个数值以及粒子群优化LQR算法的目标函数变化曲线。

当迭代到100次时，MATLAB得出13个最优解（即Q和R矩阵的总共13个主对角线元素值），用粒子群最优解的形式表达为：x(1)=63.430092，

x(2)=0.100000，x(3)=0.001000，x(4)=41.352183，x(5)=0.100000，x(6)=0.001000，x(7)=10.000000，x(8)=0.100000，x(9)=0.000100，x(10)=0.100000，x(11)=0.100000，x(12)=0.100000，x(13)=2.16771。目标函数值减小至1.8637。由图7可知，在粒子群不断更新Q和R矩阵时，目标函数值变小，证明粒子群优化LQR科学有效。由LQR求K矩阵，如式（22）：

将K矩阵带入LQR控制器，进行后续实验。

3 半实物仿真实验

3.1 仪器

3.1.1 仪器选用

现实中的旋翼系统非线性、多变量、强耦合，为研究姿态控制，选用四旋翼飞行仿真器作研究对象进行半实物仿真实验。

3.1.2 配重添加

旋翼机在现实作业中往往需要携带药品（如田间撒药）、相机（航拍）等任务所需物品。

为满足其复杂应用性而不损害仪器且初状态平衡，将3瓶瓶装水分别挂在旋翼机的左、前、右3个翅膀上。设所挂配重质量分别为M前、M左、M右，M左=M右，且左右两旋翼的所挂配重同力臂，则横向实现力矩平衡不再做分析，只需分析纵向。据测算，左右旋翼和后向轴的夹角均为60°，则左右两旋翼作用到后向轴的力臂L后均为左（或右）旋翼力臂L左（或）L右×cos60°。设前向轴的力臂为L前，则：L前×M前×g=L左×M左×g+L右×M右×g，令所挂瓶装水均为500 g，力臂均为34 cm。

3.2 实验

通过MATLAB的Simulink，结合仪器，根据LQR控制、粒子群优化LQR进行半实物仿真实验。记录实验结果，以俯仰姿态为例，对比分析两控制系统的性能。

3.2.1 控制性能检测

分别对两系统做阶跃响应实验。要合理检测控制性能，则设置系统的给定姿态角[3, 3.5, 10]，观察平台从初状态到给定姿态的阶跃响应。两组控制系统姿态曲线对比如图8所示。

对系统分别采取LQR控制与粒子群优化LQR控制时，俯仰及滚转两个方向中，两系统的超调控制在1°以内，调节时间均小于2 s，稳态精度高，在0.7°以内。偏航方向，LQR控制系统的超调量不超过4°，调节时间为3 s左右，稳态精度很高；粒子群优化LQR控制系统的超调量不超过0.8°，调节时间在3 s左右，稳态精度高。

3.2.2 鲁棒性检测

为验证设计的控制系统的鲁棒性，使配重水的质量可变。将瓶装水和旋翼仿真器视为一个整体，既可以模拟鲁棒性检验中内在因素，即实验仪器的质量变化，又可以模拟实际作业中旋翼机所带工作重物发生变化的工作状态（如旋翼机在田地间播撒农药时，农药的质量在不断减小）。

给定姿态角[3, 3.5, 0.4]，3瓶水的质量同时从500 g开始，以相同的速度逐渐流出，分别对两系统做实验，记录结果，两系统的姿态曲线对比如图9所示。

俯仰及滚转两方向中，两系统的超调均非常小，调节时间较短，稳态精度高，在1.5°以内。偏航方向中，LQR控制系统的超调不超过2°，调节时间一般，稳态精度高；粒子群优化LQR控制系统的超调不超过1°，调节时间一般，震荡小，稳态精度高。

3.2.3 抗扰性检测

实际飞控中，会受外界不可控因素干扰。既然无法从源头遏止干扰，那就在外界因素产生的干扰来临后，令系统迅速做出反应，飞行器快速变回稳定且最大程度接近于受扰前的状态。

3.2.3.1 抗常规干扰性能检测

常规干扰指有一定规律和相干性的干扰，这类干扰可恒定不变，也可规律性变化。

在Simulink里，对两种系统的电控模块的4个电极上分别加干扰。VF前加全程正弦波干扰，幅值：5，频率：0.5*2*pi；VR前加全程白噪声干扰，能量：[0.2]，sample：0.1；VL和VB前加全程阶跃信号干扰，Step time：20。设给定姿态[3, 3.5,40]，记录结果，两系统的姿态曲线对比如图10所示。

俯仰及滚转两方向中，两系统震荡小，稳态精度高，不超过2°。偏航方向中，LQR控制系统超调不超8°，调节时间不超过5 s，震荡小，稳态精度高；粒子群优化LQR控制系统超调不超过5°，调节时间不超过4 s，震荡小，稳态精度高。

3.2.3.2 抗突变类干扰性能检测

突变干扰是指变化无规律性的干扰类型。为了能够全面且科学地研究系统的抗扰性能，做抗软件信号类突变扰动实验和抗外部碰撞类突变扰动实验。

3.2.3.2.1 抗软件信号类突变抗扰性能

在Simulink里对两系统的4个电极分别加干扰：VF、VR、VL、VB均加随机噪声，最小值和最大值分别是-5和5，Sample time：0.1。设给定姿态角[-0.9,1.4, 10]，两系统的姿态曲线对比如图11所示。

俯仰及滚转两方向中，两系统稳态精度高，不超过2°。偏航方向中，LQR控制的超调不超过3°，调节时间不超过4 s，震荡小，稳态精度高；粒子群优化LQR控制的超调不超过2°，调节时间不超过4 s，震荡小，稳态精度高。

3.2.3.2.2 抗外部碰撞类突变抗扰性能

旋翼机在实际中会遇到不可控的突变式碰撞干扰，如旋翼机在田间飞行播洒农药时被高粱秆或者鸟碰撞干扰，或在危险环境中拍摄受到树枝碰撞干扰等。

在仪器运行的实验过程中，用手向实验仪器的旋翼臂施加推力。设给定姿态[-1, 1.4, 10]，观察实验平台从初始状态到给定姿态的阶跃响应。两系统分别在14 s时施加推力（使3个姿态角均变化）。两系统的姿态曲线对比如图12所示。

3个姿态方向：两系统受干扰后，在1.3 s内恢复受扰前的工作状态，稳态精度高，保持在1°以内，震荡小。

4 结果分析

由本实验的四旋翼飞行仿真器的建模仿真和3种实验验证，可做出如下分析：

（1）由动态响应实验可知，本文设计的LQR控制器和粒子群优化LQR控制器可以达到要求，系统超调量小，调节时间短，响应速度快，稳定性高，证明控制器有效；

（2）相较于同类研究成果，本文对于实验仪器进行合理改造，通过水量逐渐减少的实验，既可以实现鲁棒性检验的要求，又能模拟旋翼机在飞行中携带重物量不断减少的工作情况，具备实验的科学及全面性。由该鲁棒性实验可知，设计的两种控制系统具备良好的鲁棒性，且本文通过粒子群优化LQR控制算法，使得LQR参数调优效率更高、更准确。通过实验丰富地研究了抗扰性；

（3）相较于同类研究成果，本文借助特定实验仪器平台，引入了较复杂的常规性干扰实验和突变式干扰实验，后者还分为软件信号类干扰和外部碰撞类干扰，对于抗扰性的分析更具备全面性和科学性。由抗扰实验可知，本文设计的两种控制系统对于常规干扰和突变干扰均可有效抵抗，其中，粒子群优化LQR控制的抗扰效果较优。两种控制系统在受到干扰后，均能快速调整旋翼姿态使其恢复期望的平衡态；

（4）本文设计的两种控制器的参数调试很重要，无论是LQR控制的加权矩阵参数调节，还是粒子群算法进行公式参数调整再结合粒子数和迭代次数调节，最终影响Q和R矩阵，合适的参数可以提高系统的响应速度和精度。粒子群优化LQR算法适应性强，比人工试凑参数的方法效率高，科学性强，而且控制效果不弱于同类研究成果中使用粒子群优化PID控制的性能。

5 结束语

本文先由动力学分析对四旋翼飞行仿真器控制系统进行建模，设计出合理选择加权矩阵的LQR控制器和粒子群优化LQR控制器，用MATLAB/Simulink建立四旋翼飞行仿真器系统。之后从控制性能、鲁棒性以及抗扰性3个角度结合半实物实时控制仿真去检测控制系统的多方面性能，实验结果表明，本文设计的控制系统响应快，到达稳态值所需时间短，超调量小，在所携带的重物质量逐渐减小的情况下，控制系统响应结果较为稳定地保持在期望值附近，鲁棒性强；在遇到内外部多种复杂的常规和突变式干扰时，系统反应迅速，能较快地恢复到受扰前的工作状态并保持较好的稳定，抵抗干扰能力强。

综上所述，本文设计出的合理选择加权矩阵的LQR控制器和粒子群优化LQR控制器，作为最优控制以及与智能控制的有效结合，对像四旋翼飞行仿真器这样的多变量控制系统具有较好的控制性、鲁棒性和抗扰性。以上两套控制方法的有效运用也能为其他类似的工程控制系统提供理论和参考价值。