完全分配可交换子空间格代数上的非线性广义Lie导子*

马飞，张建华，刘红哲

1. 咸阳师范学院数学与信息科学学院，陕西 咸阳 712000

2. 陕西师范大学数学与信息科学学院，陕西 西安 710062

设A 是任意代数，M 是其A-双模。一个可加映射d：A →M 称为导子，Jordan 导子或Lie 导子，如果d满足对任意A，B∈A，有d(AB) =d(A)B+Ad(B)，d(A2)=d(A)A+Ad(A)或者d([A，B]) =[d(A)，B]+[A，d(B)]成立。设d是一个Lie 导子，若存在一个可加导子ϕ和交换子上为零的映射ξ使得d=ϕ+ξ，则称Lie 导子d具有标准型。特别地，若无可加假设，即对任意A，B∈A，d都满足d([A，B]) =[d(A)，B]+[A，d(B)]，则称d是非线性Lie 导子。

1991 年，Brešar 在文献［1］中引入了广义导子的概念。设f：A →M 是一个可加映射，如果存在导子d：A →M 使得对任意A，B∈A 有f(AB) =f(A)B+Ad(B)，那么称f是广义导子；若满足f(A2)=f(A)A+Ad(A)，则称f是广义Jordan 导子。Hvala[]2于1998 年引入了广义Lie 导子。设f：A →M 是一可加映射，如果存在一可加映射d：A →M，使得对任意A，B∈A有

那么称f是广义Lie 导子。显然，（广义）导子一定是（广义）Jordan 导子，（广义）导子一定是（广义）Lie 导子，反之一般不成立（如文献［3-4］）。关于Lie 导子或者广义Lie 导子的一个自然研究课题就是在那些代数上的（广义）Lie 导子具有标准型。如文献［5-9］分别得到了环或者某些代数上的Lie 导子具有标准型，文献［10-12］研究了上三角矩阵代数、三角代数和von Neumann 代数上的非线性Lie 导子，文献［13-14］分别研究了三角代数上的广义Lie 导子和非线性广义Lie 导子。

设H 是实数域或复数域F 上的可分Hilbert 空间，L 是H 上的子空间格，A lg L ={T∈B(H)：T(L) ⊆L，∀L∈L}，是L上的子空间格代数。若L中任意投影是可交换的，则称L是交换子空间格，简称CSL，一个全序子空间格N称为套；相应地，A lg L 和AlgN称为CSL 代数和套代数。称CSL 是完全分配格，如果对0 ≠e∈L 都有e=V{L∈L：N-⊇L}，其中N-=V{P∈L：P⊇N}. 完全分配的CSL代数称为完全分配可交换子空间格代数，简称CDC-代数。关于完全分配格的标准定义及相关研究内容见文献［15-16］。

由文献［17］可知，CDC-代数是由其包含的秩一算子弱*闭生成的算子代数，这个结果对研究CDC-代数具有重要的意义。在CDC-代数A lg L 中，记U(L) ={e∈L：e≠0，e-≠H}，称U(L)中的e，e′是连通的，如果存在e1，e2，…，en∈U(L)使得ei与ei+1可比，e0=e，en+1=e′(i= 0，1，…，n). 设C ⊆U(L)，称C 是U(L)的一个连通分支，如果C 中任意两个元素是连通的，并且C 中的任何元素与U(L)C 中的元素都不连通。设L是复可分的Hilbert 空间H上的一个完全分配的交换子空间格，由文献［18］可知，A lg L是不可约的当且仅当其交换子是平凡的，即其一次换位是FI，也等价于L ∩L⊥={0，I}，其中L⊥={e⊥：e∈L}. 显然，套是完全分配的交换子空间格，也是最重要的模型。Gilfeather 等［18］证明了任何一个CDC-代数都可以分解成可数个不可约CDC-代数的直和，这个结果在研究CDC-代数的同构和导子等问题时具有非常重要的作用，下面我们给出这个结论。

引理1[18]设A lg L 是复Hilbert 空间H 上的CDC-代数，那么存在ε(L)的可数个连通分支Cn：n∈Λ，使得ε(L) = ∪{e：e∈Cn，n∈Λ}. 令en=V{e：e∈Cn，n∈Λ}，则{en，n∈Λ}⊆L ∩L⊥两两正交，并且

其中每个(A lg L)en是Hilbert 空间en上的不可约CDC-代数，这里的收敛指的是强收敛。

下面这个引理对研究不可约CDC-代数具有非常重要的意义。其证明了不可约CDC-代数上的Jordan 同构是一个同构和反同构之和。这个结论在文献［19］中已经给出了证明。

引理2[19]设A lg L 是Hilbert 空间H 上的不可约CDC-代数，则存在一个非平凡投影e∈L，使得e(A lg L)e⊥是忠实的A lg L-双边模。这里忠实的A lg L-双边模指的是对于任意的A∈A lg L，若Ae(A lg L)e⊥={0}，则有Ae= 0；若e(A lg L)e⊥A={0}，则有e⊥A= 0.

记H 中的恒等算子为I。若L 是非平凡的，即A lg L 是非自伴算子代数，则由引理2 知，存在非平凡投影e∈L，使得e(A lg L)e⊥是忠实的A lg L-双边模。令e1=e，e2=I-e，则e1，e2均为A lg L 中的投影。因而对于任意的不可约CDC-代数A lg L 中的A，均可分解为A=e1Ae1+e1Ae2+e2Ae2. 记Aij=ei(A lg L)ej，因而可将A lg L代数分解为

受上述结论的启发，本文主要研究了完全分配可交换子空间格代数上的非线性广义Lie 导子。

1 不可约CDC-代数上的非线性广义Lie 导子

在本节中，我们先讨论不可约CDC-代数AlgL上的非线性广义Lie 导子。其主要结论如下。

定理1 设A lg L 是复Hilbert 空间H 上的不可约CDC-代数，f：A lg L →A lg L 是A lg L 上的非线性广义Lie 导子，d是A lg L 上与f相关的非线性映射。则存在可加导子ψ，ϕ：A lg L →A lg L，使得对于任意的A∈A lg L，有

其中ξ是A lg L到其中心且在交换子上为零的映射。

下面通过几个引理来完成定理1 的证明。

引理3 设f是满足定理1的非线性广义Lie导子，则对任意Aij∈Aij(i，j= 1，2) 有

证明

（i）由式（1）易得f(0) = 0，且当B=I时，有

令A= 0即得d(0) =f(0) = 0.

对任意Aij∈Aij，由f(0) = 0和Aii Ajj= 0(i≠j)知

上式两边同乘以e1得e1f(A22)e1A11=A11e1d(A22)e1⊆A11，从而

注意到A11，A22的中心为Fe1，Fe2，因此存在λA22∈F，使得

类似存在λA11∈F，使得e2f(A11)e2=e2d(A11)e2=λA11e2.

（ii）在式（3）中左乘e1右乘e2，可得

令A11=e1，A22=e2可得e1f(e1)e2= -e1d(e2)e2. 上式中分别取A11=e1和A22=e2，有

由引理3可知，对任意A11∈A11，定义ξ1：A11→Fe2，则存在λA11∈F，使得

类似地，定义ξ2：A22→Fe1，则存在λA22∈F，使得

显然有，ξ1([A11，A11]) =ξ2([A22，A22]) = 0.

引理4 设f是满足定理1 的非线性广义Lie 导子，则f(A12)，d(A12) ⊆A12.

证明 对任意A12∈A12，由[e1，A12]=A12=[A12，e2]得

和

式（4）和式（5）两边分别乘以e1和e2，有

从而f(A12)，d(A12) ⊆A12.

对任意A∈AlgL，令

容易验证，F依旧是关于D的非线性广义Lie 导子，满足对任意A，B∈AlgL，

引理5

（i）F(A11) ⊆A11，F(A22) ⊆A12+ A22；

（ii）D(A11) ⊆A11+ A12，D(A22) ⊆A22.

证明 对任意Aii∈Aii，由引理3 可知

类似地可以证明D(A11) ⊆A11+ A12，D(A22) ⊆A22.

引理6 对任意A，B∈A lg L，

证明 对任意A，B∈A lg L，由F(A) -D(A) =F(I)A-AD(I)可得

因此，F(A+B) -F(A) -F(B) =D(A+B) -D(A) -D(B).

记θ(A，B) =F(A+B) -F(A) -F(B) =D(A+B) -D(A) -D(B)，则有下面的结论。引理7 对任意Aij∈Aij，有

证明 在式（6）中，取A=A11，B=A12，由引理4和引理5 可得

引理8 对任意Aij∈Aij，有θ(A11，A12)，θ(A12，A22) ∈FI.

证明 对任意Aij，Bij∈Aij，由引理4 和 引理7 知

因此，对任意B12∈A12，有θ(A11，A12)B12=B12θ(A11，A12)，结合引理4和引理5 可知

对任意A12∈A12，由引理5 知

比较等式两端得，A12D(e2)= 0. 由A12的任意性及引理6 知D(e2)= 0. 特别地

由F(A12)，D(A12) ⊂A12，知F(A12)=e1F(A11+A12)e2. 代入式（7）得θ(A11，A12) ∈FI.

类似可证θ(A12，A22) ∈FI.

引理9 对任意A12，B12∈A12，有θ(A12，B12)= 0.

证明 在引理8中分别取A11=e1和A22=e2，则存在λ1，λ2∈F，使得θ(e1，A12)=λ1I，θ(B12，e2)=λ2I.注意到A11+B12=[e1+A12，B12+e2]，从而由引理3和引理4 及D(e2)= 0得

由引理6 得θ(A12，B12)= 0.

在引理6中用B+C替换B易得

记为θ(A，B，C). 则有下面的结论。

引理10 对任意A=A11+A12+A22∈A lg L，Aij∈Aij，有θ(A11，A12，A22) ∈FI.

证明 对任意Aij，Bij∈Aij，由于[A11+A12+A22，B12]=A11B12-B12A22∈A12，利用引理5和引理6 得

利用引理7，引理9又可得到

因此对任意B12∈A12，有

利用引理4和引理5 可得

类似于引理8的证明，可得F(A12)=e1F(A11+A12+A22)e2-e1F(A22)e2. 进而有θ(A11，A12，A22) ∈FI.

由引理10，对任意A=A11+A12+A22∈A lg L，记

引理11F，D是可加的广义Lie 导子。

证明 在引理10 中，令A11=e1，A12= 0，A22=e2，由D(e2)= 0知，存在λI∈F使得

则对任意Aij∈Aij，由式（2）知

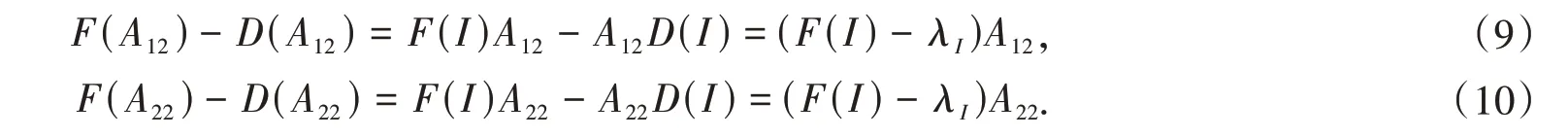
因此，将式（9）和式（10）分别代入引理7 得

对任意Aij，Bij∈Aij，由式（11）得

又由θ(A11A12，B11A12)= 0知

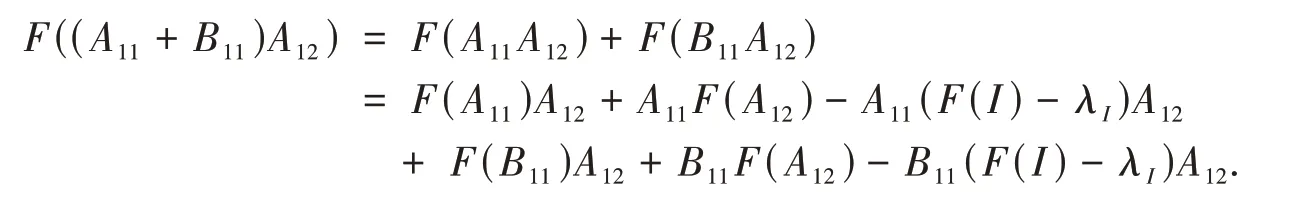
从而对任意A12∈A12，有θ(A11，B11)A12= 0. 即θ(A11，B11)= 0.

类似可以证明θ(A22，B22)= 0.

对 任 意A=A11+A12+A22，B=B11+B12+B22∈A lg L， 注 意 到θ(A，B) =θ(A11+B11，A12+B12，A22+B22) ∈FI，从而存在λA，λB，λA+B∈F使得

从而F-θ0是可加的。注意到F(A+B) -θ0(A+B) =F(A) +F(B)，由上式可得θ0也是可加的，进而F是可加的广义Lie 导子。

由引理6 知，D也是可加的广义Lie 导子。

引理12 对任意Aii，Bii∈A lg L，有

（i）F(A11B11)=F(A11)B11+A11F(B11)-A11(F(I) -λI)B11，

（ii）F(A22B22)=F(A22)B22+A22F(B22)-A22(F(I) -λI)B22.

证明 对任意Aij，Bij∈Aij，由式（11）知，

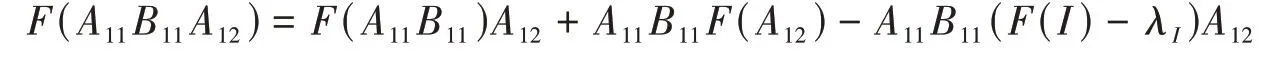
和

成立。比较上两式可知，对任意A12∈A12，有

从而由引理2 知

类似地可以证明F(A22B22)=F(A22)B22+A22F(B22)-A22(F(I) -λI)B22.

定理1 的证明

对任意A=A11+A12+A22，B=B11+B12+B22∈A lg L，由式（10）知，

从而由引理4和引理5，引理11和引理12 及上式可得

由λI=θ0(I)知，F-θ0是可加的广义导子。由式（3），引理6 及θ0的定义可知

因此，D-θ0也是可加的广义导子。

下面说明θ0([A lg L，A lg L]) = 0. 由F(A11) ⊂A11知

特别地，在式（6）中取A=A11，B=B11∈A11，利用引理5可得

因此，对任意A，B∈A lg L，易得

类似地，e2θ0([A，B])e2= 0，从而有θ0([A lg L，A lg L]) = 0.对任意A∈A lg L，由F，D以及θ0的定义可得，

和

令ψ(A) =(F(A) -θ0(A)) +[A，e1f(e1)e2]，ϕ(A) =(D(A) -θ0(A)) -[A，e1d(e2)e2]，ξ(A) =ξ1(A) +ξ2(A)+θ0(A).

由前面证明可知，ψ，ϕ均是不可约的CDC-代数A lg L 上可加的广义导子，ξ是不可约的CDC-代数AlgL到其中心FI且在交换子上为零的映射，且有

2 CDC-代数上的非线性广义Lie 导子

下面研究任意CDC-代数上的非线性广义Lie 导子。本文的主要结论如下

定理2 设A lg L 是复Hilbert 空间H 上的完全分配可交换子空间格代数，f是A lg L 上的非线性广义Lie 导子，d是A lg L 上与f相关的非线性映射。则存在可加导子ψ，ϕ：A lg L →A lg L 使得对任意A∈A lg L有

其中ξ是A lg L到其中心且在交换子上为零的映射。

证明 设en=V{e：e∈Cn，n∈Λ}为引理1 中的投影，由引理1 知，任意的完全分配可交换子空间格代数A lg L均可分解为不可约的情形，即A lg L =∑n∈Λ⊕(A lg L)en，则对任意en有

由于en=V{e：e∈Cn，n∈Λ}是Hilbert 空间H 中的投影，自然也是Hilbert 空间。因此，(A lg L)en是一作用在Hilbert 空间en上的不可约CDC-代数，并且这里的收敛是强收敛。因而由en的定义可知，其线性张是整个Hilbert 空间H，并且两两正交，AlgL 的单位元为I=∑n∈Λ⊕en，中心元为Z(A lg L) =∑n∈Λ⊕λnen，其中λn∈F.

对任意A∈A lg L和投影en，(A lg L)en均是Hilbert 空间en上的不可约CDC-代数。设f，d满足式（1），且fn，dn分别为f，d在Alg(enL)上的限制，即在Alg(enL)上有f=fn，d=dn. 由定理1 可知，存在可加导子ψn，ϕn：Alg(enL) →Alg(enL)和在交换子上为零的映射ξn：Alg(enL) →Fen使得对任意A∈Alg(enL)，

在引理3 中，对于每一个广义导子ψn均存在一个导子，设为τn，使得对于任意的A，B∈Alg(enL)有，ψn(AB) =ψn(A)B+Aτn(B). 又由文献［17］，CDC-代数是由其包含的秩一算子弱*闭生成的算子代数，则任取E∈U(L)，x∈E，固定y∈，有x⊗y∈Alg(enL)且是一秩算子。任取一秩算子u⊗v∈Alg(enL)，则对任意A∈Alg(enL)，有

设{Ak}，A∈Alg(enL)，并且{Ak}强收敛到A，由上式可知，当k→∞时

(u⊗v)τn(Ak)(x⊗y) =ψn((u⊗v)Ak(x⊗y)) -ψn(u⊗v)Ak(x⊗y) -(u⊗v)Akτn(x⊗y)收敛到

由一秩算子u⊗v∈Alg(enL)的任意性得，τn是强收敛的，进而ψn也强收敛。

下面证明在任意CDC-代数A lg L 上结论也成立。设{Ak}，{Bk}，A，B∈A lg L，并且{Ak}，{Bk}强收敛到A，B. 因为A lg L =∑n∈Λ⊕(A lg L)en，并且en是两两正交的投影，所以对每个投影ei，{Akei}，{Bkei}强收敛到Aei，Bei并且

则对于Hilbert 空间H中的任意元x，注意到ψn，ξn的定义，并结合定理1的证明可知，当k→∞时

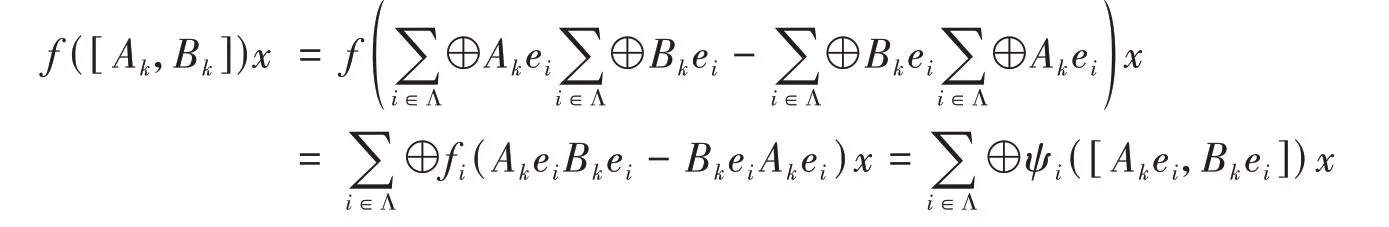
收敛到

即f是强收敛的，进而d也强收敛。因而对任意A∈AlgL 都有f(A) =(Aen). 因为fn(Aen)=ψn(Aen)+ξn(Aen)，dn(Aen)=ϕn(Aen)+ξn(Aen)，则对任意A∈AlgL有

和

证毕