含高架桥的实际街区交通颗粒物扩散模拟*

陈同，罗银萍，陈进财，刘永红

1. 中山大学智能工程学院，广东 广州 510006

2. 广东省交通环境智能监测与治理工程技术研究中心，广东 广州 510275

3. 广东省环境科学研究院，广东 广州 510045

4. 广东工业大学土木与交通工程学院，广东 广州 510006

城市化进程的快速发展，使得街道纵横交错，交通干道两侧建筑向高层高密度化发展，城市街区大气环境不断恶化，如风速降低、空气污染加重等［1-2］，其中细颗粒物（PM2.5）污染尤为严重，受到高度关注。研究表明：城市颗粒物主要来源于机动车尾气的一次排放及二次转化［3］，易导致交通热点区域形成高浓度污染分布。城市街区居民与行人长期或短期暴露于颗粒物高浓度环境，易引起心肌梗塞、肺炎等一系列疾病［4-5］。因此，研究城市街区内交通颗粒物扩散特征，对改善人居环境具有重要意义。

城市大气污染问题是多尺度的大气流动问题，按空间尺度可划分为道路尺度、街区尺度和城市尺度。大量文献针对单条峡谷型道路流场及污染物扩散进行了研究，主要揭示街道高宽比［6］、绿化带［7］、地面加热［8］等对污染物扩散的影响机理。目前很多大中型城市选择建立高架桥来缓解日益严重的城市交通拥堵压力，高架桥不仅带来了新的交通排放源，还破坏了街谷内流场的稳定性，进一步增加了街区交通尾气污染问题的复杂性。近年来，部分学者研究了含高架桥道路的二维理想街谷模型，考虑了高架桥结构、声屏障、地面及高架桥污染源等参数的影响［9-12］。与理想街谷型道路相比，城市街区由结构复杂多变的道路、建筑物、树木等以不同密度、排放方式组成，各道路交通流及气象参数具有时变性，导致城市街区内污染物扩散的时空分布极不均匀。然而，受限于建模复杂度和计算成本，目前面向城市复杂街区交通污染的数值模拟研究较为少见。部分学者针对榆中县城、马德里和首尔的实际街区［13-15］，采用CFD 数值模拟方法对一般道路的CO、NO2等气态污染物扩散进行了研究，分析了气态污染物在实际街区的扩散特性。因对道路结构的复杂性以及交通排放的动态性的考虑有所欠缺，未能真正反映高架桥、临街建筑结构和气象等综合因素影响下复杂街区内污染物的扩散情况。

综上所述，目前对交通尾气污染扩散的模拟研究大多集中在单一街谷型道路或简单街区的理想化模型，而实际街区流场分布及交通排放污染物扩散特性研究尚不完善。受高架桥道路、建筑物布局、风速风向等多重因素的综合作用，实际街区交通排放颗粒物的三维时空分布规律和演化特征不清且机理不明。因此，本文以含高架桥的实际街区为研究对象，构建街区场景模型，以实地监测数据作为输入，利用CFD 技术对实际街区中不同时段的交通颗粒物扩散进行研究，分析风向对街区流场和颗粒物分布的影响，并探讨了高架桥设置对于交通排放颗粒物扩散的影响，为降低城市居民污染暴露风险提供数据支持。

1 研究方法

1.1 实地监测实验

选取广州市人民高架路附近道路作为监测地点，图1为监测点位布设示意图。人民路为广州市城区的主干路，整体呈南北走向，所处街区建筑分布密集，高低不一，是城市复杂下垫面的代表。该街区位于广州市服装批发的繁华物流商圈，日间人流量大，地面交通拥堵情况较严重，机动车污染对街区的活动人群污染暴露有较大的影响。实验设置的观测点位于人民路南段，道路与两侧建筑物构成含高架桥的街谷型道路，道路宽20 m，监测点两侧建筑为不对称分布，分别约25 m和20 m，在距离地面1.5、7.7、11.5、15.6、20.3和25 m的垂直方向布设6个监测点位。

图1 实验观测点位分布Fig.1 The distribution of observation sampling points

实验在2017 年10 月29 日连续进行24 h 观测，颗粒物浓度测量采用Grimm 11-A 便携式气溶胶粒径谱仪，采样间隔为6 s，每个点位采集48 次，每次采样时间取90 s，按照点位顺序依次采集。实验同步采集交通流量数据及气象数据，交通数据通过视频录像机人工计数获取分车型的交通流量数据，气象数据通过广州市五中监测站获得，其距离实验点约1.5 km，该监测数据可代表实验点的气象情况，包含风向、风速、温度等。实验所采集到的数据如表1所示。

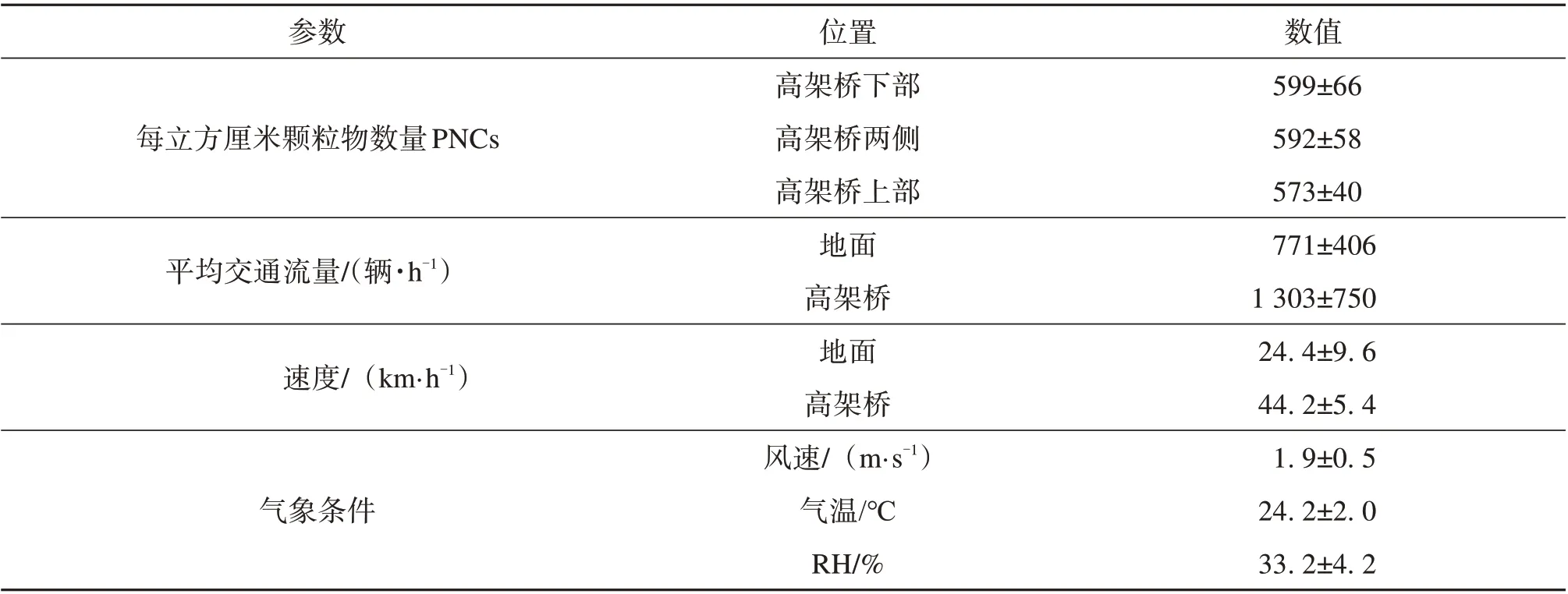
表1 交通、气象以及颗粒物污染情况Table 1 The traffic，meteorological and PNCs conditions

1.2 物理模型与计算方法

1.2.1 物理模型选取550 m×580 m 的含高架桥街区为研究对象，实际街区场景与三维物理模型如图2 所示。最高建筑物为80.5 m，最低为3 m；高架桥位于街道中央，高9 m，桥面宽10 m，高架桥两侧设置3 m 高的声屏障，计算域长、宽、高分别为1 000 m×1 000 m×500 m。由于实际街区的建筑物形状及分布不规则，采取结构化网格划分难度大，故采用非结构化四面体网格划分，高架桥壁面网格精度为0.2 m，建筑物壁面网格精度为1 m，总网格数约635 万个。实际物理建模过程中进行了两组网格划分，数量分别约为500 万和635万。模拟结果表明，两组网格中某截面上的平均风速相差小于1%，因此认为网格数已经达到网格无关，具备其独立性。本文选择网格数量为635万的模型作为分析依据。

图2 含高架桥实际街区的街景及物理模型Fig.2 Streetscape and physical model of the real built-up area with a viaduct

1.2.2 计算方法综合考虑计算效率、模型适用性以及模拟效果，本研究采用标准k-ε湍流模型计算流场［16-17］。其连续性方程为

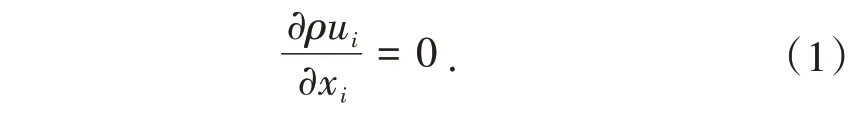
动量方程为

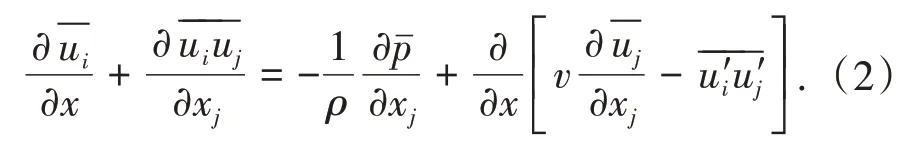
湍流动能传输方程为

湍流动能耗散率的传输方程为

式中ui和uj为空气流体平均速度在i和j方向上的分量，为雷诺平均应力，μ为层流粘度，μt为流体的粘度，μt=ρCμk2/ε，σk和σε分别表示湍流动能k和湍流动能耗散率ε对应的普朗特数，Gk为由于平均速度梯度产生的湍流动能，Gb表示浮力项的湍流动能，Sk和Sε为源项，Sk湍流动能源项考虑了道路车辆运动引起的湍流动能，YM代表在可压缩流动中湍流脉动膨胀对整体耗散率ε的贡献。式中 涉 及 的 常 数 分 别 取C1= 0.43，C1ε= 1.44，C2=1.9，C3ε= 1.44，Cμ= 0.09，σk= 1.0，σε= 2.2。

采用离散相模型描述和追踪颗粒物的迁移运动，颗粒物的瞬时运动由拉格朗日法计算。较多研究均采用该方法跟踪颗粒物运动轨迹［18-19］，获取颗粒物的浓度分布。将颗粒视为惰性污染物，不考虑颗粒之间的相互碰撞、成核及凝结等，颗粒物碰撞到壁面后将附着被捕捉，对粒径为2.5 μm（PM2.5）的颗粒物运动轨迹进行数值模拟。具体方程为

以上方程采用有限体积法求解，流场计算残差设定最大值小于10-6，控制方程的离散采用二阶迎风格式，压力和速度的耦合算法采用SIMPLE算法。在解域内追踪到总颗粒包裹变化数量及随机选取点的颗粒物浓度变化小于1%，视为达到稳定。

1.2.3 边界条件环境入口边界为速度入口边界，速度入口采用风廓线形式定义。出口边界为压力出口边界，计算域上边界采用对称边界条件，建筑壁面、高架桥壁面和地面为固体壁面边界。颗粒物移动至出口边界将逃逸出解域，颗粒物碰到壁面则被捕捉。风廓线符合指数形式

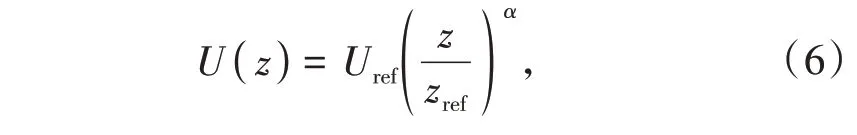
式中Uref为参考高度zref处的参考风速（m/s），α是风速高度指数，取0.22。定义监测站10 m 高度处风速为参考风速。

人民南路地面道路、人民高架桥道路及一德路均为双车道，机动车污染排放入射源设置为位于车道中心线两侧。和平东路为单车道，排放源设置为车道中心线，均为距离路面0.2 m 高的线源模型。基于实地监测实验获取的交通流量及车流速度数据，参照文献［20］的机动车排放因子，计算颗粒物入射强度

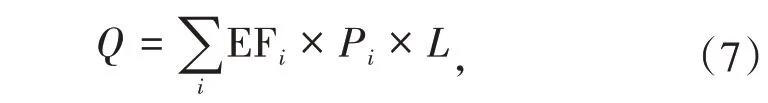
式中Q为线源颗粒物排放强度（kg/s）；EFi为排放因子（kg/（km·辆））；Pi为车流量（辆/h）；L为线源长度（km）。

对颗粒物浓度进行无量纲化处理，即

式中C为颗粒物质量浓度（kg/m3）；W为道路宽度（m）。根据实验采集的交通、气象等数据计算得到人民南路、人民高架路、和平东路以及一德西路共4 条道路24 h 的VIT 强度及排放量，如图3所示。

图3 实际街区不同时段的主要输入参数Fig.3 Main input parameters for different periods

2 分析与讨论

2.1 模型的验证

数值模拟的输入采用实验获得的风向、风速、交通等数据。时间序列上，选取行人呼吸高度处的颗粒物浓度与计算得到的24 h 浓度进行对比验证。由于该模拟缺乏背景浓度的输入，只能反映交通排放对实际街区颗粒物污染的影响，而实际场景中交通高峰时段交通排放较大，对实验点颗粒物分布的影响远大于背景浓度（其他排放源）的影响，因此本研究在空间上选取14：00 时段实验获取的颗粒物垂直分布与模拟的平均浓度分布进行对比验证。对两种方法得到的颗粒物浓度进行归一化处理，时间上以实验日各自颗粒物浓度的最大值为1进行归一化，空间上以行人呼吸高度（1.5 m）处的颗粒物浓度为1进行归一化，对比结果如图4所示。可以看出，模拟浓度在时间和空间上的变化趋势与实验结果较为一致，说明数值模拟方案能获得可靠的计算结果。

2.2 实际街区不同时段的流场及颗粒物分布

选择实验日14 时、15 时及23 时数值模拟结果为研究对象。由图4（a）可知，在14 时颗粒物污染最为严重。为了与14 时进行对比，选择交通排放相当但风向相差较大的15 时以及风向条件较为一致但交通排放小的23时进行讨论。3个时间段的风向风速及交通排放量如表2 所示，14 时与15 时为实验日交通排放量较大时段，风向分别为北风和东北风，风速接近。14 时与23 时风向风速情况基本一致，但23时为夜间，交通排放较少。

表2 不同时段的风向、风速及交通排放量Table 2 Wind conditions and traffic emissions during different periods

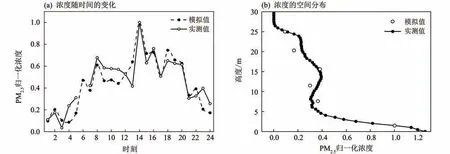
图4 颗粒物浓度的计算结果与实验数据Fig.4 Numerical results and observation data of particle concentrations

2.2.1 街区流场分布图5（a）～（d）为14 时与15时水平方向及垂直截面上的空气流场分布情况。水平分布（Z= 1.5 m）上，14 时流场在含高架桥的街道中部风速较小；交叉口附近通风良好，流线自街谷向交叉口外延伸，有利于街谷内污染物外向扩散。15 时与14 时流场分布整体差异较小，但局部区域流场分布对风向扰动的响应十分敏感，其中15时交叉口处风速较14时低且15时流场方向为自南向北。在B1-B1截面处，14 时为下部向低矮建筑物上方发展，在高架桥附近形成两个较小漩涡，风速较小。15 时与14 时的流线发展方向差别较大，15 时是自低矮建筑物向高架桥底部发展，高架桥底部风速明显较14 时高，扩散条件较好。虽然14 时与15 时风向仅相差9.5°，但局部区域的流场分布存在明显差异，复杂街区入流风向较小的扰动对其流场分布的影响显著。

图5 街区内不同时段的流场分布Fig.5 Distributions of flow field in the built-up area during different periods

2.2.2 街区颗粒物浓度分布图6（a）～（f）分别为14 时、15 时及23 时在行人呼吸高度及B1-B1截面的颗粒物浓度分布。整体上三个时间段交通排放颗粒物均聚集在街道中段，该区域的来流风受到街区密集建筑物的遮挡难进入街谷内，导致街道中部风速较低，颗粒物难以扩散，从而形成高污染区。B1-B1截面处，14时与23时高架桥底部风速低，地面排放的颗粒物难以扩散，均随气流向低矮建筑侧堆积，而14 时较大的交通排放量更导致整个街谷内受到颗粒物严重污染。15 时与14 时颗粒物垂直分布差异大，15 时的高架桥底部风速较大，地面颗粒物得以扩散，颗粒物较少输送至建筑物两侧，整体污染浓度明显较14 时小。结果表明：城市街区的街道中部通风条件差，即使交通排放量较小，颗粒物仍会不断积累，易造成污染。

图6 街区不同时段的颗粒物浓度分布Fig.6 Distributions of DPM*in the built-up area during different period

2.3 风向对街区流场及颗粒物浓度分布的影响

实际街区结构的复杂性，环境风向的改变会影响街区不同位置的流场分布，包括涡流的形成、影响范围等，更进一步会影响颗粒物扩散、积累等，产生不同的颗粒物浓度分布。2.2 节的模拟结果也表明颗粒物的扩散受来流风向扰动影响较大，风向的小幅扰动（9.5°）会显著改变颗粒物水平和垂直方向分布情况。因此，需进一步探究风向变化对流场及颗粒物浓度分布的影响。本节主要讨论风向为北风和东风时，在平均风速2 m/s 的条件下，风向对街区沿线以及高架桥附近垂直方向的流场与颗粒物浓度分布的影响。

2.3.1 流场的三维模拟结果排放强度以实验监测的交通高峰期时段为恒定输入。图7为不同风向下街区内流线的三维空间分布。

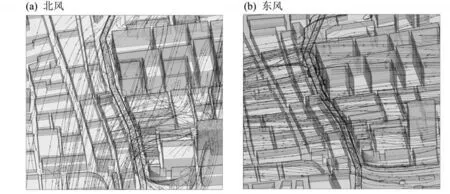
图7 不同风向下空气流线的三维分布Fig.7 Three-dimensional distributions of air streamlines with different wind directions

北风时，来流风近似平行于含高架桥的街谷。受建筑物和街道拐角的作用，进入建筑物上部时稍向东侧偏转，并自北向南在高架桥底部及桥面流入街谷；而部分气流受到交叉口附近高大建筑物的影响，气流流向直接发生改变，偏转为东侧气流进入街区的街谷内，围绕高架桥形成逆时针垂直涡流，在高架桥底部从迎风面流向背风面。

当朱利安思考回归家庭，另一位“大师班”学生则在宁夏酿酒酿得不亦乐乎，他就是大陆MW最年轻的申请者——戴鸿靖（Ian）。今年，戴鸿靖换了个狂野不羁的发型，颇有没睡醒的爱因斯坦风范，从此他有了个新代号“Ian·斯坦·戴”。今年他还酿出了很好玩的酒，在朋友圈里不无自豪地表示：“距离中国最好，还很遥远。距离中国最好玩，那是不太远了！本年度中国酿造最好玩的葡萄酒，不服来战。”

东风时，来流风垂直于含高架桥的街谷，交叉口处及建筑物上部受建筑物影响较小，流场方向与来流风一致。来流风在街谷的中部绕高架桥流动，而在交叉口处流线则向街谷内发展，部分绕高架桥从西侧流出，未形成垂直涡流。可见来流风向的改变直接影响街区内气流的流向变化，使得同一位置的湍流结构（包括涡流数量、位置等）有较大改变。

2.3.2 街区沿线流场与颗粒物浓度分布不同风向下，街道峡谷内、交叉口处以及高架桥附近颗粒物扩散条件有显著差异。不同风向下，行人高度处（Z= 1.5 m）的流场及颗粒物分布如图8 所示。北风时，来流风近似平行于含高架桥的街谷，机动车排放的颗粒物主要聚集在街道峡谷的中段，而街谷南、北段颗粒物的浓度则较低，下降了约66.7%。这与该风向下街谷内流场的分布情况相符，街谷中段存在一片低风速区，导致颗粒物在该区域不断累积。研究表明［11］，在平行风下街道峡谷中的污染物很容易扩散出去，难以在街谷中形成较高浓度的污染。在本研究中，虽然街谷的走向与北风向较为接近，但是街谷的北段（上风向）存在30°左右的拐角，影响了风场继续向下游传播，并导致街谷中段形成低风速区，影响颗粒物的扩散。这说明街道峡谷中的拐角是影响街谷内污染物扩散的不利因素，应尽量避免。

东风时，来流风向与街谷走向接近垂直，颗粒物在街道峡谷的中段附近聚集效应增强。与北风时不同的是，东风下街谷中段右侧的通风走廊起到了一定作用，使得走廊位置处形成一小片低浓度区。据田丰等的研究［21］，在垂直风下理想的街谷型交叉口外侧气流在街谷内形成垂直涡旋，污染物在背风面堆积。在本研究中，虽然街谷整体走向与东风近似于垂直，但十字交叉口的东南方向建筑物稀疏，迫使东侧来流风向西侧及北侧街谷内流入，使得北侧街谷靠近入口的路段形成平行风，排放污染物沿道路方向扩散，未向两侧建筑输送。这对于街谷附近的居民健康是非常有利的。因此，可通过对交叉口附近建筑的布局进行合理设置，引导风场进入街道峡谷内部，稀释交通排放的颗粒物浓度。

交叉口处（Y= 133 m） 延伸至街谷内部160 m 范围内街谷两侧的颗粒物浓度，如图8（c）和（f）所示。背风面（建筑物旁）颗粒物浓度在北风下沿交叉口至街谷内呈线性上升，至街谷内100 m处颗粒物无量纲浓度约为交叉口处的3.4倍；在东风下，距离交叉口0～100 m范围内建筑物附近颗粒物浓度极低，甚至低于交叉口处浓度，在大于100 m的范围内颗粒物浓度急剧增加至北风下相同位置的浓度水平。这是由于通风较好交叉口的设置使得垂直风能从交叉口延伸至街谷内，街谷边缘处形成风速较高的平行风，提高了颗粒物的扩散效率。迎风面在两种风向下的颗粒物浓度则较低，均与交叉口处浓度接近。综上，无论在平行风（北风）还是垂直风（东风）下，整个街区中排放较大的都在含高架桥街道峡谷内，较少扩散至街谷外的建筑区域，而该街道中部的风速约为0.45 m/s，形成低速区，导致街谷中部的颗粒物污染最为严重。

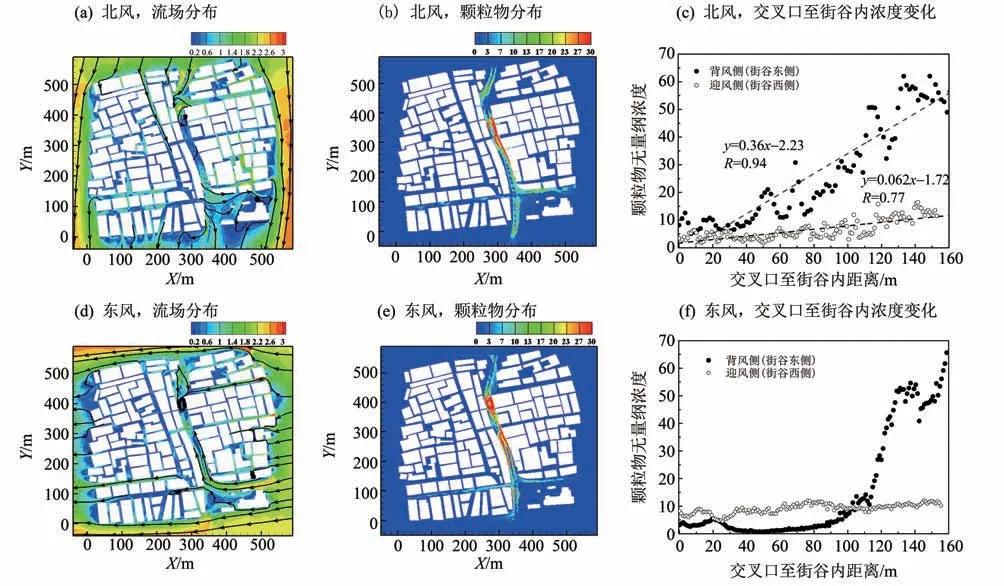
图8 不同风向下的流场及颗粒物无量纲浓度分布Fig.8 Flow field and normalized particle concentration distributions in different wind directions

2.3.3 沿垂直方向流场与颗粒物浓度分布以污染严重的含高架桥街谷区域为研究对象，选取不同的纵向截面（即图2 中6 个截面），得到街道不同位置沿该垂直剖面的流场及颗粒物分布。建筑群的高低组合形成非对称街谷，街谷形状对内部气流运动及污染物分布有明显影响［22］，为衡量不同截面建筑物组成的街谷形状，将街谷建筑形状因子λ定义为街谷内较高建筑物高度H1与较矮建筑物高度H2的比值。

图9（a）～（c）为北风下λ= 1.1～1.3 时靠近交叉口街谷内的不同截面流场及颗粒物分布。如图9所示，A1-A1和A2-A2截面为下阶梯型街谷，街谷内主要形成一个绕高架桥逆时针旋转的大涡流。涡流作用下，排放的颗粒物在地面和背风面堆积，高架桥排放源导致街谷中部浓度升高，而迎风面颗粒物浓度最低。其中，由于A1-A1截面两侧建筑物更高，高架桥阻挡作用更为明显，高架桥上部至背风面形成低风速区，平均风速仅0.4 m/s，扩散条件差，使得背风面高架桥旁的位置有少量颗粒物积累，浓度随高度增加呈现先减后增的趋势。A3-A3截面为上阶梯型街谷，受高架桥结构影响，在高架桥的下部和东侧形成涡流，大涡流的中心较一般街谷的涡流高度显著降低［18］，风速较低，地面附近颗粒物污染严重。有研究表明［23］，无高架桥的上阶梯型街谷中，颗粒物在背风面有显著的爬墙效应并向下游建筑扩散，与本研究A3-A3处的颗粒物分布明显不同。本研究中由于高架桥的存在，地面产生的颗粒物受到阻挡，仅在高架桥下堆积，背风面颗粒物的爬墙效应被破坏，而桥上排放的颗粒物向下游建筑物有一定扩散。

图9 北风下不同截面的流场及颗粒物无量纲浓度垂直分布Fig.9 Vertical distributions of section flow field and normalized particle concentration under north wind

图10 北风下B-B截面流场及颗粒物无量纲浓度垂直分布Fig.10 Vertical distributions of B-B section flow field and normalized particle concentration under north wind

图11（a）～（c）为东风下λ= 1.1～1.3 时不同截面的流场及颗粒物分布。东风下，气流从交叉口进入街谷边缘处，使得交叉口附近的街谷内通风条件良好，平均风速达北风时的1.9 倍，A1-A1、A2-A2和A3-A3截面均未形成大涡流。A1-A1和A2-A2截面的地面排放颗粒物受到平行于街道气流的显著影响，颗粒物未向两侧建筑物堆积，一部分在排放源附近小范围积累，一部分随气流沿街道扩散。距离交叉口较远的A3-A3截面处，地面及高架桥上部风速显著降低，受垂直风影响大，地面及高架桥上颗粒物未能向外扩散，整个截面颗粒物污染区域占比大。因此，与2.3.2节一致，交叉口处建筑物的合理布局有利于引导垂直风进入街道峡谷内部，在街谷内入口路段形成平行风，极大改善了垂直风下污染物难以扩散的情况。

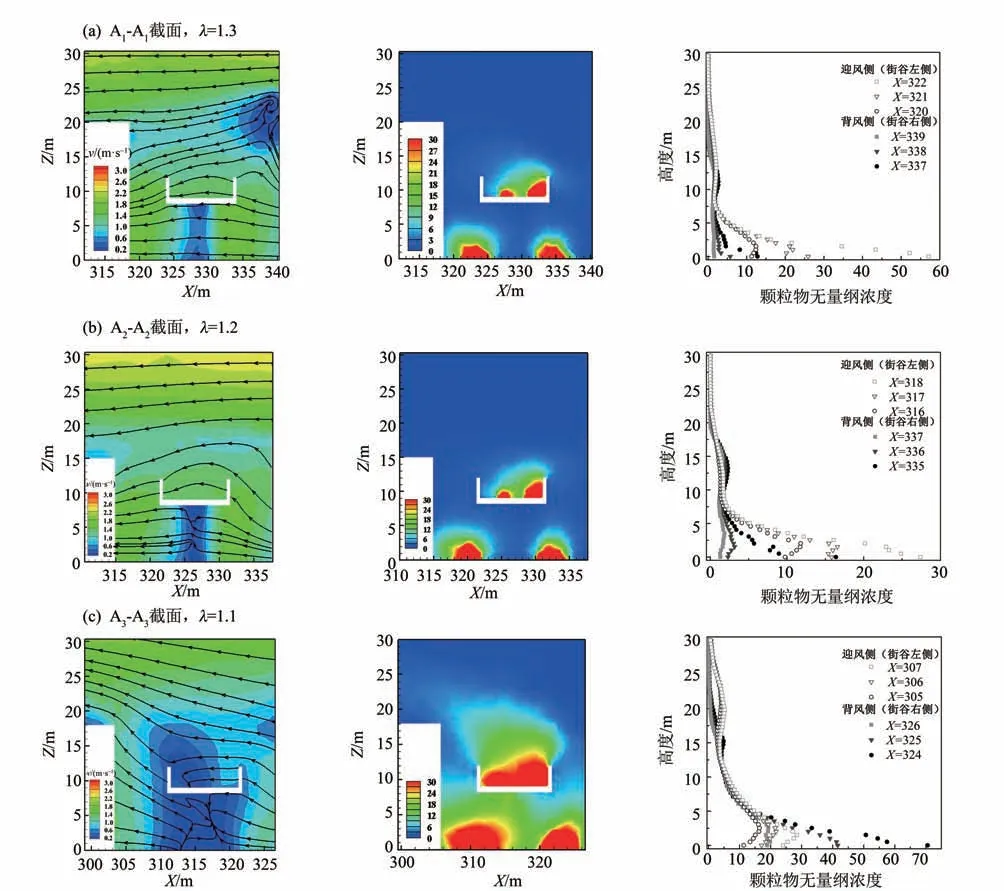
图11 东风下A-A截面的流场及颗粒物无量纲浓度垂直分布Fig.11 Vertical distributions of A-A section flow field and normalized particle concentration under east wind

图12（a）～（c）为东风下λ= 2.7时不同截面的流场及颗粒物分布，B1-B1和B3-B3截面的街谷内形成较大范围的逆时针漩涡，由于街谷建筑形状因子较大，其漩涡较λ= 1.1～1.3 截面（图9）向下游建筑延伸，漩涡中心也偏移至下游建筑物上部，并经过下游建筑物屋顶延伸至尾流区，与杨方等［22］研究中λ= 7 的理想不对称街谷流场分布相似。街谷内背风面建筑物高，来流风不易进入，使得高架桥上部区域整体风速偏低，桥上污染物扩散条件差，颗粒物浓度明显增高。漩涡的偏移，使得桥上颗粒物受涡流明显作用，被带至背风面，进一步加重了街谷上部污染，B1-B1截面背风面建筑上部颗粒物浓度更增长至与地面浓度接近，最高达行人呼吸高度颗粒物浓度的84.00%，较北风下同位置颗粒物浓度高出一个量级。在高架桥底部，由于B3-B3截面位于弯道处，部分东侧来流风偏转，从高架桥上部进入弯道处底部，造成颗粒物在迎风面堆积，形成B3-B3迎风面下部颗粒物浓度显著增高，约为其余两个截面的2.2倍。东风下，较大的街谷内颗粒物整体污染严重，背风面与迎风面颗粒物的垂直分布受到高架桥上排放源影响大，在高架桥上部可能出现突增或保持较高的浓度水平。

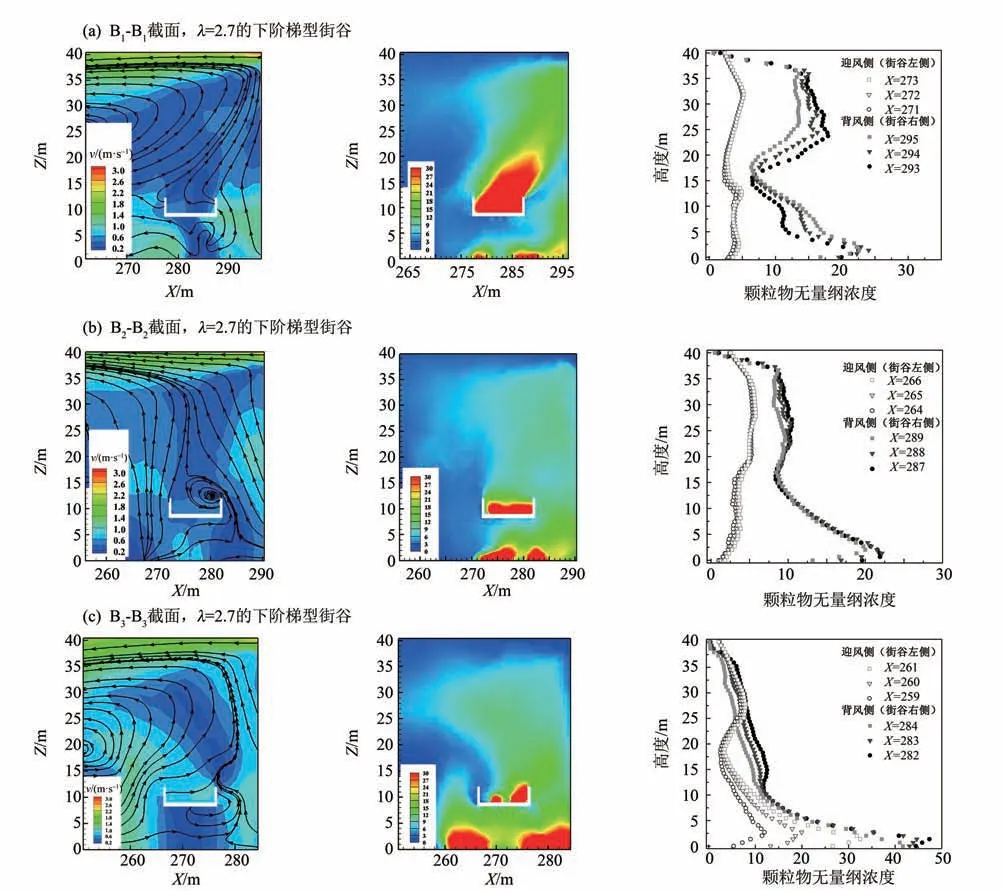
图12 东风下的截面流场及颗粒物无量纲浓度垂直分布Fig.12 Vertical distributions of section flow field and normalized particle concentration under east wind

综上所述，受建筑物布局、形状、高架桥布设、街道位置等因素的影响，不同的边界来流风向对实际街区流场方向和风速的影响存在区域差异，并导致不同位置颗粒物垂直分布差异大，背风面颗粒物在不同高度处可能出现突增情况。受高架桥遮盖作用［10］，地面排放颗粒物容易堆积，背风面下部颗粒物污染最为严重。建筑物两侧距离高架桥不同位置处颗粒物垂直分布规律较为一致，高架桥下部浓度差异较大。

3 结 论

本文以广州市含高架桥实际街区为例，利用实测数据模拟了不同时段空气流场和颗粒物分布，与实验测量结果较为一致，并考察了不同风向对流场及颗粒物扩散的影响。结果表明：

（1）实际街区内高大建筑物的存在会改变来流风方向，街区不同位置风向和风速对来流风向变化的响应存在明显差异，而颗粒物的扩散受来流风向扰动影响较大，风向小幅的扰动（9.5°）也会显著改变颗粒物水平和垂直分布情况。

（2）实际街区流场和颗粒物分布存在明显空间异质性，街道的弯道存在会阻碍来流风进入，即使在平行风下，弯道仍显著影响风场向下游传播，导致街谷中部形成低风速区，颗粒物污染最为严重。

（3）街区十字交叉口的东南方向建筑较少的设置，迫使东侧入流风（近似垂直风）分别进入北侧及西侧街谷内，使得北侧街谷的交通颗粒物仅分布在道路中间，不向街谷两侧输送，有效降低了临街行人与居民的污染物暴露浓度。

（4）高街谷建筑形状因子下，当来流风平行于街道时，靠近街区来流入口的高层建筑仍有滞留效应，颗粒物在该侧不同高度处有不同程度的聚集；当来流风垂直从高层建筑进入时，街谷内高架排放源对两侧颗粒物垂直分布影响极大，使得颗粒物在高架桥上部出现明显突增或保持高浓度水平，最高达行人高度处颗粒浓度的84%，并比平行风时同位置浓度高出一个量级。

（5）高架桥对实际街区不同街谷内流场和颗粒物分布的影响存在差异。在垂直入流下，下阶梯型街谷中，高架桥使得涡流中心抬升至高架桥上部，背风面颗粒物垂直分布有明显爬墙效应；上阶梯型街谷中，涡流中心被压至高架桥底部，颗粒物在高架桥下方堆积，未被带至背风面上形成滞留。