人工源极低频电磁波场空间分布的计算

杨 静 陈小斌 赵国泽

1)山西省地震局，临汾地震监测中心站，临汾 044400

2)应急管理部国家自然灾害防治研究院，北京 100029

3)中国地震局地质研究所，北京 100029

4)太原大陆裂谷动力学国家野外科学观测研究站，太原 030025

0 引言

大功率人工源极低频电磁波技术(Controlled Source Extremely Low Frequency Method，CSELF)是近年来电磁地球物理领域发展起来的新技术(Galejs，1972；Perteretal.，1973；Antonyetal.，1998；赵国泽等，2003a，2010，2012；卓贤军等，2004，2007)，该技术的最大优势是利用很长的发射天线(数十至上百千米)和较大的发射电流(数百安)(赵国泽等，2003b，2010；陈小斌等，2009)，可发射出强大稳定的电磁波，覆盖范围达数百万平方千米，能应用于地震监测、地下资源勘察、海洋和近地空间研究等领域。在国家“十一五”重大科技基础设施建设项目“极低频探地工程”的支持下，中国建立了30个人工源极低频电磁场固定观测站，用于监测地震电磁前兆异常信号及地下电性结构变化(赵国泽等，2003b，2010，2012；Ohtaetal.，2013；张学民等，2017)。

CSELF在电磁波的产生、传播及空间分布特征等方面与常规可控源电磁法有着很大不同。空间分布的交变电磁场存在感应场和辐射场2种形式。感应场是由一次场在有耗媒质中感应所生，主要依靠传导电流传播，可用似稳场理论描述；辐射场则是在一次场的激励下，交变电磁场在电介质中由电场、磁场相互转换而产生，主要依靠位移电流传播，可用波动场理论描述。CSELF电磁波中既包括感应场又包括辐射场，其空间传播区域可划分为近区、远区和波导区3个区域。在近区和远区，CSELF电磁波主要表现为感应场形式，可忽略位移电流以及电离层和地球球形结构带来的影响，传播特征可用似稳场理论描述，与经典CSAMT电磁测深理论一致；在波导区CSELF电磁波则主要表现为辐射场形式，可忽略传导电流的影响，依靠位移电流进行传播，且必须考虑电离层及地球球状结构的影响。

已有不少学者对CSELF技术的理论和应用等方面开展了相关研究。赵国泽等(2003b，2010，2012)归纳总结了多次CSELF野外试验结果和数据处理技术，展示了CSELF在地球物理研究中的巨大应用潜力。卓贤军(2005)给出了地球模型波导区近似解等计算结果。底青云等(2008)、李帝铨等(2010)研究了水平层状模型下CSELF大尺度源的求解及其影响，对可控源电磁波的响应特征进行了分析。徐志锋等(2010)求解了电离层-大气层-地球谐振腔模型的解析解，研究了与天线垂直方向上CSELF场的分布特征。徐维东等(2016)和程东(2017)应用卫星观测到的VLF电场数据计算了甚低频VLF电场的空间传播特征。王元新(2007)和王元新等(2008)求解了波导区的电磁场，但其主要针对通信领域。以上这些研究均未在电离层-大气层-地球谐振腔模型下完整且详细地讨论CSELF电磁波等各个分量在不同分区的计算理论及其空间分布特征。

本文将对CSELF电磁波场在近区、远区和波导区的空间分布特征展开讨论。在查阅已有研究文献的基础上，对CSELF不同空间分布的理论计算公式进行了归纳、整理、推导和验证，研发了可视化计算软件，在不同坐标系下分析讨论了CSELF电磁波的空间分布特征，为CSELF的应用提供了较为全面的理论和计算支持。

1 理论基础及计算实现

人工源极低频电磁波在近区、远区和波导区的传播方式不同。在近区和远区为似稳场，本文基于均匀半空间水平电偶极子模型，从经典频率域可控源电磁理论出发，归纳整理并重新推导验证了似稳场的计算公式。CSELF在波导区为辐射场，文中借鉴通信领域的研究成果，基于球形谐振腔模型，给出了波导区的近似计算公式。

1.1 似稳场的解

设定均匀半空间模型：水平电偶极子源的中心位于柱坐标原点，沿X轴方向放置(φ=0)，Z轴向下(指向地心)，如图1 所示，其中下半空间(xy平面以下的部分)代表大地，上半空间(x轴以上的部分)代表空气。假设偶极子源中的电流为I，偶极距为dx，则似稳场的精确解为(何继善，1990；卓贤军，2005)

(1)

(2)

(3)

(4)

(5)

(6)

图1 柱坐标系下均匀半空间模型表面的水平电偶极子源Fig.1 Horizontal electric dipole source on the surface of a uniform half-space model in a cylindrical coordinate system.

1.1.1 近区场近似解

当r值较小且满足|k0r|≪1、|k1r|≪1时，在z=0+处，修正Bessel函数In、Kn和指数函数用渐近级数的前2项或前3项替代，可得到场强的近似表达式，通常被称为近场公式(何继善，1990；卓贤军，2005)：

(7)

由近区场公式可以看出，在均匀介质表面，水平电偶极子源的近区场中电场水平分量正比于介质的电阻率，与频率无关；电场垂直分量与频率成正比，而与介质的电阻率无关；所有磁场分量强度与频率和介质的电导率均无关。

1.1.2 远区场近似解

当r值较大且满足|k0r|≪1≪|k1r|时，在z=0+处，修正Bessel函数In、Kn用渐近级数展开项的第1项和第2项替代，且e-k1r项近似为0，则可得到场强的近似表达式，通常被称为远场公式：

(8)

由式(8)可见，在远区，水平电偶极子源的电场水平分量正比于介质的电阻率，而与频率无关。而磁场水平分量与频率和电导率乘积的平方根成反比，垂直分量与频率和电导率的乘积成反比。

1.2 波导区场近似解

当极低频电磁波的传播距离超过一定范围后，由于有耗媒质中能量的损耗，通过地球内部以传导电流传播的部分和以地面滑行波传播的部分逐渐可忽略不计，CSELF波进入波导区，依靠位移电流进行传播。本文借鉴通信领域波导区的近似解公式(Harrison，1974)，考虑地球曲率的影响，在球形谐振腔模型(图2)下计算波导区的电磁场。

图2 地球-大气层-电离层球形谐振腔模型示意图Fig.2 Schematic diagram of the earth-air-ionosphere spherical cavity model.

如图2 所示，水平电偶极子源放置于ρ=0，φ=0，r=a处，场点坐标为(ρ，φ，a)，则场分量的近似表达式为(Harrison，1974)

(9)

式中，坐标原点o为地心，a为地球半径(m)，hi为电离层高度(m)，ρ为源点至场点的大圆弧长(取小距离)(m)，φ为穿过源点和场点大圆的方位角，dx为水平电偶极子天线的长度(m)，c为自由空间的光速(m/s)，v为电磁波在波导区中的传播速度(m/s)，α为电磁波在波导区的衰减率(Np/m)，Er和Hφ分别为波导区中传播的电场(mV/km)和磁场(nT)。

1.3 视电阻率的定义

本文将利用视电阻率验证计算结果的准确性。频率电磁测深中，视电阻率的定义最初来自大地电磁测深(MT)理论。在MT中，场源可近似为平面波入射到地面，由此引入波阻抗Z，表征地球电性分布对大地电磁场的响应(Tikhonov，1950)：

(10)

为了能够直观地定性分析地下介质的电阻率值，将波阻抗转换为视电阻率，卡尼亚视电阻率的定义为(Cagniard，1953)

(11)

由式(11)可知，卡尼亚视电阻率与垂直分量无关，因此无法验证垂直分量的计算是否准确。为验证其准确性，根据远区场电磁场垂直分量的近似计算公式，分别定义垂直分量的视电阻率为

(12)

(13)

1.4 可视化计算软件的实现

在以上计算公式的基础上，基于面向对象技术，利用Delphi研发了人工源极低频电磁波场计算程序，实现了似稳场精确解及近区近似解、远区近似解和波导区近似解的计算。该计算程序支持3种主要坐标系(直角坐标系、柱坐标系和球坐标系)，可快速对计算结果进行可视化显示，非常便于使用。

为统一极低频电磁波在空间中的传播计算，在软件设计过程中将似稳场解的传统坐标系转换到极低频通信领域惯用的z轴由地心指向外的坐标系。

2 结果分析

为便于结果的分析与讨论，参考大功率人工源极低频项目的信号发射参数，设计如下理论计算模型：发射天线的电偶极矩(Idx)为107A·m，发射频率为100Hz，大地电阻率为2000Ω·m，场点位于地表。

2.1 似稳场的计算与衰减特征

2.1.1 计算结果的验证

本文中计算软件本身的设计过程也较为复杂，故计算结果的正确性验证颇为重要。由于均匀半空间模型的视电阻率即为模型本身的电阻率，故本节采用视电阻率值对比的方法验证上述理论计算公式和程序设计的正确性。

首先使用卡尼亚视电阻率来验证近区、远区水平电磁场分量的正确性。计算时，利用近区近似解、远区近似解及似稳场精确解分别获得视电阻率，结果如图3 所示。在远区，电磁波可视为平面波，满足大地电磁的理论要求，由图3 可见，求得的卡尼亚视电阻率的值为2000Ω·m，与理论模型相同，表明远区近似解是正确的。似稳场的精确解在近区不满足平面波条件，求得的视电阻率误差较大，但进入远区后，求得的视电阻率逐渐逼近2000Ω·m，最后重合，表明似稳场水平分量的精确解求解公式是正确的，近区近似解在距离较小时与似稳场的精确解相同，证明近区场水平分量近似解的计算也是正确的。由此，通过卡尼亚视电阻率的对比，我们验证了本文中水平分量的近区场近似解、远区场近似解和似稳场精确解的计算均是正确的。

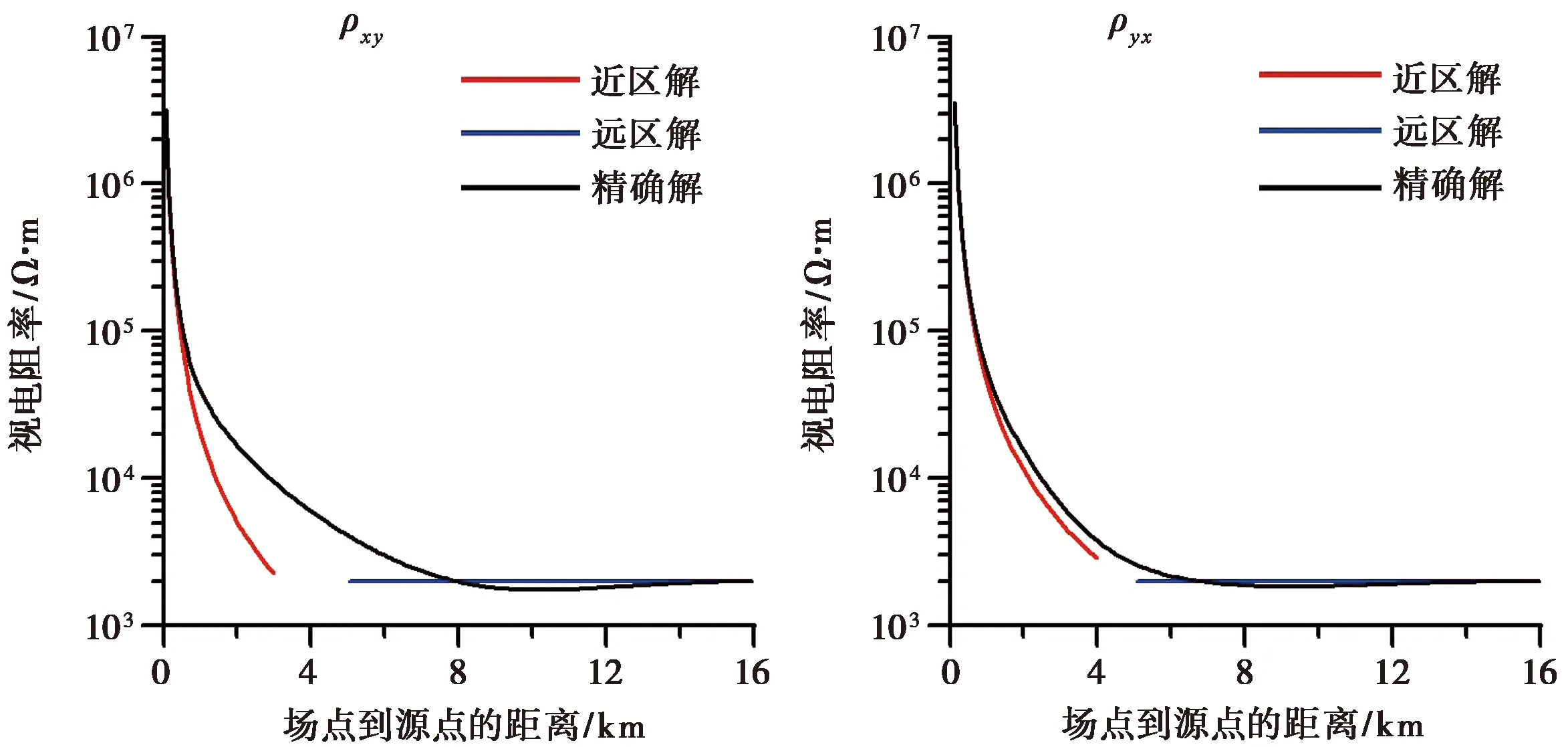
图3 卡尼亚视电阻率的计算结果Fig.3 Calculation results of Cagniard apparent resistivity.计算参数：Idx=107A·m，f=100Hz，ρ=2000Ω·m

同理，利用垂直分量定义的视电阻率的计算结果如图4 所示，可知本文中垂直分量的近区场近似解、远区场近似解和似稳场精确解的计算也是正确的。

图4 垂直分量定义的视电阻率的计算结果Fig.4 Calculation results of apparent resistivity defined by vertical component.计算参数：Idx=107A·m，f=100Hz，ρ=2000Ω·m

2.1.2 似稳场的衰减特征

图5 给出了CSELF在近区、远区时电磁场随距离的衰减关系。从该图可以看出，频率为100Hz的CSELF电磁场在此空间范围内随距离的衰减非常快，从源附近几十米至距离源十几千米的范围，场强均衰减了4个数量级以上，其中Hz分量的场强衰减达8个数量级，这说明感应场的影响范围较小。

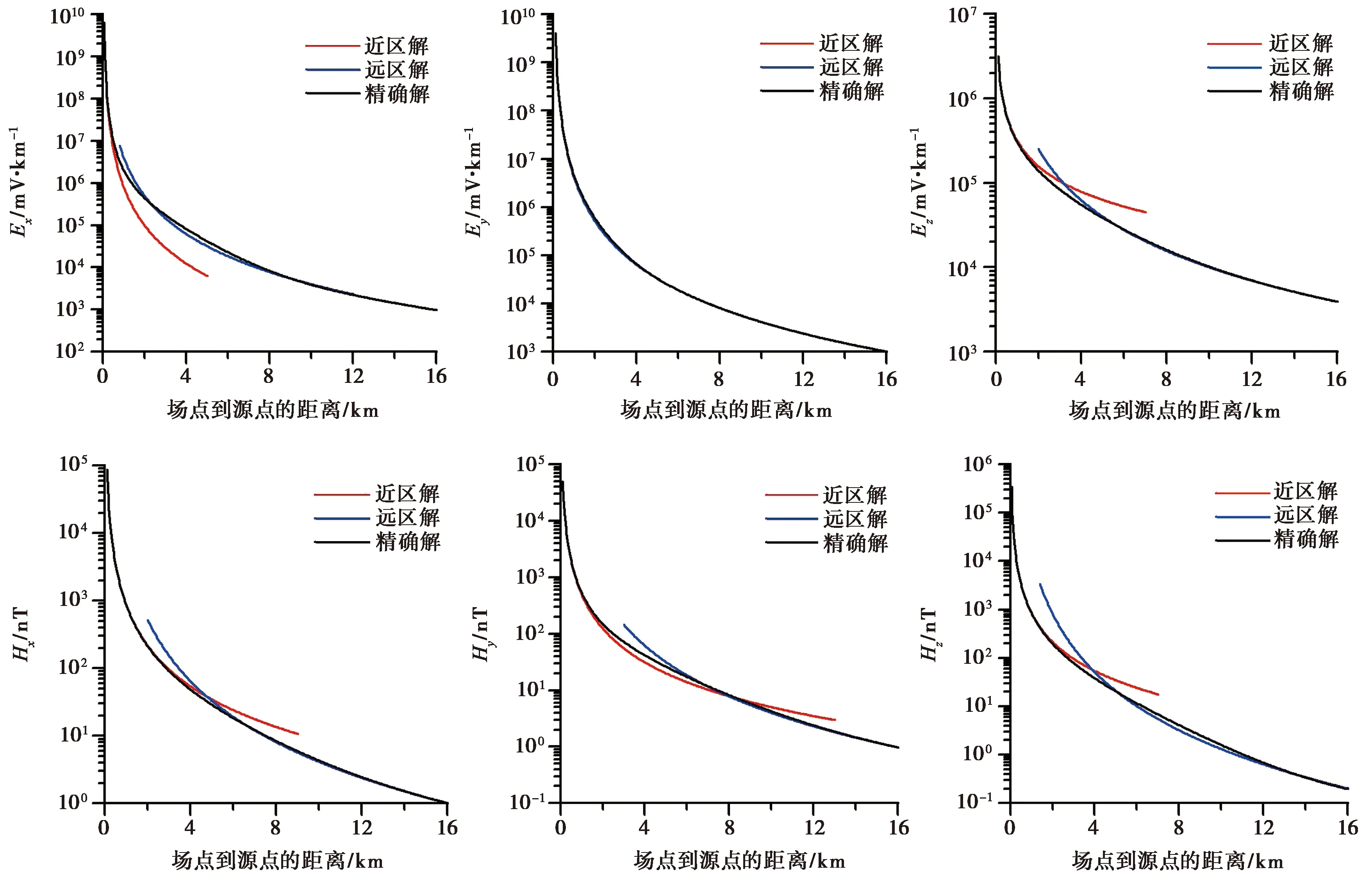
图5 近区、远区CSELF电磁场的衰减及计算结果的对比(φ=60°)Fig.5 The attenuation and calculation results of CSELF EM field in near and far zones.计算参数：Idx=107A·m，f=100Hz，ρ=2000Ω·m，φ=60°

图5 同时展示了近区近似解、远区近似解以及似稳场精确解的衔接过渡关系。近区场、远区场的衔接是电磁波能否近似为平面波的分界。从图5 中可以看出，在近区和远区之间存在一定的过渡区，在过渡区内近区、远区的近似解相交。在近区、远区内，近似解均与精确解结果相重合，而过渡区中，近区、远区的近似解与精确解均有所偏差，且不同场分量的过渡区范围不相同。目前在科研和生产工作中，CSAMT方法主要利用远区进行测量，将近区和过渡区弃用，造成了很大的能源和探测空间的浪费。

2.2 波导区电磁场的计算与衰减特征

按照通信领域的计算经验，取波导区的计算参数为：电离层的高度为85km，衰减因子为7.812Np/mm，光速与波导区中的电磁波速度比为1.25。

图6 波导区的CSELF电磁场随距离的变化(φ=45°)Fig.6 Variation of CSELF EM field in waveguide zone with distance(φ=45°).

根据式(9)计算的波导区场的结果如图6 所示。从图中可明显看出，在源区场强最大，传播过程中电磁场的衰减很慢，不到1个量级，经过一段距离衰减后又开始增大，传播到对极点后场强又会达到一个极大值，反映了球形谐振腔波导区电磁波特有的区别于水平层状地球的干涉增强特性，这一特征与Barrick(1999)的计算结果相同。

2.3 远区、波导区的过渡与衔接

图7 显示了远区场的近似解与似稳场的精确解在离源较近的远区完全重合，并随着距离的增大而迅速衰减。由远区与波导区的衔接可知，在200km范围内，远区场的衰减有5、6个级次；相对而言，波导场的衰减很慢，衰减量不到1个级次。对于电场，远区场在约120km处与波导区场相交；对于磁场，远区在约230km处与波导区相交。因此，当距离超过230km后，电场和磁场均满足波导区条件，电磁波开始在波导区中传播。从这里也可以看出，电场比磁场更早进入波导区传播。

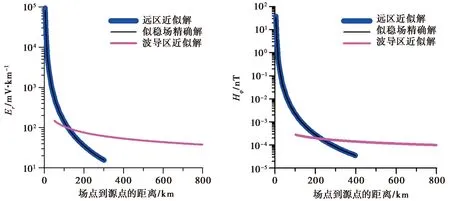
图7 CSELF远区场与波导区场的对比(φ=45°)Fig.7 Comparison of CSELF EM field in far and waveguide zones(φ=45°).

2.4 不同坐标系下似稳场的空间分布特征

为直观地展示似稳场电磁波在空间的分布特征，采用本文研发的计算软件分别计算了直角坐标系、柱坐标系和球坐标系下似稳场各个场分量的场强辐射花样图，计算参数同上：Idx=107A·m，f=100Hz，ρ=2000Ω·m。从结果图(图8—10，图中色标值为电磁波场强的对数表示，电场场强单位为mv/km，磁场场强单位为nT)中可以看出，在不同坐标系下，场的空间分布状况差别很大，辐射花样完全不同。

图8 直角坐标系下均匀半空间模型的CSELF电磁场空间分布图Fig.8 Spatial distribution of CSELF EM field of uniform half-space model of Cartesian coordinate system.

图9 柱坐标系下均匀半空间模型的CSELF电磁场空间分布图Fig.9 Spatial distribution of CSELF EM field of uniform half-space model of Cylindrical coordinate system.

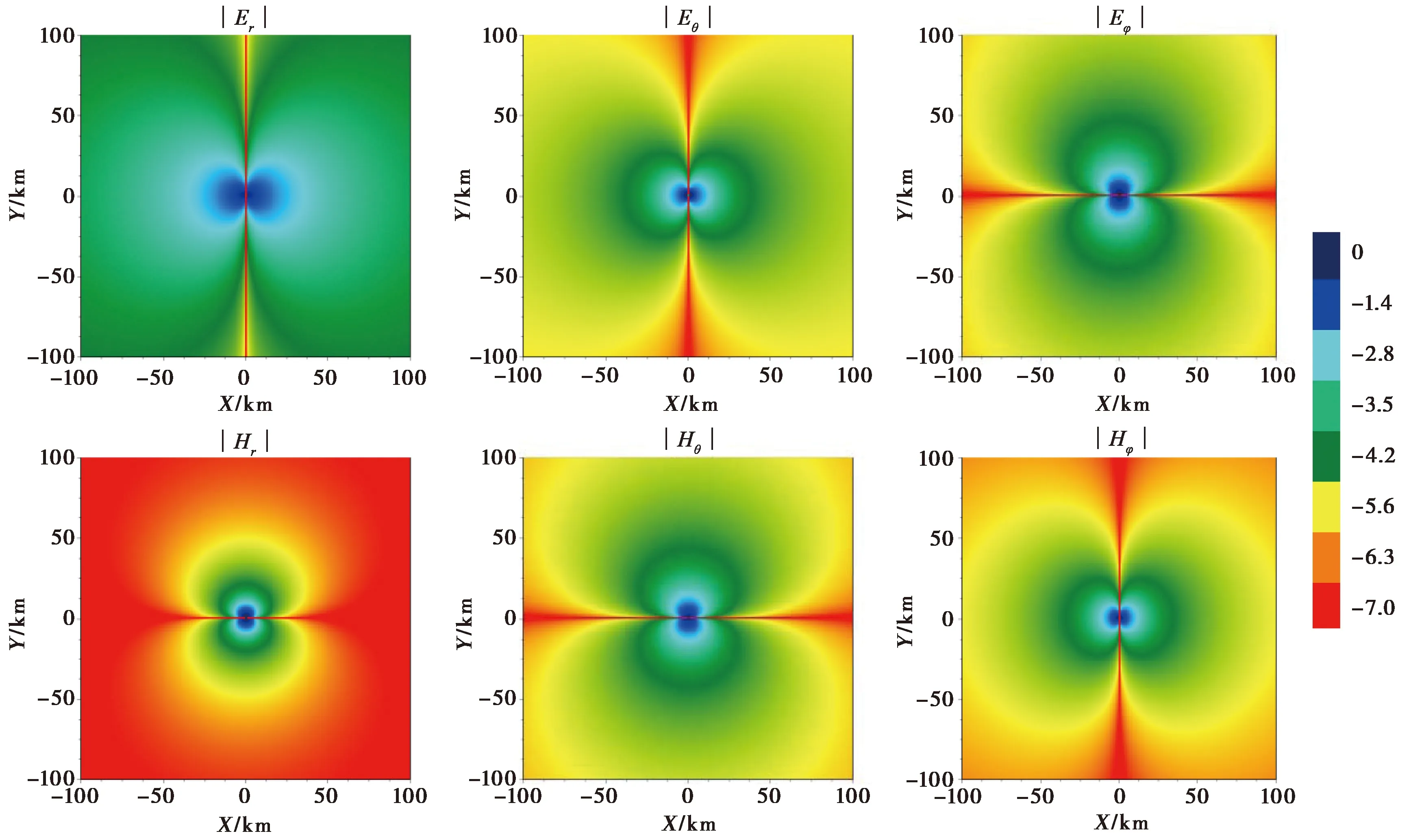
图10 球坐标系下均匀半空间模型的CSELF电磁场空间分布图Fig.10 Spatial distribution of CSELF EM field of uniform half-space model of spherical coordinate system.

图8 显示，在直角坐标系下，4个水平场分量在远区呈现为四象限分布特征，Ex分量与Hy分量的空间分布形态接近，Ey分量与Hx分量的空间分布形态接近，与电磁理论中Ex分量与Hy分量偶合、Ey分量与Hx分量偶合的关系相吻合；2个垂直场Ez分量与Hz分量则表现为半空间分布特征。Hx分量和Ey分量呈完全对称的4象限花瓣状分布，2条零值线通过正方形的中位线；而Ex分量和Hy分量的零值线交叉角并不是直角，且不经过正方形区域的对角线，存在场值范围较大的法向区域和较小的轴向区域，范围较大的区域也是传统电磁法(如CSAMT等)野外测量的布极区域。

图9 和图10 显示：在柱坐标与球坐标系下，所有分量的空间分布形态均表现为半平面分布状态，形似扇贝状，零值线或与天线方向平行，或与天线垂直。很明显，柱坐标系中的垂直场分量Ez、Hz与直角坐标中的Ez、Hz分量相同；球坐标系中的Eφ、Hφ分量与柱坐标系中的Eθ、Hθ分量相同。由于地球半径很大，因此，在以发射源为圆心、半径100km的范围内，球坐标系中的Er、Hr分量与直角坐标和柱坐标中的Ez、Hz分量是相等的。

2.5 波导区电磁波的空间分布特征

以θ和φ展开计算波导区场空间的辐射花样图，结果如图11 所示。从图中可明显看出，电磁场在90°和270°出现零值线，即过天线中点且与天线垂直的圆周线上的电磁场均为零值；在地球两极电磁场明显增强，表现出波的干涉增强特征，其余空间电磁场近似均匀分布，衰减很小。

图11 电离层-大气层-地球谐振腔模型的波导区CSELF电磁场空间分布图Fig.11 Spatial distribution of CSELF EM field in waveguide zone of earth-air-ionosphere model.

3 结束语

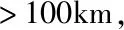
本文还给出了3种坐标系下近区、远区电磁波在空间的分布特征，发现场的空间分布中均存在场强为0的直线区域——零值线，零值线一般分布在天线的延长线或中垂线上，此外在直角坐标系下还存在2条斜交的零值线。布设野外观测台站时应尽量避免零值线的位置，若实际工作中不能避免零值线的方位，则可以选择在不同坐标系下进行理论计算，以化解这一问题。本文的这一研究结果对于人工源极低频监测台站的分布和数据分析具有指导意义。

通过对近区和远区近似解计算公式的分析，发现在基于水平电偶极子的频率域电磁测深方法中，近区电场的水平分量正比于介质的电阻率，而与频率无关，垂直分量与频率成正比而与介质的电阻率无关；磁场各分量的强度均与频率和介质的电导率无关；而远区电场水平分量基本与频率无关，对于测深没有直接贡献，远区电场的垂直分量虽然与频率和大地电导率均有关系，但由于观测困难，在实际测深中一般不使用，而相应的远区磁场的3个分量均与频率和大地电导率相关，故远区测深主要依赖于磁场而非电场。

由于CSELF天线一般很长(几十至上百千米)，在近区和远区进行测量时，天线已不能视为电偶极子，而应该视为由多个电偶极子构成的有限长导线源。本文依然采用电偶极子理论进行分析，具有一定的局限性，未来需要进一步深入研究加以克服。

致谢审稿专家提出的宝贵意见对文章的完善起到了重要作用，作者据此修正了相关计算公式，使计算结果更为客观准确，在此表示衷心感谢！