HVDC入地电流对地电场的影响规律及入地极定位

2022-08-04钱银苹

地震地质 2022年3期

章鑫范晔叶青钱银苹

1)广东省地震局，广州 510070

2)中国地震台网中心，北京 100036

0 引言

在固定地电场和地磁场观测中，常叠加人工源强电流的干扰，使得台站数据出现不同程度的脉冲扰动、台阶变化、基准值升高等现象。其中，高压直流输电(HVDC)的入地电流在固定电磁场观测中造成的扰动比较典型，换流站的入地电流在地电场中形成方波叠加(方炜等，2012；唐波等，2013；马钦忠等，2014)，其单极运行时导线中的强电流在地磁观测中形成强感应磁场，会在地磁观测中产生类似的方波叠加(方炜等，2012；蒋延林等，2014)。此外，城市轨道交通的漏电也是类似的固定点电流源干扰(邱颖等，2009；张宇等，2016)，与空间平面源的区别较大(刘连光等，2016；葛小宁等，2017)。这类扰动几乎固定出现，在长期的数据分析基础上易于识别，但其扰动程度在不同的台站具有较大的差异性。显然，这种差异性取决于源电流到观测点的传播过程，尤其是对地电场的叠加，地球表面的断裂带、山脉、海洋效应等都会影响台站的响应情况(魏敏敏等，2012；耿山等，2019)。那么，如果地震震源附近激发了地下自然电流，台站对这种未知源的响应必然也具有差异性，即地震电信号的传播通道也具有选择性(Sarlisetal.，1999；黄清华等，2010；马钦忠等，2014)，传播路径差异导致有的更远的台站能够响应某些信号，一些更近的台站则不能。研究电流传播路径差异造成的台站响应差异，是识别和定位震源激发电流信号的关键之一，HVDC向地下注入大电流是很好的研究范例。

电力部门已对存在入地大电流情形下的地表电位分布开展了较为详细的研究，包括一些特殊情形下的电位差异性分布。刘曲等(2007)研究了复合土壤模型下HVDC系统单极大地运行时的电流分布，在考虑海洋影响的情形下，利用土壤水平分层和垂直分层后的格林函数，通过镜像法推导出在复合分层土壤结构中地表电位的解析公式。为模拟多层介质并避免多重镜像下的复杂计算，当前业内主流的方法为行波法，其主要思想是将接地极电流在土壤中传播的过程类比为波在介质中的传播过程。任志超(2012)对基于各种模型的行波法、镜像法进行了详细推导，发现在垂向分层上各层存在的电阻率差异导致电流密度在界面处重新分配，即等效为波在不均匀介质间的传播，故存在波的反射和折射。一些学者进一步将行波法与镜像法相结合，推导出在海岸模型、断裂带模型等特殊情形下的解析方程，并将其用于估计变压器直流偏磁效应、计算换流站入地极附近的跨步电压(李泓志，2010；耿山等，2019；郭名文等，2019)。此类研究均只考虑入地极附近的几十千米内的情形，未考虑在入地极外几百千米范围的响应，同时也未考虑在地下十几千米左右的电流向地表传播时的响应差异，从而不能直接应用于地震监测预报工作中。

HVDC的入地电流是地电场观测中最显著的干扰源，在换流站附近几百千米范围内的地电场观测中均可引起较大阶变(方炜等，2012；马钦忠等，2014，2017)。在地电场日常观测中，对HVDC干扰源的识别通常来源于地磁数据的判别，一般不是通过地电场的响应直接识别干扰的来源方位。此外，向地下注入大电流时，可能造成较大区域内地电场台站的差异化响应，因此其成为研究电流到达台站通路过程的理想源。本文基于2个方面的目标开展研究：1)基于地电场矢量观测结果对高压直流换流站进行定位，依靠多个地电场台站的高压直流响应数据直接判别干扰来源；2)开展地电流到达台站的选择性通路研究，这种电性差异导致的差异性传播模型可推广应用到对地震电信号的识别。

图1 高压直流线附近的台站分布和构造要素Fig.1 Distribution of stations and faults near HVDC lines.The red triangle represents the disturbed stations，and the blue ones represent other stations in the area.a ±800kV海驻线的台站分布；b 宝德线入地极的位置和台站分布；c 扎青线入地极的位置和台站分布。红色三角为被干扰台站，蓝色为区域内其他台站，黑色箭头表示输电端和受电端的方向

1 高压直流干扰数据

1.1 高压直流干扰的数据

HVDC干扰的原因是以双线高压直流方式输电时，其中一条线路发生故障，另一条线路以大地作为回路的单极运行模式(李泓志，2010)，此时会在送电端换流站的入地极形成很大的入地电流，在受电端的入地极形成极性相反的入地电流。本文约定排名在前的换流站为送电端，排名在后的换流站为受电端(图1)，如扎青线的扎鲁特极为送电端、青州极为受电端。

本文以海驻线(海南藏族自治州—驻马店)、宝德线(宝鸡—德阳)和扎青线(扎鲁特—青州)为例(图1)，选取研究区域内沿线分布的58个地电场台站的数据进行分析，台站信息见表1；另外还使用山东大山台极低频数据作为响应差异的对比。海驻线两侧的地电场台站分布相对均匀，入地极两端也有较多的地电场台站分布，涉及29个台站；宝德线受影响的台站较少(7个)，影响范围小；扎青线两侧的台站基本都分布在换流站一侧，极度不均匀，但影响的空间范围大，涉及22个台站。

表1 台站信息及阶变量计算结果Table 1 Station information and partial results of step changes

地电场的仪器响应频率为DC-0.01Hz，采样频次为1min，每天产出1440个数据。这些台站均采用 “多方向、多极距”的地电场观测方法(席继楼，2019；章鑫等，2020)。本文约定EX、EY和NE分别表示长极距的NS向、EW向和NE向(斜道)分量，ex、ey和ne分别表示短极距的NS向、EW向和NE向(斜道)分量。大山台为地电场和极低频同台观测，极低频仪器的观测频段为3.9～0.001Hz，采样率为16Hz，2个正交通道(LEX、LEY)同时观测，本文使用2020年4月23日的数据。

高压直流对地电场的干扰本质上是换流站不平衡入地电流的加载，单极运行时不平衡电流的峰值为额定电流的1.5倍(李泓志，2010)，且持续时间达到几十分钟。这种干扰的幅度在换流站附近最大，电流影响周围约500km范围内的地电场观测。但这是一种差异化的影响，如在海驻线受干扰的台站中，离两侧入地极最近的都兰台和嘉山台尤为显著，其他远端台站的阶变量较小。具体干扰的数值参见表1。

高压直流入地电流对地电场有3种加载方式，并形成3类响应，分别为台阶状阶变、脉冲状响应及脉冲+半台阶状响应。其形成的原因分别为：

(1)靠近入地极的地电场台站受到单个入地极电流的影响，地电场2个电极附近的电位被抬高，与大地电流形成的原始日变化曲线相比，出现了上升或下降台阶(具体为上升还是下降取决于观测方位与入地极的相对方位和入地极的极性)；当入地极无大电流注入时，观测电位将恢复到原始日变化形态，此时形成了下降或上升台阶，与注入电流时的台阶反向(图2b)。

图2 不同位置的台站受到海驻线影响的结果Fig.2 Results of different stations that are affected by Hainanzhou-Zhumadian line.a 代表性响应台站及其位置示意图；b—d 都兰台、凤翔台和大山台受影响的观测曲线；图b为第1类响应，只受到一侧极的影响；图c为第2类响应，同时受到两侧极的影响且影响几乎相当；图d为第3类响应，受到两侧极的影响且以一侧极为主。干扰发生的时间为2020年7月11日和2020年4月23日

(2)处于2个入地极中间位置的台站受到2个入地极电流的共同影响，一个入地极的电位使地电场的正常曲线上升，而另一个入地极的电流极性相反，会使其电位下降、地电场曲线小幅下降，形成脉冲型响应。此外，2个入地电流引起的场是同时形成的，故在中间区域的台站电位上应表现为互相抵消。但该响应是入地电流的一阶微分、入地极的系统响应和地电场观测装置传递函数三者的卷积，故地电场电极对电位的响应存在延迟，先响应一个入地极的电位(上升或下降)，再响应另一个入地极(下降或上升)，由此形成了脉冲型响应(图2c)。

(3)处于2个入地极的中间地带但离其中一个入地极偏近的台站，将受到一个入地极的主要影响和另一个入地极的次要影响，因此近处的入地极使其出现台阶，远处的入地极使其部分台阶恢复、形成脉冲，其结果即为台阶+脉冲的形态。同时应注意到，图2b 中都兰台的台阶起始时间为1011分，而菏泽台的台阶起始时间为1013分，即受电端的响应延迟了2min，这就证实了脉冲型响应或台阶+脉冲响应由2个入地极分别作用所引起，且送电端(都兰台)先出现响应。

大山台的脉冲+台阶响应较为典型，我们获取了同时段的极低频观测数据作为对比。图3a、b为地电场观测的数据，可见2020年5月23日大山台受到2条高压直流输电线路的干扰，台阶之间相互叠加，扎青线的干扰先行结束；还需注意到，另外一条线路的干扰仅为台阶状，说明大山台只受到其中1个入地极的影响。图3c 为极低频数据的响应情况，LEX在3～4h段有1个缓变台阶与图3a 中同时段的台阶+脉冲对应，但在该台阶的恢复阶段(6～7h)LEX无明显扰动；在23h附近地电场EX分量有明显的向上阶变现象，在同时段LEX有明显的向下波动与之对应。此外，LEY全时段无明显响应，同时图3b 中地电场分量EY对高压直流的响应也较弱，说明这2条高压直流干扰都主要影响地电场分量EX和极低频分量LEX。图3d 和图3f 为D1、D2时段的放大图，图3e 和图3g 为E时段的放大图，可以看出极低频观测具有与地电场对应的高压直流干扰响应，与换流站连线垂直的LEX分量更为强烈，与换流站位置连线平行的LEY分量更弱。

图3 大山台地电场观测数据与极低频观测数据对高压直流的响应比较Fig.3 Comparison of the responses of geoelectric field data and extremely low frequency data to HVDC at Dashan station.a 地电场EX分量；b 地电场EY分量；c大山台极低频电场的观测值；d、f D1、D2时段的放大图；e、g E时段的放大图。LEX表示极低频电场的EX分量，LEY表示极低频电场的EY分量；图3d—g 表示截取典型响应的台阶(或脉冲)时段。D1和D2 表示2个独立的干扰阶段，E表示扰动时段同时存在于地电场观测与极低频观测中

1.2 阶变量的校正

为改善直接采用原始曲线计算分幅度值造成较大差别的不足，我们采用同台站、同方向的正常日变化量对阶变幅度进行校正。首先，计算入地电流引起的阶变量S：

S=max(E(i))-min(E(i))

(1)

其中，S表示阶变的幅度，E(i)为原始时间序列；i为阶变发生的时段，i的取值为扰动阶变的起始到终止。

其次，计算扰动发生前、后2d中1d正常的日变量，选取曲线比较光滑的日变曲线计算日变化幅度。计算前先对日变曲线进行滤波，采用40阶FIR低通滤波器，通带截止频率为0.001Hz：

D=max(E(j))-min(E(j))

(2)

其中，D为日变幅度，E(j)为原始时间序列，j为正常日变化的时段，取值为1～1440min。最后取两者的比值R：

R=S/D

(3)

计算出两者比值后，即完成对原始阶变幅度的日变放缩校正。该方法的关键在于2个方面：1)求出准确的阶变，一些台站的阶变量很小，从而容易受到其他因素的影响，而准确量取入地电流影响的阶变量是比较困难的；2)选取正常的日变曲线，由于地电场观测对环境电磁干扰非常敏感，从4d的数据中选取相对光滑的1d的日变曲线也比较困难。

2 地电场对高压直流的响应特点

单个高压直流入地极加载时，阶变量由近到远逐渐减小。从台站与驻马店换流站的距离来看，图4a 中EW向阶变量SEX随距离的增加逐渐递减。但SEX的大小还取决于台站所在换流站的方位，观测方位接近于入地极径向方位上的电位差必然大于其他方位，因此单一近NS向的观测结果并不能真实地反映距离的影响。此外，SEX的响应时间有延迟，一些台站的延迟可达3min(图4b，c)，这可能有2个方面的原因：1)该响应是入地电流的一阶微分、入地极系统的响应和地电场观测装置的传递函数三者的卷积；2)地电场仪器本身存在钟差的影响。

图4 按照距离排列的驻马店入地极附近台站EX分量的阶变情况(a)及阶变延迟信息(b、c)Fig.4 The EX order variables that are arranged by distance of stations near the Zhumadian ground electrode(a)and step delay information(b，c).

由于阶变量与台站到入地极的距离有关，我们计算了受影响台站的阶变幅度或脉冲幅度，同时还考虑不受高压直流影响下的日变化幅度。图5 和图6 中的阶变量比是2个正交方位幅度比合成后的幅度RC，计算方式为

(4)

式中，REX和REY分别为2个分量的阶变幅度。此外，合成阶变量SC的计算方式为

(5)

其中REX和REY分别为2个分量的阶变幅度。图6 为海南藏族自治州入地极的合成阶变量，并按照与换流站的距离进行排列。从图5a 中可以看出，阶变的影响范围约达580km，原始阶变幅度SC随距离的变化并不明显，日变化幅度D也没有明显的规律。但在求取与日变化幅度的比值RC后(图5b)，结果显示RC与台站所处的位置明显相关，即RC具有随距离(与换流站的距离)递减的变化规律，且基本符合一元二次函数的衰减趋势(图5b 中的黑色曲线)。此外，一些台站的观测场地受到的干扰比较复杂，根据滤波后求出的S和D都存在一些误差，导致RC的衰减关系与拟合曲线有一定的偏差。

图5 驻马店入地极附近台站的阶变量、日变化幅度(a)及两者比值(b)Fig.5 The step changes，daily variation range，and their ratio of stations near the Zhumadian grounding electrode.

图6 为海南藏族自治州入地极的阶变幅度情况，距离入地极较近的台站较少。天祝台阵与入地极的距离基本相当，且与入地极的方位相差不大，但其SC却差异较大，且D和S都相差较大(表1，图6a 中的300km处)。与图5b 相比，图6b 中的递减趋势更为明显，但响应范围较小，影响距离最远约为500km。处于单个入地极影响范围外的合阳、凤翔等台站受到了2个入地极的共同影响，其响应为脉冲状或台阶+脉冲状，且SC不满足递减规律。

图6 海南藏族自治州入地极附近台站的阶变量、日变化幅度(a)及两者比值(b)Fig.6 The step changes，daily variation range，and their ratio of stations near the Hainanzhou grounding electrode.

3 利用方向和幅度开展入地极定位的结果

3.1 定位原理

在均匀各向同性的电性条件下，电位分布是由入地点向外围均匀扩散的。那么在观测点处的电位差取决于大圆路径的径向分量在2个正交方位的投影。因此，在观测正确的情况下SEX和SEY有明显差异，可以通过2个正交方位的电位差合成矢量SCP(表示具有指向性的阶变量合成值)，该矢量即指向入地极的位置，如图7a、b中南京台。根据将2个正交方位阶变量合成的矢量SCP具有指向电流源位置的性质，可基于单个台站的数据对电流源进行定向。在1个入地极附近有多个台站的观测数据产生阶变时，通过多台SCP的反向交会，能够初步定位入地极的位置(图7c)。

图7 高压直流的电位方向性响应及电位方向差异定位原理Fig.7 Potential directional response of HVDC and the principle of locating by potential direction difference of HVDC.a 南京台短极距对三常线(三峡—常州，年5月9日的阶变；b 南京台短极距阶变的方向性响应；c 基于2个虚拟台站的电位方向差异的定位原理示意图

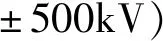
3.2 阶变比值矢量方向定位

海驻线两端位于青海海南藏族自治州共和县(龙羊峡附近)和河南省驻马店市上蔡县。我们采用了阶变与日变幅度比值的方法对海驻线2个入地极的位置进行定位，即先计算有入地电流时的阶变量，再取其与正常日变化量的比值。图8 是采用矢量归一化(对矢量模的大小进行归一化，把所有矢量的长度都归算为归一化定位的结果，阶变比值合成的矢量对于入地极的指向性更明显。在入地电流的注入阶段，海南藏族自治州入地极的阶变比矢量都远离入地极的位置；在恢复阶段，海南藏族自治州入地极阶变比矢量指向入地极的位置。而在驻马店入地极附近，阶变比矢量的方向与海南藏族自治州入地极相反，即注入阶段指向入地极，恢复阶段远离入地极。此外，处于2个入地极中段位置的几个台站(虚线椭圆内)的SCP无明显指向性，但倾向于垂直2个入地极的连线。

图8 海驻线阶变比的矢量归一化定位结果Fig.8 The locating result of Hainanzhou-Zhumadian line by using composite vector of step changes.

图9 阶变量合成矢量归一化的方向Fig.9 Direction of composite vector of step changes.a 扎青线入地极的定位结果；b 宝德线入地极的定位结果

对于扎青线2个入地极(图9a)，扎鲁特入地极附近的台站都分布在东侧，青州入地极的台站几乎分布在西侧。使用扎青线这种台站严重分布不均匀的线路进行定位且得到了较好的结果，说明一般性的高压直流入地极也能被定位。一端的SCP在电流注入开始阶段远离入地极，在电流恢复阶段指向入地极；另一端则相反。在图9a 中，扎鲁特东侧的SCP基本都指向扎鲁特入地极，扎鲁特南侧的2个台站(阜新台和锦州台)的SCP也指向北侧的入地极；在青州换流站西北侧的地电场台站中，其SCP也几乎指向青州入地极所在的位置。与海驻线相似，在2个入地极之间的昌黎台SCP指向不明显，倾向于垂直于2个入地极的连线。

宝德线是500kV的高压直流输电线，建成于2009年，前人对该线路的干扰研究较多(方炜等，2012)。这条线路的额定电流为3000A，单极运行时向地下注入的电流较小，影响范围较小，在本文所选的例子中仅影响了7个台站。基于这些台站的阶变数据对入地极的定位结果与前述2条线路类似，北侧宝鸡入地极附近的台站密集、响应明显，对其入地极位置的定位比较明确；南侧德阳附近仅有成都台和江油台，对德阳入地极的定位效果不理想。当台站周边无多个换流站时，也能依靠SCP粗略定位判断所属的干扰源。

3.3 矢量幅度定位

高压直流引起的阶变，其变化量的幅度信息也可被用于对入地极的定位中。在表1 中，我们可以通过观测台站的阶变量初步判断入地极距离某个台站最近，如海驻线的大武台和周口台、宝德线的宝鸡台、扎青线的阜新台等。但一些台站并非位于入地极附近，其阶变量却是最大的，如海驻线中的应城台，通过这些台站还不能准确判断入地极的位置。另外，虽然SCP矢量的方向可指示换流站位置，但由于距入地极较近的台站较少，而远处台站的SCP难以在一个很小的范围内交会，从而影响了定位的准确性。为此，我们使用经过日变化幅度校正的RC作为定位的补充。图10 为海驻线的RC在平面上的投影。在入地电流开始注入和恢复双极运行时，入地极附近的RC均为最大，能够在入地极被台站包围较好的情况下指示入地极的位置。此处的RC经过了日变化幅度校正，故单独使用幅度信息时，可以认为RC出现极大值的位置即为最靠近换流站位置；远离换流站时则幅度变小。因此，若台站足够密集，并正确地获取幅度信息时，其定位的结果也能够反映入地极的位置。

图10 阶变比值的强度排序Fig.10 Intensity rank of step change and diurnal variation ratio of Hainanzhou-Zhumadian line.a 海驻线电流开始注入阶段；b 海驻线电流恢复阶段

4 讨论

前人的研究多只关注一个入地极的影响，而电力部门一般只关注单个入地极引起的跨步电压，不关心2个入地极共同作用下的脉冲型响应。在2个入地极间的台站受到了2个入地极的共同影响，其响应特点具有特殊性(图11)。与台阶响应不同，受到一个台站向上阶变、另一个台站向下阶变的叠加，2个换流站之间的地电场响应多以脉冲形式出现。距其中一个入地极近时，其脉冲受到该入地极的影响较大、另一个入地极的影响较小，可能会出现脉冲+台阶的形式。且正交观测的脉冲合成矢量不一定指向入地极位置，因此根据2个换流站之间的台站很难准确定位入地极。这是由于阶变量之间相互叠加而无法准确量取每个入地极的影响，且脉冲式的响应不能准确反映电位差异。

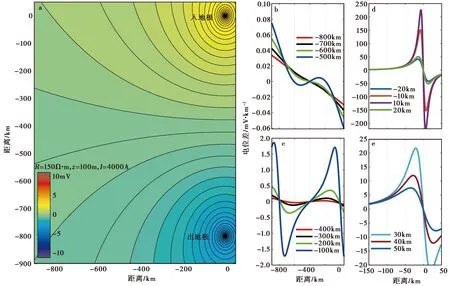
图11 理想导电状况下的电位分布及电位差衰减Fig.11 Potential distribution and difference attenuation under ideal conduction condition. a 2个入地极附近的电位取对数(log10)的分布，单位为mV；b、c 对图a中沿y轴求电位差的结果，在范围每隔100km取1条线，单位为mV/km；d、e 对图a中沿y轴求电位差的结果，在范围每隔10km取1条线，除通原点的线，单位为mV/km。入地电流强度为4000A，电阻率为150Ω·m，埋深100m

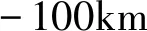
根据图11 中入地点电流源引起的电位分布情况发现，文中得到电位差的影响范围与理论值相差较大。如海驻线的大山台与驻马店入地极的距离超过550km，扎青线的德都台与扎鲁特入地极的距离超过650km，均远超模型给出的200km影响范围。此外，重庆仙女山台的响应距离接近750km，马钦忠等(2017)和赵文舟等(2022)的研究也显示仙女山台对其他线路的换流站有远场响应，这或许说明存在某些 “敏感点”台站，对入地电流的响应距离非常远，且这种现象在东部平原区域比较明显。西部宝德线的2个入地极和海南藏族自治州入地极的影响范围都比较有限，除了处于2个入地极之间的台站外，海南藏族自治州入地极与其北部最远的武威台相距约300km。郭名文等(2019)加入断裂模型后的模拟结果表明，距离超过30km后断裂对电位的分布响应很小，地电场台站几乎都处于入地极30km外，但从地电场观测结果来看其影响并不小。由此可见，现存的入地电流引起的电位差模型还需要进行较大改进，如存在某些低阻的电流通道，将使入地电流经过通道形成新的电位源，从而影响到较远的台站。

此外，本文的定位方法还存在一些局限性，主要体现在观测的准确性和台站分布2个方面。受到观测中其他干扰(如地铁运营)或观测系统(如极性接反)的影响，计算入地电流引起的阶变时存在误差，影响了最终合成矢量方向的准确性。此外，一些台站的位置特殊(如沿电流通道分布)，可能存在不均匀电流源现象，即电位差的梯度方位不是入地极方位，而地电场观测阶变反映的是电位的梯度方向，这一差异影响了定位的准确性。

同时，台站分布的影响也较大，主要受限于入地极周围的台站数量和分布是否环绕入地极。理想情况下，台站越密集且越靠近入地极，反映的入地电流电位分布特征越准确，也就能够更准确地定位源的位置，反之则很难准确定位。即在台站数量多且分布基本环绕入地极的情况下定位效果较好，反之则较差。在本文的例子中，海驻线西侧海南藏族自治州入地极的台站基本分布在其周围，定位效果较好；扎青线扎鲁特极附近的台站基本分布在入地极东南一侧，其SCP的指向基本正确，但比海驻线的效果稍差；宝德线的宝鸡入地极附近台站分布相对均匀且环绕入地极，定位效果较好，而德阳入地极附近台站少，其SCP未能准确反映入地极的位置。

研究入地电流对地面地电场、地磁场的影响，可进一步推广到对地震电磁场响应的探索中。地震电磁场观测台站通常布设在断裂带附近，依靠这些台站的观测数据，能够对一定条件下强震的发生做出趋势性预测，并给出地震发生的空间范围和时间窗口。但对震源附近电磁场信号如何传播到观测台站的解释还不很令人满意，时常一些较远的台站有异常、而就近的台站无异常，即差异化响应比较明显。且这种预测一般难以做到临震预测，即异常信号可能来自于震源区，但不一定是由该次地震活动所激发，这就需要考量这种震源区的信号是如何传播到台站的，为何造成了差异化响应等问题。当然，典型的同震电磁信号被认为是由地震波所激发，且已被理论推导和一些实际观测所证实(Gaoetal.，2014；Renetal.，2018)，但其信号的主要频带在固定地电、地磁观测的主要频带之外。固定地电场台站能够识别的是直流—准直流信号，地磁台站主要观测震源激发电流的感应磁场，研究入地电流信号的传播特点有助于从观测数据中识别与震源过程有关的电磁现象。此外，本文对入地电流在地电场观测中的响应研究表明，仅依靠多极距多方位共同响应来判断 “远源”信号这一方法具有较大的局限性，还需要考量响应的方向性、传播通道等因素。