基于全体圈个数为4的LFSR 构造de Bruijn 序列的研究

周琮伟，胡斌，关杰

（信息工程大学密码工程学院，河南 郑州 450001）

0 引言

近几十年来，线性反馈移位寄存器（LFSR,linear feedback shift register）序列被广泛应用于通信编码和密码算法中，例如众所周知的m序列。然而由于LFSR固有的线性制约性及输入的多条乱源序列存在时间差，可以对其经过非线性改造产生的密钥流的序列周期与线性复杂度进行深刻的代数刻画[1]，并且在此基础上提出的相关攻击[2]、最佳仿射线性攻击[3]与代数攻击[4]等分析方法均有对应的算法攻击实例，因此逐渐将研究对象从LFSR 转向非线性反馈移位寄存器序列。其中n级de Bruijn 序列是一类重要的非线性反馈移位寄存器序列，其圈结构中圈长达到最大周期2n，同时其伪随机性质与线性复杂度[5]均优于m序列。此外，de Bruijn 序列在卫星通信[6]、电网技术[7]和基因测序[8]中均有广泛应用。

构造de Bruijn序列一直以来都是研究de Bruijn序列的核心问题，其构造思路主要是基于反馈移位寄存器圈结构中各圈的合并，其难点在于研究各圈上的共轭状态分布。在20 世纪70 年代至90 年代，国际上掀起了研究构造de Bruijn 序列的热潮，各种算法和结果层出不穷[9-17]，其中文献[12]比较全面地介绍了de Bruijn 序列构造的经典算法。近期国内学者也给出了一些构造算法[18-19]，但快速构造密码学性质良好和实用性强的de Bruijn 序列特征函数仍然是一个长期亟待解决的问题。

从20 世纪70 年代起，Lempel[20]引入D-同态的概念，利用n级de Bruijn 序列在D-同态下的原像是2 个n+1级的等长圈，并结合2 个等长圈上共轭状态的分布特点，给出了一个由n级到n+1级de Bruijn 序列特征函数的递归构造方法，且可以进一步拓展到n+2级[21]。此类递归思路实际上可以看作产生n级de Bruijn 序列的非线性反馈移位寄存器级联小级数的LFSR，Chang 等[22]利用线性方程的方法给出了较为清晰的代数表达式。

另一方面，Li 等[23-25]、Li 等[26-27]和Chang 等[28]研究了几类级联型LFSR的特征多项式，给出了其中几个n级LFSR 圈结构的因子关联图，从而给出了其构造的算法和计数。特别地，Dong 等[29]还研究了利用仿射反馈移位寄存器构造de Bruijn 序列的方法。以上方法均建立在小级数的LFSR 级联特征多项式为本原多项式的LFSR。同时，Dong 等[30-31]还研究了周期为的n次不可约多项式为特征多项式的LFSR 圈结构的因子关联图，证明了其特征多项式的邻接矩阵（因子关联图的矩阵化）与本原多项式的k−邻接矩阵相等，并利用雅可比和给出了k=3,5时其对应的k−邻接矩阵元素的具体表达式，即从理论上给出了这类de Bruijn 序列的计数。从构造的实用性角度上分析，通过并圈方式直接构造的de Bruijn 序列特征函数基于的LFSR 圈结构中圈个数越少，效率一般越高。由于LFSR 圈结构中圈个数一定为偶数[17]，且等于2的情形为m序列中添加一个零，因此本文进一步研究基于圈个数为4的LFSR 构造de Bruijn 序列的方法。同时，为了拓宽上述研究所基于的LFSR 种类，增加构造的de Bruijn 序列数目，给出更多清晰的de Bruijn 序列特征函数形式，本文的工作延续和拓展了上述文献中的构造方法，并结合文献[31]的相关结论，提出了基于全体圈个数为4的LFSR 构造de Bruijn 序列的方法。

1 一类级联型的反馈移位寄存器的圈结构

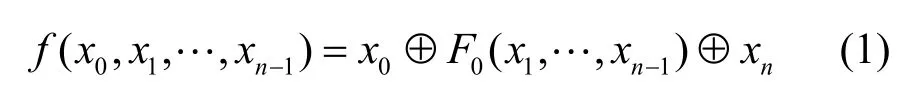
由于非奇异反馈移位寄存器产生的输出序列都是周期的，因此可以在此基础上定义序列的左移变换为

为Ω(f)的一个平移等价类或者一个圈。若Ω(f)有r个圈，则Ω(f)或反馈移位寄存器的圈结构可以写作

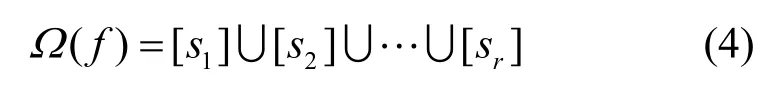
引理1 表述了圈结构中非常重要的圈合并与圈分解的概念。

引理1[32]设ν=(v0,v1,…,vn−1)在圈[si]上，其共轭状态=(v0⊕ 1,v1,…,vn−1)在圈[sj](j≠i)上，则可以通过交换ν和νˆ这2 个状态的后继使这2 个圈合并为一个圈，其对应的圈合并后的特征函数为

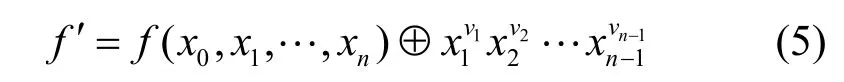
同理，若ν和其共轭状态都在圈[si]上，则可以通过交换ν和这2 个状态的后继使这一个圈分解为2 个圈，其对应的圈分解后的特征函数也如上。

级联或者称为反馈移位寄存器的串联始见于文献[33]，由定义1 描述。

定义1设n级的反馈移位寄存器在初态(a0,a1,…,an−1)下产生序列a且特征函数为f，m级的反馈移位寄存器初态为 (b0,b1,…,bm−1)且特征函数为g，则称特征函数为f∗g的反馈移位寄存器为级联型，其输出序列b满足

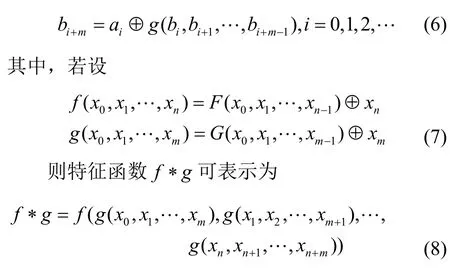
特征函数f∗g对应的m+n级的级联型反馈移位寄存器的结构框架如图1 所示。

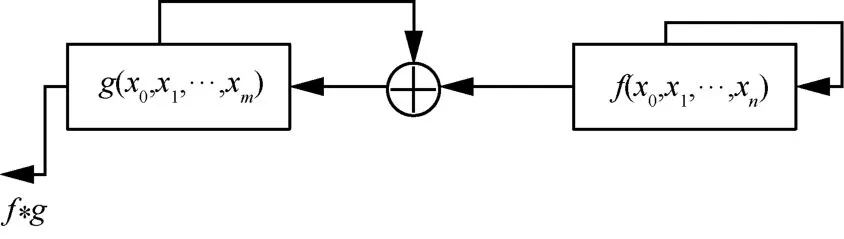
图1 特征函数f ∗ g对应的m +n级的级联型反馈移位寄存器的结构框架

为了研究基于LFSR的反馈移位寄存器的级联特征，本文首先给出LFSR 特征多项式的相关概念。设全体LFSR的特征函数形如

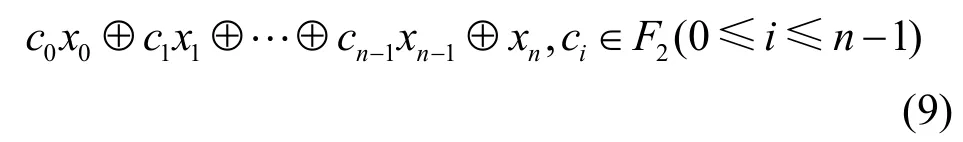
则存在F2上的一一映射

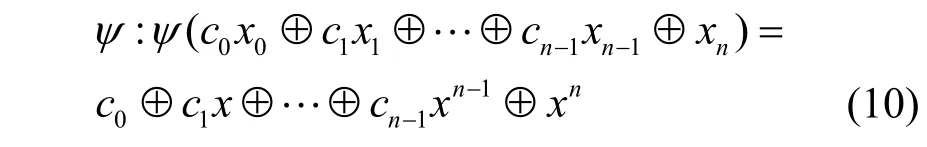
此时，称ψ(x)为该LFSR的特征多项式。文献[17]指出，若ψ(x)为F2上的n次不可约多项式，则该LFSR的圈结构Ω(ψ(x))可表示为

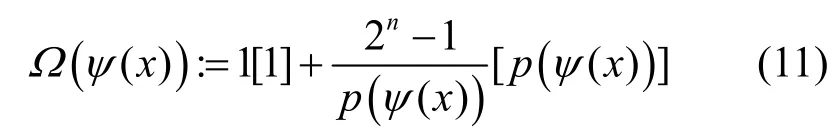
其中，• [ ∗]表示圈长为∗的圈有•个，p(ψ(x))表示ψ(x)在F2上的周期。因此，如果可以将F2上的任一特征多项式分解为若干不可约多项式的乘积[17]，则可以确定LFSR的圈结构。文献[34]证明了包含LFSR的一类级联型反馈移位寄存器的输出序列的周期分布情况，即引理2。

引理2[34]设g(x0,x1,…,xm)是LFSR的特征函数，其特征多项式ψ(g)为F2上的m次不可约多项式，且设

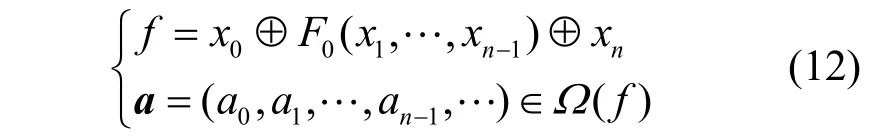
其中，序列a的周期表示为p(a)。

1) 若p(ψ(g))/|p(a)，设在初 态 (a0,a1,…,an−1)加载下，特征函数为f∗g的级联型的反馈移位寄存器生成的序列集合为θ(g)−1(a)，则θ(g)−1(a)包含一条周期长度为p(a)的序列和2m− 1条周期长度为 lcm {p(a),p(ψ(g))}的序列，其中lcm{p(a),p(ψ(g))}表示p(ψ(g)),p(a)的最小公倍数。

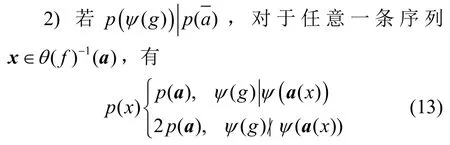
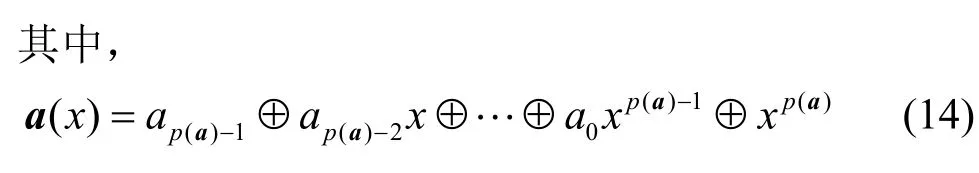
通常，基于级联型反馈移位寄存器构造de Bruijn序列的方法主要是将给定的特征函数依据引理2的1)中的限制条件代入级联型的递归式，并直接对集合θ(g)−1(a)中的生成序列按平移等价进行分类，便可推导出其圈结构中的圈个数，即定理1，从而进一步得到这类级联型反馈移位寄存器的圈结构Ω(f∗g)。

均与B′平移等价，且仅限于取它们作为初态时所得序列。注意到，B′的周期为q=Pp(a)，因此

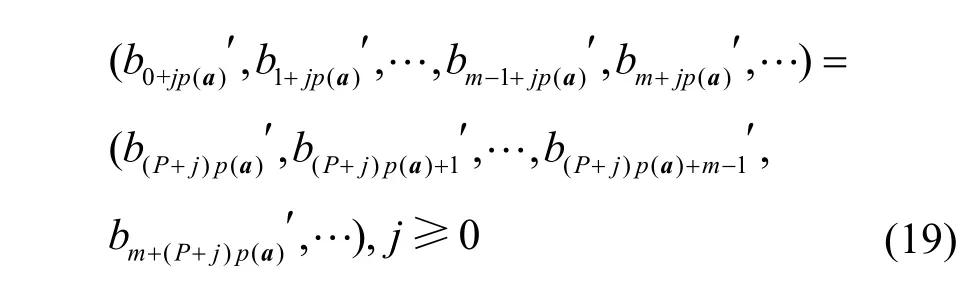
只有前P个两两不同的数组作为初值产生的序列与B′平移等价。根据上面的讨论，所有平移等价的序列在同一个圈上，因此共有

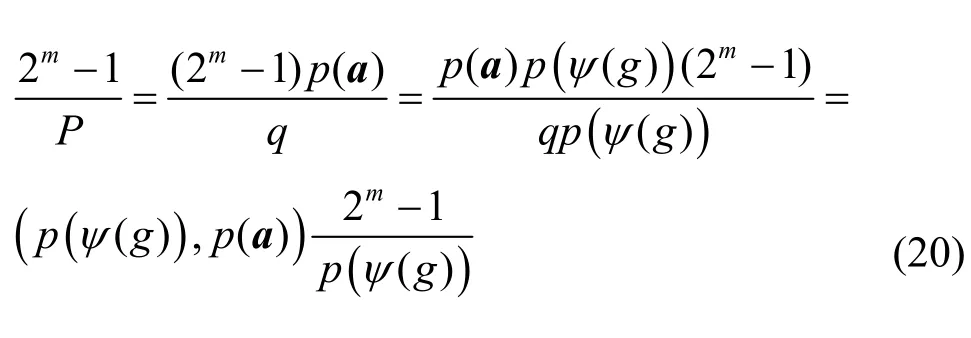
个周期为q的圈，加上一个周期为p(a)的圈。证毕。

若Ω(f)中的每个圈圈长都不被p(ψ(g))整除，将Ω(f)中所有平移不等价的序列代入定理1，可以立即推出这类级联型反馈移位寄存器的圈结构，即推论1。

推论1 设g(x0,x1,…,xm)是LFSR的特征函数，其特征多项式ψ(g)为F2上的m次不可约多项式，设

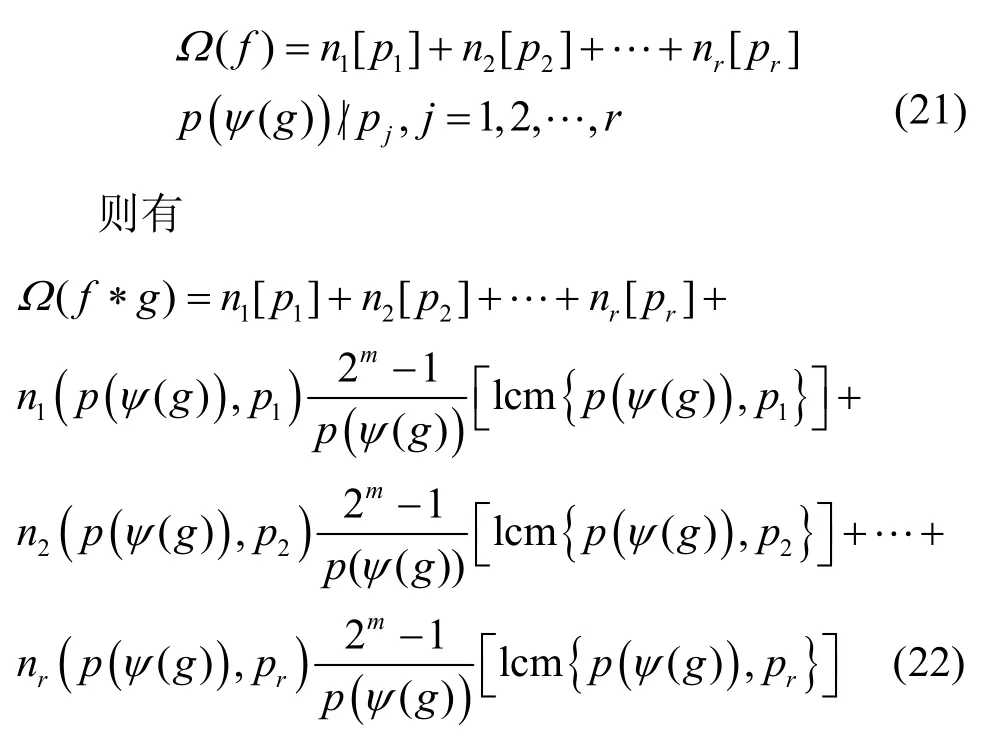
2 构造de Bruijn 序列的方法

利用f∗g的特征函数结构，可以给出任意n级LFSR 与级联型反馈移位寄存器之间的关系。

定理2任意n级LFSR 等价于唯一确定的若干LFSR 经过级联生成的级联型反馈移位寄存器。

证明设n级LFSR的特征函数为

代入式(29)可得h(x) ∗g(x) =f(x)，即特征函数为h(x)和g(x)对应的LFSR 级联生成的级联型反馈移位寄存器恰为特征函数为f(x)对应的LFSR。进一步地，对于ψ(f(x))分解为一般情况时，本文可以反复迭代上述过程，又根据多项式的唯一分解定理，因此任意LFSR 均等价于唯一确定的若干LFSR经过级联生成的级联型反馈移位寄存器，此时其特征多项式分解的若干不可约多项式恰为级联型反馈移位寄存器中各LFSR的特征多项式。证毕。

根据定理2 以及推论1，由于LFSR 圈结构中圈个数至少为2，则对于任意圈个数为4的n级LFSR 等价的级联型反馈移位寄存器，级联的LFSR个数最多为2，因此可得定理3。

定理3圈个数为4的n(n≥ 3)级LFSR 个数为

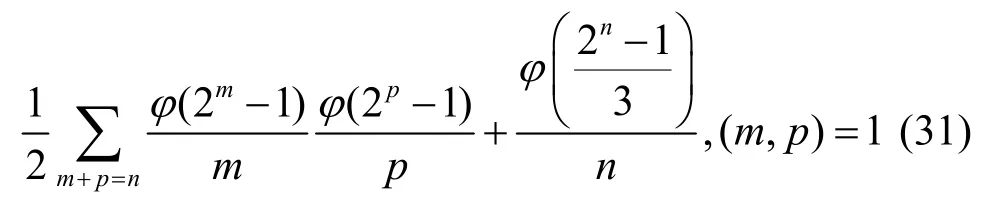
其中，φ为欧拉函数，当x不为整数时，φ(x)=0。

证明定理2 中，对于任意n级LFSR的特征函数

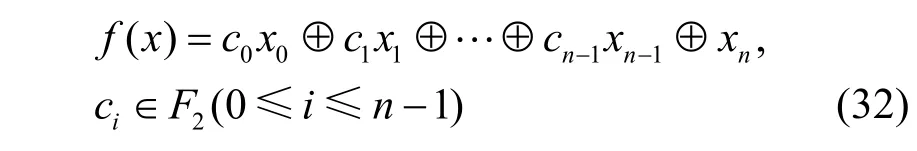
本文要求其为非奇异，即c0=1。当n=1时，ψ(f(x))只能取1⊕x，故其圈结构为

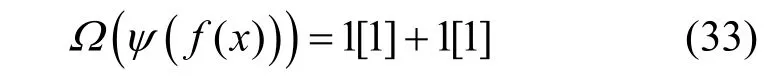
当n>1时，由于ψ(f(x))可以分解为若干不可约多项式的乘积，而这些不可约多项式恰好对应级联型反馈移位寄存器中各LFSR的特征多项式，当特征多项式为不可约多项式ψ(x)时，其圈结构可表示为

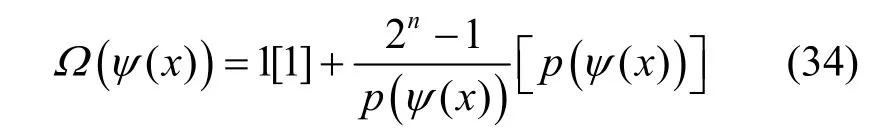
综上，当n为任意正整数时，其分解的不可约多项式对应的LFSR 圈结构中圈个数至少为2。根据推论1，若分解的不可约多项式超过2 个，则圈个数超过4，故分解的不可约多项式至多为2 个。

当ψ(f(x))为不可约多项式时，可得

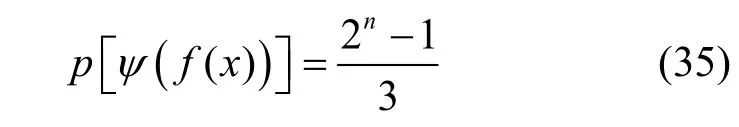
根据文献[35]，F2上周期为l的n次不可约多项式的个数为在此情形下，其圈个数为4的LFSR 个数为

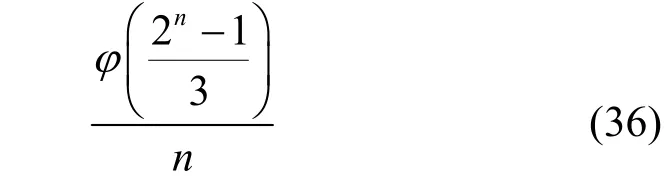
当ψ(f(x))分解为2 个不可约多项式的乘积时，分别设这2 个不可约多项式为

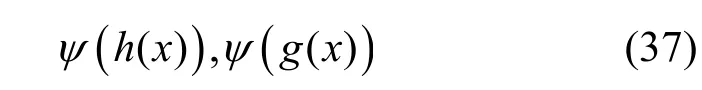
且满足ψ(f(x))=ψ(h(x))ψ(g(x))，其级数为m,p且m+p=n，根据推论1，不可约多项式对应的LFSR 圈结构中圈个数只能为2，故此时这2 个不可约多项式即本原多项式，又根据辗转相除法，当且仅当(m,p)=1时，有

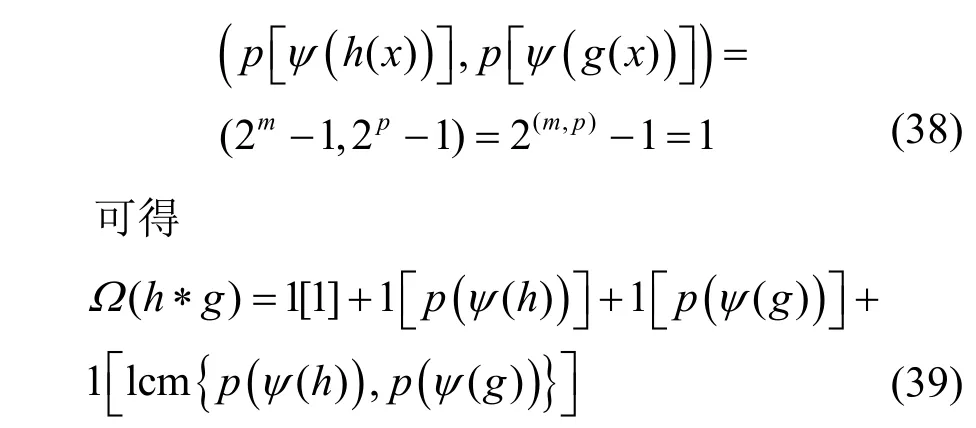
此时，圈个数恰为4。注意到，当h和g均为线性情形时，Ω(h∗g)=Ω(g∗h)，在此情形下，其圈个数为4的LFSR 个数为

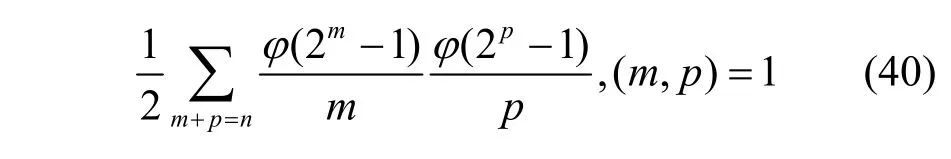
综上，本文要求n≥ 3是因为m和p不能同时为1，当n=3时，唯一一个圈个数为4的LFSR的特征函数为x0⊕x3。2 种情形的个数加之，定理3 即证。证毕。

文献[31]证明了定理3 中当ψ(f(x))为不可约多项式时，通过圈合并的方法可得到的de Bruijn 序列个数为

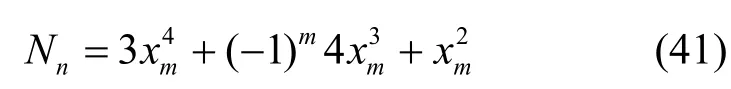
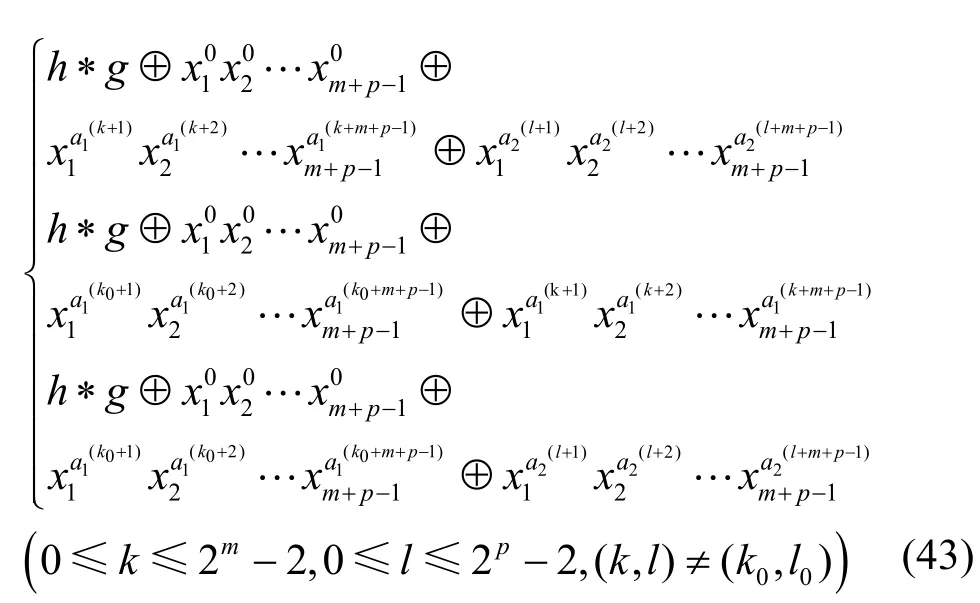
定理4设任意m级和p级LFSR的特征函数分别为的级联型反馈移位寄存器产生de Bruijn 序列。且产生周期为2m+p的de Bruijn 序列个数为

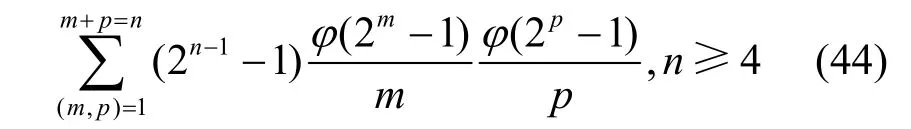
证明根据定理3 可知，当(m,p)=1时，Ω(h∗g)中的圈个数为 4，故可设对应的圈为{0,b1,b2,b1+b2}。由于a1,a2是m序列，故圈b1,b2上的状态均不可能是共轭的。下证圈b1,b2之间只有一对共轭状态，设 (x0,x1,…,xm+p−1)在b1上，(x0⊕ 1,x1,…,xm+p−1)在b2上，则满足

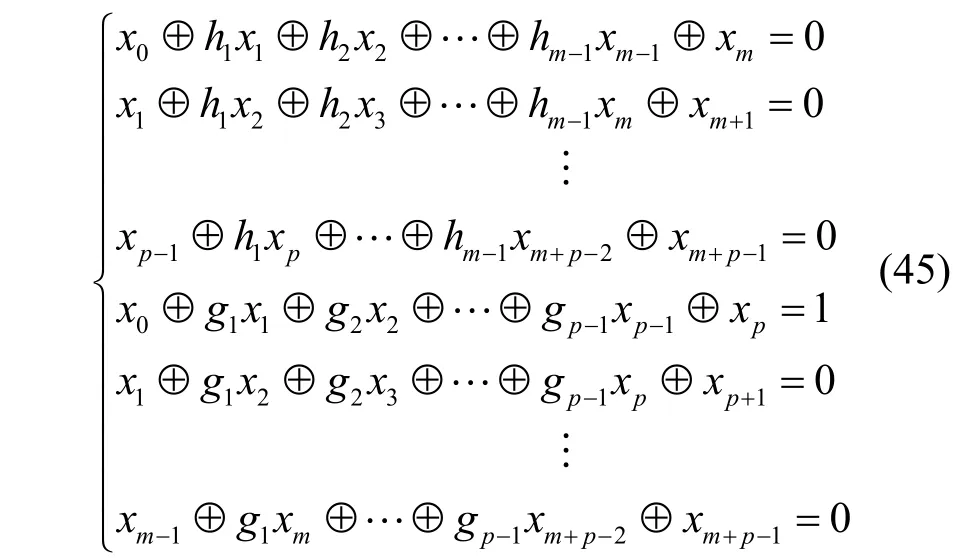
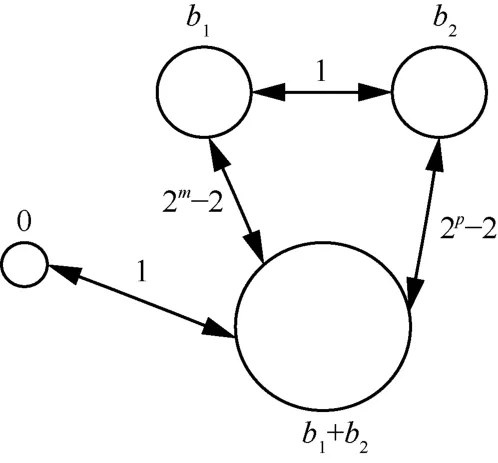
图2 4 个圈之间的共轭状态分布

使这4 个圈合并的方式共有2 种。

2) 先合并圈b1,b2，然后合并b1+b2，最后合并0。

这2 种方式产生de Bruijn 序列的特征函数分别为

接下来固定h,g，判定这2 种方式产生de Bruijn 序列的个数。

针对方式1)，本文假设存在一组(k′,l′)，满足则可得判定式

同理，针对方式2)，由于只有唯一的小项需要比较，故此方式产生的de Bruijn 序列个数为

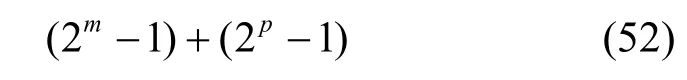
综上，固定h,g之后，这4 个圈合并产生de Bruijn 序列的个数为2m+p− 2。下证当h,g变化时，只针对方式1)判定是否有重复的特征函数，而方式2)显然没有。

设ψ(h′)和ψ(g′)分别是m′和p′次本原多项式，且有m+p=n=m′+p′，设针对方式1)产生de Bruijn 序列的特征函数为

综上，结合这4 个圈合并产生de Bruijn 序列的个数为2m+p− 2可知，由定理4 描述的特征函数产生de Bruijn 序列的个数为

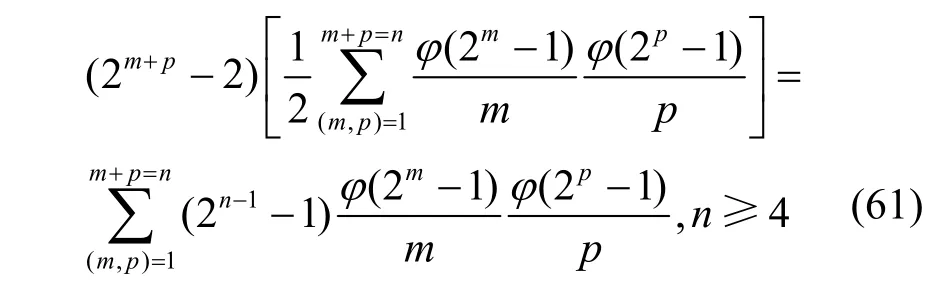
证毕。

由定理4 可知，当圈个数为4的LFSR的特征多项式分解为2 个不可约多项式的情形时，只能通过定理中描述的这几种并圈方式构造de Bruijn 序列的特征函数。结合定理3 与文献[31]的相关结论，本文证明了基于全体圈个数为4的n级LFSR 构造n级de Bruijn 序列的全部数目。定理4 证明过程中，只要求解出n元线性方程组的解，通过任意2 个互素的m,p(m+p=n)级本原多项式，就可以直接得到定理4 中没有重复的且数量庞大的n级de Bruijn序列特征函数。

3 结束语

本文从圈个数的角度，基于LFSR的反馈移位寄存器的级联特征和线性方程的思想，给出了圈个数为4的LFSR的具体数目，从而给出了基于全体圈个数为4的n级LFSR 构造n级de Bruijn 序列的并圈方法，并且得到了其全部数目。该方法可以通过任意2 个级数互素的本原多项式直接构造大级数的de Bruijn 序列特征函数，同时其分析思路也可以进一步丰富和促进LFSR 构造de Bruijn 序列的理论结果。但该方法仍然需要求解一个n元线性方程组，因此在该方法上是否有更具体的de Bruijn 序列特征函数形式，以及在圈个数上是否可以进一步推广将是笔者下一步研究的内容。