交通事故状态下斜拉桥结构响应分析

张 路，王 涛，严 超，朱乐乐，乔可鑫

(长安大学 公路学院，陕西 西安 710064)

0 引言

大跨度斜拉桥在其整个服役期内，发生因人为或自然因素导致的极端事件是不可避免的，而市政斜拉桥运营阶段车流密度大，极易发生交通事故、交通管制等极端事件。值得注意的是，极端事件下车流将发生一系列制动动作，对桥梁产生较大的纵向响应，并可能带来不可修复的损伤。目前针对大跨度斜拉桥正常运营阶段下的结构响应分析研究已较为深入，而对交通事故状态下车流发生连续制动的桥梁结构响应分析少有研究，因此有必要开展交通事故状态下斜拉桥梁结构响应分析。

随着对车辆荷载研究的不断深入细化，国内外学者在随机车流模拟、车辆制动模型等方面进行了大量的研究。郭彤[1]等选用极值I型和2个正态分布函数的加权对统计得到的车辆分布特性进行拟合，并模拟了一般状态与密集状态2种车流荷载；王涛[2-3]等建立了一种车流运行仿真模型，编制了随机车流的仿真模拟程序；赵建峰[4]提出了一种动态称重系统与CCD线阵成像相结合的交通荷载采集系统，对交通量的时变特性和交通量的车道分布特性做了简单统计，并根据荷载特性生成了疲劳荷载谱；袁阳光[5]等利用多重正态分布对动态称重数据的车质量、轴质量和轴距进行了多峰拟合，利用多重指数分布对车头时距进行了多重拟合；FRYBA[6-7]研究了梁在滚动的质量减速作用下的基本特性，进行了车辆制动的精准态分析和施加在轨道与桥梁上的初始力分析；GUPTA 和TRAIL-NASH[8]以桥梁结构坐标与车辆行驶位置坐标为依据提出了一种响应方程，研究了不同路面粗糙度下与车辆制动的三跨变截面桥梁模型的动力行为；YANG[9]等提出了一种基于纽马克有限元差分格式的能够处理各种车桥耦合通用数值方法，可以分析车辆在桥面的正常行驶、车辆制动、车辆跳车等行为；蒲军平[10]等研究了车辆在桥面疾驰过程中突然制动对桥梁产生的影响，对车辆制动过程产生的摩擦力与制动力进行了数值模拟；吕龙[11]等分析了列车制动作用下的结构纵向动力响应，根据获取不同速度参数列车制动力分析列车制动过程中桥梁不同构件的内力位移响应。目前，车辆制动下大跨斜拉桥结构的纵向响应研究主要集中在单车制动，双车制动等单一车载工况，对于交通事故状态下多车道、多车型的随机车流连续制动分析较少，且在进行结构响应分析时未能考虑风车荷载联合作用。

鉴于此，有必要开展交通事故状态下结构响应分析。首先，基于已有风车桥分析系统，建立不同车流密度的随机车流模型，引入车流制动反应模型，建立交通事故状态下的风车斜拉桥耦合振动分析框架；其次，以沿海地区一市政斜拉桥为背景，对主梁进行风场模拟加载，并对车流制动位置、车流密度进行参数敏感性分析；最后，分析不同交通事故工况下，随机车流制动的桥梁关键位置最不利结构响应区间。

1 引入制动随机车流的风车斜拉桥耦合振动分析框架

为实现交通事故状态下风车斜拉桥结构耦合振动响应分析，首先，建立桥梁正常运营阶段下不同车流密度的随机车流模型；其次，建立车流制动反应模型，实现交通事故状态下制动车流模拟，并给出3种交通事故下的随机车流状态；最后，基于已有的风车斜拉桥耦合振动研究，引入制动随机车流，建立交通事故状态下的风车斜拉桥耦合振动分析框架。

1.1 随机车流模型

桥梁正常运营阶段行驶在桥梁上的车流具有很大的随机性，依据已有研究[5]，随机车流统计参数(如车型、车重、车头时距等)服从一定的概率密度分布特征。车头时距一般服从对数正态分布，车型车质量服从均匀分布[12]，参考已有研究的多峰正态分布[13]。依据实测交通流数据[5]，构建3种车流模型：密集车流、一般车流、稀疏车流，假定车流车速恒定，车速分别为40、60、80 km/h，车头时距分别服从ln(VD)～N(4.7,0.9)、ln(VN)～N(5.6,0.56)、ln(VN)～N(6.2,0.38)的对数正态分布。

1.2 车流制动反应模型

为实现交通事故状态下制动随机车流的模拟，建立车流制动反应模型，见图2。基于《公路路线设计规范 JTG D20-2017》[14]中停车视距的规定，驾驶员在受到前方障碍物、车辆制动信号的刺激下，当车间距达到驾驶员心理反应阈值时，车辆将经历2个阶段：驾驶员对刺激信号做出反应，反应时间间隔内车辆按原速度继续行驶；反应时间过后，驾驶员开始制动，车辆逐步减速至停止。因此，车辆的车头时距l由3部分组成：反应距离R、安全距离S、制动距离B。其中，车辆车头时距l按照《公路路线设计规范 JTG D20-2017》选取；反应距离同驾驶员反应时间密切相关，依据美国AASHTO规范选取反应时间为2.5 s；为保证驾驶员不与前方障碍物、车辆相撞，取安全距离为5～10 m；制动距离和制动加速度按式(1)计算。

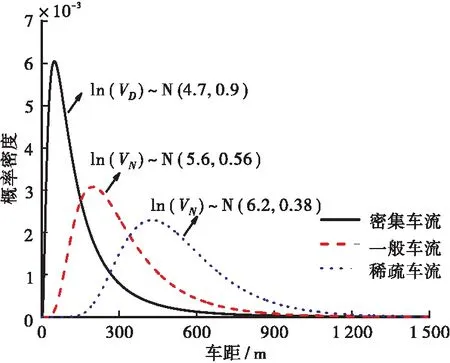
图1 车头时距概率密度拟合曲线

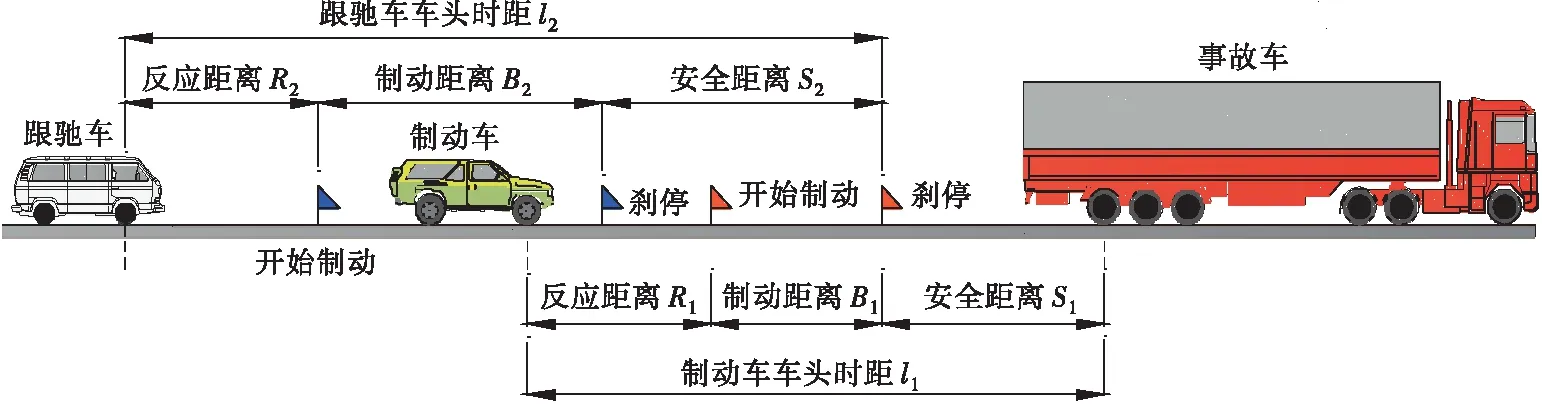
图2 车流制动反应模型

车辆制动距离为车辆开始制动到车辆刹停的距离，即初速度V0减速到零的距离，根据车辆制动反应模型易知制动车的制动距离和制动加速度公式：

(1)

式中：n表示车列中开始制动的第n辆车；Rn表示反应距离；Bn表示制动距离；Sn表示安全距离；ln表示车头时距；vn表示初始速度；an表示制动加速度。

为方便后续结构响应分析工况的建立，将交通事故下的桥梁上随机车流状态分为3类：①单车道车辆发生抛锚、追尾事故，造成单向单车道堵塞，跟驰车辆依次制动，如图3(a)所示；②桥梁单侧行驶方向发生车辆侧翻、多车相撞等严重事故，造成单向多车道行车堵塞，多车道车辆依次制动，如图3(b)所示；③桥梁一侧行驶方向实行交通封闭，另一侧发生车辆侧翻、多车相撞等严重事故，造成单向多车道行车堵塞，多车道车辆依次制动。

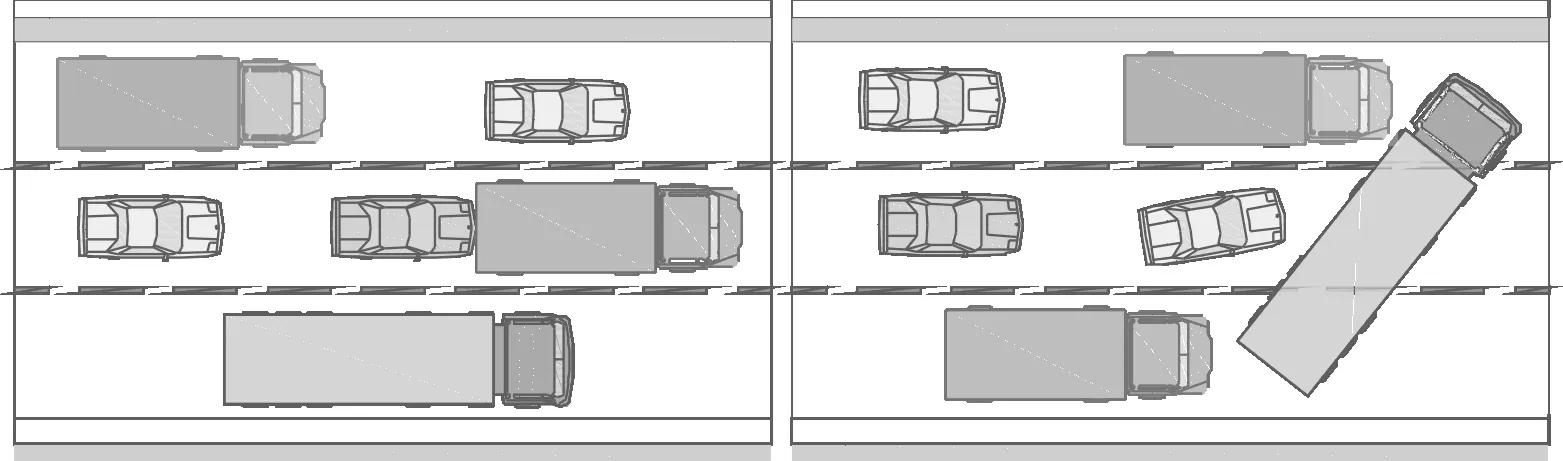
(a) 单向单车道堵塞 (b) 单向多车道堵塞

1.3 引入制动随机车流的风车斜拉桥耦合振动框架

大跨径斜拉桥通常受到风、车、斜拉桥3个基本元素间的交互耦合作用，已有的风车斜拉桥耦合分析系统主要分为3个部分：风桥耦合、车桥耦合与风车耦合。风桥耦合中，风荷载可模拟为3部分：平均风引起的静风力、脉动风引起的抖振力和气动耦合产生的自激力[15]，其中，静风力通常由节段模型风洞试验获得的三分力系数确定，抖振力根据SCANLAN[16]准定常气动公式的求解获取，自激力采用LIN[17-18]等提出的脉冲响应函数计算；车桥耦合中，基于车辆与桥梁间的几何和力学耦合关系实现车桥接触点的位移和接触力的协调；风车耦合中，考虑车辆外形的气动力参数和融合侧滑自由度的车辆动力分析模型，实现车辆在侧风环境下的驾驶偏离响应模拟，最终建立风-车-桥系统耦合运动方程为：

(2)

式中：M、C和K分别为质量、阻尼、刚度矩阵，u表示位移向量；v、b表示车辆和桥梁；Kb表示桥梁刚度矩阵，且Kb=Ke+Kg即弹性刚度Ke和几何刚度Kg；Fbg、Fbst、Fbbu、Fbse和Fbv分别是桥梁自重、侧向静风力、抖振力、自激力、车轮与桥面接触力；Fvg、Fvst和Fvb分别表示车轮自重、车轮准静态风作用力、车轮与桥面接触力。为进一步研究交通事故状态下斜拉桥结构响应，在已有风车桥分析系统[15]基础之上，考虑随机车流的横向位置、制动位置和制动力，建立了考虑制动随机车流风车斜拉桥耦合振动分析框架，见图4。其中，车流横向位置通过车道横向偏心设置；制动位置通过车辆车头时距设置；制动力则采用车辆制动惯性力F=-ma模拟。

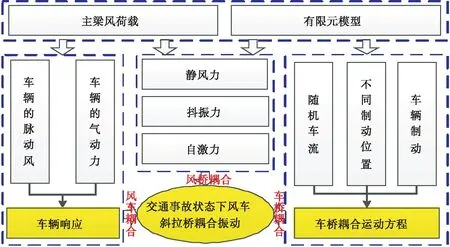
图4 交通事故状态下风车斜拉桥耦合振动分析框架

2 工程背景

为研究交通事故状态下斜拉桥结构响应，选取江苏省沿海地区一座半漂浮体系的市政斜拉桥进行计算分析，其主桥设计为(58+102+360+102+58)m，见图5。设计为双向六车道，设计车速为60 km/h，荷载等级为公路-Ⅰ级。主梁采用混凝土桥面板与钢箱梁的叠合梁结构，斜拉索采用平行钢丝斜拉索。为实现斜拉桥结构响应分析建立全桥有限元模型，见图5。主梁、索塔、桥墩采用空间梁单元Beam4模拟，斜拉索采用空间桁架单元Link10模拟，采用刚臂单元模拟斜拉索与主梁、索塔的连接，桥面系采用质量单元Mass21模拟。采用约束竖向、横桥向线位移自由度的耦合连接模拟塔梁交接处的竖向支座，索塔和桥墩底部采用固结约束模拟。

考虑到交通事故状态下，沿海地区桥梁常受到车辆荷载和风荷载联合作用，为获得更加真实的桥梁结构响应，对主梁进行三维风场模拟，采用谐波合成法选取主梁结构(200个节点)进行风荷载模拟加载，见图5。全桥风场模拟主要参数如下：跨度L=680 m，地面粗糙高度z0=0.01 m，地表粗糙度系数取为0.10，截止频率为ωψ=10π(rad/s)，频率等分数N=2 048，模拟采样时距dt=0.1 s。横桥向和纵桥向风速谱采用Simiu谱模拟，竖向风速谱采用Panofsky谱模拟，跨中模拟点100的风速时程曲线见图6，点100的模拟谱与目标谱的功率谱对比见图7。

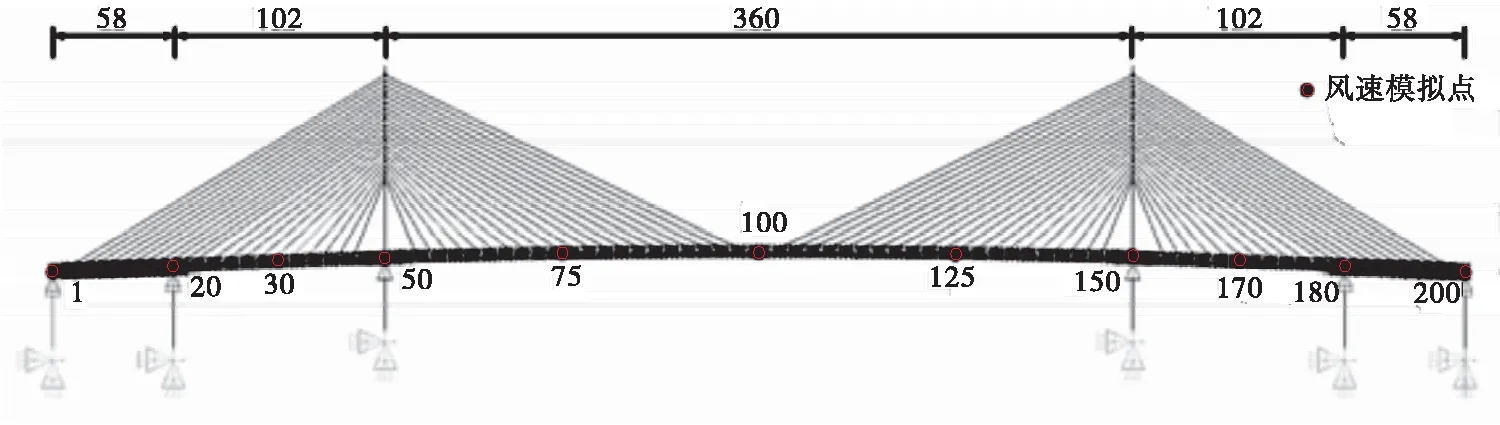
图5 市政斜拉桥(单位：m)

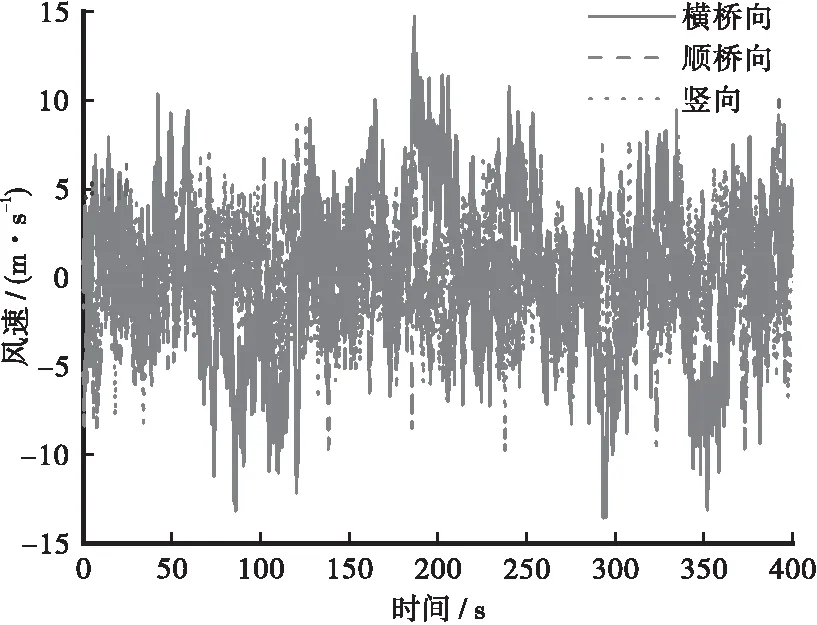
图6 模拟风速时程曲线

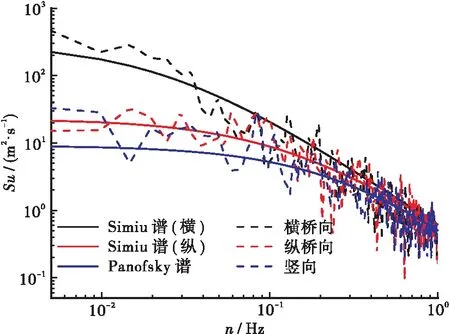
图7 目标谱与模拟谱功率谱

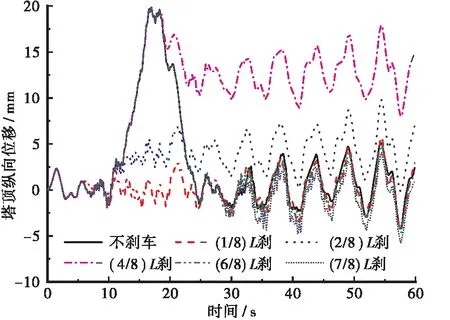
图8 塔顶纵向位移时程曲线

3 参数敏感性分析

考虑到运营阶段市政桥梁不同时段处在不同车流密度状态，且车流制动位置具有随机性，为获得交通事故状态下斜拉桥结构的最不利响应，对车流制动位置、车流密度进行参数敏感性分析，以获得随机车流的最不利制动位置和最不利车流密度。

3.1 制动位置影响分析

为分析车辆制动位置对桥梁关键位置处结构响应的影响，选取6辆重车(50 t)并排同向行驶，车速为80 km/h，分析车辆在不制动工况和在桥梁跨径的1/8、2/8、4/8、6/8、7/8处制动工况下的关键位置(塔顶、梁端、跨中、塔根、最长拉索等)结构响应。限于篇幅仅给出塔顶纵向位移时程曲线，见图8；梁端纵向位移时程曲线，见图9；塔根弯矩时程曲线，见图10；最长拉索索力时程曲线，见图11。

图10 塔根弯矩时程曲线

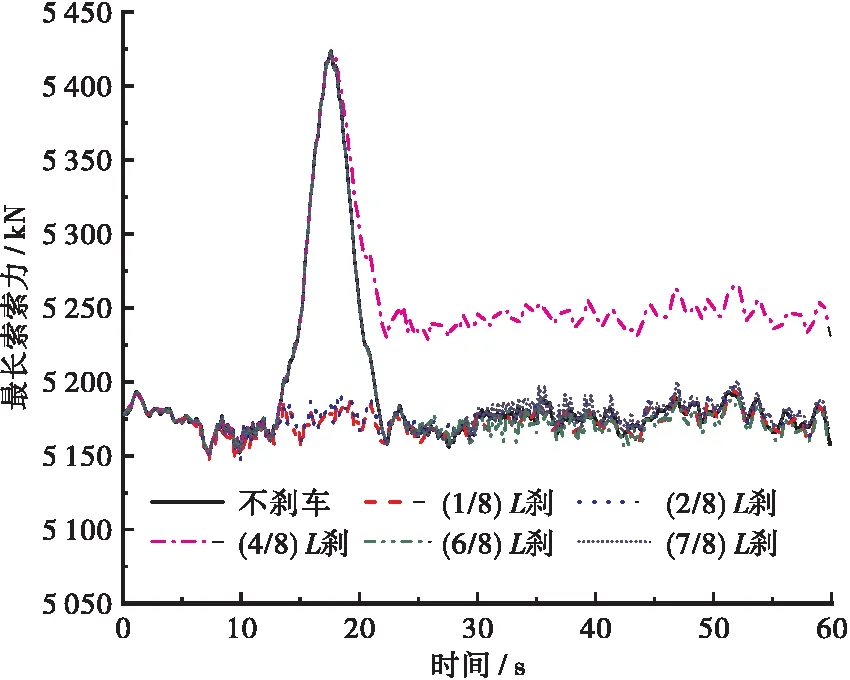
图11 最长索索力时程曲线

由图8、图9可知，车辆制动对塔顶纵向位移时程的影响显著大于梁端纵向位移时程。当车辆在(1/8)L和(2/8)L处制动时，塔顶纵向位移分别在5 mm和0 mm处波动，最大值分别达到5.76 mm和9.79 mm，远小于不制动和其他位置制动工况；不制动、(6/8)L和(7/8)L处制动工况下，车辆制动前塔顶纵向位移时程变化不显著，车辆制动后，时程曲线产生微小变化；当车辆在(4/8)L处制动时，塔顶纵向位移时程变化显著，车辆制动后纵向位移值显著增大并在12.5 mm处波动；梁端纵向位移时程在不同制动位置工况下，变化不显著，最大位移值为(3.43±0.1)mm；不同制动位置对跨中纵向位移影响不显著，最大值均在(3.33±0.15)mm。

由图10、图11可知，车辆制动对最长索索力时程的影响显著大于塔根弯矩时程。车辆在不同位置处制动时，塔根弯矩时程曲线小幅变化，最大值为(10.74±1.7)×103kN·m；当车辆在(1/8)L和(2/8)L处制动时，最长索索力无显著变化，最大值为5 197 kN；不制动、(6/8)L和(7/8)L处制动工况下最长索索力无显著变化，车辆行驶到跨中位置处时，最长索索力达到最大值5 424 kN，随后减小至5 197 kN左右；当车辆在(4/8)L处制动时，最长索索力先达到最大值5 424 kN,随后减小到5 250 kN左右；车辆在(4/8)L处制动时跨中弯矩值达到最大，最大值为14.45×103 kN·m。

综上所述，车辆在中跨跨中制动时对桥梁关键位置处结构响应的影响显著，故该市政桥梁最不利制动位置为(4/8)L处。

3.2 车流密度影响分析

为分析车流密度对桥梁关键位置处结构响应的影响，选取密集车流、一般车流、稀疏车流，车速分别为40、60、80 km/h，选取不同密度车流上同一超车道上的同一(50 t)重车，分析重车在中跨跨中制动时的桥梁关键位置(塔顶、梁端、跨中、塔根、最长拉索等)结构响应。

由图12、图13可知，稀疏车流对塔顶纵向位移时程和梁端纵向位移时程的影响显著大于一般车流和密集车流。密集车流和稀疏车流下塔顶纵向位移最大值分别为45.08和43.87 mm，其中稀疏车流产生的纵向位移时程振幅显著大于密集车流波动；密集车流和稀疏车流下梁端纵向位移最大值分别为22.46和30.05 mm，稀疏车流产生的纵向位移时程振幅显著大于密集车流和一般车流；同样，稀疏车流下跨中纵向位移达到最大值30.37 mm。

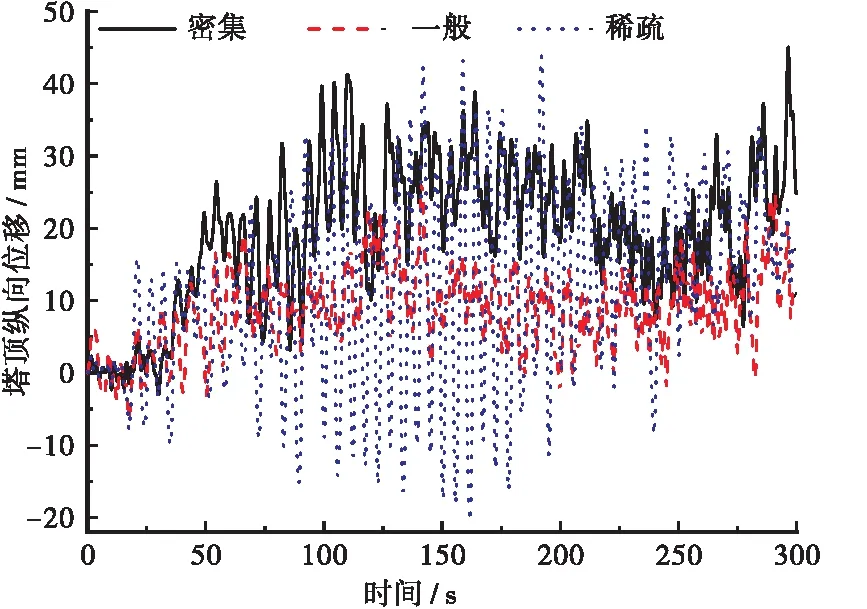
图12 塔顶纵向位移时程曲线

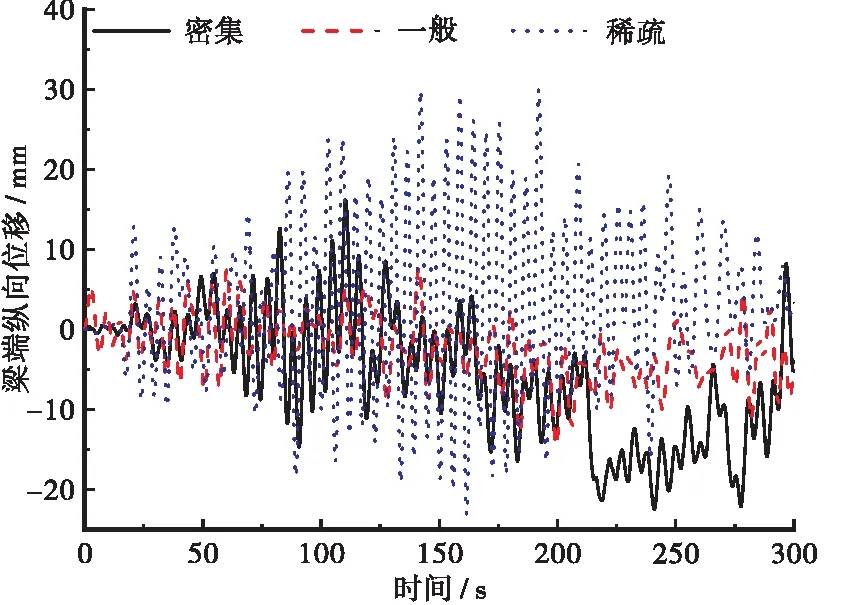
图13 梁端纵向位移时程曲线

由图14、图15可知，密集车流对塔根弯矩时程和最长索索力时程的影响显著大于一般车流和稀疏车流。一般车流和稀疏车流下塔根弯矩变化不显著，最大值分别为17.97×103kN·m和16.39×103kN·m；密集车流车辆制动之前，塔根弯矩同一般车流和稀疏车流基本一致，车辆制动后，塔根弯矩显著增大最大值达到34.57 ×103kN·m；一般车流和稀疏车流下，最长索索力最大值分别为5 397和5 424 kN，而密集车流显著大于一般车流和稀疏车流，最大值达到5 520 kN；跨中弯矩在稀疏车流下达到最大值16.46×103kN·m，密集车流和一般车流最大值分别为12.33×103和12.15×103kN·m。

图14 塔根弯矩时程曲线

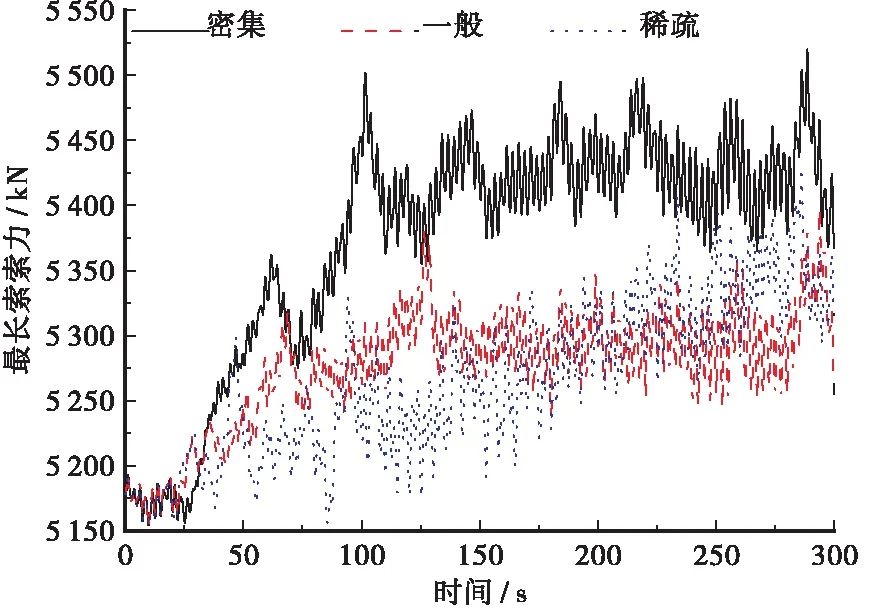
图15 最长索索力时程曲线

综上所述，因稀疏车流车速较高对纵向位移影响显著，密集车流车辆数目较多，竖向荷载较大，对内力影响显著，故该市政桥最不利车流密度为密集车流和稀疏车流，应进一步分析不同交通事故状态下桥梁关键位置最不利结构响应。

4 交通事故状态下斜拉桥结构响应

为进一步分析交通事故状态下斜拉桥的结构响应，基于参数敏感性分析结果，选取密集车流和稀疏车流，且车流中车辆在(4/8)L处制动，并依据1.2节中建立的3种交通事故状态下的制动随机车流模型，计算不制动工况CS1、单车道制动工况CS2、三车道制动工况CS3、单侧封闭下三车道制动工况CS4下的斜拉桥关键位置(塔顶、梁端、跨中、塔根、最长拉索等)结构响应。限于篇幅，仅给出塔顶和梁端纵向位移响应区间，见图16；塔根弯矩和最长索索力值区间，见图17。

图16 塔顶和梁端纵向位移

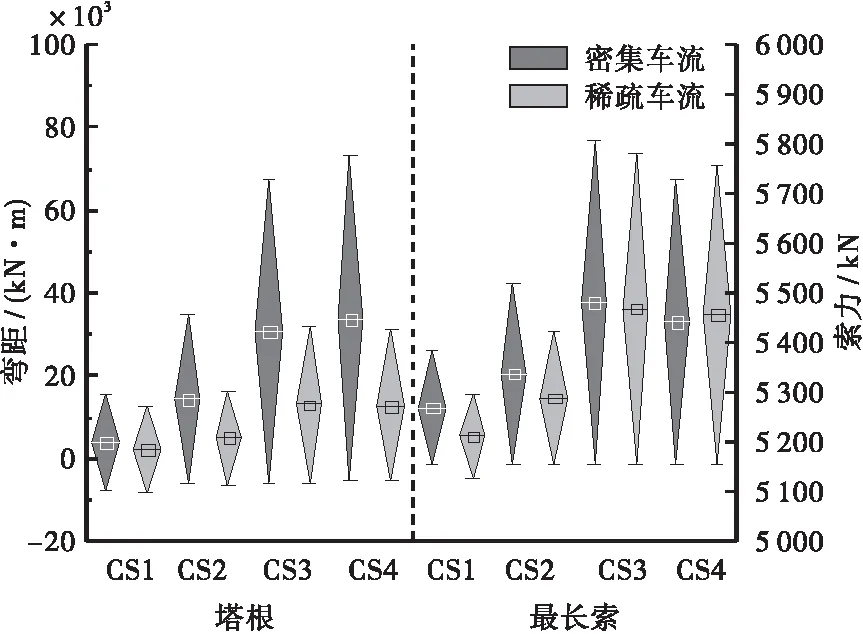
图17 塔根弯矩和最长索索力

由图16和图17可知，CS3和CS4工况下，密集车流对梁端纵向位移和塔根弯矩影响显著大于稀疏车流，而对塔顶纵向位移和最长索索力影响不显著；CS1和CS2工况下，稀疏车流对桥梁结构关键位置纵向位移影响显著大于密集车流，而对塔根弯矩和最长索索力影响小于密集车流；随机车流对塔顶纵向位移影响大于梁端纵向位移，且密集车流CS3下塔顶纵向位移最大值为80.71 mm，梁端纵向位移最大值为-60.14 mm；稀疏车流CS1下对塔顶纵向位移影响显著大于密集车流，其中稀疏车流纵向位移区间为[-28.88 mm,34.85 mm]，密集车流为[-2.99 mm,33.45 mm]；值得注意的是，塔根弯矩值在密集车流CS4下达到最大值73.32×103kN·m，而稀疏车流下最大值仅为32.09×103kN·m；CS3下最长索索力在密集车流达到最大值5 806 kN，稀疏车流下略小于密集车流，为5 783 kN。

综上所述，多车道事故状态下密集车流制动对桥梁结构影响较稀疏车流显著，正常运营状态和单车道事故状态下稀疏车流制动对桥梁结构纵向位移影响较密集车流显著。

5 结语

为实现交通事故状态下斜拉桥结构响应分析，首先，建立了不同车流密度的随机车流模型，并引入车流制动反应模型和不同交通事故状态，建立了交通事故状态下的风车斜拉桥耦合振动分析框架；其次，以沿海地区一市政斜拉桥为背景，进行了主梁风场模拟加载，并对车流制动位置、车流密度进行了参数敏感性分析；最后，分析了不同交通事故工况下，随机车流制动的桥梁关键位置结构响应。主要结论如下：

a.车辆在中跨跨中制动时对桥梁关键位置处结构响应的影响显著，车辆制动对塔顶纵向位移时程、最长索索力时程的影响显著大于梁端纵向位移时程、塔根弯矩时程，车辆在(4/8)L处制动后纵向位移值显著增大，并在12.5 mm处波动，最长索索力先达到最大值5 424 kN，随后减小到5 250 kN左右。

b.稀疏车流对纵向位移时程的影响显著大于一般车流和密集车流，而密集车流对弯矩时程和最长索力时程的影响显著大于一般车流和稀疏车流，稀疏车流下梁端纵向位移最大值为30.05 mm，稀疏车流下纵向位移振幅显著大于密集车流和一般车流，而跨中弯矩在稀疏车流下达到最大值16.46 kN·m密集车流下最长索索力最大值达到5 520 kN。

c.多车道事故状态下密集车流制动对桥梁结构影响较稀疏车流显著，正常运营状态和单车道事故状态下,稀疏车流制动对桥梁结构纵向位移影响较密集车流显著。