半圆形岸边集装箱起重机整机风载荷CFD 数值模拟研究*

罗振国 曾 鹏 林伟华 王碧涛

上海振华重工（集团）股份有限公司 上海 200125

0 引言

由于码头用户对岸边集装箱起重机（以下简称岸桥）运输性能需求的提高，其外形尺寸、载重量也随之加大。在岸桥结构的设计过程中，风载荷的大小对岸桥整机质量、码头轮压有着直接影响。设计时选择合理的构件截面类型，使之能有效降低整机的风载荷，对岸桥整机质量的轻量化及减低码头轮压具有重要意义。

计算流体力学(Computational Fluid Dynamics，简称CFD)是20 世纪60 年代随着计算机科学迅速崛起而形成的，它通过计算机的数值模拟，对流体传动或热传导等物理现象进行数值分析研究的学科[1]。本文将利用流体力学仿真软件Fluent，对半圆形主梁岸桥的整机风载荷开展CFD 数值模拟分析研究。

1 CFD 数值模拟的基本理论

1.1 流体控制方程

在流体力学中，一般以偏微分方程的方式描述流体的流动，这些控制着流体流动的方程常被称为CFD 控制方程，CFD 控制方程主要包括流体流动的质量方程和动量方程。

1）质量方程

任何物理流动都要满足质量守恒定率，即单位时间内流体微元体中质量的增加量等于同一时间间隔内流入该微元体中的净质量[2]，按照这一定律可得出质量守恒方程为

对于不可压缩流体，即密度r 不随时间而变化，式（1）可简化为

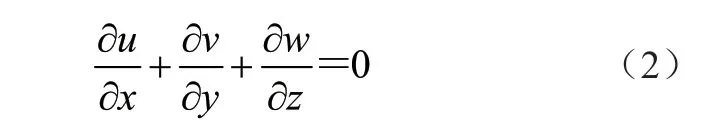
式中：r 为流体的密度，u、ν、w 为速度矢量在x、y、z 方向上的速度分量。

式（1）、式（2）即为流体运动的质量守恒方程，也称作流体运动的连续性方程[3，4]。

2）动量方程

由牛顿第二定律可知，微元体中流体的速度变化率等于该微元体所受的合外力，根据广义牛顿内摩擦定律[5]可以得到流体运动的动量方程（N-S 方程），即

式中：fx、fy、fz为单位质量流体受到的质量力，P为压力，υ 为流体的运动粘度。

1.2 控制方程求解

针对流体湍流控制方程的求解，常用的CFD 仿真软件主要有直接数值模拟法（Direct Numerical Simulation，简称DNS）、大涡模拟方法（Large Eddy Simulation，简称LES）、Reynolds 平均法（Reynolds Averaged Navier Stokes， 简 称RANS)。DNS 方 法 和LES 方法对计算机内存空间及计算速度要求非常高，目前工程领域中最常用的求解方法为RANS 方法，RANS方法又 分 为Standard k-ε、RNG k-ε、Realizable k-ε、Standard k-ω、SST k-ω 等5 种湍流求解模型。

文献[6]针对岸桥风载荷数值模拟中湍流模型的选取，采用以上5 种工程中常用的湍流求解模型对岸桥风场进行数值模拟，并结合风洞试验对模拟结果进行了分析。结果表明，从整体计算情况来看，RNG k-ε 模型更加适合岸桥的风场模拟。本文中对半圆形主梁岸桥进行的CFD 数值模拟将采用RNG k-ε 模型对湍流控制方程进行求解。

2 CFD 数值模拟

2.1 模型建立

本次数值模拟以某半圆形主梁岸桥来建立仿真的三维模型。考虑到一般岸桥风洞试验是以1:100 的缩尺比例来制作实体模型，故本文CFD 数值模拟的三维模型也按1:100 比例来建模。模型的主要尺寸如表1 所示。

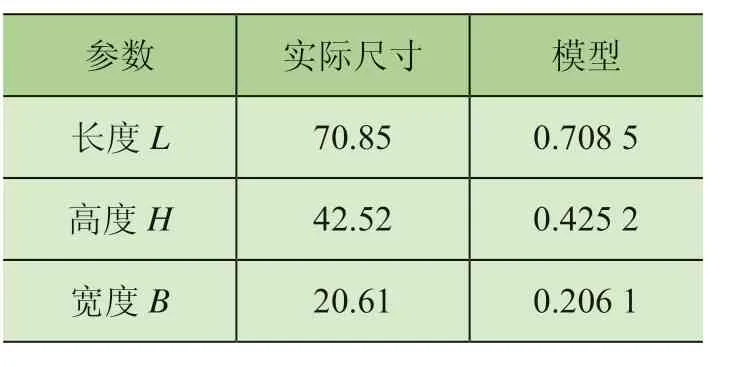
表1 岸桥主尺寸参数 m

本次仿真所用的半圆主梁岸桥的三维模型如图1 所示，岸桥的半圆形主梁实际截面尺寸如图2 所示。考虑到便于提高后续网格划分的质量，对岸桥的模型进行了必要的简化，省略了对整机风载荷影响较小的附属件，也对构件连接处的部分细节进行了简化处理。

图1 半圆形主梁岸桥模型

图2 半圆形截面主梁主尺寸

2.2 网格划分

CFD 仿真的流场计算域采用长方体流域，尺寸如图3 所示。流场入口到岸桥模型的距离为3L，流场出口到岸桥模型的距离为10L，流场域宽度尺寸为6L，流场的高度尺寸为3H。

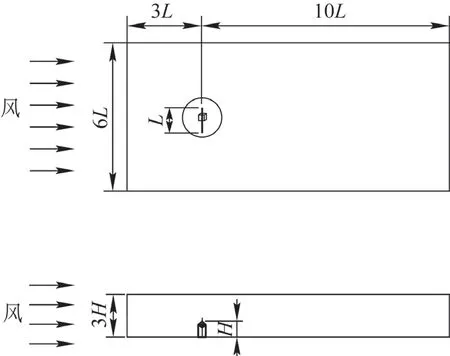
图3 流场计算域尺寸

流场的网格划分主要由靠近岸桥模型附近区域、岸桥周围区域和流场后方区域组成。考虑到在岸桥模型壁面附近的流场变化剧烈，将岸桥壁面附近的网格进行加密处理，流场域网格的划分情况如图4 所示，网格的总数控制在4h 106左右。图5 为半圆形截面主梁岸桥壁面附近的网格划分情况。

图4 流场域网格

图5 岸桥壁面附近网格

2.3 边界条件

图6为CFD 数值模拟的流场边界示意图。流场的入口采用采用速度入口条件，流体为空气，速度为20 m/s，密度为1.225 kg/m3（15℃温度条件下）。岸桥模型表面为固定壁面，流场域四周边界设置为对称边界，可减少外围边界流场对模拟结果的影响，流场出口边界设置为自由出流。由前述可知，采用RNG k-ε 模型来求解流场湍流方程。

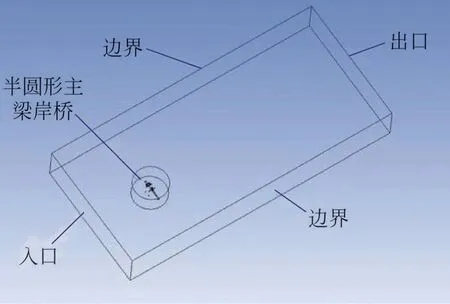
图6 流场边界示意

2.4 数据处理

CFD 仿真模拟的数据处理采用图7 所示风向角及坐标系定义。O-XYZ 为岸桥模型体轴坐标系，OX 为岸桥小车方向由陆侧指向海侧，OY 为岸桥大车方向由面海右侧指向面海左侧，OZ 为高度方向由低指向高；O-XwYwZw为风轴坐标系，OXw为顺风方向指向下游，OZw与OZ 方向一致，OYw的方向由右手法则确定。迎风角度θ 为OXw与OX 之间的夹角，当迎风角度等于0e 时，风从陆侧吹向海侧。风向角θ 的变化范围为0°～180°，计算间隔为15°。

图7 岸桥CFD 仿真坐标系释义

风轴系与体轴系中的力转换关系可表示为

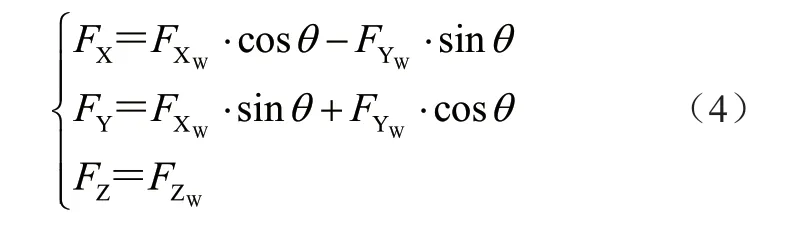
式中：FX、FY、FZ为岸桥在体轴坐标系的3 个方向所受的风力；FXW、FYW、FZW为岸桥在风轴坐标系的3个方向所受的风力，由CFD 数值模拟计算获取。

将CFD 数值计算的结果按式（5）处理，即可得到岸桥整机的风载荷系数为

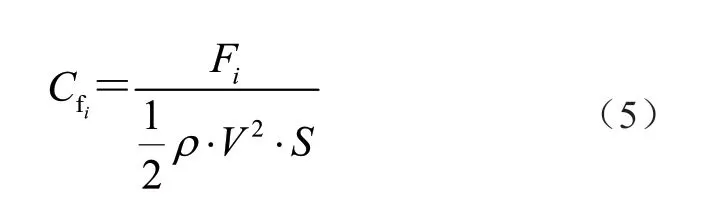
式中：Cfi为3 个方向的风载荷系数，i ＝X、Y、Z；r 为空气密度；V 为空气的流速；S 为无量纲特征参数，S ＝0.1L·H，L、H 取表1 的模型尺寸值。

由文献[3]可知，当雷诺数足够大时，对岸桥在不同风速下的整机风载荷计算可通过任意风速下CFD 数值计算得出的风载荷系数来预测，得到岸桥整机实际风载荷Freal为

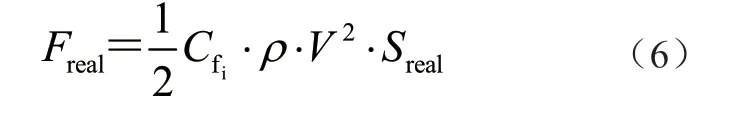
式中：Sreal为无量纲特征参数，且Sreal＝0.1L·H，L、H 取表1 中的岸桥实际尺寸值。

3 结果分析

通过CFD 数值仿真计算，得到图8 ～图10 所示迎风角度为0°、90°、180e 时的岸桥整机构件表面的压力云图。从图中可以看出，随着迎风角度的变化，岸桥构件表面的风压也随之变化。在构件的迎风正面为正压力，而在构件的迎风背面多为负压力。

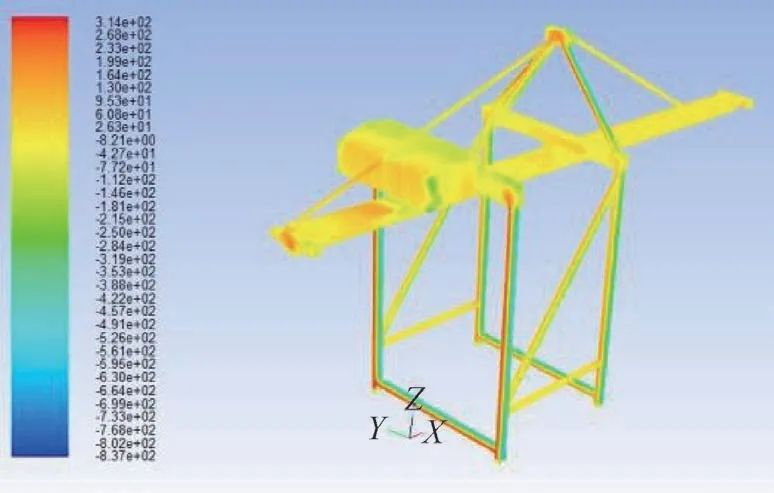
图8 0º时整体压力云图

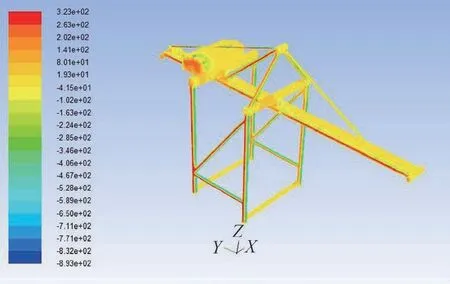
图9 90º时整体压力云图

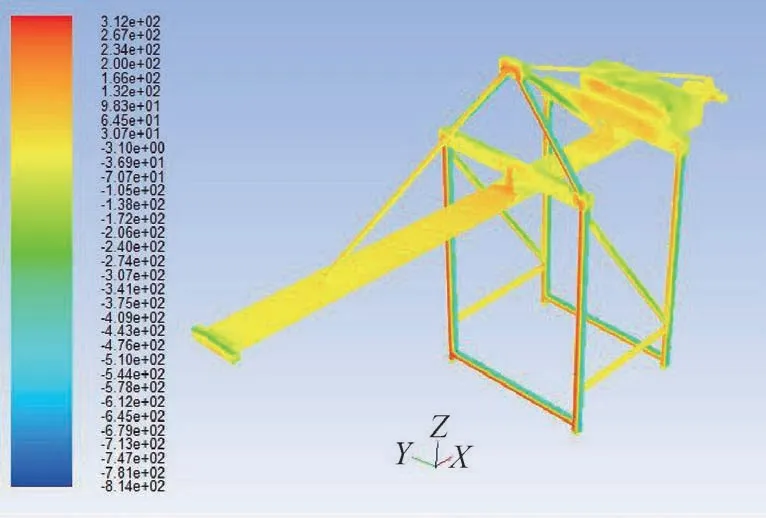
图10 180º时整体压力云图

通过CFD 数值模拟得出的半圆形主梁岸桥的随迎风角度变化的整机风载荷系数如表2 所示，其中风载荷系数为负值时，风载荷合力的方向与图7 定义的方向相反。由于OZ 方向的风载荷较小，实际工程设计中一般不考虑OZ 方向的风载荷，故本文未不列出OZ 方向风载荷系数及对应的风载荷值。

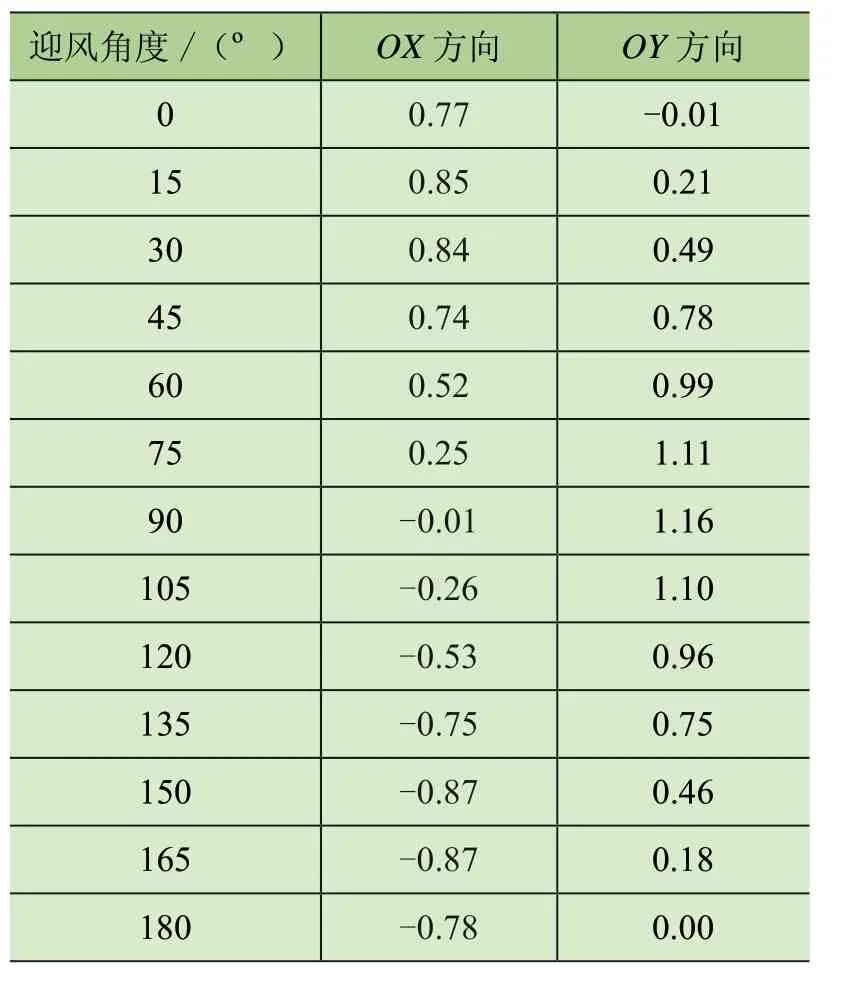
表2 整机风载荷系数

由图11 可知，OY 向的风载荷系数在迎风角为90e时达到最大值，为1.16；在迎风角度为0e 和180e 时风载荷系数最小，接近于0。并且，OY 向的风载荷系数以90e 为分界线接近于对称分布，与岸桥的结构特征相符合。

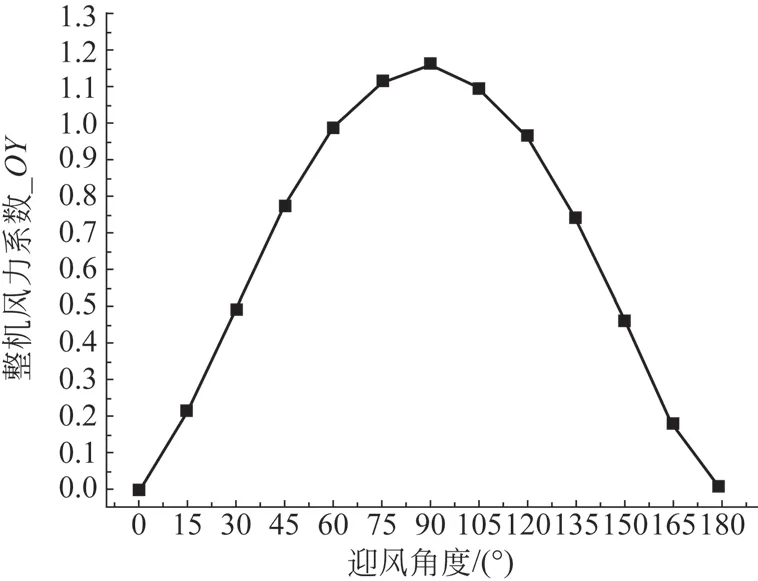
图11 OY 向的整机风载荷系数

图12 为半圆主梁岸桥在OX 方向整机风载荷系数变化趋势图。由图12可知，在迎风角度为15°、165e 时，OX 向风载荷系数达到OX 正向最大或负向最大，与OY向的风载荷系数相似，OX 向的风载荷系数以90e 为分界，呈反对称趋势。

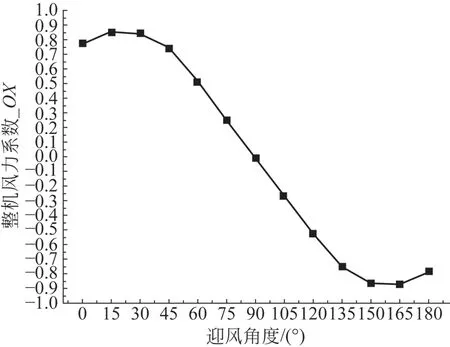
图12 OX 向的整机风载荷系数

根据CFD 数值模拟得出的整机风载荷系数，即可求得半圆形主梁岸桥在不同风速下的整机风载荷。表3为风速为20 m/s 时的整机风载荷，表4 则为风速55 m/s时的整机风载荷。由表3、表4 所示数据可知，CFD 数值模拟计算得出的整机风载荷大小变化趋势与风载荷系数变化趋势一致。

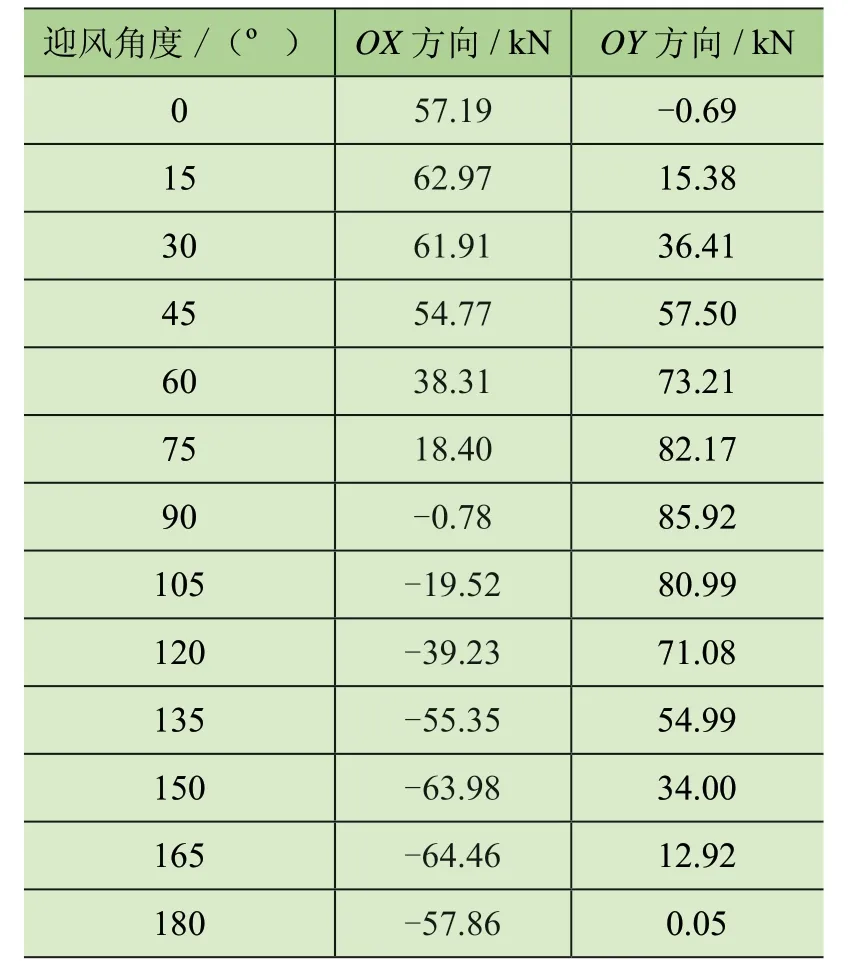
表3 V ＝20 m/s 时整机风载荷

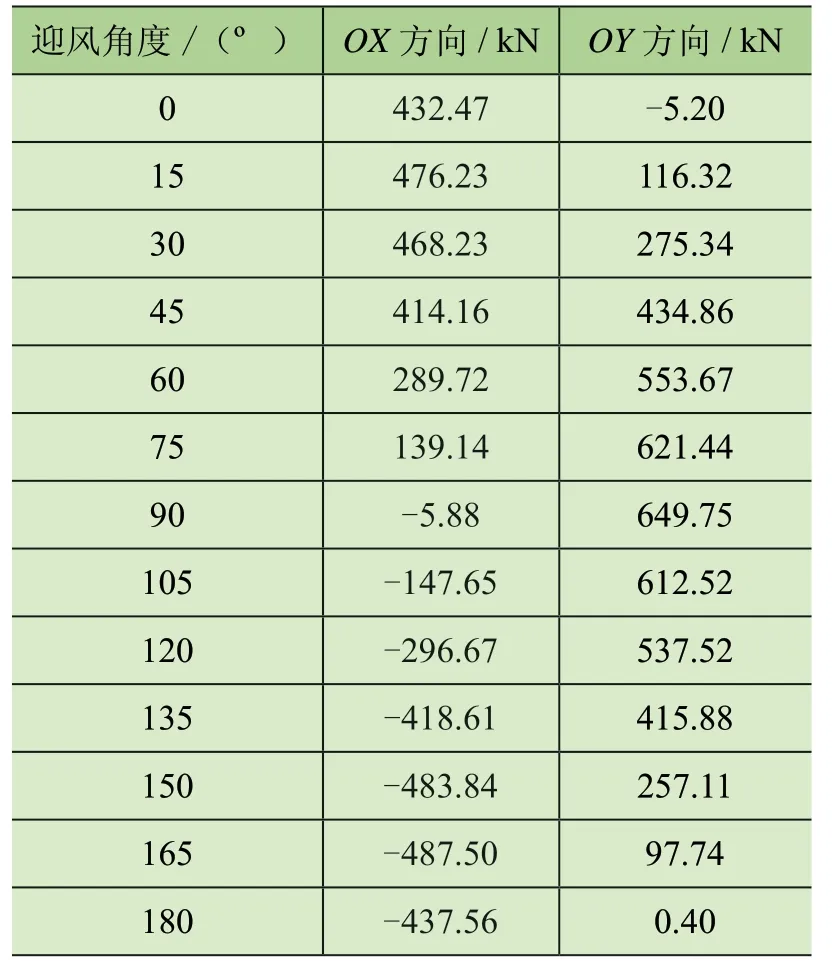
表4 V ＝55 m/s 时整机风载荷

在实际工程应用中，一般通过查阅GB/T 3811－2008《起重机设计规范》[7]中的风力系数，再根据各构件的迎风面积计算出每个构件的风载荷，从而得出整机的风载荷值。将CFD 数值计算得出的整机风载荷与通过设计规范计算得出的风载荷对比，发现在迎风角度为90e 时，CFD 数值计算的结果和规范算出的结果相差不大；迎风角度为0e 时，CFD 数值计算的结果比规范算出的结果小。这主要由于岸桥后主梁上机器房的存在，对陆侧上横梁等部件存在风遮挡效应，而通过规范计算则无法把机器房的遮挡效应等因素考虑进去，所以使CFD 数值计算的整机风载荷结果偏小。

4 结论与展望

1）得到了在不同迎风角度（θ ＝0º～180°）变化条件下的半圆形主梁岸桥整机风载荷系数。OY 向风载荷系数最大值为1.16（迎风角度为90°）， OX 向风载荷系数最大值则为-0.87（迎风角度为165°）。

2）求出了半圆形主梁在风速为20 m/s、55 m/s 时的岸桥整机风载荷，其在迎风角度变化下的风载荷变化趋势与风载荷系数变化趋势一致。

3）本文CFD 数值模拟计算得出的半圆形岸桥风载荷系数及整机风载荷可为后续的实际工程项目设计提供数据参考。

4）后续可对半圆形主梁岸桥进行整机风洞试验，用于对CFD 数值模拟计算的结果进行验证及仿真模型优化。