异质性劳动力集聚对区域碳排放的影响研究

赫永达，林伯强

（1.山西财经大学 统计学院，山西 太原 030006；2.厦门大学 中国能源政策研究院，福建 厦门 361005）

一、引言

在全球气候变暖趋势加剧和节能减排政策的驱动下，我国正积极履行碳减排承诺，力争在2030年前实现碳达峰，2060年争取实现碳中和。然而，我国的能源要素投入总体上仍表现为高碳化特征，并且这种以煤炭和石油等化石能源消耗为主的能源使用结构在相当长时期内并不会发生根本性的改变。［1］尤其是伴随着中国经济由高速发展向高质量发展的转型，劳动力大规模跨区域流动，在加速了地区城镇化和工业化的同时也诱发了地区资源短缺、环境恶化、碳减排政策失效等问题。如何改善劳动力、能源等生产要素的市场配置效率已成为中国经济实现绿色低碳化发展所亟须解决的问题。因此，研究异质性劳动力跨区域流动与地区碳排放之间的影响机制及其时空演化态势对我国产业结构升级与低碳减排协调发展具有重要意义。

目前学术界对劳动人口和碳排放之间关系进行研究主要从两个角度切入。第一种研究思路以STIRPAT模型为理论基础分析人口结构对碳排放的影响。在早期研究人口结构和碳排放的研究中，学者主要集中讨论人口密度和规模对人口结构的影响，［2-4］并进一步延伸至人口结构与碳排放之间的关系。该种思路需要先验设定人口规模对碳排放是单位弹性的。如果人口规模对碳排放的弹性不满足单位弹性假设，则以此为基础的环境库兹涅兹曲线不再成立。遗憾的是这样的先验设定并没有获得任何实证检验，尤其在人力资本积累达到一定程度时，不同技能结构的劳动力集聚及其引致的地区资本深化程度是不同的。［5-6］换言之，“人口规模对碳排放的单位弹性假设”会随着技能型劳动力规模效应的体现而不再成立。由此，Richard York 等为克服该局限提出了STIRPAT 模型，认为人口、技术和财富对碳排放是非固定比例的随机影响。［7］然而，基于STIRPAT 模型框架的研究，对单纯的时间序列、不同国家的面板样本、中国不同地区的省级面板样本进行实证检验时，目前并没有就劳动力规模、劳动力结构等人口因素对碳排放的影响形成一致的结论。［8-11］

第二种研究思路则是从产业结构角度出发。由于地区产业结构差异决定了地区劳动力雇佣结构的不同，整体而言工业劳动碳排放水平必然高于农业和服务业碳排放水平。因此，这类文献的聚焦点在于揭示异质性劳动力集聚对地区产业结构变迁产生的影响，认为碳排放变化表面上来看是产业结构变迁造成，实际上则由劳动力结构决定。［12-13］该种研究思想得到了众多实证研究者的验证。如孙振清等测算了不同产业结构背景下，创新劳动力和技术创新水平对碳排放效率的影响；［14］王勇等、张同斌等、朱佩誉和凌文基于投入产出模型，模拟了不同产业结构下中国碳排放水平和碳达峰路径；［15-17］周亚军和吉萍利用空间计量模型验证了产业升级过程中地区间要素配置及其空间溢出效应对碳排放影响。［18］

通过对上述文献的梳理，发现关于劳动人口和碳排放之间关系的研究存在以下两点仍值得进一步探讨。首先，现有文献往往忽视了劳动力流动这一典型特征事实。中国改革开放和加入WTO 以来，地区间经济差距逐渐显现，其中一个明显的特征是东部沿海地区依靠先发优势，率先完成了经济增长由传统的“要素驱动”到“技术模仿驱动”再到“创新驱动”的逐步过渡。其造成的直接后果就是劳动力从农村向城市、从内陆地区向沿海地区大规模转移，且人口红利逐渐由丰富转向匮乏再到消失（见图1 和图2）。按照现有关于劳动力规模和碳排放水平之间关系研究的结论推断，地区碳排放水平的提高理应随着人口红利的消失而停止。然而上述预期在实际生产过程中并没有发生，劳动力流动规模与地区碳排放之间究竟是单调的线性关系还是复杂的非线性关系，现有文献尚未对此给出确切的答案，尤其是结合现有关于产业结构和碳排放之间关系的研究成果来看，劳动力流动常常对应着产业结构的变迁。由此，揭示异质性劳动力集聚及其造成的地区产业结构调整是指明地区人口结构和碳排放关系的关键因素之一。

图1 地区城镇劳动数量（万人）

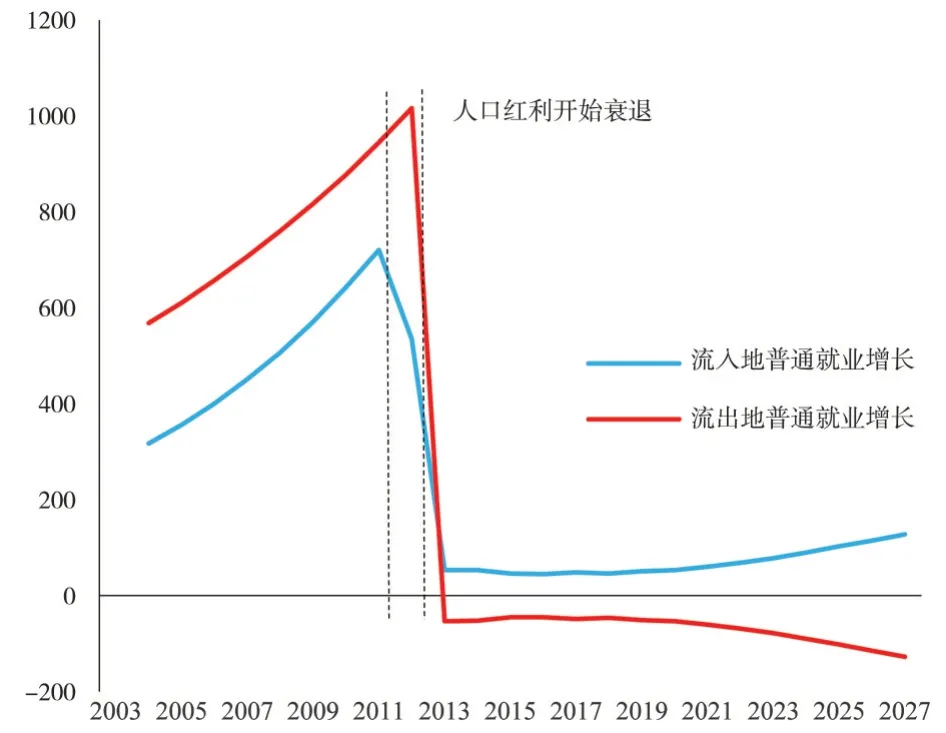
图2 地区就业水平（万人）

其二，对于地区劳动力结构和碳排放之间关系的研究，目前鲜有文献关注异质性劳动力流动这一关键事实。从异质性劳动力流动与地区产业结构和碳排放水平之间关系来看，异质性劳动力集聚对地区产业结构调整的影响不同，技能型劳动力集聚必然促进产业结构高级化，无论是能源利用率还是能源使用水平均有助于碳减排；从异质性劳动力流动与地区技术水平和碳排放水平关系来看，技能型劳动一方面能够在较大程度上促进技术进步，进而反向推动能源利用效率的提高，另一方面能够诱发技术性要素对能源、非技术性生产要素之间的替代，进而减少能源的使用，控制碳排放水平；从异质性劳动力流动与劳动力结构和碳排放水平之间关系来看，技能型劳动力与技术进步、要素替代、碳减排之间的内生反馈机制并不是无限循环的。一方面技能型劳动力集聚会提高地区生活成本，厂商必然会扩大资本和能源的使用，平衡由技能型劳动力集聚造成的简单生产要素（低成本劳动力）的挤出，另一方面，产业相依性决定了技能型劳动力和高技术产业并不能够脱离低端产业而集聚。［5］［19］最终，异质性要素集聚和碳排放之间的关系应是上述几种作用力的相对均衡。

鉴于上述分析，本文拟构造两地区、三部门的一般均衡模型，从理论上揭示异质性劳动力集聚对碳排放的作用机制。本文可能实现的创新之处在于：首先，通过区分高碳排产业和传统服务业，将异质性劳动力流动和资本流动方程纳入一般均衡框架，构建能够描述异质性劳动力集聚特征的一般均衡模型；其次，本文对理论模型的关键结论进行参数校准和数值模拟，结合理论框架和数值模拟结果，从理论上阐明异质性劳动力流动和地区碳排放之间的作用机制和演化特征；第三，本文采用两区制空间杜宾模型，结合中国省级宏观数据，对异质性劳动力流动过程中可能存在的异质性空间溢出效应及其对地区碳排放的影响进行量化检验。通过上述工作，力图对异质性劳动力集聚和地区碳排放之间的内在机制和实际运行规律做出关键性阐述。

二、碳排放理论模型设定

如前文所述，解释异质性劳动力流动与地区碳排放之间内生机制的关键在于厘清异质性劳动力流动及其引致的资本流动速度之间的相互关系，由此判断地区资本深化演化趋势，最终传导到要素配置决定的要素密集型产业结构调整规律。由此，本文在Dissou和Horvath等学者模型基础上构建了包含代表性家庭、低排放行业（传统服务业）、高排放行业（现代工业）的三部门一般均衡模型。［20-21］具体而言，将劳动力划分为技能型劳动力、非技能型劳动力，其中非技能型劳动力从事普通生产和服务业生产，技能型劳动力更多地作为技术载体。这样做的目的在于，不同劳动力对应着不同的资本——劳动力替代规则，而地区资本深化则是决定碳排放的关键因素。由此，通过对异质性劳动力和资本流动的刻画，映射到地区产业结构调整和地区碳排放结构动态变迁，以此揭示地区间异质性劳动力流动和碳排放之间的内生传导机理。

考虑一个包含两地区（地区s和n），且工业品（CMt）和服务产品（CBt）共存的经济体。工业品厂商雇佣技能型劳动力（Ht）、非技能型劳动力（Lt）、使用可变资本（Kt）和能源（Et）进行生产，服务产品厂商雇佣简单劳动力（Jt）、使用固定资本（F）进行生产。劳动力市场的价格信号（工资差距）决定了异质性劳动力的跨区域流动，资本市场的价格信号（利率差距）决定了资本的跨区域流动。

1.碳排放

石油、煤炭、天然气等能源在生产消耗过程中会排放CO2。考虑不同种类的能源在消耗过程中排放的CO2数量不同，因此参照张同斌等的做法，［17］设定煤炭在生产过程中的排放系数为θcoal，石油和天然气在生产过程中的排放系数为θoil，则工业碳排放emt方程可表示为：

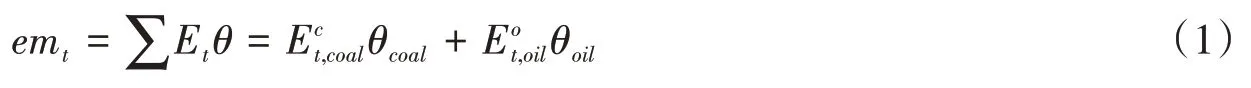
emt表示t期工业碳排放总量表示工业使用煤炭等能源总量表示工业使用原油、天然气等能源总量；θcoal和θoil则表示相应能源在生产过程中的碳排放转换系数。

2.高碳排行业生产行为

设定每个地区只存在一个典型加总的工业厂商。本文设定工业生产技术满足C-D 生产函数形式，并以资本和劳动份额参数之间的差别描述地区间不同要素密集程度的差异：

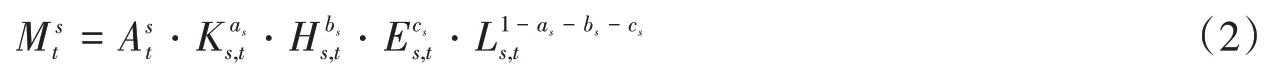
为s（s∈A,B）地区工业厂商在t期的总产出，Kst、Hst、Lst和Est分别表示该地区工业厂商使用的总资本，雇佣的可流动技能型劳动力和可流动非技能型劳动力总量以及使用的能源总量；At表示地区的技术水平；as、bs、cs和（1-as-bs-cs）分别表示资本、技能型劳动、能源和非技能型劳动对工业产出的贡献份额。

3.低碳排放厂商生产行为

根据传统D-S框架，假设服务产品生产表现出显著的规模报酬递增特点，且满足垄断竞争条件。服务产品厂商雇佣可流动劳动力Jit以及使用相应的固定投资Fi提供不同种类的服务产品。除此之外，设定每个地区的市场存在qt个服务产品厂商，每个厂商生产存在一定差异的服务产品。假设每个服务产品厂商采用线性生产技术进行生产，每个厂商的产出xit与使用的固定资本Fi和可变劳动力Jit满足线性生产技术：

Jit为厂商i雇佣的普通劳动力数量；Fi为单个厂商所使用的固定资本投入（假设不存在资本折旧）；aT为产品转化效率。

设定地区存在qt个差异性服务产品厂商。根据D-S条件，每个服务产品厂商生产的服务产品数量cit以及居民消费的“打包”服务产品数量CBt之间关系满足：

ρ为每种服务产品之间的替代弹性。根据居民支出的约束条件，得到居民购买“打包”服务产品和每个服务产品厂商制定的出厂价格之间关系为：

假设服务产品厂商i提供xit单位的服务产品，均衡条件下地区居民对服务产品总量的需求等于地区服务产品总供给，即：

σ＞0 为相对风险规避系数①关于σ数更加详细的说明见后文居民偏好部分。数理模型推导可向作者索要。；Ot为地区总人口Ot=Ht+Lt+Jt。将公式（5）关于服务产品价格的关系式代入公式（6），求得服务产品厂商i供给xi,t为：

当商品完全同质不存在差别情况下，pi=p，xi=x。同时，由于M商品可自由贸易，则M商品价格满足一价定律。出于计算简便考虑，假设同一市场内部不存在商品运输成本，则PM价格可作为价格基准，即PM=1。那么地区单个服务产品厂商的产出可进一步化简为：

关于服务产品厂商制定的出厂价格和支付劳动工资的求解，根据厂商0 利润条件，厂商的全部利润用于支付普通劳动工人的工资，即Rt=ptxt=ptct=·Jt。将厂商产出方程（8）代入0 利润条件，可得厂商支付的工资水平为：

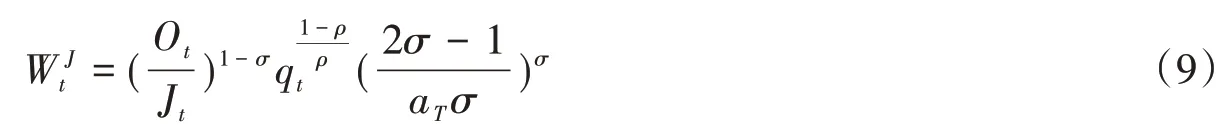
4.异质性劳动力流动与碳排放

在实际要素流动过程中，要素的流动规模取决于地区间相应要素收入差距以及地区间生活成本差距。假设地区间生活成本以地区间不可贸易的服务产品价格、可贸易的工业品价格和不可贸易的住房价格表示。定义异质性劳动力的实际工资差异形式为：

表示s地区技能型劳动力的实际工资水平表示s地区非技能型劳动力的实际工资水平；

表示s地区普通劳动力的实际工资水平。而表示s地区技能型劳动力的名义工资水平；表示s地区非技能型劳动力的名义工资水平；表示s地区普通劳动力的名义工资水平。技能型劳动力和非技能型劳动力的名义工资水平分别为其对产出的边际贡献，普通劳动力的名义工资水平由（9）式决定。由此，异质性劳动力跨地区流动的决策决定于地区间实际工资差异，［22］那么流入地区（不妨标记s地区为流入地区）异质性劳动力的动态积累方程分别为：

h为技能型劳动力的自然增长率，n为非技能劳动力和简单劳动力的自然增长率；ψh、ψl、ψj分别为技能型劳动力、非技能型劳动力和普通劳动力对地区间相应劳动报酬率缺口的反应敏感系数；为流出地区在t时期技能型劳动力数量，为流出地区在t时期非技能型劳动力数量为流出地区在t时期普通劳动力数量。上述三个劳动转移方程表明：地区间劳动的实际工资差距（名义工资和价格水平）是决定相应劳动力流动的根本因素。

与劳动力流动方程类似，资本的转移同样受到两地区间利率差异的影响。与劳动力流动所不同的是，由于利率本身代表货币的价格，因此资本是否转移取决于地区间名义利率。则资本动态方程的化简形式为：

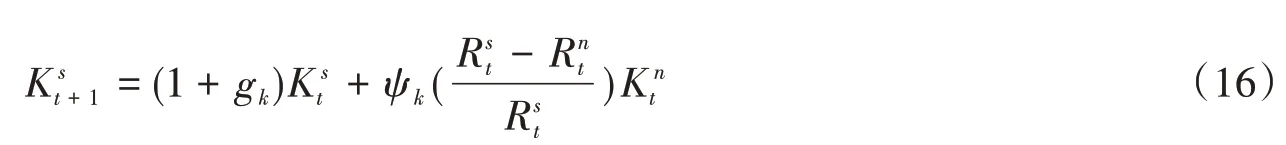
gk为资本积累速度；ψk为资本对地区名义利率缺口的反应敏感系数为流入地市场利率，为流出地市场利率水平；为流出地资本数量。

流出地要素积累方程与流入地要素积累方程对应，只需要将自然增长率后面的转移部分改为负号即可。［5］

结合碳排放方程（1）以及要素流动方程（13）、（14）、（15），能够得到地区碳排放总量和异质性劳动力流动之间的关系为：

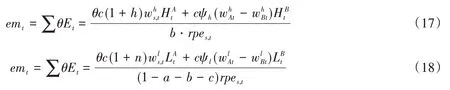
式（17）、式（18）即为以技能型劳动力和非技能型劳动力数量表示的流入地区碳排放水平的函数①流出地区只需将分子第二项加号改为减号即可。。从上述方程来看，发现技能型劳动力和非技能型劳动力对地区碳排放影响机制存在差异：技能型劳动力更多通过单位劳动力碳排放的垂直效应来影响地区碳排放水平（技能型劳动力工资水平和地区间工资差异较大），而非技能型劳动力则主要通过碳排放的规模效应影响地区（非技能型劳动力工资水平较低但规模较大）。通过对比地区碳排放和异质性劳动力之间关系，进一步能够发现：有效采用技能型劳动力和资本对非技能型劳动力进行替代，能够极大地降低碳排放的规模效应。

5.居民偏好

出于简单且不失一般性的考虑，本文假设不同群体的居民均具有不变跨期替代弹性的消费偏好，其根据市场利率和工资水平提供相应的资本和劳动力。每类代表性家庭均追求终生效用最大化。为了便于分析，设定每个代表家庭均供给一单位相应劳动力获得工资收入，并根据市场价格在储蓄和消费之间权衡。因此，不同群体在相应收支约束条件下的效用函数①除了要素流动方程外，流入地和流出地的其他所有方程形式完全一致。因此为了写作的便利和模型形式的简洁，本文所建立的模型，除需特殊备注说明，所有方程只写出流入地相应方程的表达形式，并略去各变量表示地区的下标。可表示为：

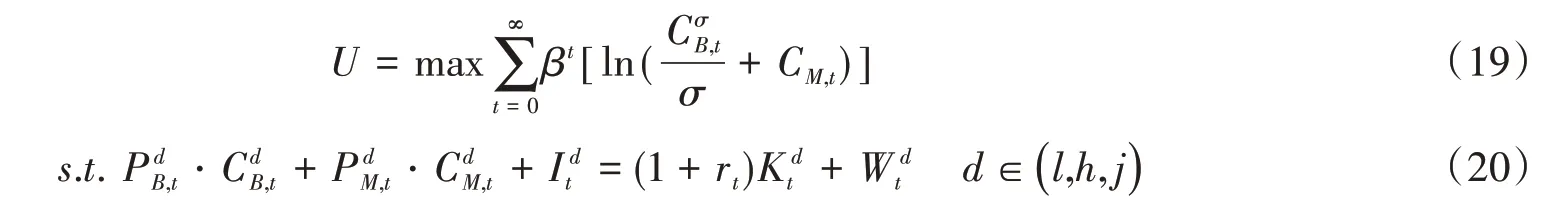
和分别为d居民群体在t期对不可贸易的服务产品、可贸易的工业品和住房的消费数量；为d居民投资水平为相应的资本存量；为d居民群体获得的名义劳动收入。由于假定每个居民固定供给1单位劳动，因此每个居民的劳动收入等于市场工资率；rt为市场利率；β为主观贴现因子；σ＞0为相对风险规避系数；γ为实物资产的效用偏好弹性。在收支约束下最大化居民终身效用，可求得居民d对相应商品的需求为：

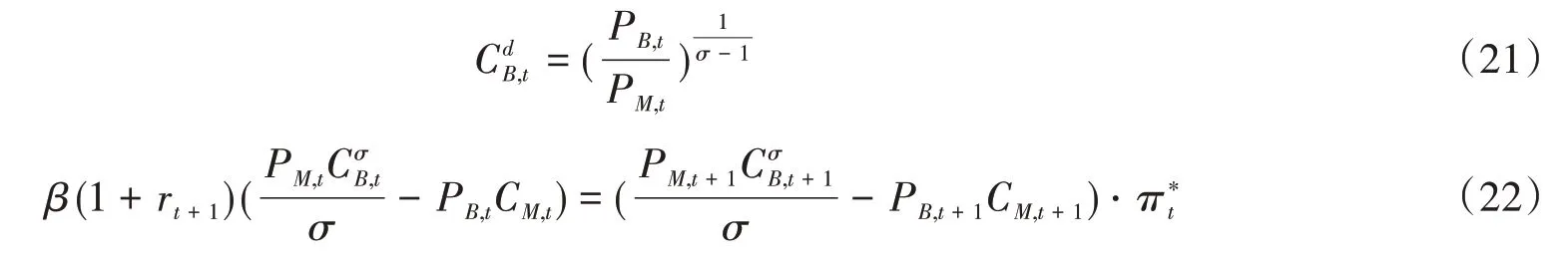
三、参数校准与数值模拟

为揭示异质性劳动力流动与地区碳排放之间的关系，针对第二部分的理论模型，根据求解出的均衡条件进行数值模拟。揭示异质性劳动力和地区碳排放之间的关键机制在于厘清因异质性劳动力流动造成的要素配置变化（资本深化）以及产业结构变化（高碳排放产业结构变化）。对此本节对异质性劳动力流动特征、异质性劳动力流动造成的产业结构变迁和资本配置分别进行数值模拟，并对异质性劳动力流动造成的地区间碳排放规模演变特征进行数值计算。数值模拟的主要目的在于揭示异质性劳动力流动这一典型的内生经济现象与产业结构调整、碳排放结构变迁之间存在的必然联系，对定量分析并不作过分苛刻的要求。

1.参数校准

为了在极大程度上使本文设定的理论模型模拟结果与中国经济发展现实相契合，本文对理论模型中的参数和状态变量的初始赋值按照以下规则校准。

关于工业生产函数的参数校准，要素产出弹性可以根据要素收入份额占总产出比率近似求得。本文细分了异质性劳动力，将本科及以上学历作为技能型劳动、其他学历水平的劳动作为非技能型劳动力和普通劳动力（技能型劳动力和普通劳动力假设为同质，只不过雇佣对象不同）。参照傅晓霞和吴利学的研究成果，［23-24］以此校准的流入地资本产出弹性as=0.43，流出地资本产出弹性an=0.41；流入地技能型劳动力产出弹性bs=0.24，流出地技能型劳动力产出弹性bn=0.21；对于能源对工业产出份额参数的校准，通过投入产出表中第一象限基本流量表的原始数据，计算能源对工业的中间投入系数c=0.17；流入地非技能型劳动力产出弹性（1-as-bs-c）=0.18，流出地非技能型劳动力产出弹性（1-an-bn-c）=0.15。

关于CO2排放系数，借鉴联合国政府间气候变化委员会（IPCC）公布的测算方法、陈诗一和张同斌等的测算方法，［17］［25］对不同能源燃烧利用率和排放系数进行加权处理计算，校准得到煤炭行业的碳排放系数θcoal为2.8①1公斤煤炭燃烧后排放2.8公斤CO2，石油、天然气的排放系数意义同此。，石油和天然气行业的综合碳排放系数θoil为2.1。

关于服务业②具体参数校准过程中，校准的“服务业”具体包括运输和邮电、住宿和餐饮业、旅游业、教育、卫生、社会服务、公共管理社会保障及其他服务业。需要指明的是，本文所指的服务业旨在表明该行业提供的服务不可跨地区贸易。因此，诸如运输和邮电业，尽管该行业存在跨地区业务往来，但其提供的物流服务本质上也是本地服务的一种。生产函数的参数校准，根据相应行业产出、劳动力数量以及固定资本形成总额，设定地区服务业固定资产使用总额Fs=Fn=300，产品转化效率aTs=aTn=0.3。两地区之间各个服务产品厂商生产技术和生产规模并不存在差异，影响服务产品出厂价格的主要因素源自地区对不可贸易的服务产品的需求。［26-27］此外，根据目前研究的一致取值方式，设定异质性消费品之间的替代参数ρ=4。

对于本文居民偏好等参数校准，首先设定主观贴现因子β=0.99；根据相关研究以及经济事实经验，设定资本的稳态增长率按照固定资产投资增长率的平均数取值为0.15；［28］由于居民的消费偏好参数难以直接获取或校准，绝大多数关于发达国家的宏观研究中风险规避系数设定为0.5，由此求得居民个体的主观贴现率取值在2%～4%之间。考虑中国居民储蓄倾向较高，因此本文设定中国家庭的风险规避系数为σ=0.55。

本文要素流动方程的参数校准可分为两部分。对于异质性劳动力的自然增长率的校准，由于本文设定的模型区分了劳动力技能水平存在异质性，近似地认为普通劳动力的自然增长率约等于地区户籍人口的自然增长率，因此对于非技能型劳动力和技能型劳动力，近似地认为其平均增长率n=0.01；针对技能型劳动力的测算③在针对技能型劳动自然增长率测算过程中发现平均数较高主要源于2009-2013 年高校扩招所致。技能型劳动近些年的增长率趋于稳定，流入地区的增长率稳定在2%左右，而流出地的增长率则不足1%。由于本模型的目的并不在于做精确的数值模拟，而是通过构建合理的模型，对地区间劳动流动所展现出的规律做理论上的分析，因此本文在数值模拟过程中，取2003-2018 年间技能型劳动的平均数作为技能型劳动的增长率。，将本科及以上学历水平的劳动力作为技能型劳动力，通过对地区高校招生人数的近似估算，技能型劳动力的平均增长率h=0.02。而对于异质性劳动力跨区域流动系数的校准，本文按照最小偏误的原则，设定技能型劳动力对相应工资差距的流动敏感系数为ψh=0.05、非技能型劳动力对相应工资差距的流动敏感系数为ψl=0.03、普通劳动力对相应工资差距的流动敏感系数为ψj=0.03、资本对利率差距的流动敏感系数为ψk=0.05。

关于生产要素的初始值，按照各地区统计局发布的统计年鉴以及《劳动与就业统计年鉴》公布的数据，取流入地区技能型劳动力初始值=140、流出地区技能型劳动力初始值=150；流入地区非技能型劳动力初始值=1 400、流出地区非技能型劳动力初始值=2 000；流入地区普通劳动力初始值=1 400、流出地区普通劳动力初始值=6 000（单位均为万人）；关于资本存量的初始值，参照张军利用永续盘存法，［29］计算出2004 年流入地工业资本存量=48 000、流出地工业资本存量=73 000（单位均为亿元）。

上述参数的校准以及相应变量初始值取值，所涉及的基础数据源于中国统计局发布的《中国投入产出表-2018》《中国统计年鉴》《中国能源统计年鉴》《中国人口和就业统计年鉴》以及《中经网统计数据库》。

2.数值模拟

本文通过模拟地区产业结构（地区工业产出占总产出的比重）、地区工业产出比（流入地和流出地工业产出比）、地区要素流动规模（技能型劳动力、非技能型劳动力和资本流动规模）、地区劳动技能结构（各地区技能型劳动力和非技能型劳动力比值）和地区人均资本深化程度（各地区劳均资本存量）等指标，对地区间异质性劳动力流动和产业结构调整之间规律进行刻画。

本文首先模拟了地区间要素流动特征（见图3）。从技能型劳动力流动特征来看，技能型劳动力从技术劣势地区向技术优势地区的流动规模会逐渐减少，在可以预见的未来（40 期模拟期后），地区间技能型劳动力甚至可能出现回流的趋势。造成这样的原因在于：首先，技术优势地区的资本回报率更高，因此在规模报酬不变的前提下，工业劳动对产出的贡献更小。这也就造成了逐利行为会使得资本大规模从技术劣势地区向技术优势地区流动，资本流动一方面造成了地区工业进程加快，在产业相依性的约束下，若流入地区服务业无法同规模扩张，则工业扩张的一个必然结果是地区服务业价格上升、生活成本提高，从而对地区工业劳动力和服务业劳动力产生挤出效应；另一方面，资本规模扩张以及生活成本的提高会促使资本对工业劳动和能源使用的替代。在挤出效应和要素的替代效应共同作用下，最终会促使资本流向技术先进地区，且对劳动力和能源产生一定程度的挤出效应。

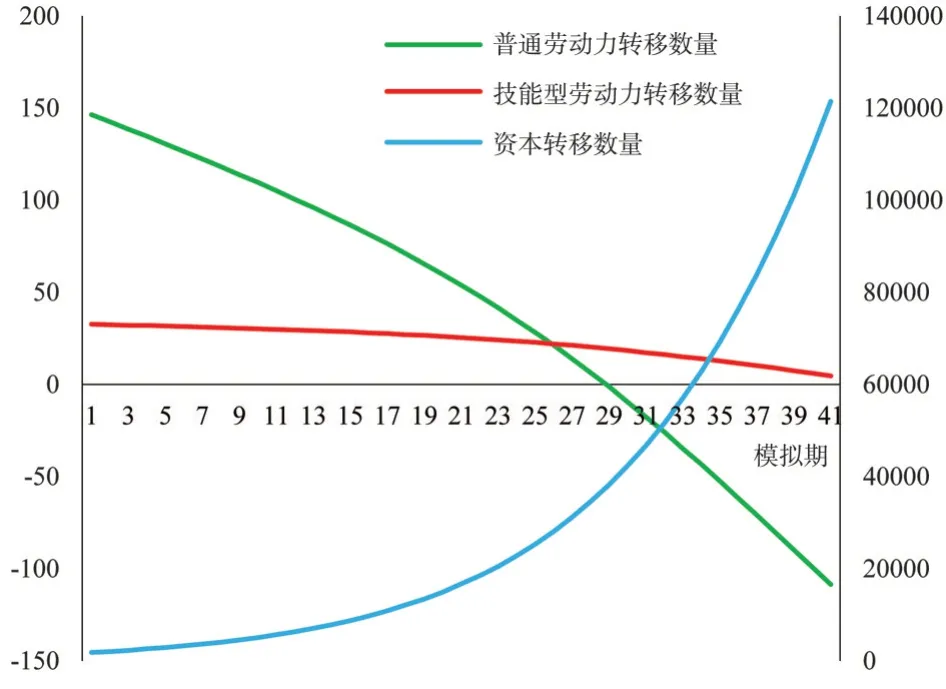
图3 地区要素流动特征

其次，在对地区产业结构的模拟中发现地区间工业会向技术要素集聚的地区迁移。具体来看，对于资本和技能型劳动力集聚的地区而言，资本的集聚会导致地区产业结构向资本密集型调整，这种特征直观地反映在流入地的工业结构上，技能型劳动力集聚和资本密集地区工业占比逐渐提高，而资本和技能型劳动力流失的地区工业占比则会因工业要素流失的双重叠加而产生萎缩。要素流失地区只能通过简单扩大生产规模来阻滞实体经济的萎缩，并不能够通过技术进步和效率提升来实现产业升级，从要素投入视角上来看，技能型劳动力流失的地区只能通过提高能源使用和简单要素投入来维持工业份额，此举不仅不利于工业升级，同时也会造成碳排放水平提高。

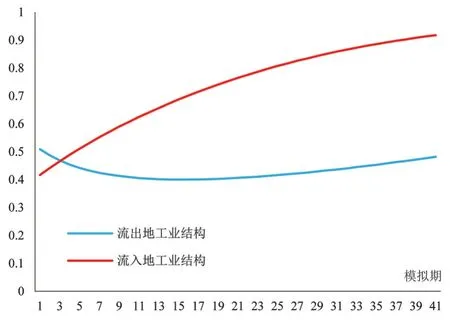
图4 地区产业结构

图5 地区劳动技能结构

图6 地区劳均资本存量（万元/人）

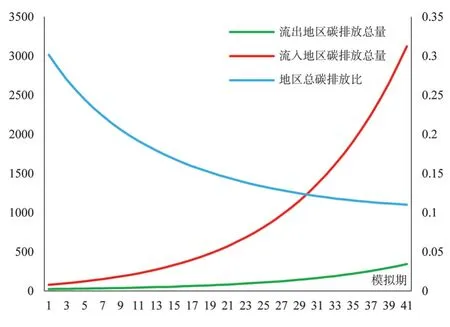
图7 地区碳排放总量（亿吨）

第三，本文模拟了地区间劳动力技能结构和地区间劳动力资本配置结构。模拟结果表明：对于流入地而言，在工业劳动力集聚的早期，因地区间产业相依性引致的服务业劳动力流动规模会快于工业劳动力的流动规模，并在一定程度上降低地区劳动力平均技能水平。因此在模拟初期发现流入地区劳动力技能结构存在微弱的下降趋势。而伴随着简单劳动力逐渐集聚并形成规模，则会导致技术集聚地区的劳动力技能结构持续提高。与之对应的是地区间劳动力的资本配置状况。由于资本对地区间利率差异的敏感性要显著高于劳动力对地区间工资差异的敏感性，因此资本流动规模的变动速度会显著快于劳动力流动规模的变动速度，这就导致了地区间劳均资本存量显著提高，资本深化促使了地区间工业集聚。

最后，本文模拟了地区碳排放总量和地区劳均碳排放量的演化路径。从碳排放总量上来看，由于流入地在经济体量上和流出地存在一定差距，因此流入地碳排放总量较流出地而言存在一定差距。但从相对变化来看，伴随着流入地技能型劳动力集聚和技术进步，流入地区的碳排放总量增长趋势较流出地而言更加缓慢，地区碳排放比呈现出下降的趋势。这表明要素集聚，尤其是技能型劳动力的集聚会对地区化石能源使用存在一定程度的替代，技术进步会提高化石能源的利用效率，进而促进技术进步和碳减排同时发生。

上述结论在劳均碳排放这一指标的演化趋势上更加显著。从图8看出，无论是对于劳动力流入地，还是对于劳动力流出地而言，地区劳均碳排放量均呈现下降的趋势。对要素流出地而言，要素流失造成地区行业规模收缩，不仅减少了能源的使用，同时在碳减排政策的影响下，厂商和行业出于成本最小化原则，会利用其他要素对能源进行替代，进而导致能源使用量降低的程度要大于劳动力流失的程度，造成流出地劳均碳排放下降。对于流入地而言，一方面劳动力集聚会促使能源利用效率的提高，另一方面技能型劳动力及其引致的资本会对能源产生更大程度的替代，综合表现为流入地劳均碳排放呈现下降的趋势，且较流出地而言，碳减排程度和效果更好。

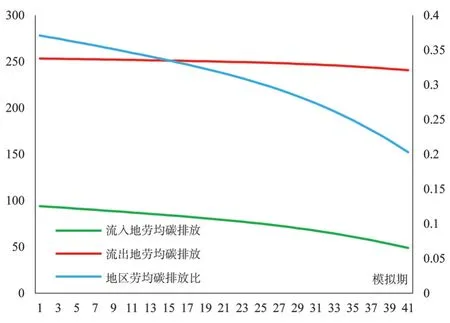
图8 地区劳均碳排放量（千吨/万人）

四、异质性劳动力流动与地区碳排放的实证检验

1.变量构造及数据选取

上文理论方程的建立以及数值模拟的结果显示：地区间异质性劳动力流动（尤其是技能型劳动力的流动）对地区间要素相对配置和产业结构调整存在显著影响。由此，揭示异质性劳动力流动对地区碳排放之间的关系，本质上在于检验技能型劳动力流动是否能够促进地区间技术进步和能源利用效率的提高以及人力资本和物质资本对能源的替代。因此，本文利用空间计量的方法对理论模型揭示的异质性要素配置的内生机制以及数值模拟推演的关键结论进行实证检验。

本文核心被解释变量为碳排放，选取地区CO2排放总量（千吨）作为相应的度量指标。关于核心解释变量的选取，针对理论模型的关键结论，以“地区年末常住人口”与“地区年末户籍人口”之间的差，比上“地区年末户籍人口”，作为劳动力净迁入比率（migit）；［5］［30］选取地区本科及以上学历劳动力数量作为衡量技能型劳动力的指标（skillit）；选取城镇单位就业人员总量、私营企业就业人员和个体就业人员总量（万人），并扣除技能型劳动力作为衡量地区劳动力数量的指标（labit）；选取工业增加值占GDP份额作为产业结构（struit）的代理指标；选取化石能源使用量占能源总使用量的份额作为能源结构（feit）的代理指标。

考虑数据完整性，本文所采用的指标横跨的时间序列为2004-2019 年。其中，碳排放数据源于Wind数据库；化石能源使用量相应数据源于《中国能源统计年鉴》；工业增加值和GDP数据在具体实证过程中均经过价格平减，相应数据源于《中经网统计数据库》；技能型劳动力数据源于《中国人口和就业统计年鉴》。详细的指标含义、处理过程见表1。

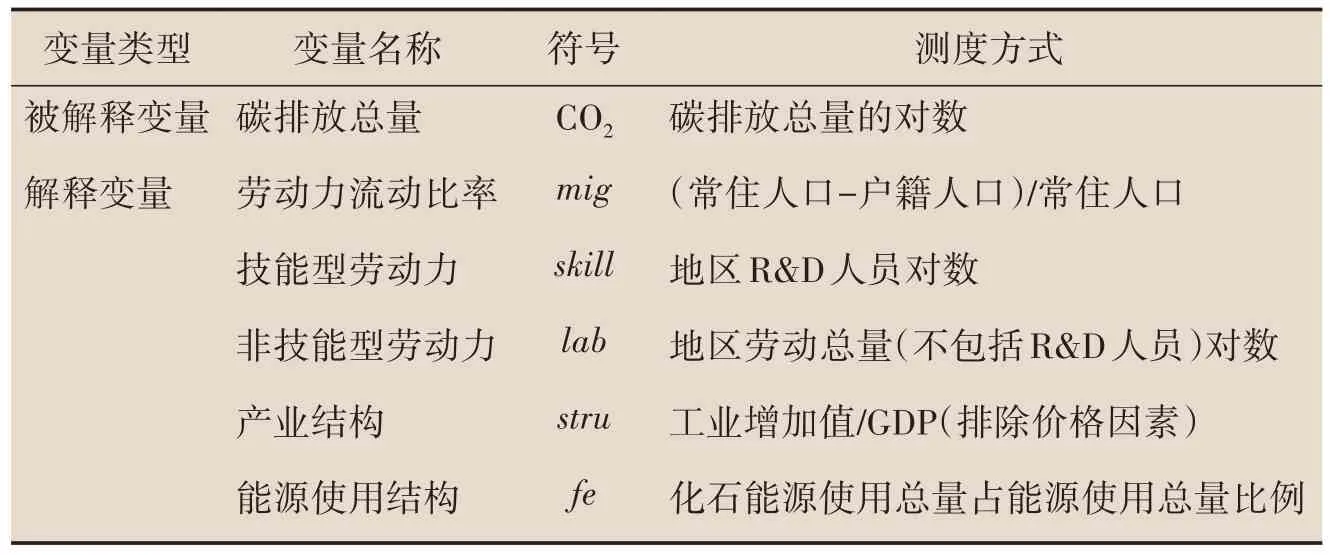
表1 主要变量定义及测量方式

2.空间相关性检验

尽管前文理论模型从机制上识别出了技能型劳动力流动导致的能源利用效率提高以及要素配置状态的改变。但在异质性劳动力流动过程中技术是否存在溢出效应以及不同地区技能型劳动力技术溢出效应是否相同是决定各地区碳排放向特定水平收敛的关键。因此，在以空间计量手段检验异质性劳动力跨区域流动与地区碳排放之间关系的过程中，首先要解决的问题是检验各个地区是否存在空间性。对此，采用经典的空间相关莫兰指数对地区间可能存在的空间相关性进行验证：

其中，S2=，xi为第i个地区的观测值，在本文中xi具体代表该地区的人均CO2排放水平，n为地区总数；wij为空间矩阵W中的元素。莫兰指数的取值范围为［-1，1］，数值越大表示地区间的空间正相关性越强；数值越小则表示地区间负相关性越强；当莫兰指数接近0值时，表明地区间不存在显著的空间相关性。本文选用经济距离矩阵计算莫兰指数，在后续的实证检验过程中也将经济距离矩阵作为主要的空间权重矩阵紧缩实证检验，并通过替换不同的空间权重矩阵作为稳健性检验的方式。全局自相关莫兰指数的具体计算结果见表2。

表2 莫兰指数时间变化趋势

根据计算的全局莫兰指数结果，从时间趋势来看，全国范围内的空间相关性逐渐减弱，显著性也逐渐减弱。同时一个有趣的现象是计算所得的莫兰指数均为正值，表明相邻地区之间表现出较为一致的碳排放特征，空间邻近的省份或地区的碳排放结构类似。为进一步揭示不同地区的碳排放结构和劳动力流动特征，本文采取LISA分析的方式来描述不同地区劳动力和碳排放的集聚特征①具体的结果染色图可向作者索要。。

从各省劳动力的地理分布来看，表现出显著的High-High 集聚特征的俱乐部仍然为位于东南沿海地区的江苏，位于珠三角地区的广东，以及西部的中心地区四川、重庆；而表现出明显虹吸效应的High-Low 集聚特征的地区主要为北京、上海和西安，这三个地区劳动力数量的增加并未对周围地区形成有明显的技术溢出，也未与周围地区形成积极的知识交流；此外，大部分中部地区与东部地区之间存在显著的负向空间自相关，表现出显著的Low-High 集聚特征；最后，大部分西部地区仍然表现出劳动力数量低水平的Low-Low集聚特征。而从时间变动趋势来看，劳动力的流动逐渐向发达地区集中，即劳动力逐渐向东南沿海地区、北京地区和川渝地区集中，而中部地区并未与东部地区形成较好的知识交流，表现出显著的负向空间自相关，此外西部地区的劳动力密度则更加稀疏。这些时间特征均表明劳动力，尤其是技能型劳动力，逐渐在技术优势地区形成了集聚效应。

从各省碳排放的地理分布来看，各省的碳排放水平仍然在珠三角、长三角地区形成了较强的空间关联，表现出明显的High-High 集聚特征；北京地区的高技能劳动力对周边地区存在显著的虹吸效应，表现为显著的High-Low 集聚特征；中部地区的碳排放水平仍然表现出本地水平较低、周边水平较高的Low-High 的空间负相关集聚特征；绝大部分西部地区表现出显著的低水平的俱乐部集聚现象。从时间趋势上来看，全国范围内碳排放水平逐渐集聚于东南沿海地区和北京地区，中、西部地区的碳排放水平逐渐减少且未与周边地区形成较强的空间联动。

将上述结果与图1 和图2 所显示的规律对比，发现目前劳动力和碳排放的空间集聚特征极为相似。劳动力集聚和城市碳排放集聚之间存在较强的耦合关系。这初步表明地区产业结构（高碳排放的工业）会随着劳动力的集聚而集聚。在地区工业扩大生产规模过程中，劳动力流动和劳动力集聚对地区能源集聚存在显著的引致效应。而技能型劳动力集聚是否会反向推动能源利用技术升级，本文进一步采取空间计量的手段对此进行验证。

3.碳排放与劳动力流动的实证检验

结合上文的理论模型可以看出，一方面，技能型劳动力的集聚程度会促使地区资本深化，并促进地区产业结构向资本密集型产业调整，推动地区现代产业（工业）集聚的发生，而地区工业集聚是造成地区碳排放水平提高的决定因素。另一方面，技能型劳动力集聚对技术进步的主要驱动因素，不仅能够替代资本和简单劳动力，同时能够反向推动能源利用技术升级，提高能源利用效率的同时降低能源消耗总量。另外，前文理论模型发现产业相依性决定了高碳排行业的发展不能脱离低碳排行业的支持，技能型劳动力集聚不仅对能源和简单劳动力存在挤出效应，同时产业相依性决定了技能型劳动力集聚对能源之间存在引致效用。最终异质性劳动力流动和碳排放之间关系取决于上述三种作用力的相对均衡。为验证理论模型的结论，本文构建如下空间杜宾面板模型（SDM）①本文首先采用LM 检验，结果表明SEM 模型、SAR 模型均适用（LM-lag 检验、R-LM-lag 检验、LM-err 检验、R-LM-err 检验均通过1%的显著性水平检验）；其次，LR 检验显著地拒绝了原假设，说明SDM 模型不会简化为SEM 模型或SEM 模型；再次，Hausman检验结果支持固定效应；最后，联合显著性检验拒绝了原假设，说明选用时间和个体双重固定的SDM模型较为合适。对此进行检验。

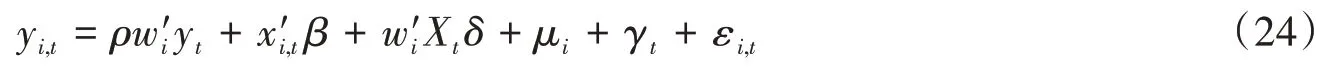
表3 地区碳排放与异质性劳动力流动的单区制空间计量检验

从上述实证结果可以看出，无论采用何种空间权重矩阵，各变量的符号均未发生系统性变化，表明本文采用空间杜宾模型所得到的回归结果是稳健可信的。就各个变量估计值所传递的具体含义来看，首先，简单劳动力总量的集聚、劳动力流动比率与地区碳排放之间存在一定的正向关系，表明地区劳动力总量增加会引致工业规模扩大，从而提高碳排放水平。类似的经济传导机制在地区产业结构（stru）、化石类能源使用比率（fe）的系数上也有体现：当地区工业规模扩张、使用化石能源比率上升，则必然增加地区碳排放水平。

地区劳动力流动比率和技能型劳动力对地区碳排放存在一定程度的负向影响，这是实证结果的一个重要发现。从前文理论机制可以判断出技能型劳动力的集聚在生产过程中不仅存在着对其他生产要素的替代，同时会反向推动能源利用技术升级，二者作用下造成技能型劳动力集聚对碳排放产生负向影响。

前文理论模型一个重要的引申结论是：生产技术水平是决定地区间产业结构、能源利用的关键，进而对碳排放存在直接影响。因此，本文采用空间计量来检验劳动力流动过程中可能存在的技术溢出效应。然而一个尚未突破的问题在于从不同地区流出的劳动力其空间溢出效应可能存在异质性，由此造成地区异质性劳动力集聚和碳排放特征也会存在差异。因此，本文采用两区制空间杜宾模型，对不同地区劳动力流动可能造成的异质性空间溢出效应进行细致区分和讨论。具体的两区制空间杜宾模型构造如下：

其中，d为虚拟变量。结合不同地区产业结构、技术水平和劳动力流动特征，本文设定北京、天津、上海、江苏、浙江、福建和广东作为区制1，其余地区作为区制2，以此揭示不同地区劳动力流动过程中可能存在的异质性空间溢出效应。具体计算结果见表4，同时表5 汇报了各变量的空间溢出效应。

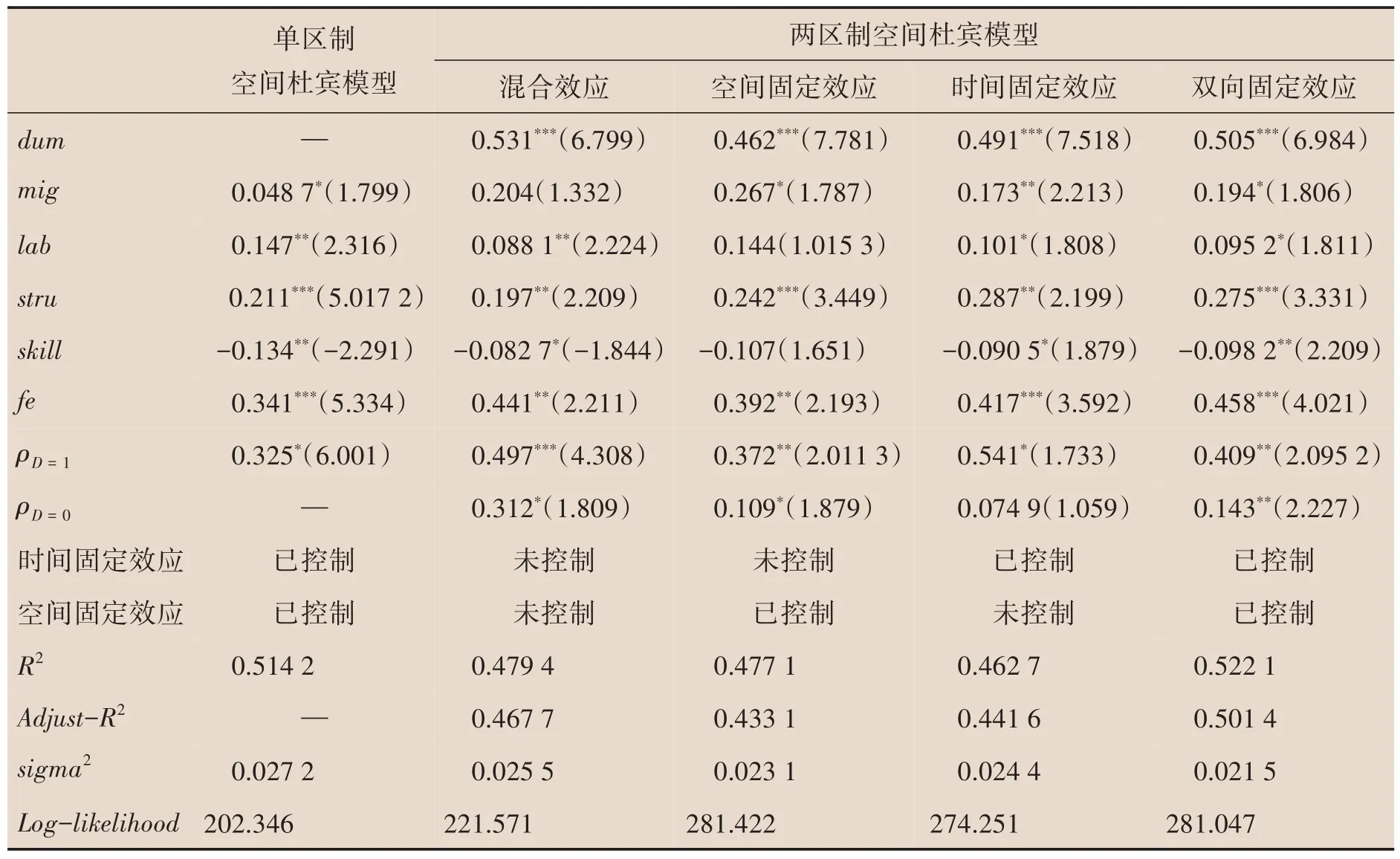
表4 地区碳排放与异质性劳动力流动的双区制空间计量检验

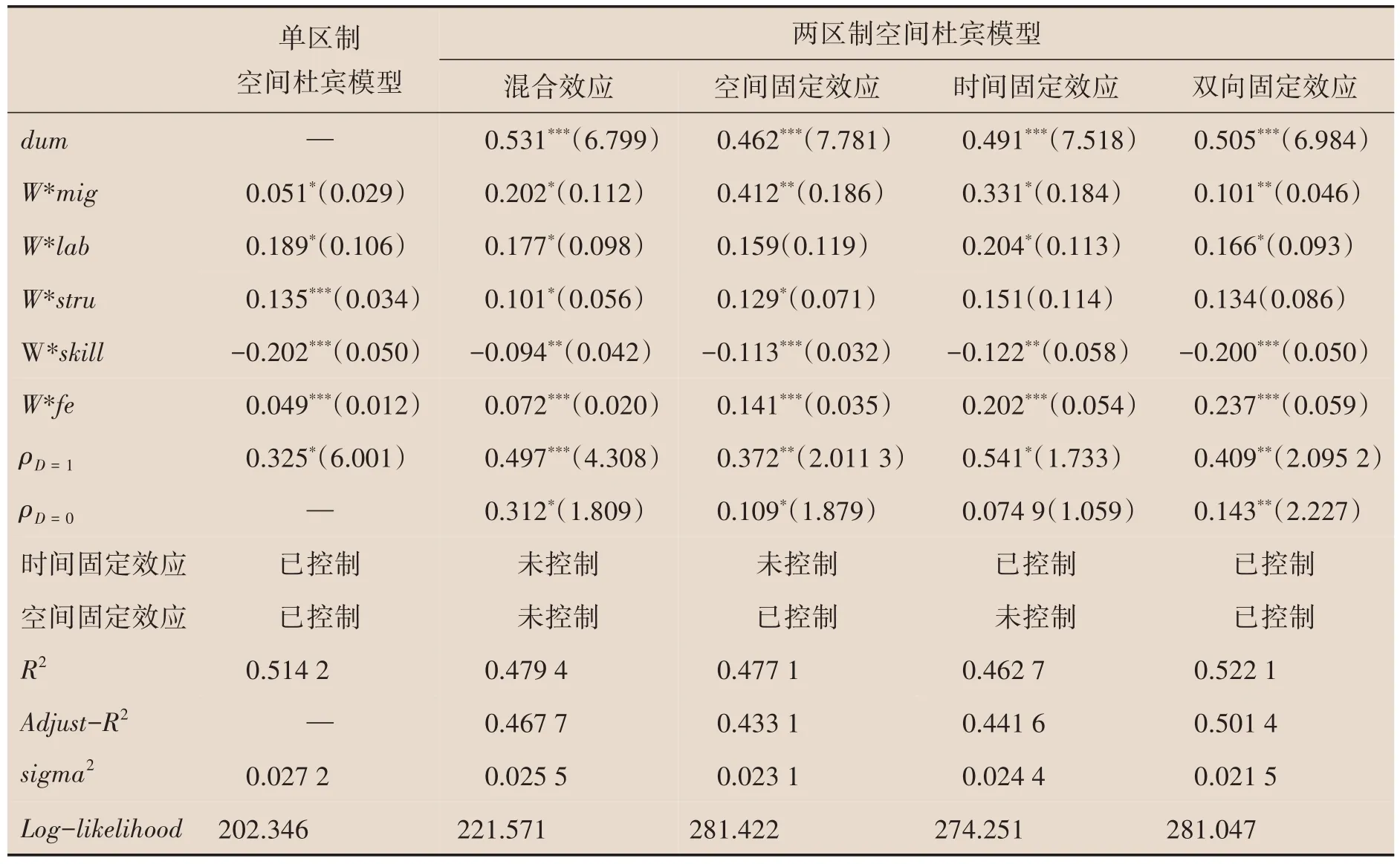
表5 地区碳排放与异质性劳动力流动的空间溢出效应

分析两区制空间杜宾模型的结果发现，整体上，两区制空间杜宾模型和单区制空间杜宾模型所表现出的经济规律是类似的：无论是表示工业生产规模的劳动力总量（lab）、劳动力流动比率（mig），抑或是代表地区工业化程度的产业结构（stru），或者是地区化石能源消耗（fe），整体而言均会对地区碳排放水平产生显著的正向影响；而技能型劳动力集聚，整体而言则会对地区碳排放产生不同显著程度的负向影响。

进一步对比不同区制所反映出的规律，发现对于技术水平较为先进、技能型劳动力集聚程度较高的地区（d=1），上述变量的影响系数要显著大于技术水平较为落后、技能型劳动力集聚程度较低的地区（d=0），尤其是对于技能型劳动力集聚程度而言。由于ρd=1·d＞ρd=0·(1-d)，当技能型劳动力向技术优势、产业结构高端的地区集聚时，较高的技术水平存量更能发挥技能型劳动力的研发效应和替代效应，因此对能源和其他要素的替代作用更强。

五、结论

本文通过构建两地区三部门的一般均衡模型，并对理论模型的关键结论进行数值模拟，从理论层面揭示了异质性劳动力流动和地区碳排放之间的内在机制。随后，本文利用我国省际宏观数据对理论模型所阐释的理论机制进行实证检验，得到如下结论：

首先，本文从理论上揭示了技能型劳动力集聚会通过提高能源利用水平，以及对能源和其他生产要素的替代，从而实现二氧化碳排放的减少。具体而言，在理论模型建立过程中，通过识别不同劳动力的异质性碳排放特征，刻画了工业劳动力与传统服务业劳动力流动过程中存在的联动机制。这种联动机制从总量上决定了地区碳排放的整体水平，从结构上决定了技能型劳动力对能源的替代程度，从而实现技术进步和碳减排。最终二者之间的均衡共同决定了地区碳排放总量。

其次，本文采用数值模拟的方式，针对理论模型揭示的异质性劳动力流动和碳排放之间的内在机制进行演化分析。从地区产业结构演变这一视角来看，技能型劳动力的集聚会带来地区产业结构高级化；从要素的配置角度来看，技能型劳动力的集聚一方面对非技能型劳动力产生了替代，另一方面对资本流动存在引致作用，二者共同作用造成了地区资本深化，进一步促使产业结构向资本密集型和技能密集型演化；由于资本密集型产业结构和技能密集型产业结构对地区碳排放的作用机制相反，从现阶段中国地区经济发展模型和碳减排的结果来看，由技能集聚反向推动能源技术进步，进而促使碳减排的效应要强于资本深化和规模扩张带来的高碳排效应，最终促使地区平均碳排放水平降低。

最后，本文对理论模型的关键结论以及数值模拟对经济演化的基本判断进行实证检验。本文分别采用单区制空间杜宾模型和双区制空间杜宾模型，对异质性劳动力流动过程中可能存在的异质性溢出效应进行甄别和检验。结果表明工业规模扩张、生产要素投入以及化石能源的使用对地区碳排放水平存在不同显著水平的正向影响，而技能型劳动力集聚则对地区碳减排存在显著影响。同时，在技能型劳动力集聚和技术水平更高的地区更容易发挥技能型劳动力对能源利用技术进步的反向推动作用，技能型劳动力的碳减排效应更强。

就本文的研究而言，有效疏导异质性劳动力的流动，在吸引技能型劳动力集聚、促进产业升级的同时，加快实现地区经济增长由传统的“要素驱动”向“研发驱动”转变，是保证经济高质量发展同时实现碳减排的有效途径；此外，能源使用结构的改变和升级是一个较长期的过程，在大力发展清洁能源的同时，应强调优化能源消费结构、促使能源利用技术创新、提高能源使用效率。最后，应充分考虑经济环境和企业生存环境，针对行业特征实施和制定异质性碳减排、碳达峰目标，并给予相应的经济补偿，确保发挥企业对经济运行的创新活力。