基于LBP和GLCM的肠道肿瘤图像特征提取方法
2022-08-04张立娜韩霄松
杨 波, 张立娜, 韩霄松
(1. 长春财经学院 信息工程学院, 长春 130122; 2. 吉林农业大学 信息技术学院, 长春 130118;3. 吉林大学 符号计算与知识工程教育部重点实验室, 长春 130012;4. 吉林大学 计算机科学与技术学院, 长春 130012)
目前针对肠癌的诊断, 医生通常采用指检和肠道镜等方式进行早期排查, 由于肠癌早期症状不明显, 给医生诊断带来巨大挑战. 通过指检和肠道镜检查, 排查早期肠癌的准确率约为80%, 一旦早期诊断出现失误, 会对癌症的及时治疗和患者心理造成极大影响. 通过对肠镜和CT图像进行实时处理, 提取图像特征辅助肠癌早期识别, 可极大提高诊断效率. 基于此, 本文提出一种基于局部二进制模式(local binary patterns, LBP) 和灰度共生矩阵(gray level co-occurrence matrix, GLCM)的肠道肿瘤图像特征提取与识别方法, 分割肠道肿瘤的病灶区域, 通过 LBP算法和 GLCM的结合, 判断肠癌和息肉差异性的同时, 确定适用于肠癌识别分类的特征参数, 进一步提高肠癌早期诊断预测的准确率.
1 肠道肿瘤图像的感兴趣区域
肠道恶性肿瘤通常呈球状或半球状凸起, 体积较大, 有的恶性肿瘤伴随出血、 底部深陷等特点, 也有多个肿瘤集中在一起出现肠腔狭窄的情况. 根据肠道肿瘤的特点, 在对图像进行特征提取和识别前, 需将肠道肿瘤区域从医学图像中进行有效分离, 从而进行更有针对性的研究.
OTSU算法, 即最大类间方差法, 是在判别分析或最小二乘原理基础上发展而来的[1], 也称为大津法. 用最大类间方差法可以得到医学图像的一个合适阈值, 利用im2bw函数将图像转换为二值图像的过程中, 通常须设置阈值, 该函数能获得一个较合适的阈值. 该阈值与人工设定阈值相比能得到更好的转换效果.
利用OTSU算法按照肿瘤图像灰度的特性, 将肿瘤图像分割成背景和前景两部分, 其中前景又称为目标. 类间方差越大, 表明图像中的背景和目标之间的差异性越大. 出现误分情况时, 即存在个别目标被误分为背景, 或个别背景被误分为目标, 会使差别变小. 因此, 类间方差最大的分割, 误分几率最小. 对于图像A(x,y), 假设目标与背景的分割阈值为T, 目标像素点数占整个图像的百分数标记为ω0, 其平均灰度为μ0, 背景像素点数占整个图像的百分数标记为ω1, 其平均灰度为μ1.该图像的总平均灰度记为μ, 类间方差记为g, 假设该肿瘤图像的尺寸为M×N, 图像中像素的灰度值小于阈值T的像素个数记为N0, 像素灰度大于阈值T的像素个数记为N1, 则有
将μ=ω0×μ0+ω1×μ1代入式(5)可得
g=ω0×ω1(μ0-μ1)2.
(6)
利用遍历求得使类间方差最大的阈值T.
用OTSU算法得出输入肿瘤图像的阈值, 计算最大和最小值, 从最小灰度值到最大值分别计算方差, 计算目标和背景的百分数和平均灰度值. OTSU算法计算前原始图像如图1所示, Graythresh函数计算阈值图像如图2所示, 简化OTSU算法计算阈值图像如图3所示.
图1 OTSU算法计算前原始图像区域Fig.1 Original image area before OTSU algorithm calculation
由图2可见, Graythresh函数计算阈值图像肿瘤区域基本被标识为白色区域, 可与背景区域有效区别. 由图3可见, 简化后OTSU算法计算阈值图像与Graythresh函数方法得到的图像效果相当. 获得肠癌肿瘤区域轮廓后, 利用drawContours( )函数绘制轮廓并进行区域剪切, 即可得到理想的肿瘤区域图像. 与计算机视觉开源框架OpenCV自带算法实验对比表明, 在分割效果上观察OTSU算法与OpenCV自带算法相当, 在计算速度上, OTSU算法时间为0.8 ms, 比OpenCV自带算法快0.2 ms.

图2 Graythresh函数计算阈值图像Fig.2 Threshold image calculated by Graythresh function

图3 简化OTSU算法计算阈值图像Fig.3 Threshold image calculated by simplified OTSU algorithm
2 肠道肿瘤图像特征提取
2.1 局部二值模式图像特征
局部二进制模式(LBP)算法一般将一张图像划分为中心区和邻区. 如果30为中心区的像素灰度值, 则将其作为阈值, 此时把图像中心区获得的像素值与相邻8个区获得的像素值对比[2]. 假设该图像的中心区获取像素值大于对比邻区像素值, 则邻区可以将对应位置的像素值设定为1, 否则如果邻区像素值大于中心区值, 则将邻区对应位置记为0. 以此类推, 将整个标记完的区域从左上角按照顺时针读取8个二进制数, 形成一个二值化后的序列, 其对应的十进制数作为该邻域中心点的响应. 基本LBP算子的获取过程如图4所示.
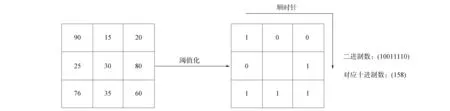
图4 基本LBP算子的获取过程Fig.4 Acquisition process of basic LBP operators
LBP算法局部纹理特征计算公式[3]为
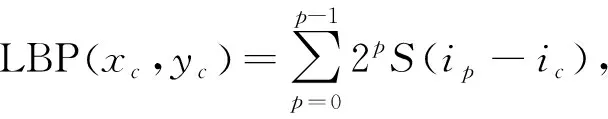
(7)
其中: (xc,yc)为图像的中心区像素坐标;p为8邻区中的第p个像素点;ip为p点对应的灰度值;ic为中心区像素对应的灰度值;S(x)为符号函数,
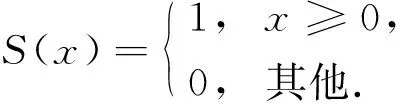
(8)
本文通过实验将肠道肿瘤图像的各像素点均通过LBP计算, 获得的新肿瘤图像与原肿瘤图像大小相同, 称为LBP图像. 同时计算并绘制肿瘤LBP 图像的直方图, 作为描述肿瘤图像纹理特征的辅助方式[4]. 但基本的LBP算子计算得到的直方图会出现维数较多的情况, 利用图像等价模式LBP特征在一定程度上可达到降维的效果.
本文采用LBP算法获取图像原始LBP特征, 并显示其统计直方图与特征图像, 肿瘤特征被有效保存, 单肿瘤图像特征效果如图5和图6所示, 多肿瘤图像特征效果如图7和图8所示.
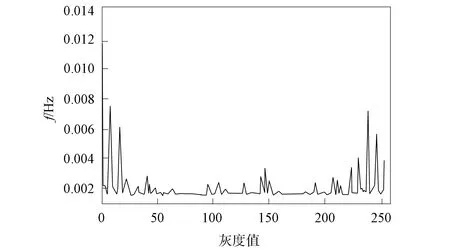
图5 单肿瘤图像统计直方图Fig.5 Statistical histogram of single tumor image

图6 单肿瘤图像LBP特征图Fig.6 LBP characteristic map of single tumor image
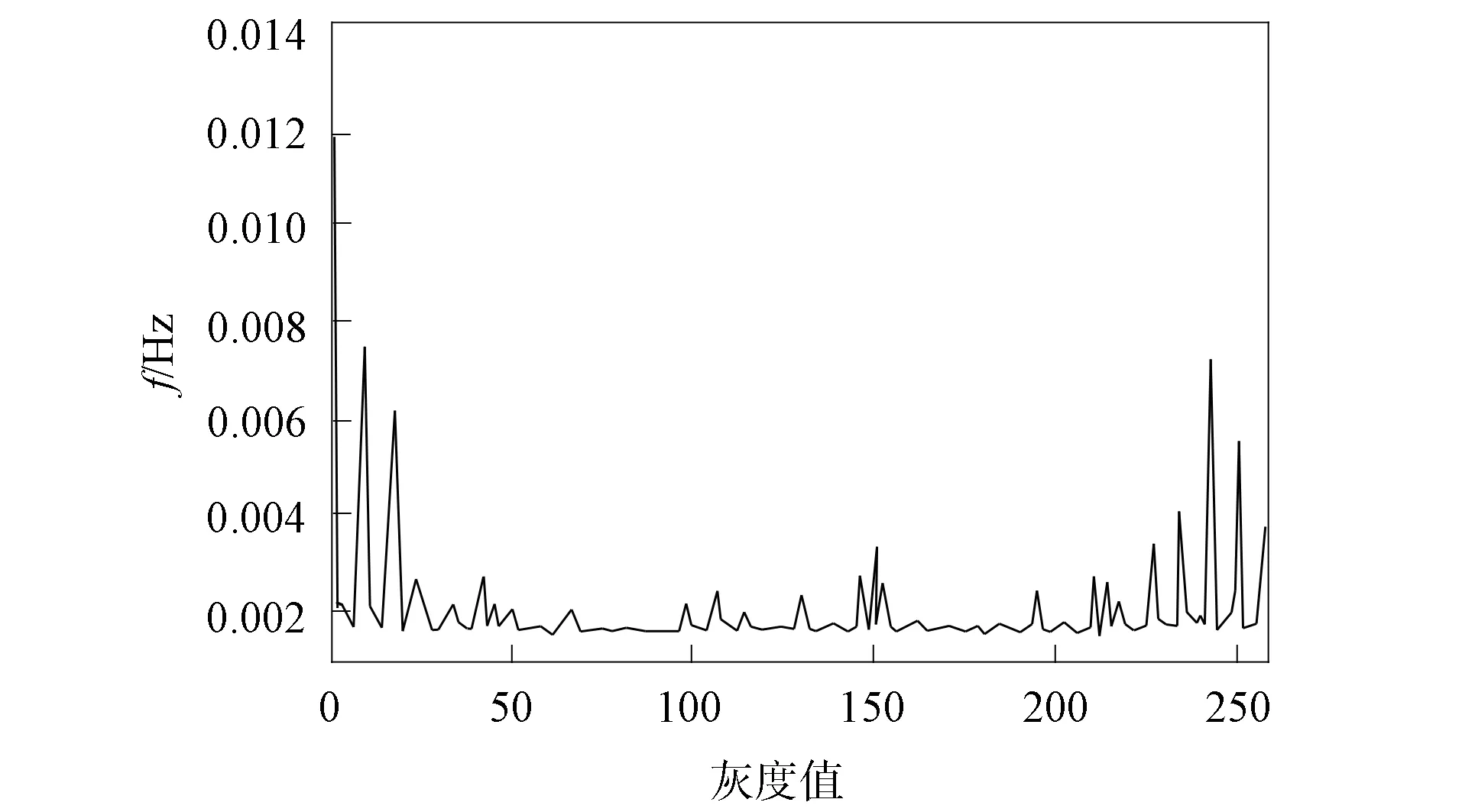
图7 多肿瘤图像统计直方图Fig.7 Statistical histogram of multiple tumor image

图8 多肿瘤图像LBP特征图Fig.8 LBP characteristic map of multiple tumor image
图9为图像等价模式直方图, 图10为图像等价模式LBP特征图. 由图9和图10可见, 采用图像等价模式LBP能表示大多数纹理特征, 同时处理速度得到显著提高, 有效特征也可以得到较好的保留.
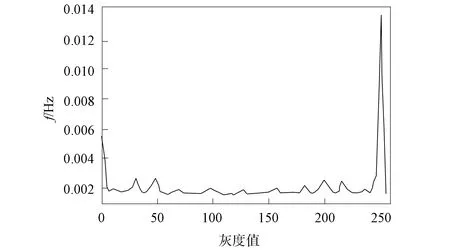
图9 图像等价模式统计直方图Fig.9 Statistical histogram of image equivalent pattern

图10 图像等价模式LBP特征图Fig.10 LBP characteristic map of image equivalent pattern
2.2 灰度共生矩阵
灰度共生矩阵(GLCM)计算两个点在一定距离和一定方向上的灰度相关性, GLCM反映了图像在方向、 间隔、 变化范围和速度等方面的综合信息[5]. 本文利用GLCM进行全局纹理特征提取, 设肿瘤数字图像尺寸为M×N, 灰度为K, 为定义肿瘤图像任意一对像素作为条件的概率密度, 假设预先给定距离d和方向θ(θ为像素对点之间连线与坐标的夹角), 灰度以i为起点, 出现灰度为j的概率.即GLCM是指目标图像中满足d和θ成对点灰度出现率, 此概率用P(i,j,d,θ)表示:
P(i,j,d,θ)=([(x,y),(x+m,y+n)|f(x,y)=i,f(x+m,y+n)=j]),
(9)
实际上是(K×K)的矩阵. 图11为GLCM算法示意图. 图11中灰度为i的点坐标为(x,y), 灰度为j的点是偏离灰度为i的另一点, 坐标为(x+m,y+n), (m,n)为偏离值, 则此时将GLCM中相应位置(x,y)处的值加1(初始值为0)[6].
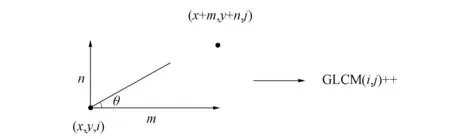
图11 GLCM算法示意图Fig.11 Schematic diagram of GLCM algorithm
在实际应用中, GLCM通常不能直接区分纹理特征, 需要一些属性作为纹理特征的描述, 其中包括14种基于灰度共生矩阵计算出的统计量[7]: 能量(角二阶矩)、 熵、 对比度、 均匀性、 相关性、 方差、 和平均、 和方差、 和熵、 差方差、 差平均、 差熵、 相关信息测度以及最大相关系数[8]. 根据需要和实际应用效果, 本文采用角二阶矩、 熵、 对比度和反差分矩阵4个统计量. 4个统计量计算方法为
其中: 角二阶矩ASM表示肿瘤图像的灰度分布均匀水平和纹理粗细程度,P(i,j)表示归一化后的灰度共生矩阵; 熵ENT表示肿瘤图像包含信息量的随机性, 同时也反映肿瘤图像的复杂程度; 对比度CON表示图像清晰度和肿瘤纹理沟纹深度, 纹理越明显, 肿瘤图像中的明暗差距越大; 反差分矩阵IDM又称为逆方差, 表示肿瘤图像纹理的清晰水平和规则程度, 该值越大, 表示纹理越清晰[9], 同时越有规律性. 以单个肿瘤为例, GLCM结果如图12所示.

图12 GLCM结果Fig.12 GLCM results
将包含单个肿瘤、 多肿瘤和无肿瘤图像的LBP图, 根据式(10)~(13)计算获取GLCM特征值, 对比结果列于表1. 表1中特征值均为单一样本特征数据. 由表1可见, 多肿瘤图像的GLCM角二阶矩值相对较大, 表示纹理容易描述, GLCM的熵值反映肿瘤图像相对复杂[10], 对比度较大说明多肿瘤图像纹理较清晰, 更容易识别.

表1 GLCM肿瘤特征值对比
实际使用过程中, 根据肠道肿瘤医学图像的纹理特征, 采用4个方向(0°,45°,90°,135°)生成灰度共生矩阵, 每个方向使用4个统计量标识特征, 生成16个特征值. 再通过计算4个统计量的均值、 标准差和方差, 生成12个特征值, 共28个特征值描述一个肠道肿瘤图像, 产生的矩阵部分数据列于表2.
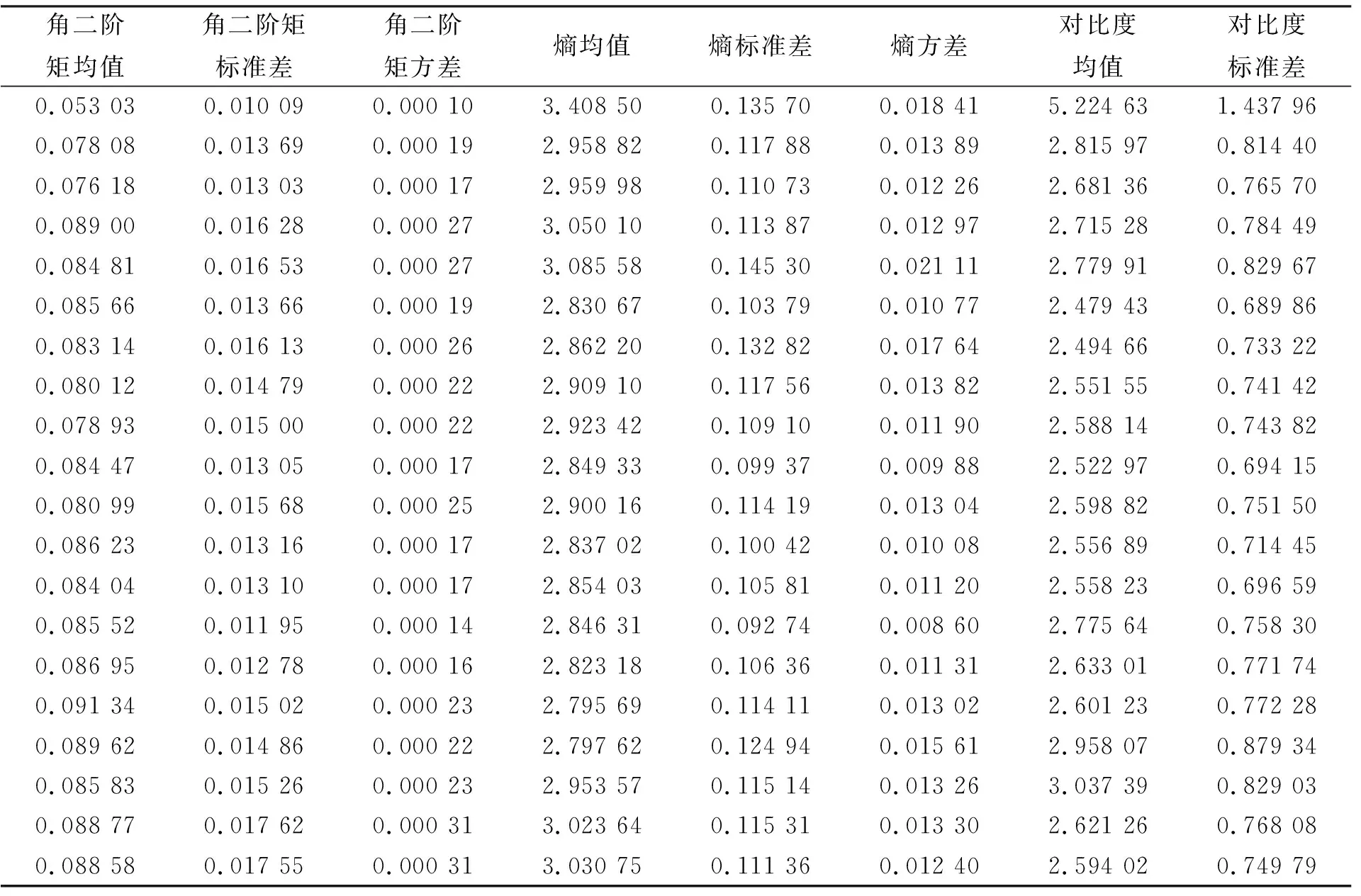
表2 肠道肿瘤图像GLCM特征
3 实验结果与分析
本文采用的实验数据为吉林大学第一医院二部肠镜检查数据图像, 来自200名患病个体, 图像信息1 500个. 实验图像数据需要临床医师进行标定, 肠镜样本数据分为单肿瘤、 多肿瘤、 正常肠道和息肉. 临床医师根据病例结果对1 500张图像逐一标定, 最终确定实验使用的数据集. 其中700张图像作为训练数据集, 600张图像作为测试数据集, 200张图像作为待测数据集.
支持向量机(support vector machine, SVM)可以在有限样本信息的情况下, 对模型的复杂性和学习能力之间进行折衷, 获得较好的推广能力和识别效果[11]. 针对SVM识别方法, 本文采用LBP+SVM,GLCM+SVM和LBP+GLCM+SVM三种方式进行分类识别. SVM可采用多种核函数, 其中参数γ和误差惩罚因子C是核函数的主要参数, 本文利用交叉对比法.
SVM通过用内积函数定义的非线性变换将输入空间变换到一个高维空间[12]. SVM核函数K(xi,xj)是输入空间和特征空间之间的映射.
多项式核函数表示为
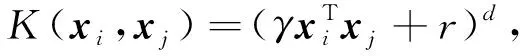
(14)
径向基核函数(RBF)表示为
K(xi,xj)=exp{-γ‖xi-xj‖2},
(15)
其中d为多项式次数,γ为模型复杂度系数. 通过核函数的使用, SVM将二维线性不可分样本映射到高维空间中[13]. 样本数据在高维空间中变得线性可分.
针对肠道肿瘤样本数据, 本文测试了SVM两种核函数的识别准确率, 结果表明, 多项式函数当多项式次数达到一定值时精度开始下降, 次数D=4时达到最高.RBF核函数精度普遍高于多项式函数, 当C=26,γ=0.3时, 精度达到最高. 本文选择深度学习的VGG模型作为对比实验, 该模型相比传统卷积神经网络更适合样本数较少的识别任务[14]. 在样本集上, VGG19模型的损失值结果如图13所示, 准确率结果如图14所示. 不同方法实验对比结果列于表3.

图13 样本集上VGG19的损失值Fig.13 Loss values of VGG19 on sample set
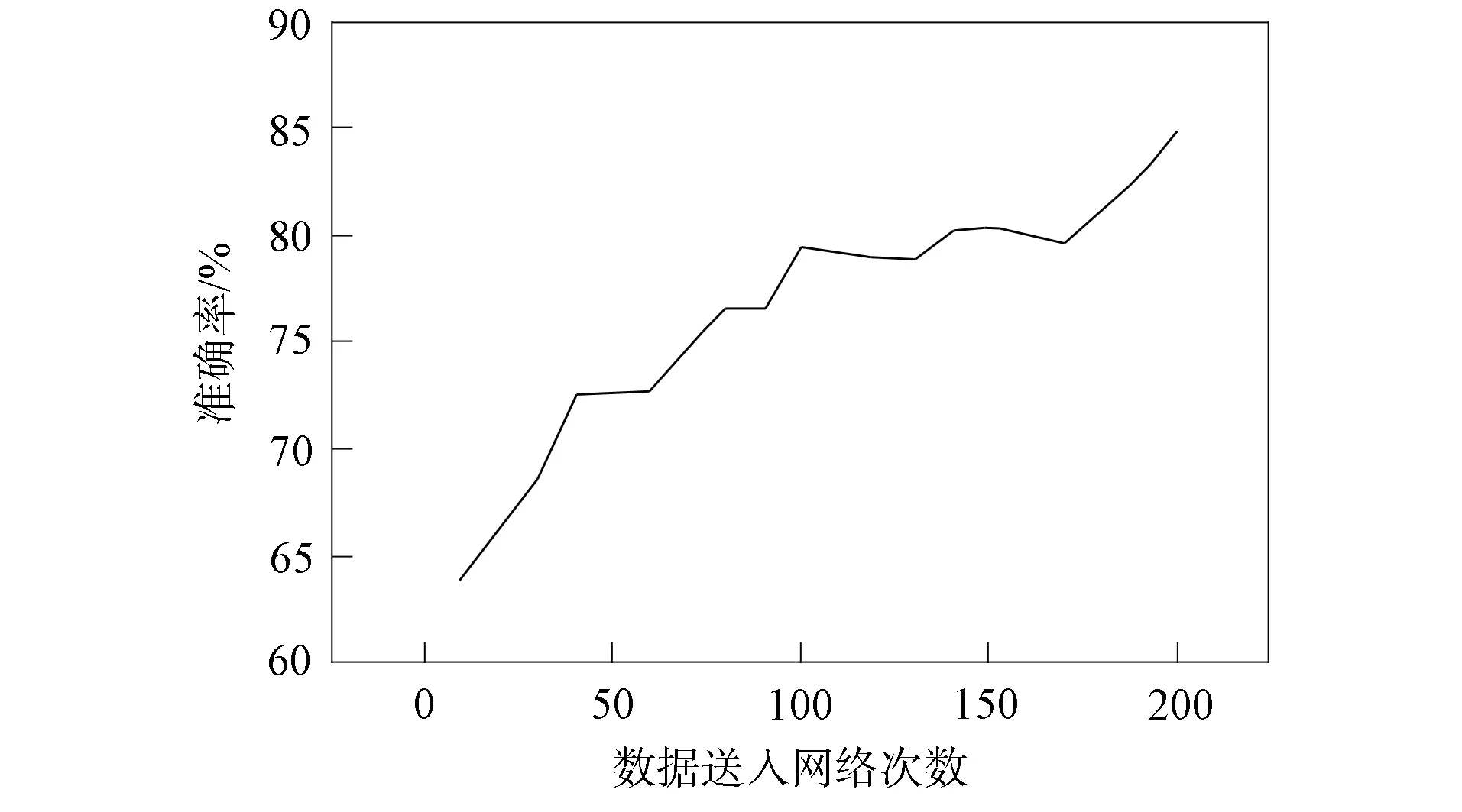
图14 样本集上VGG19的验证准确率Fig.14 Verification accuracy of VGG19 on sample set

表3 不同方法的实验结果对比
由表3可见, 直接采用LBP模式图像特征提取方法对肠道肿瘤医学图像进行识别分类的准确率为85.66%, 局部纹理特征提取后进行SVM识别效果不明显. 采用GLCM获取全局纹理特征提取法识别效果稍好, 准确率提高了4%. 采用LBP+GLCM+SVM方法, 准确率达到94.84%. VGG19模型经过训练, 当损失值为0.162 4时, 损失值曲线趋于平稳, 此时准确率稳定在约84.68%, 随着epochs训练迭代次数的增加, 准确率未出现明显变化.
综上所述, 针对肠道肿瘤图像样本有限导致肿瘤识别率低和收敛速度慢的问题, 本文提出了一种LBP+GLCM+SVM方法. 利用GLCM方法对肠道肿瘤图像进行全局特征纹理获取, 弥补了LBP方法缺少中心区像素点灰度计算的缺陷, 并结合了LBP高效性和GLCM鲁棒性的优点. 深度学习VGG模型方法由于卷积神经网络在训练时, 为保证训练不被过拟合, 需要大量的训练数据, 使得VGG方法样本数量要远大于SVM方法, 且训练速度较慢. 实验结果表明, SVM方法较适用于小样本数据的情形, 同时LBP+GLCM+SVM方法分类精度为94.84%, 优于VGG19方法的84.68%, 取得了较理想的识别准确率, 可实现辅助肠道肿瘤医学诊断的目的.
