斜投影乘积交换性的一些等价刻画
2022-08-04宋显花加羊杰
宋显花, 加羊杰
(1. 青海师范大学 数学与统计学院, 西宁 810008; 2. 青海师范大学 民族师范学院, 西宁 810008)
0 引 言
斜投影(也称幂等元)是结构较简单的算子, 也是最基本的算子, 在系统识别、 系统建模、 多变元分析、 参数估计等领域应用广泛. 目前, 关于斜投影的研究已取得了丰硕的成果[1-11]. 文献[1-4]主要利用算子的值域和零空间研究了两个斜投影乘积的交换性; 文献[5-6]研究了两个斜投影的和、 差、 积等群逆的存在性及其表示形式. 受上述研究工作的启发, 本文利用两个斜投影的和、 差、 积等几种代数组合的{1}-,{1,5}-,{2,5}-逆和群逆给出两个斜投影乘积可交换的等价刻画. 斜投影的其他相关研究可参见文献[7-11].
设B(X)是复Banach空间X上有界线性算子全体构成的集合.设A∈B(X), N(A)和R(A)分别表示算子A的零空间和值域空间,B(H)是复Hilbert空间H上有界线性算子全体构成的集合.设P∈B(X), 若P2=P, 则称P是斜投影.用I(X)表示B(X)上斜投影全体构成的集合.设P∈B(H), 若P2=P=P*, 则称P是投影.用P(H)表示B(H)中投影全体构成的集合,I表示相应空间上的恒等算子.线性算子A∈B(X)的升标和降标分别定义为
asc(A)=inf{p∈: N(Ap)=N(Ap+1)}, dsc(A)=inf{p∈: R(Ap)=R(Ap+1)},
设A∈B(X), 如果存在X∈B(X)满足算子方程(1),(2),(5), 则称A是群可逆算子,X为A的群逆,A的群逆存在当且仅当ind(A)≤1.若A的群逆存在, 则唯一, 记作A#.设B(H)是复Hilbert空间H上有界线性算子全体构成的集合.设A∈B(H),A*表示算子A的伴随算子.如果存在X∈B(H)满足算子方程(1)~(4), 则称A是Moore-Penrose可逆算子,X为A的Moore-Penrose逆.A的Moore-Penrose逆存在当且仅当A的值域是闭的.若A的Moore-Penrose逆存在, 则唯一, 记作A†.对于集合K⊂{1,2,3,4,5}, 如果X∈B(X)或X∈B(H)满足方程(j)(∀j∈K), 则称X是A的K-逆,A的K-逆不一定唯一,A的所有{i,j,…,k}-逆的集合记作A{i,j,…,k}, 其中i,j,…,k∈{1,2,3,4,5}.
1 主要结果
设P,Q∈I(X), 按空间分解X=R(P)N(P), 设

(6)
由Q2=Q知

(7)
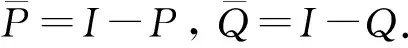
设P,Q∈I(X)如式(6)所示.由
容易验证

(12)
首先, 借助两个斜投影和的{1,5}-逆刻画两个斜投影乘积的交换性.由文献[3] 有
定理1设P,Q∈I(X), 若P+Q的{1,5}-逆存在, 则
其中(P+Q){1,5}表示算子P+Q所有{1,5}-逆的全体之集.

(13)
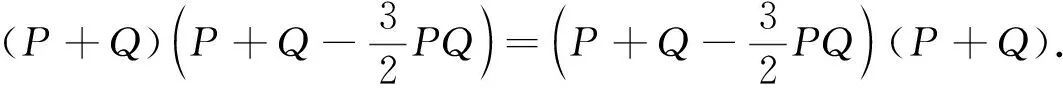
(14)
由式(6),(7)知,
从而由式(8)~(12)知
交换P,Q的位置可得
证毕.
定理1借助P+Q的{1,5}-逆给出了P,Q乘积可交换的充要条件.
注1注意到
因此, 定理1中的{1,5}-逆改成{2,5}-逆时, 结论也成立.



注3若I-PQ的{1,5}-逆存在, 则用与定理1相同的方法可证明PQ=QP⟺I-QP∈(I-PQ){1,5}.
特别地, 当P,Q∈P(H)时, 有PQ=QP⟺PQ∈P(H).于是
定理2若P,Q∈P(H), 则下列条件等价:
1)PQ=QP;
2)P-Q-PQ∈(P-Q){1};
5)I-QP∈(I-PQ){1};
6)P+Q-QP∈(P+Q-PQ){1}.
证明: 1)和2)的等价性由文献[3]中定理4.2可得.由{1}-逆的定义可知,
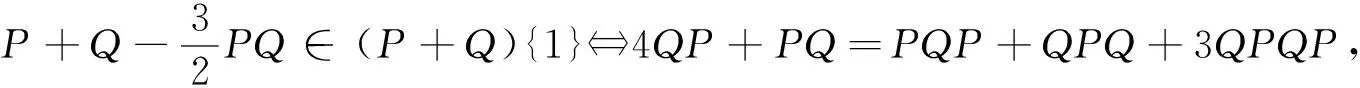
(15)

(16)
I-QP∈(I-PQ){1}⟺P+Q-QP∈(P+Q-PQ){1}⟺PQP+QPQ=PQ+QP.
(17)
将式(15)右乘P可得
QP=QPQP,
(18)
将式(16)左乘P可得
PQPQPQ+PQPQP=PQ+PQP,
(19)
将式(19)右乘Q可得
2PQPQPQ=PQ+PQPQ,
(20)
由式(19),(20)可得
PQPQ+2PQPQP=PQ+2PQP,
(21)
将式(21)右乘P可得
PQPQP=PQP,
(22)
将式(17)左乘P可得
PQ=PQPQ.
(23)
显然, 式(18),(22),(23)相互等价, 且都等价于PQ=QP.反之, 若PQ=QP, 则式(15)~(17)显然成立.于是1),3),4),5)和6)等价.证毕.
其次, 借助两个斜投影差的群逆刻画两个斜投影乘积的交换性.

此时有
设F=P(P-Q)#,G=(P-Q)#P,H=(P-Q)#(P-Q), 则F,G,H都是斜投影.
定理3设P,Q∈I(X), 若(P-Q)#存在, 则下列条件等价:
1)PQ=QP;
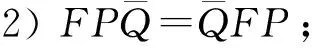
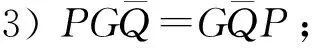
4)QHP=PQH.
证明: 由式(6)和引理1得

(24)
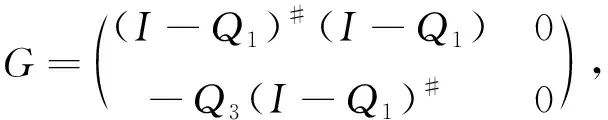
(25)

(26)
再由式(6)及式(24)~(26)知
于是

定理3利用F,G,H这3个斜投影刻画了P,Q乘积的交换性.
最后, 借助两个斜投影乘积的群逆刻画斜投影乘积的交换性.

此时

(27)

(28)

(29)

(30)
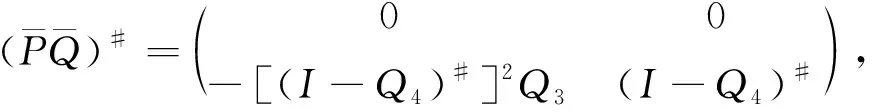
(31)

(32)

证明: 首先, 证明若(PQ)#,(QP)#存在, 则
设P,Q∈I(X)如式(6)所示, 由式(10),(11)知, 只需证明
(PQ)#=Q(QP)#⟺Q1Q2=Q2Q3=Q3Q1=0.
事实上, 有
下面证明式(33)成立⟺Q1Q2=Q2Q3=Q3Q1=0.

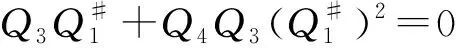
Q2Q3Q1=Q2(Q3Q1+Q4Q3)Q1=0.
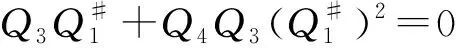
由式(12)知结论成立.证毕.

证明: 只需证明若(PQ)#存在, 则

(34)
设P,Q如式(6)所示, 由式(6),(11),(27)知


(35)


(36)
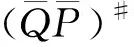
于是由式(12)知结论成立.证毕.
