基于分布式温度传感的在线学习自适应模糊温度预测法

李宁，尚雯珂

（西安交通大学电气工程学院，陕西 西安 712046）

拉曼分布式光纤传感器能够沿光纤沿线测量温度，基于拉曼散射的分布式光纤传感器已成为被广泛采用的可以监测各种结构温度状况的一种有前景的技术。但是，系统在火灾等温度突变事故中还无法快速有效实现对安全隐患的超前预警，系统的温度响应时间受到了温度传递滞后和单次解调过程的影响，只能在温度异常时实施维护机制，若想要尽早发现问题，从源头上对安全隐患采取预防措施，仍是一道技术难题。因此大量研究人员正致力于在不影响温度预测精度的前提下提高预警时间的研究。

为了实现对火灾等安全隐患的预测报警功能，研究人员提出了各种方案，例如：阈值预警方法[1]，温差预警方法，可视化定位技术[2]，模糊温差阈值法（FTDTM）[3]，离散系数预测温度算法[4]，基于多阶实时移动平均法的预警模型[1]等。在这些方法中，阈值预警和温差预警的速度主要依赖于高速采集卡的采集速率和解调运行时间，对系统硬件要求较高[4]，不经济，无法做到安全准确和防患于未然。模糊温差阈值法和离散系数预测温度算法预测的准确性还有待提高。基于多阶实时移动平均法的预警模型虽然预测温度的平均绝对误差达到了0．31℃，但在不同应用场景下需要建立不同的预警模型，使用时不方便，增加了工作量。因此在工业应用中，急需结构简单、成本较低、预测准确的超前预警系统。

本文提出了一种基于在线学习的自适应模糊温度预测方法（Adaptive Fuzzy Temperature Prediction Method Based on Online Learning，AFTPM），该预警方法对系统硬件没有特别要求，超前预警时间可以根据需求自由设定，测量准确度较高。该方法在模糊算法的基础上通过设定适当的论域实现自适应，并不断将实时数据存入历史数据中进行在线学习，实时更新训练数据，有效预测温度趋势。结果表明系统的平均预测温度的绝对误差为1．1℃，平均预测误差百分率为3．06%，预测误差的波动范围约为±2．3℃。因此本文对预防火灾的应用具有一定的理论指导作用。

1 原理

为了优化拉曼分布式光纤传感系统在实际应用中针对火灾等环境温度突变的反应速度，提高系统预警响应时间，实现超前预警，本文提出了基于在线学习的自适应模糊温度预测法。常用的预警方法是通过自定义固定阈值温度Th和计算温差阈值Td来实现报警功能，但是在实际远距离检测中，希望在火灾安全隐患发生之前能够超前预警，而传统的方法只能在温度异常时实施维护机制，并不能保证从源头解除隐患，因此面向火灾安全监控领域进行超前预警报警的难题亟待解决。

为了打破系统因传感光缆温度传递滞后效应带来温度响应时间的限制，参考了文献[3，5－10]的模糊算法，本文提出了一种基于在线学习的自适应模糊温度超前预测法。这是一种可以提前准确预测温度趋势的有效预警方法，在模糊算法的基础上通过设定适当的论域实现自适应，并不断将实时数据叠加到历史数据中进行在线学习，实时更新训练数据，能够有效预测温度趋势。

RDTS（Raman Distributed Temperature Sensor，RDTS）实验装置框图如图1所示。该系统硬件设备包括高速脉冲激光调制器（中心波长1550nm），波分复用器（波长1450nm、1550nm、1660nm），多模光纤（芯径62．5／125μm），雪崩光电二极管（带宽100MHz），高速数据采集卡（采样频率100MSa／S）。

图1 RDTS实验装置框图

当RDTS系统运行时，该系统由光发射模块输出一个10ns的光脉冲，其采用温度控制，光学性能稳定。光信号进入波分复用器后耦合到被测光纤，产生后向斯托克斯光信号和反斯托克斯光信号，后向散射光通过1660nm和1450nm两个通道分成两路分别进入光电探测器进行光电转换和放大，最后通过采集卡采集信号，并由上位机读取两路数据解调出温度。

1．1 温度解调原理

当中心波长为1550nm的光脉冲入射到被测光纤时，光纤中的脉冲光和光学声子由于非弹性碰撞发生能量转移，产生自发拉曼散射（Spontaneous Raman Scattering，SpRS）。由于激光脉冲和晶格振动模式的相互作用，处于低能级的光纤分子吸收入射光子能量，进入虚能级状态。由于光纤分子在虚能级状态极其不稳定，会从虚能级状态向高能级跃迁，过程中会释放一个光学声子，同时产生一个低频的光子，即斯托克斯光子。而处在虚能级状态的光纤分子也会向低能级跃迁，过程中会吸收一个声子，同时释放出一个高频的光子，即反斯托克斯光子。因为晶格振动受环境温度的影响[1]，SpRS的强度对光纤温度敏感。通常选择对温度敏感的反斯托克斯光作为传感信号，而选择对温度不敏感的斯托克斯光作为参考信号，这样能消除光纤在受到除温度外的其他因素干扰时引起的温度测量误差的影响。

温度T下的反斯托克斯光强与斯托克斯光强之比的表达式Fas－s（T）为：

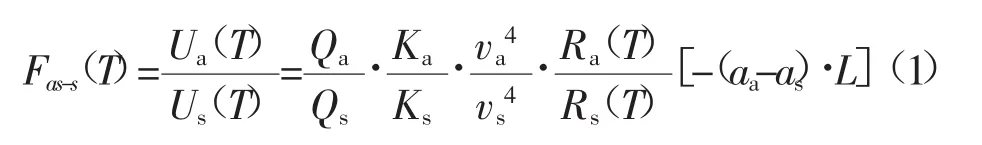
其中：Ra（T）和Rs（T）为反斯托克斯光和斯托克斯光的温度调制函数；Ua（T）和Us（T）为反斯托克斯光和斯托克斯光的输出电压；Qa和Qs为光电响应系数；Ka和Ks为反斯托克斯光和斯托克斯光的散射系数；va和vs为反斯托克斯光和斯托克斯光的频率；aa和as为反斯托克斯光和斯托克斯光在光纤中的传播损耗；L为传播距离。

反斯托克斯光和斯托克斯光的温度调制函数之比的表达式为：

式中：h代表普朗克常数，h＝6．626×10－34J·S；k代表波尔兹曼常数，k＝1．380×10－23J·K－1；Δv代表拉曼频移量，Δv＝1．32×1013Hz；T是开尔文（Kelvin）绝对温度。比较温度T和T0下的光强比Fas－s（T）和Fas－s（T0），我们可以得到温度T的表达式为：

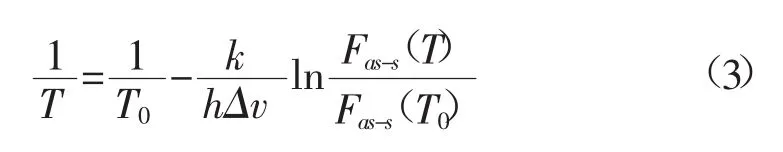
1．2 自适应模糊温度预测原理

自适应模糊温度预测法（AFTPM）认为，从t时刻到t＋1时刻的温度变化与t时刻与过去时刻之间的温度变化相关。在t＋1时刻的温度与t时刻的温度相关性最高。如果在过去的几个时刻里温度趋势在上升，我们认为下一时刻温度会升高。如果过去几个时刻里气温呈下降趋势，我们认为下一时刻温度会降低。我们使用温度在t时刻作为预测基准，利用t－1时刻及之前的历史温度进行训练，来预测t＋1时刻的温度。在预测t＋2时刻的温度时，将t时刻的温度也加入历史数据，并对预测规则进行更新。基于在线学习的AFTPM包括以下八个步骤：

（1）论域的确定

根据历史时刻温度的最大值Tmax和最小值Tmin设置论域U，如式（2）所示，其中D1和D2根据预测精度由自己定义，用于调节论域的范围。

（2）模糊集的划分

针对论域等间隔划分成n份，得到u1，u2…un，n由自己给定，该数量与后续设定的模糊集的数量相同。

（3）确定模糊集和隶属函数

模糊集可以描述为：

其中，μAi是模糊集Ai的隶属度函数，这里选用三角隶属函数，μAi（uj）表示uj在Ai中的隶属度。

假设n＝3，变量温度用模糊集可以表示为A1＝温度低，A2＝温度适中，A3＝温度高。

（4）对历史数据进行模糊化

对每一个历史温度进行模糊化，确定其隶属的模糊集Ai：

（5）根据历史经验设计模糊规则Ai→Aj

（6）根据模糊规则求解模糊关系矩阵R

模糊规则如表1所示：

表1 模糊规则对应表

模糊关系矩阵为：

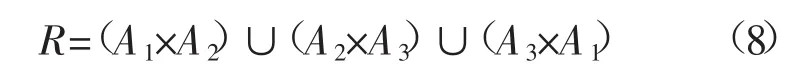
（7）预测

先对当前时刻的值进行模糊化，并根据当前时刻温度的模糊值，预测下一时刻温度的模糊值，再对Apre进行解模糊。

（8）解模糊

我们只信任预测模糊值的最大值。如果最大值只有一个，那么就取对应模糊集的中点，然后再乘以最大值的数值。如果有k个，对应模糊集中点相加除以k。基于在线学习的AFTPM流程图如图2所示。

图2 基于在线学习的AFTPM流程图

2 实验结果

如图3所示为被测光纤第638m位置处实时测量温度和预测温度曲线图。在图3中，蓝色曲线表示实际测得的温度，红色曲线表示预测的温度，温度值都是经过自适应阈值小波包去噪的结果[11－12]，可以看出，蓝线和红色基本重合，预测结果比较准确。图3（b）显示了预测温度与实际测量温度之间的测量误差，结果表明连续测量230分钟内平均预测温度的绝对误差为1．25℃，平均预测误差百分率为3．6%，预测误差的波动范围约为±3．5℃。根据测温结果，AFTPM预警模型可以很好地测量实际温度并预测下一时刻的温度趋势，系统参数符合很多工程例如井下测温预警等要求。若想进一步提高预测精度，减少误差，我们可以通过增加系统检测频率来实现。

图3 被测光纤第638m位置处实时测量温度和预测温度曲线图

图4为不同超前点数w对预测精度影响的结果图，展示了在不同w的下的实际温度信号和预测温度信号的差异。如果RDTS系统以一分钟的时间间隔收集光纤沿线的温度信息，若w取1，则AFTPM可以预测从当前温度开始一分钟后相同位置处的温度；若w取2，可以预测两分钟后相同位置处的温度；若w取n，则可以预测n分钟后相同位置处的温度。因此，若想要提高超前预警时间，可以通过增大超前点数w的值来实现。从图4（a）中可以看出，当w的值较小时，实际温度信号和预测温度信号几乎沿同一趋势变化，二者之间的温度差值也很小，这意味着信号的重合性很好，测量精度较高。随着w值的增加，当w取8时，预测温度出现明显振荡，表明测量精度下降了，实验结果如图4（d）所示。这说明w的值并不是越大越好，w的值越大，超前预警时间更长，但测量误差也会随之增大，使用时应根据实际应用场景来选取w的值。

图4 不同超前点数w下的实际温度与预测温度图

从图4的结果还可以看出，在100分钟、175分钟以及215分钟的时候，预测的温度误差比较明显，造成这种现象的原因是实际温度值发生了较大的变化。

为了提高在温度变化较大时的预测精度，本文提出了基于在线学习的AFTPM，其实验结果如图5所示。将实时测量的温度数据存入历史数据中，不断更新训练数据库，使其能实时捕捉到温度变化信息，从而预测得到更加准确的温度数值。图5（a）显示了未采用在线学习的预测结果，图5（c）展示了未采用在线学习的误差结果，可以明显看出，三个温度变化较大的位置误差越来越大。而采用了在线学习之后，误差基本趋于稳定，不会出现较大波动，预测的精度也显著提高，如图5（b）、5（d）所示。结果表明平均预测温度的绝对误差从1．6℃降到1．1℃，平均预测误差百分率从4．31%降到3．06%，最大误差值从6．9℃降到2．6℃，预测误差的波动范围降到约为±2．6℃。

图5 基于在线学习的AFTPM温度曲线图

以上针对的是单点测量，在实际应用中，我们可以根据需求预测任何位置的温度值，即分布式预测。图6为2D温度颜色图，图上显示了光纤沿线不同位置的温度变化，以及光纤同一位置处不同时间的温度变化。从图中可以看出，550m到750m这一段光纤温度随时间发生明显变化，展示了温度从常温升到67℃，随之慢慢降温到24℃，再升温到45℃，降到室温之后继续加热到58．5℃，最后降到室温的过程，而未进行温度控制的光纤一直处于常温状态。实验中总共测量232组数据，取前160组数据作为历史数据，对剩下的测量数据进行温度预测。图7为实际和预测温度颜色图，其中（a）为2D实际温度颜色图，（b）为2D预测温度颜色图。对比两图，可以看出预测温度值和真实温度值是完全相同的，说明基于在线学习的AFTPM能够准确预测拉曼分布式光纤温度。

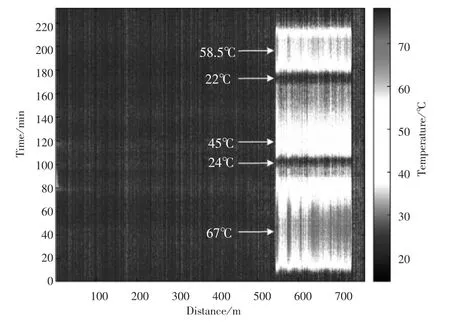
图6 2D温度颜色图

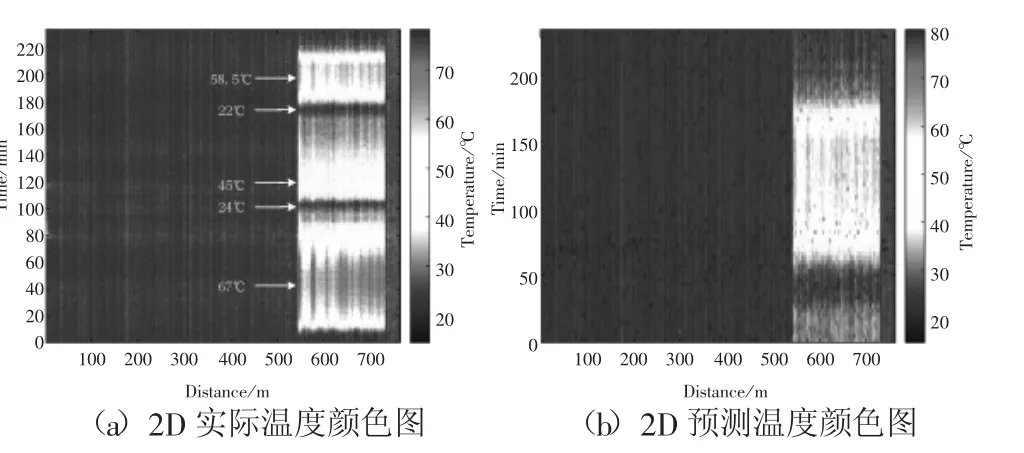
图7 实际和预测温度颜色图

3 结论

本文提出并通过实验证明了基于RDTS系统面向火灾预警的基于在线学习的AFTPM。AFTPM通过分析RDTS系统的温度数据，不仅能快速响应实时温度，还能超前预测未来温度。系统警告时间取决于系统单次解调时间和超前点数的选择。当系统设置超前点数为2时，平均预测温度的绝对误差为1．1℃，平均预测误差百分率为3．06%，预测误差的波动范围约为±2．6℃。

本文通过分析超前点数的大小与超强预警时间和预测精度的关系来选取合适的w值，从而在保证预测精度的同时提高预警时间。为了保证温度变化较大时的预测精度，控制预测误差在小范围内波动，在原本的AFTPM基础上加入在线学习过程，通过分析在线学习算法使用前后的预测误差，从而证明该算法的加入能够有效降低预测误差，尤其是在温度变化较大的位置。我们还对被测光纤沿线上每个位置进行了分布式预测，得到的预测温度基本吻合。

针对高精度应用场景，本文所采用的基于在线学习的AFTPM对预测精度仍有改进的潜力，我们需与时俱进，不断改进。