基于模型预测控制的五相双级矩阵变换器共模电压抑制＊

沙豪杰，耿强

（天津工业大学电气工程学院，天津 300387）

电力变换器随着功率开关器件开关状态的变化，会产生不同幅值的共模电压CMV，当CMV作用于电机端子时，不仅损坏电机绕组绝缘性，缩减电机使用寿命，而且会产生电磁干扰，影响周围设备的正常运行[1－4]。因此，近年来共模电压问题得到众多学者的广泛关注，共模电压抑制技术已应用于不同电力变换器，如三相逆变器、多相逆变器和矩阵变换器[5－7]。通过在变换器输出侧添加共模电感器等无源器件可以有效抑制CMV，但这种增加额外硬件的方法，使得变换器系统的体积、重量和经济成本增加[8]。因此为了避免采用无源滤波器的硬件方法，可以通过改进控制策略减小CMV幅值，这种软件方法在工业应用中更具有意义。

软件方法抑制CMV的基本思想是避免使用可以产生高幅值CMV的开关矢量。目前，传统三相VSIs和多相VSIs抑制输出CMV方法的研究已取得较大进展，抑制多相直接矩阵变换器（DMC）输出共模电压的调制策略被众多学者提出[9－12]。文献[13]提出一种三相－五相DMC在过调制区抑制CMV的控制策略，在调制过程中，只选择大电压矢量，使系统电压传输比增加至0．866，工作在过调制区，共模电压幅值减小至原来的18%，但对输出电流引入较大谐波含量。三相－五相双级矩阵变换器（TSMC）系统CMV抑制策略主要基于SVPWM和载波PWM调制算法。文献[14]针对系统高调制区和低调制区提出两种改进的SVPWM调制策略，在调制比大于0．5257时，整流级选用相邻三个电流矢量，逆变级选用相邻四个大矢量，并且无零矢量，在高调制区抑制CMV。当调制比小于0．4553时，整流级选用间隔电流矢量，逆变级采用四个大矢量和相反方向大矢量代替零矢量，实现低调制去抑制CMV。两种方法将CMV幅值减小为输入电压幅值的47%。但由于逆变级在调制过程中缺少零电压矢量，整流级需要进行四步换流，操作过程较为复杂。因此，文献[15]提出将逆变级零矢量放置在整流级，实现抑制CMV的同时，整流级可以实现零电流换流。该方法是目前最新提出的基于SVM算法抑制CMV，但共模电压幅值被抑制为原来的27．9%。以上算法是基于改进空间矢量调制实现抑制共模电压，并且系统处于开环控制状态。

本文提出一种基于虚拟矢量的FCS－MPCC算法，根据五相TSMC开关状态与CMV之间的关系，以实现抑制CMV和消除xy空间下谐波分量为目标，采用大矢量与方向相反的小矢量合成虚拟矢量，得到十个虚拟矢量作为控制集。本文所提方法不仅可以降低共模电压幅值和消除xy空间下的谐波分量，还有效降低了控制算法的计算量。

1 五相TSMC系统数学模型

五相双级矩阵变换器（TSMC）系统拓扑结构如图1所示，主电路由整流级和逆变级组成，整流级由6个双向开关模块组成，逆变级为五相两电平逆变器拓扑。整流级为电流源型三相整流器，逆变级为电压源型逆变器，在对五相TSMC进行控制时，需要确保三相输入电源不存在短路阻感负载与开路情况。

图1 五相双级矩阵变换器拓扑结构图

对于五相双级矩阵变换器整流级对应的开关模型，以三相输入相电压ui和直流环节电流idc为输入量，三相输入相电流ii和直流环节电压udc为输出量，可得整流级的开关模型为：

式中，Sri（i＝1，2，3，4，5，6）为整流级6个双向开关状态，ui＝[uiauibuic]T；ii＝[iiaiibiic]T。

三相输入电压波形如图2所示，将输入电压划分为6个扇区，以第一扇区为例，相电压：uia＞uib＞uic，存在线电压uiab、uiac和uibc满足整流级输出电压udc＞0的要求，线电压对应的整流级开关状态分别为Sr1Sr5、Sr1Sr6和Sr2Sr6。同理，可以得到其余五扇区对应的整流级开关状态，如表1所示，每个扇区均有三种开关状态符合整流级的约束条件。

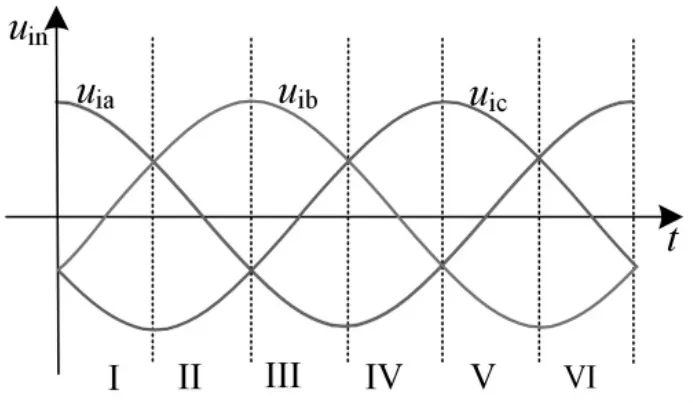
图2 整流级输入电压扇区分布图

表1 直流侧电压为正的开关组合

逆变级拓扑结构为五相两电平逆变器，由10个开关管组成，总的开关状态组合有32种，因此逆变级存在32个电压矢量，其中包括30个有效电压矢量和2个零电压矢量。定义开关函数Sk＝1（k＝A，B，C，D，E）时，代表对应相的上桥臂IGBT导通，Sk＝0时代表下桥臂IGBT导通，可以得到相电压与开关函数之间的关系为：

输出五相电压经过坐标变换可以得到两相静止坐标系下的空间电压矢量：

式中，uA、uB、uC、uD、uE为输出五相电压，uo（αβ）和uo（xy）分别为αβ空间和xy空间输出参考电压。

五相逆变级的空间电压矢量，映射在两个正交坐标系下，即基波子空间矢量坐标系（α－β）和三次谐波子空间矢量坐标系（x－y），如图3所示。

图3 五相逆变级电压矢量分布图

根据基波空间矢量坐标系（α－β）下的电压矢量根据电压矢量幅值共可分为四组，即大电压矢量（VL＝0．6472udc）、中电压矢量（VM＝0．4udc）、小电压矢量（VS＝0．2472udc）和零电压矢量（V0，V31）。

对于五相逆变级，将输出相电流io和直流环节电压udc作为输入量，输出相电压uo和直流环节电流idc作为输出量，可以得到对应的开关模型为：

式中，Sij（j＝1，2，…9，10）为逆变级10个开关器件的开关状态，io＝[iAiBiCiDiE]T；uo＝[uAuBuCuDuE]T。

五相双级矩阵变换器整流级开关状态共存在9种情况，但需要满足整流级的约束条件，因此在每个扇区只有三种开关状态满足要求。五相逆变级采用FCS－MPCC算法时，控制集的选择可采用31个电压矢量（VL，VM，VS，V0或V31）、21个电压矢量（VL，VM，V0或V31）或者11个电压矢量（VL，V0或V31），为了获得更加优良的输出性能，一般采用31个电压矢量作为控制集。但由于整流级和逆变级两部分需要耦合控制，整个五相双级矩阵变换器的开关状态共存在3×31（93）种，可以看出数字控制器的运算负担较大。

根据图1所示滤波器的拓扑结构，可以得到输入滤波器的数学模型：

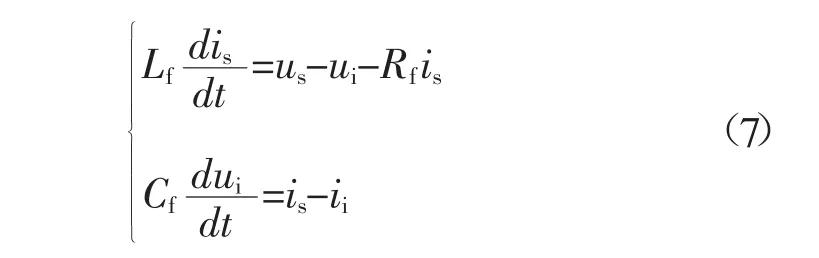
式中，Lf、Cf和Rf为输入滤波器参数，us和is分别为网侧电压和网侧输入电流。

五相阻感负载对应的五相电压与阻感负载之间的关系为：

对五相电压进行Clarke坐标变换，得到在两相静止坐标系下的电压表达式：

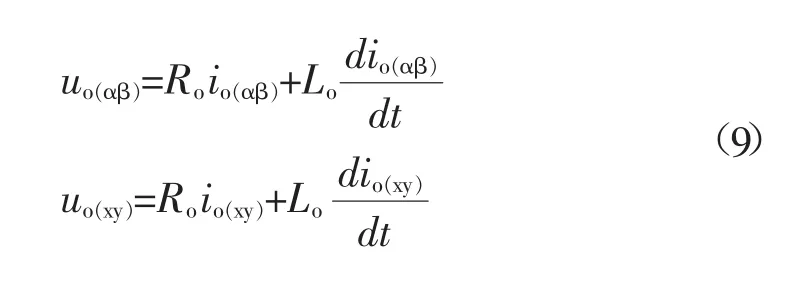
2 五相TSMC共模电压抑制策略

2．1 五相TSMC预测模型

根据上一节对五相双级矩阵变换器系统数学模型的分析，对输入滤波器模型和输出负载模型的连续状态方程进行离散化，实现对控制变量在下一时刻变量值的预测。

对于输入滤波器，将式（7）转变成离散状态方程组为：

式中，ui（k＋1）为变换器输入侧电压在k＋1时刻的预测值，is（k＋1）为变换器输入侧电流在k＋1时刻的预测值，Φ＝eATs，Γ＝A－1（Φ－1）B。其中：

对于输出五相阻感负载对应的输出电流，利用前向欧拉公式得到负载的离散数学模型：

式中，Ro和Lo分别为负载阻值和电感参数，Ts为系统离散控制周期，io（k＋1）为变换器输出电流在下一时刻的预测值。

经过Clarke坐标变换，可以得到预测电流在αβ和xy子空间下的表达式：

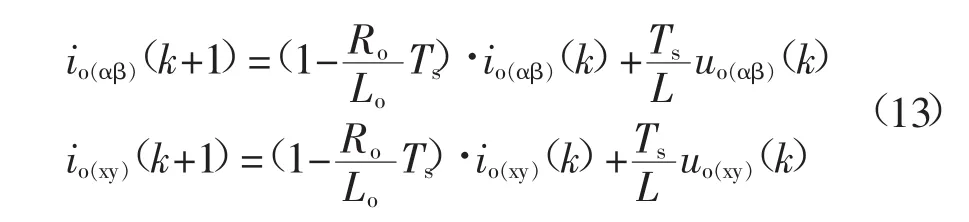
2．2 抑制共模电压控制集的构造方法

五相TSMC输出共模电压为负载中性点与网侧电源中性点之间的电压差，共模电压与输出五相电压之间的关系为：

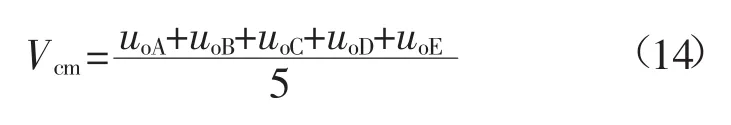
由公式（1）、（3）、（6）和（14）得到CMV与整流级和逆变级开关函数之间的关系为：

根据式（15）可以看出共模电压幅值取决于整流级和逆变级的开关状态，两级不同的开关状态组合对应不同的共模电压幅值，以整流级和逆变级输出矢量均位于第一扇区为例，如表2所示。

表2 不同矢量组合下产生的共模电压

通过对五相逆变级电压矢量与输出CMV幅值进行分析，大电压矢量和小电压矢量对应共模电压幅值最小，因此可以选择大电压矢量和与之相反的小电压矢量构造虚拟矢量，构造原理如图4所示。在基波空间下合成虚拟矢量的同时，使三次谐波空间下合成虚拟矢量幅值为零。根据伏秒平衡原理，虚拟矢量在αβ和xy子空间的幅值可以表示为：

图4 虚拟电压矢量构造原理图

式中，Vv1（αβ）和Vv1（xy）为Vv1在αβ和xy空间下的幅值，λ为大矢量的占空比。

为了消除谐波空间分量，即在谐波空间下的虚拟电压幅值Vv1（xy）＝0，即：

直流环节电流为两个矢量对应的直流环节电流之和为：

式中，idc1和idc2分别为大电压矢量和小电压矢量作用下的直流环节电流。

同理，其他9个虚拟电压矢量在两个空间坐标系下的分布，如图5所示。

图5 虚拟电压矢量空间分布图

根据虚拟矢量空间分布，可以发现虚拟矢量Vv1与所用合成的基本大电压矢量V25同向，以虚拟电压矢量Vv1中基本电压矢量作用顺序为例，合成虚拟电压矢量由两个基本电压矢量合成得到，λ为大电压矢量V25的占空比，其脉冲序列如图6所示。

图6 虚拟电压矢量Vv1脉冲序列

当大小两个基本矢量合成虚拟矢量时，消除了谐波空间下的谐波分量，因此输出电流只包含基波分量，根据公式（13），可以得到预测电流在αβ和xy子空间下的表达式：

因缺少基本零电压矢量，可以采用两个相反大矢量合成虚拟零矢量进行替代，以虚拟矢量Vv1对应的虚拟零矢量为例，在基波空间下大矢量V25和V6合成虚拟零矢量。根据前一个采样周期的虚拟电压矢量Vpre，选择虚拟零矢量，规则如表3所示。

表3 虚拟零矢量构造原则

2．3 价值函数寻优算法实现

五相TSMC开关状态根据价值函数最优原则进行选取，价值函数定义为参考量与预测值之间的误差绝对值为：

式中，xref为控制目标变量的参考值，x（k＋1）为控制目标变量下一时刻的预测值。

根据瞬时无功理论，可以得到在五相TSMC输入侧在k＋1时刻的无功功率：

式中，usαk＋1、usβk＋1、isαk＋1和isβk＋1分别为网侧电压和网侧电流预测值。

由价值函数定义，可以得到关于网侧无功功率价值函数为：

为实现网侧单位功率因数，无功功率参考值为Qref＝0。

虚拟矢量可消除xy谐波空间的谐波分量，因此逆变级的价值函数简化为：

结合整流级和逆变级两部分的价值函数，定义整个系统的价值函数为：

式中γ为无功功率权重因子。

本文以大电压矢量和反向小电压矢量合成的虚拟电压矢量作为控制集，提出了改进的FCS－MPCC算法，实现了抑制CMV和消除xy空间下谐波分量。基于模型预测电流控制算法抑制五相TSMC输出CMV控制原理如图7所示。

图7 基于虚拟电压矢量模型预测电流控制原理图

3 仿真结果分析

为了验证本文所提控制方法的正确性，在此将采用常规31矢量的FCS－MPCC算法进行对比分析，该方法命名为31－FCS－MPCC，所提出的基于虚拟矢量的算法命名为VV－FCS－MPCC。五相TSMC系统参数如表4所示。

表4 系统仿真参数

3．1 相同采样频率的稳态性能比较

为了验证所提方法在相同采样频率（20KHz）下的可行性，进行了仿真验证。图8为五相双级矩阵变换器在两种不同算法下网侧输入电流和无功功率波形，可以看出两种不同控制方法都可以实现单位功率因数，并给出网侧电流THD分析结果，所提出的VV－FCS－MPCC算法增加了网侧电流谐波含量。图9为系统输出共模电压波形，可以看出传统31－FCS－MPCC算法输出CMV幅值较大，而本文提出的VV－FCS－MPCC控制算法将输出共模电压幅值降低至输入电压幅值的0．52倍。图10为五相TSMC输出电流和线电压波形，并对输出电流进行FFT分析，可以看出本文所提方法有效降低了输出电流谐波含量，并且输出电流跟踪误差由0．12A变为0．03A。

图8 网侧输入电流与无功功率波形

图9 输出共模电压波形

图10 输出电流与线电压波形

本文所提算法对应的输出电流在基波空间和谐波空间下的电流轨迹如图11所示，可以看出本文所提策略能够有效抑制三次谐波电流，并且输出电流纹波较小。为验证所提VV－FCS－MPCC在各参考电流幅值下的控制性能，与传统31－FCS－MPCC算法分别采用参考电流幅值为1A、2A、3A和4A时，对网侧和输出电流的谐波含量进行结果分析，如图12所示。通过对比结果得知此方法可以有效降低输出电流的谐波含量，提高了系统输出性能。

图11 不同参考电流幅值下电流THD值比较

图12 不同参考电流幅值下电流THD值比较

3．2 动态性能比较

对于模型预测控制算法最为突出的特点为具有良好的动态跟随性，为验证采用本文提出控制方法的动态性能，通过分别在线改变参考输出电流幅值和频率，当给定参考电流由幅值0突变为幅值3A、参考电流频率由20Hz突变为50Hz时，对应的电流及CMV波形如图13和图14所示。可以看出对于本文提出的基于虚拟电压矢量的模型预测算法输出电流跟随性，由放大图可以看出跟随能力仍然较好，只出现跟踪较小延迟时间，但对电流变化的影响较小。

图13 参考电流幅值突变动态仿真波形（0－3A）

图14 参考电流频率突变动态仿真波形（20－50Hz）

4 结论

本文基于虚拟电压矢量，提出抑制五相TSMC系统输出CMV的模型预测电流控制算法，将CMV幅值有效抑制为输入电压的0．52倍，并改善输出电流波形质量。所提算法的动态性能良好，以输入无功功率和输出电流作为控制目标，保证了系统良好的输入输出性能，当参考电流发生突变时，可以实现输出电流在较短时间内跟随参考电流。