地震作用下液化场地变截面桩与等截面桩的动力响应对比分析
2022-08-04冯忠居王逸然张俊波张建斌孟莹莹赵瑞欣
冯忠居,王逸然,张俊波,张建斌,孟莹莹,赵瑞欣
(1.长安大学公路学院,陕西西安 710064;2.厦门路桥工程投资发展有限公司,福建厦门 361006)
引言
地震是一种破坏力极强的自然灾害,我国近一半处于抗震设防烈度为Ⅶ度及以上的高设防烈度区。采用桩基础穿过地下可液化土层可增强建筑物的抗震性和稳定性,避免地震对建筑物造成的危害[1-2]。但是在强震作用下处于液化场地的桩基础因砂土液化破坏严重,从而严重威胁整个桥梁的运营安全。
国内外学者对可液化场地桥梁桩基础动力响应问题进行了深入研究。理论方面:LAORA 等[3]通过模拟、分析和提出Winkler 地基梁的简化模型、物理概念和计算液化场地桩基础有效长度的方法,研究了桩基础的动力响应问题;马亢等[4]在分析桩基础弯矩影响因素的基础上,通过运用量纲分析方法研究出6个无量纲π 式,计算与预测了处于均质土体中的桩基础因地震产生的弯矩峰值;张建民等[5]和王刚等[6]根据循环剪切过程中饱和砂土层体积应变三分量的变化特征,构建了液化后饱和砂土层特大变形的循环弹塑性模型,为液化后砂土层特大变形的定量描述奠定基础。
在试验方面:冯忠居等[7-10]通过模拟大型振动台试验,分析并研究了处于液化场地桩基础在不同地震动强度作用下的动力响应规律;唐亮等[11]利用振动台对处于液化场地桩基础进行响应模型试验,研究了群桩在地震动强度作用下的动力反应;冯士伦等[12]通过模拟在地震作用下饱和砂土层桩基础的大型振动台试验,研究液化条件下桩基础在不同地震动作用下的动力响应问题,并对液化饱和砂土的p-y 曲线进行分析;李雨润等[13]通过振动台模型试验考察了液化砂土层的动力响应特性,依据API规范方法,修正了土体原始模量和其极限反力,构建p-y 曲线计算公式以满足工程实例的需要,并根据振动台试验提供的数据选用FLAC3D 建模软件进行数值模拟,验证其精确性;孔锦秀[14]通过数值模拟与离心模型试验,研究了在不同地震动强度作用下处于液化场地的桥梁桩基础及其上部结构的动力响应特性,并分析了地震动参数与各响应之间的联系。在数值模拟方面:冯忠居等[15-16]考虑桩土的相互作用,结合具体工程实例,采用有限元软件建立模型,分析不同地震波作用下桩的动力响应,并将其结果对桩基在强震作用下的安全进行评价;刘星等[17]利用饱和砂土液化后特大变形模型,描述了液化场地土层的应变关系,构建了三维群桩计算模型,分析了桥梁桩基础在地震作用下的动力响应特性;孔德森等[18]通过FLAC3D有限元分析软件,建立了在地震作用下群桩-土相互作用的模型,分析了土体孔压比的变化、桩基的实时受力、弯矩与位移;李雨润等[19-21]在砂土液化振动台试验的基础上,利用有限差分软件对不同波型及加速度下群桩的侧向动力响应特性进行数值模拟,其结果与试验结果相符;邹佑学等[22]结合砂土液化本构模型,应用FLAC3D 软件分析了桩与土的变形及应力;高盟等[23]和孔德森等[24]通过数值模拟建立了扩底桩、等截面桩及液化场地倾斜桩-土模型的三维模型,对比分析了各桩基的动力p-y曲线;NAEINI等[25]通过建立数值模型,研究了在不同地震作用下桩基础的侧向位移及弯矩;王圭华等[26]采用数值模拟的方法研究了大直径桩-土相互作用,并求解了土动力平衡方程。
目前,国内外学者主要研究在地震作用下由于砂土液化对桥梁等截面桩基础的破坏,关于变截面桩基础的动力响应方面研究很少,所以对液化场地变截面与等截面桩动力响应特性的研究十分必要。本文结合厦门第二东通道工程,采用有限元软件建立数值模型,分析在地震作用下不同变截面位置变截面桩的桩身加速度、位移、弯矩及剪力,并与相同条件下的等截面桩进行对比,为液化场地桥梁变截面桩基础的抗震性能研究提供依据。
1 工程概况
厦门第二东通道A2 施工标段(K23+805.000~K27+105.300)中的海域桥梁段为K24+915.300~K27+105.300段。该标段有特大桥1座和大桥4座(含互通主线桥),这些桥梁的桩基穿越淤泥、淤泥质粉质黏土及细砂、中砂等属软弱土层。
翔安大桥地区地震设防烈度为Ⅶ度,在50 a设计基准期内,超越概率10%的地震加速度为0.15 g。本文选取砂土层厚度最大的H15#墩展开研究,H15#墩的桩基础由6根大直径变截面深长桩构成,横向三排,横向中心距7.6 m,顺桥向中心距6.25 m,桩基均为变截面钢管混凝土复合桩,桩长45 m,桩径为2.50/2.15 m。桩基穿越淤泥质粉质黏土及饱和砂土层,在地震作用下具有产生砂土液化等不利地质条件,H15#墩的桩基础如图1所示。
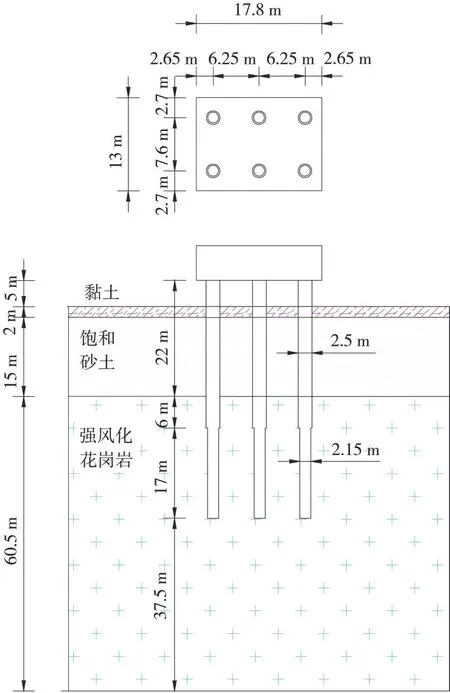
图1 15#墩桩基础图Fig.1 Pile foundation diagram of pier 15#
2 模型建立及参数选取
2.1 模型建立
(1)变截面桩及等截面桩模型建立
尽管实际工程中很少采用单桩基础,为了兼顾工程应用及建立一般理论的需要,考虑到研究单桩动力特性是群桩动力分析的基础,本着研究工作从简单到复杂的过程,本文研究中以H15#墩的桩基础为原型,选用变截面单桩为研究对象。
模型尺寸X 方向52.5 m,Y 方向52.5 m,Z 方向77.5 m。土层由上至下分别为黏土、饱和砂土和强风化花岗岩,其中:黏土层厚度为2 m,饱和砂土层厚度为15 m,强风化花岗岩层厚度为60.5 m,桩长为45 m,变截面桩的桩径为2.50/2.15 m,变截面分别在距桩顶25 m、28 m和32 m处,等截面桩的桩径为2.50 m。单桩布置如图2所示,单桩模型图如图3所示。

图2 单桩布置图Fig.2 Single pile layout
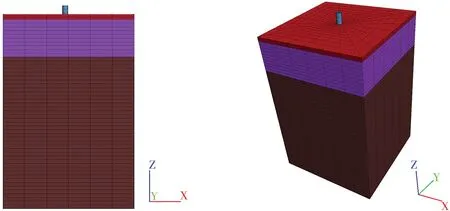
图3 单桩模型图Fig.3 Section of single pile model
(2)本构模型确定
数值模拟中桩基采用弹性体和桩周岩土体适于岩土力学的通用模型摩尔-库伦弹塑性模型,动力与地下水的耦合计算中采用Finn 模型。Finn 模型的实质是在Mohr-Coulomb 模型的基础上增加了动孔压的上升模式,并假定动孔压的上升与塑性体积应变增量有关,塑性体积应变Δεvd仅是总累计体积应变εvd和剪应变γ的函数。
2.2 参数选取
依据《厦门第二东通道地质勘察报告》土层材料参数见表1,流体参数及液化参数见表2,桩体参数见表3。

表1 土层材料参数表Table 1 Parametersof each material

表2 流体参数及液化参数表Table 2 Fluid parameters and liquefaction parameters table

表3 桩体参数表Table 3 Table of pile parameters
2.3 边界条件
在满足有限元模拟软件的计算精度要求下,规定桩侧土体距离桩轴为10 倍桩径,桩端距离底部边界为15倍桩径[27]。在静力计算时,固定模型四周及底部的边界,模型的顶面为自由边界,为自重应力作用下的平衡计算提供条件;在动力计算时,模型采用自由场边界,在土体周围生成网格。边界条件如图4所示[28]。

图4 边界条件Fig.4 Boundary conditions
3 计算方案
3.1 地震波的选取
根据《厦门第二东通道工程场地地震安全性评价报告》,拟建场址位于0.15 g分区内,地震的基本烈度为Ⅶ度。因此,地震动输入采用50 a 超越概率10%(5010)地震波。经过处理后的5010 地震波如图5 所示,地震波动频谱如图6所示。

图5 (5010)地震波Fig.5 (5010)seismic wave

图6 (5010)地震动频谱Fig.6 (5010)seismic spectrum
3.2 工况设计
为对比分析液化场地变截面桩与等截面桩的动力响应,计算工况见表4。

表4 计算工况Table 4 Calculates working conditions
4 计算结果分析
4.1 孔隙水压力响应
为分析地震作用过程中土层的液化情况,检测砂土下1 m、10 m 和15 m 处的孔隙水压力。三个不同深度处孔压比如图7所示。
由图7可知:三者孔压比变化规律基本相同,当地震波开始加载时,孔压比的值在0附近,随着地震波的加载,孔压比逐渐增大最后趋于稳定,孔压比达到0.8,土体完全液化[9];孔压比达到峰值的时刻随饱和砂土层深度的增加而滞后,且峰值逐渐减小,砂土下1 m、砂土下10 m 和砂土下15 m 的孔压比峰值分别为1.09、1.03和0.98,其原因为在地震动作用下,砂土层液化是从浅处至深处发育,上层砂土先失去强度发生液化,且受地震作用的影响较大,下层砂土受地震作用的影响较小。

图7 孔压比Fig.7 Pore pressure ratio
4.2 桩身加速度响应
地震作用下,变截面桩及等截面桩的桩身加速度变化规律如图8所示。
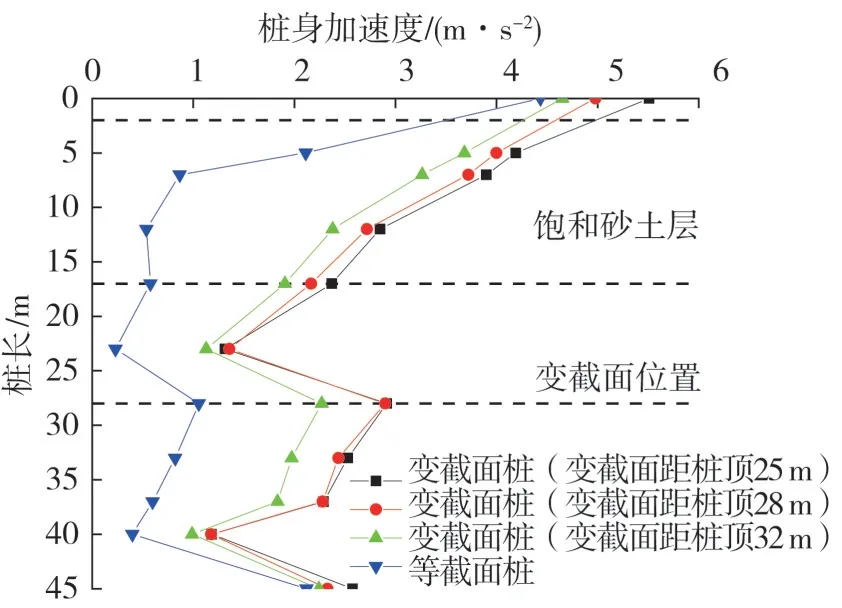
图8 桩身加速度Fig.8 Pile acceleration
由图8可知,在地震作用下,变截面桩及等截面桩的桩身加速度变化趋势一致,自桩端至桩顶总体增加,且均较输入的地震加速度大,其原因是在地震动强度作用下饱和砂土层发生液化,土层强度基本丧失,处于流动状态,液化土体侧向移动,砂土层对桩身的支撑作用很小,地震波由波密介质传输至波疏介质时桩身加速度峰值产生了一定的放大效应;变截面桩的桩身加速度随着变截面位置的下移而逐渐减小,且均大于等截面桩,说明不同截面类型受地震波加速度放大效应的影响程度不同;在2~17 m 的饱和砂土层处,变截面桩增加的速度大于等截面桩,其原因是在地震动强度作用下饱和砂层土发生液化,由于变截面桩下部直径较小的几何特性,整体承载力、强度与刚度较小,相同的地震动能量对变截面桩的影响较大。
变截面及等截面的桩顶加速度放大系数见表5。其中α加速度的放大系数定义为:

表5 桩顶加速度放大系数表Table 5 Acceleration amplification coefficient table of pile tip

式中:αmax为桩身加速度峰值;α′max为输入地震动峰值加速度。
由表5 可知,变截面桩的桩顶加速度放大系数较等截面桩大,其值分别为3.67、3.32、3.1 和2.95,其原因是相对于传统的等截面桩,在受到相同地震动强度作用下,由于变截面桩的横截面尺寸上大下小,整体稳定性较弱,加速度放大效果明显,从而桩顶加速度放大系数较大。
地震作用下,变截面桩及等截面桩的桩顶与桩底加速度时程如图9所示。
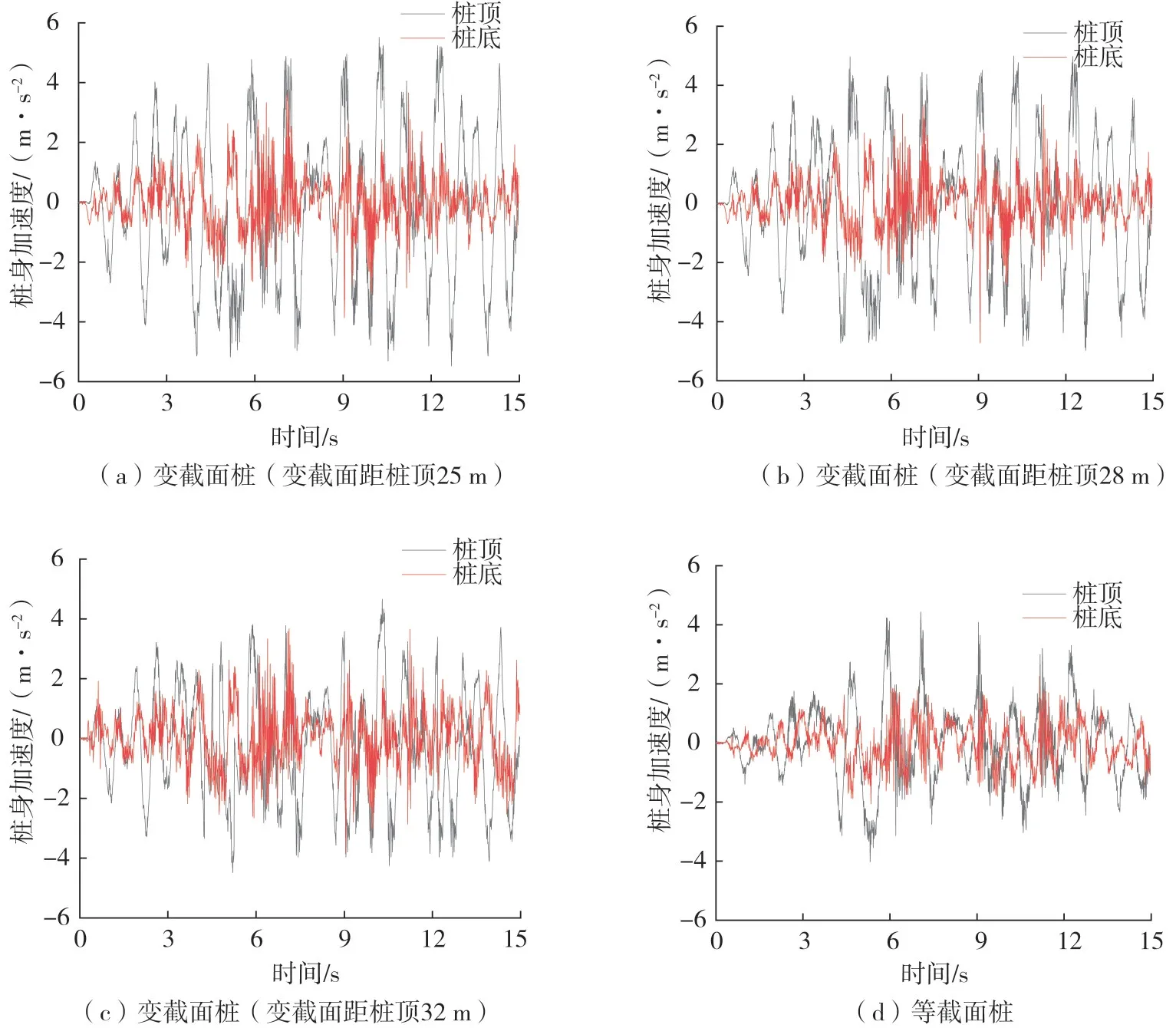
图9 桩顶与桩底加速度时程Fig.9 Acceleration history of pile top and pile bottom
由图9 可知,地震作用下,桩顶与桩底加速度时程变化规律不同,输入地震加速度峰值与桩底加速度峰值相差不大,且小于桩顶加速度峰值,说明上部土层对加速度峰值的放大效应显著大于下部土层。
变截面桩(变截面距桩顶25 m)和变截面桩(变截面距桩顶28 m)、(变截面距桩顶28 m)的桩顶加速度达到峰值的时刻分别为10.17 s、10.29 s和10.43 s,桩底加速度达到峰值的时刻分别为8.89 s、9.05 s和9.19 s,变等截面桩的桩顶和桩底加速度达到峰值的时刻分别为7.06 s和6.09 s,即桩顶加速度达到峰值的时刻均滞后于桩底,其原因是地震波自下往上传递,桩底最先受到地震波的影响,达到加速度峰值的时刻早于桩顶。变截面桩的桩顶和桩底加速度达到峰值的时刻分别滞后于等截面桩,其原因是变截面桩下部直径相对较小,地震波从土层横向传递于桩,由于土层的阻碍作用,变截面桩受到地震波的影响会产生滞后性,并且其加速度峰值较大,从而达到加速度峰值的时刻也相对较晚。
4.3 桩身位移响应
地震作用下,变截面桩及等截面桩的桩身位移及桩顶位移时程响应如图10-11所示。

图10 桩身位移Fig.10 Pile displacement diagram
由图10 可知,地震作用下,变截面桩及等截面桩的桩身位移沿桩长方向逐渐减小,在桩顶处达到最大,变截面桩(变截面距桩顶25 m、变截面距桩顶28 m、变截面距桩顶32 m)和等截面桩的桩顶水平位移分别为39.87 mm、38.54 mm、34.03 mm 和24.45 mm;在饱和砂土层,桩身位移变化趋势均较陡,其原因是在地震作用下饱和砂土层发生液化,液化土体转化为流体向侧向移动,桩-土相互作用导致桩身位移增速较大;变截面桩的桩身位移随着变截面的下移逐渐减小,且大于等截面桩的桩身位移,在桩顶处二者差值最大,其原因是在液化作用下,由于变截面桩自身结构上大下小的特点,其整体强度与刚度较小,因此当输入相同地震能量时产生的变形大于等截面桩。
由图11 可知,地震作用下,不同截面类型的桩基础桩顶水平位移沿桩长方向变化规律不同,前4 s 内等截面桩的桩顶水平位移大于变截面桩的桩顶水平位移,4 s 后变截面桩的桩顶水平位移大于等截面桩的桩顶水平位移;变截面桩(变截面距桩顶25 m)、变截面桩(变截面距桩顶28 m)和变截面桩(变截面距桩顶28 m)的桩顶水平位移达到峰值的时刻分别为12.3 s、12.2 s和12 s,等截面桩的桩顶水平位移达到峰值的时刻为13 s,因此,桩顶水平位移达到振幅峰值时刻随着桩截面类型的变化而变化,变截面桩稍早于等截面桩。
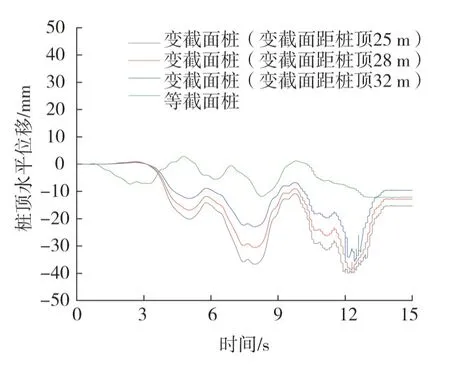
图11 桩顶水平位移时程响应Fig.11 Time-history response of pile top horizontal displacement
4.4 桩身弯矩响应
地震作用下,变截面桩及等截面桩的桩身弯矩如图12所示。
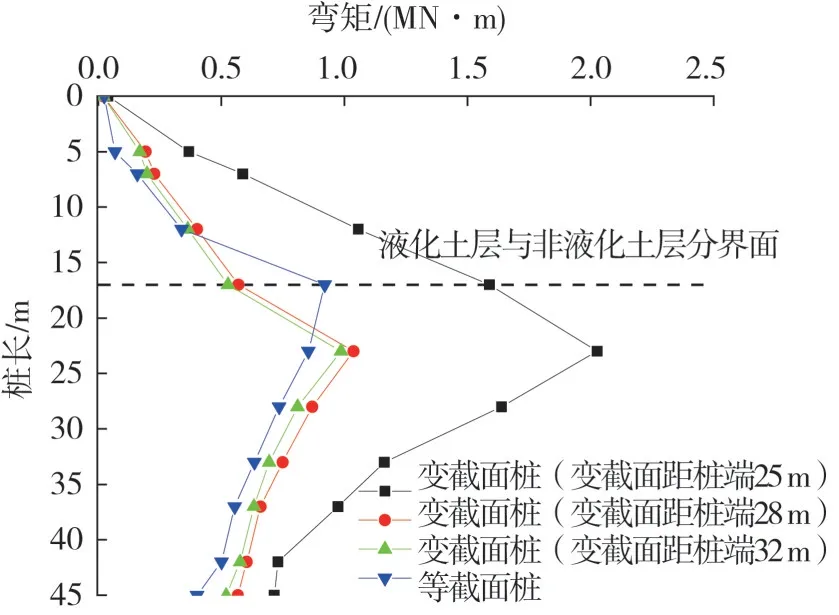
图12 桩身弯矩Fig.12 Pile bending moment
由图12 可知,地震作用下,桩身弯矩沿桩长方向整体呈现先增大后减小的趋势,其原因是当桩与土共同运动发生相互作用时,上部土层水平抗力小并且受挤压产生的变形较大,弯矩随着土层水平抗力的增大而增大,直至等于水平力时,弯矩也随之达到峰值,但之后由于土层的地基反力增大,弯矩又随之减小,变截面桩的桩身弯矩峰值随着变截面的下移逐渐减小,且均较等截面桩大,变截面桩(变截面距桩端25 m、变截面距桩端28 m、变截面距桩端32 m)和等截面桩的桩身弯矩峰值分别为-2.03 MN·m、-1.03 MN·m、-0.99 MN·m和-0.92 MN·m。
等截面桩的桩身弯矩峰值出现在地面以下17 m 位置处,即液化土层与非液化土层分界处,其原因为在地震动强度作用下饱和粉细砂土层发生液化,土层处于流动状态,桩与土运动发生相互作用,导致桩身弯矩较大;而变截面桩的桩身弯矩峰值出现在地下23 m 位置处附近,较等截面桩深6 m,其原因是变截面桩下部减小了桩身横截面积,即改变了横截面的几何特性及内力状态,其弯矩变化规律亦随之变化。
因此,在桥梁桩基础设计时应考虑抗震性,特别是桩基础周围土体存在可液化土层时,应重点分析非液化土层与液化土层分界处及其以下的抗弯能力,确保桥梁桩基础具有足够抵抗地震的能力。
4.5 桩身剪力响应
地震作用下,变截面桩及等截面桩的桩身剪力变化规律如图13所示。

图13 桩身剪力Fig.13 Shear force of pile
由图13可知,地震作用下,桩身剪力沿桩长方向均呈先增大后减小趋势,变截面桩的桩身剪力峰值随着变截面的下移逐渐减小,且均较等截面桩大,变截面桩(变截面距桩端25 m、变截面距桩端28 m、变截面距桩端32 m)和等截面桩的桩身剪力峰值分别为0.79 MN、0.16 MN、0.15 MN和0.12 MN。
等截面桩的桩身剪力峰值出现在地面以下7 m 位置处附近,其原因为在地震动作用下饱和砂土发生液化,砂土层处于流动状态,使地基剪切刚度衰化、动剪切模量下降,液化层侧扩引起桩-土发生相对运动产生作用,致使桩身剪力较大;而变截面桩的桩身剪力峰值出现在地面以下12 m 位置处附近,较等截面桩深5 m,其原因是变截面桩的上半桩的桩身刚度大于下半桩的桩身刚度,使得受相同地震作用时,变截面桩的下半桩承载力较弱,剪力峰值位置随之下移。
因此,液化场地在桥梁变截面桩基础设计时应考虑抗震性,特别是桩基础周围土体存在可液化土层时,应重点分析可液化土层处的抗剪能力,确保桥梁桩基础具有足够抵抗地震的能力。
5 桩基安全评价
5.1 桩身弯矩
根据厦门第二东通道H15#墩桩基础配筋情况,采用截面抗弯验算方法计算得到在可液化地基处桩基础抗弯承载力为2.234 MN·m,以此为基准,对变截面桩及等截面桩的桩身抗弯强度进行安全评价[29]。变截面桩及等截面桩的桩身弯矩峰值均在安全范围之内。
5.2 桩身剪力
根据厦门第二东通道H15#墩桩基础配筋情况,采用截面抗弯验算方法计算得到在可液化地基处桩基础抗剪承载力为0.819 MN,以此为基准,对变截面桩及等截面桩的桩身抗剪强度进行安全评价[29]。变截面桩及等截面桩的桩身剪力峰值均在安全范围之内。综合考虑安全性及经济性,应优先选择变截面桩(变截面距桩端28 m),既存在一定的安全富裕又能达到减少材料降低成本的效果。
6 结论
(1)地震作用下,液化土层不同深度处的孔压比变化规律基本相同,均从0逐渐增大最后趋于稳定;孔压比达到峰值的时刻随饱和砂土层深度的增加而滞后,且峰值逐渐减小。
(2)地震作用下,变截面桩及等截面桩的桩身加速度均自桩底至桩顶整体呈现增大趋势,较输入的地震波加速度大;变截面桩的桩身加速度均大于等截面桩,且变截面桩的桩顶和桩底加速度达到峰值的时刻均早于等截面桩。
(3)地震作用下,变截面桩及等截面桩的桩身位移在桩顶处最大,且变截面桩的桩身位移大于变截面桩,在桩顶处二者差值最大;变截面桩桩顶水平位移达到振幅最大值的时刻早于等截面桩。
(4)地震作用下,桩身弯矩沿桩长方向均整体呈先增大后减小的趋势,等截面桩的桩身弯矩峰值出现在液化土层和非液化土层分界处,而变截面桩的桩身弯矩峰值出现在液化土层和非液化土层分界面以下6 m处,桩身弯矩峰值均在安全范围之内。
(5)地震作用下,桩身剪力沿桩长方向均呈先增大后减小趋势,变截面桩及等截面桩的桩身剪力峰值均出现在液化土层,但变截面桩的桩身剪力峰值位置较等截面桩深,桩身剪力峰值均在安全范围之内。
(6)液化场地桥梁变截面桩基础抗震设计时,应着重考虑液化土层与非液化土层分界面以下的抗弯能力设计及液化土层中抗剪能力设计,在满足安全性能的条件下,应优先选择变截面桩,以达到缩短工期及降低工程造价的效果。
