基于超声背散射信息熵成像的微波消融凝固区检测方法

夏涛，周著黄，宋爽，王赫，吴水才

北京工业大学 环境与生命学部，北京 100124

引言

我国是全球肝癌发病率最高的国家，肝癌死亡率仅次于胃癌、肺癌，是第三大常见恶性肿瘤，严重危害人类生命健康[1]。因此，肝癌的早期诊断和治疗具有重要意义。目前，肝肿瘤的治疗方法主要有手术切除、肝脏移植和经皮热消融[2]。由于临床上肝脏稀缺、手术创伤大等原因，热消融成为治疗肝肿瘤的有效方法。将消融针插入肿瘤内作为热源，通过加热使肿瘤组织温度升高到60℃以上，从而使肿瘤组织凝固坏死，达到杀死肿瘤的目的。微波消融治疗被认为是目前最成熟、先进的局部消融技术之一，具有局部肿瘤灭活效果好、创伤小、能最大限度地保留肝脏功能等优点，已应用于临床治疗。为了保证消融的安全性，提高消融的准确性，需要对消融过程进行监测。超声因其无损、实时、廉价等优点，已成为监测热消融的主要技术之一。但是，传统B 超成像分辨率低，且容易受到加热过程中气泡的影响，不能准确地对凝固区进行监测。

为了克服传统B 超的局限性，更好地对凝固区进行检测，需要更为精准的超声成像方法。在声学上，生物组织可以看作散射子的集合。超声背散射回波信号具有一定的随机性，通过分析背散射信号的统计分布，寻找适合的数学模型对组织中的散射子进行参数成像，可以对凝固区进行检测。Nakagami 参数成像[3-4]、超声零差K 成像[5-6]都已应用于凝固区的检测。但基于模型的参数方法需要背散射数据符合所使用的统计分布模型，对于不同型号的超声设备，得到的超声回波信号会各不相同；在超声背散射回波信号的处理过程中，不同的压缩方法也会改变信号的分布，这些都会使背散射数据不能一直满足所使用的分布模型。因此，需要一种更为灵活的统计参数方法。

信息熵作为一种基于非模型的参数统计方法，不需要超声背散射信号符合特定的统计分布模型，是一种更灵活的成像方式。Hughes 等[7-9]首次提出利用信息熵来分析超声信号，并证明了熵值可以定量描述散射介质的微观结构变化。近年来，超声信息熵成像也得到了进一步的研究。Zhou 等[10]研究表明小窗口熵成像在脂肪肝评估中比传统的B 模式超声成像和Nakagami 成像效果更好。Chen 等[11]评估了信息熵和深度学习在肝脂肪变性分级中的临床价值；对原始数据进行信息熵成像，使用VGG-16 模型进行训练和预测，并与组织学检查结果比较，发现背散射统计信息熵可用于肝脂肪变性的超声诊断，不仅提高了肝脂肪变性的分级性能，而且可用于肝脂肪变性的临床解释。Lin 等[12]研究了非酒精性脂肪性肝病（Nonalcoholic Fatty Liver Disease，NAFLD）和代谢综合征的超声熵成像之间的关系，并与声结构量化（Acoustic Structure Qualification，ASQ）的超声熵成像进行比较。证明超声熵成像可以提供肝脂肪变性的信息。特别是超声熵成像可以描述NAFLD 个体的代谢当量风险，并且优于传统的ASQ 技术。

目前，超声信息熵成像在凝固区检测方面还未有研究报道。本文对背散射信号进行处理，利用滑动窗口技术进行信息熵成像，通过多项式拟合技术测量凝固区面积，与金标准进行比较验证算法的准确性。

1 材料与方法

1.1 信息熵

信息熵是一种基于非模型的参数统计方法，不需要考虑数据分布，对各种信号特征的适应性更强，在成像和描述背散射统计信息方面更加灵活[13]。在超声成像中，背散射数据（射频信号或包络信号）都是通过对连续函数y=f(t)进行采样得到的，背散射数据的信息熵被定义为背散射数据概率密度分布函数w(y)对数的负数[8-10]，见式（1）。

其中，t表示时间，w(y)表示f(t)的概率分布函数；y表示f(t)的幅度；ymax和ymin分别表示f(t)的最大值和最小值；HC为熵值，对数以2 为底，单位为比特。

1.2 噪声辅助互相关算法

在获得的猪肝组织背散射信号中，会存在周围组织以及系统带来的噪声，而噪声会影响原始超声数据的分布。因此，需要对噪声进行处理。Tsui 等[14-15]提出噪声辅助互相关算法对噪声进行处理并应用于Nakagami 成像中，证明了可以消除噪声的影响。本文以此为基础对信号进行处理。在背散射信号中随机加入两组白噪声，得到两帧添加白噪声的射频信号，通过滑动窗口法计算两帧射频信号的相关系数，见式（2）。

式中，S1[k]和S2[k]表示两帧添加白噪声的射频信号；k表示样本数；n表示窗口数；N表示样本总数；Lw表示窗口内的样本数；L0表示范围采样数；Δ=Lw-L0；和分别表示S1和S2在窗口n下的平均值。

对于超声数据而言，加入的随机白噪声很小，对射频信号的影响也很小。这就使得两个噪声射频信号在散射介质内的波形几乎相同，式（2）中的S1和S2接近，r趋向于1；而在消声区域，由于噪声的随机性，两个射频信号的波形将会不同，令r减小。通过设置一定的阈值，使得小于阈值的区域振幅为0，可以达到消除噪声的目的。本实验阈值设置为0.8 可以达到较好效果。

1.3 实验设备与数据采集

微波消融实验设备包括超声信号采集装置（型号：Terason T3000，美国Terason 公司制造），线性超声探头（型号：12L5A，中心频率：7.5 MHz，通道数：256），固定超声探头的支架，微波消融仪（型号：KY-2000，南京康友公司研制），水冷式消融针（型号：EN868-5），自制消融盒子（尺寸：6 cm×6 cm×6 cm）等。实物图如图1 所示。

图1 微波消融实验设备

购买新鲜的猪肝组织，将其放入0.9%氯化钠溶液中，静置2 min 以达到去气的目的。然后将猪肝切割为合适大小并放入自制消融盒子中，在盒子中加满0.9%氯化钠溶液，使超声探头与猪肝组织充分接触，也能保护探头不会因加热过程中温度升高而受损。将微波消融针通过盒子中心的圆孔插入猪肝组织中，设置微波消融仪参数（加热功率P=80 W，加热时间t=60 s），消融结束获取超声背散射回波信号。共进行了15 例离体猪肝微波消融实验。

采集热消融结束瞬间猪肝组织超声背散射信号，微波热消融结束时，将猪肝组织沿超声探头扫描平面切开，测量并记录肝脏组织剖面中凝固区的长轴a和短轴b，利用公式（3）计算实际凝固区面积S1作为金标准；利用信息熵成像算法检测凝固区，利用多项式拟合技术对凝固区面积进行预测，得到预测值S2。根据公式（4）计算凝固区检测精度。

1.4 成像

获取超声背散射信号后，利用希尔伯特变换得到包络信号，对包络信号进行对数压缩和扫描变换，得到B 模式图像。利用噪声辅助算法对未压缩的包络信号进行处理，再通过滑动窗口技术得到包络数据的熵值矩阵。步骤如下：利用滑动窗口选取包络数据，采用直方图估计法得到数据的概率密度函数w(y)，再利用公式（1）计算熵值；将得到的熵值作为滑动窗口新的像素值，根据窗口重叠率（本文采用50%的窗口重叠率）在整幅图像上移动，重复第一步，进而得到整幅图像的熵参数矩阵，经过颜色映射得到信息熵成像。

2 结果

2.1 信息熵成像分析

对1 例消融结束的猪肝超声背散射信号进行B 超成像和信息熵成像，见图2。

图2 猪肝超声背散射信号成像

由于背景噪声的干扰，在图2b 信息熵成像中使得凝固区与周围组织的区分并不明显，不能准确地检测凝固区。因此，利用噪声辅助互相关算法对信号进行处理。图3 显示了经噪声辅助互相关算法处理后的超声背散射信号信息熵成像。

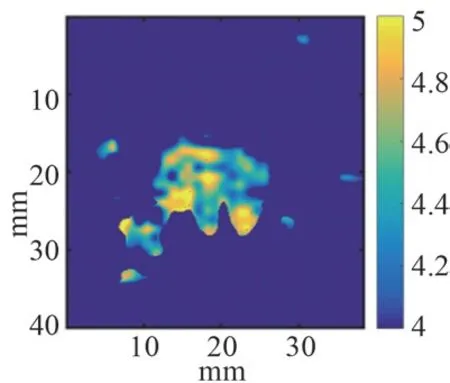
图3 基于噪声辅助互相关算法的信息熵成像

对比图2b 和图3 可以看出，经处理后的信号，噪声可以得到有效抑制。在熵成像图中，凝固区与周围组织的差异比较明显，可以检测凝固区的变化。

为了能对凝固区的大小有更精确的表示，采用多项式拟合技术[16]对凝固区进行定量估计。通过实验发现，多项式阶数为6、拟合阈值为0.5 时，经拟合得到的面积与实际面积相接近，图4a 和图4b 分别表示了多项式拟合图像和实际猪肝组织剖面图像。

图4 多项式拟合图像（a）和猪肝组织刨面（b）

在信息熵的计算中采用直方图估计法，直方图估计中区间即bins 的大小与估计的效果是密切相连的。因此，通过实验验证了不同bins 数量下信息熵成像对凝固区检测的影响。图5 给出了不同bins 数量下的信息熵成像图和多项式拟合图像。多项式拟合下的面积分别为149.4940、154.5129、156.3292 mm2。

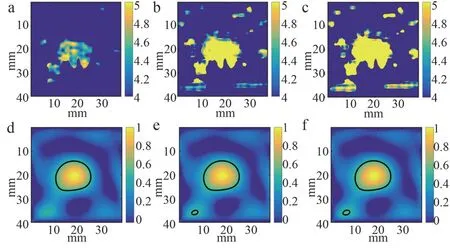
图5 不同bins数量下的成像图

2.2 凝固区检测结果验证

对超声背散射信息熵成像检测凝固区方法进行验证，15 例猪肝组织凝固区检测结果如表1 所示，对比金标准和预测值可以看出，超声信息熵成像估算出的凝固区面积总体偏小。通过统计15 例数据的精确度，可以得到其平均精度为87.42%。

表1 凝固区检测结果（P=80 W、t=60 s）

3 讨论

本文利用信息熵作为组织参数并进行成像，用于检测热消融凝固区。通过15 例离体猪肝微波消融实验对算法进行验证。

信息熵作为信号不确定性的度量，熵值越大，表明信号不确定性越大。对于生物组织，信息熵可以描述其内部散射子的混乱程度；而且，信息熵是关于概率密度的函数，与统计分布有关，从某一方面反映了信息熵的物理意义。

现有的凝固区检测技术主要包括两大类：超声弹性成像技术和定量超声技术。超声弹性成像的原理是凝固区的组织硬度高于未受热区域[17-18]。但因其受气泡影响较大，不适合在加热过程中对凝固区进行检测。定量超声通过对组织中的散射子进行估算并成像，如Nakagami 成像[3-4]、零差K 成像[5-6]、超声衰减系数成像[19]、超声回波去相关成像[20]等。Nakagami 成像的Nakagami 参数m 为形状参数，与组织散射子的浓度或排列有关，可以反映散射子浓度的变化。零差K 成像利用有效散射子数目参数a 或m 来检测凝固区的变化。但其大部分都属于基于模型的统计成像方法，需要背散射信号符合所使用的统计分布，具有一定的局限性。相比较而言，信息熵是一种基于非模型的参数统计方法，不需要特定的数据分布。与其他的方法相比，信息熵在凝固区的检测精度上相差不大，但是其更灵活的成像方式，可以成为一种新的凝固区检测方法。

在信息熵的估算中，直方图的bins 数量会对熵值产生影响。如果区域选择过大，会导致最终估计出来的概率密度函数非常粗糙；如果区域的选择过小，可能会导致有些区域内根本没有样本或者样本非常少，这样会导致估计出来的概率密度函数很不连续。从图5 可以看到，随着bins数量的增加，凝固区的亮度随之增加；但随着bins 数量的增加，在凝固区周围会出现噪声的影响，会影响多项式拟合的面积。因此，选择合适的bins 数量对于凝固区的检测也是比较重要的。

本文只对离体猪肝进行实验，验证了算法的有效性，未来需要通过在体实验验证方法的准确性；本文仅在P=80 W，t=60 s 下进行实验，未来可以依据临床参数，设置不同的参数进行实验；可以考虑不同超声参数间的融合来检测凝固区，提高算法的精度。

4 结论

超声背散射信息熵成像可以检测微波消融凝固区，通过15 例离体猪肝实验验证，其检测精度为87.42%，可作为一种新的凝固区检测方法，对肝肿瘤微波消融凝固区检测具有指导意义。