电阻抗断层成像技术重建方法对比研究

孔令睿，宾光宇，吴水才

北京工业大学 环境与生命学部，北京 100124

引言

电阻抗成像（Electrical Impedance Tomography，EIT）是一种根据场域内阻抗分布变化重建场域内部图像的成像技术。在测量场周围设置一定数量的电极，通过对其中一组电极施加安全范围内的激励电流或激励电压信号，测量其余电极的电位分布，将测量得到的电位分布重建为电导率分布的图像。

由于人体在呼吸时肺部的通气量会产生明显改变，吸入的空气不导电，导致空气的电导率与肺部组织的电导率有明显差异，肺部区域的阻抗分布也会发生显著变化[1-2]，所以EIT 技术能够有效描绘肺部通气区域的动态变化[3]，可以应用于肺部呼吸功能的检查，这也是目前EIT 技术主要应用的领域[4-6]。EIT 技术还具有对人体无害、无创、成像速度快、成本低、可多次重复测量等优点，在临床监测领域具有广阔的应用前景[7-8]。

EIT 成像技术中通常会遇到传统算法计算复杂、噪声环境中重建图像质量差的问题[9]，临床应用中EIT 成像技术会面临更多干扰，如被测者动作导致较大的噪声、电极接触面的阻抗变化、计算量大导致成像速度慢等都会对重建图像质量产生影响[10]，所以在临床应用中需要对传统算法进行优化。2009 年，Adler 等[11]提出一种依靠数据驱动的线性重建方法—GREIT，并在肺部阻抗成像中得到应用。2012 年，Borsic 等[12]设计了一个使用L1 范数的原始对偶内点法框架用于EIT 图像重建，证明可以有效处理数据异常值，对带有噪声的数据有更好的重建效果。2014 年，Grychtol 等[13]采用8 只麻醉猪进行实验，通过给猪肺插管连接至呼吸机控制通气量，在不同通气效果下进行EIT的数据测量，使用反投影（Back Projection，BP）算法、GREIT 算法、截断奇异值分解法、一步高斯牛顿法及其几种变体等十二种2D 重建方法对测量数据进行重建，比较各算法重建效果。比较结果表明，十二种方法中的先进优化算法比传统算法效果更好，但传统算法中的BP 算法在实时成像效果中表现较好。

交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）是一种求解具有可分离的凸优化问题的计算框架，其处理速度快、收敛性能好[14]，可以快速并准确地求解EIT 逆问题。本研究设计了三组实验，选取了EIT 传统算法牛顿法中的一步高斯牛顿法[15-16]，适用于实时成像的BP 算法[17-18]以及新式优化算法GREIT 算法[11]与ADMM 算法做图像重建。实验建立仿真模型，在模型内部的不同位置设置圆形目标，添加一定的高斯噪声，将4 种算法重建出的图像进行直观对比，并采用5 种评价参数[11]对重建结果的质量进行量化评价。根据重建结果图像和评价参数对比验证ADMM 算法的有效性，并分析几种算法的优劣性。

1 电阻抗成像数学模型

EIT 问题的求解分为求解正问题及逆问题两部分。正问题是根据麦克斯韦方程组建立数学模型，采用有限元法在已知场域内电导率分布和边界激励信号的情况下，求解电势分布近似解[19]。逆问题则是根据测得的电压以及已知的边界激励信号求解场域内阻抗分布。对于EIT 问题，边界处的电压测量值与阻抗分布变化的对应数学模型如式（1）所示。

其中，U表示边界处电极上测量的电压数据；S表示正问题求得的敏感系数矩阵；σ表示阻抗分布。

逆问题求解时方程的解可表现为σ=S-1U，由于S不是一个方阵，方程无法直接求逆，由电磁场的软场特性也可得知测量电压与电导率分布存在非线性关系，且求解方程存在病态性，因为在实际测量中边界电压是在离散点上采样，电极数目有限，由边界电极获得的信息不足以决定目标内部的阻抗分布，方程为欠定方程，存在无穷多组解，求得的解不唯一且存在不确定性。所以EIT 逆问题是一个高度非线性病态问题，求解具有一定的难度，逆问题的求解也就是图像重建方法也成了多数研究的重点。

由于逆问题是一种非线性问题，传统的EIT 成像算法通常是将逆问题近似为一种线性问题，构造目标函数，见式（2）。逆问题求解就是求解该目标方程的最优解。

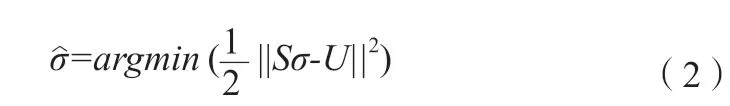
2 电阻抗成像重建方法

2.1 BP算法

BP 算法[17]是一种基于等位线间电位差变化投影的图像重建方法。算法的基本原理是在电导率变化较小时，在两条相邻等位线间的投影区域内将等位线间的阻抗分布和电势分布的变化等价为线性关系，利用两个时刻之间的测量电压数据的差值，进行归一化然后再沿等位线作反投影，再将投影区域内的结果叠加起来，得到阻抗值变化的结果，就可以作出差分重建图像。BP 算法的计算公式如式（3）所示。

其中，A为阻抗分布与电势分布线性关系系数；ΔU为电势分布变化；Δσ为阻抗分布变化；j为测量电极编号。

因为在差分计算的过程中测量数据里的部分噪声和误差可以消减一部分，所以BP 算法的抗干扰性较好。BP 算法还有重建算法易实现、成像速度快、便于实时成像的优点。但BP 算法的成像精度不够理想，达不到临床应用的精度要求。

2.2 一步高斯牛顿法

一步高斯牛顿法[15]是一种基于牛顿迭代法衍生的一步快速算法。一步高斯牛顿法的基本思想原理是在假定电导率分布发生一个较小的扰动的条件下，认为作差分求解后求得的电导率分布与真实的电导率分布之间的误差极小，可以忽略，因为动态成像过程中主要是获得两个时刻间数据的差值，所以放弃牛顿迭代法中的迭代过程，只取一步计算。其目标函数如式（4）所示。

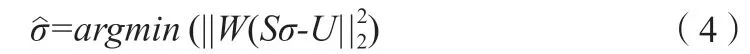
其中，W为测量电压值的协方差矩阵。

为了克服病态性问题，需要在目标函数中引入正则化项，使目标函数的求解有约束后能够变得收敛稳定。加入正则化项的目标函数表现形式如式（5）所示。

其中，R为正则化矩阵；λ 为正则化参数，λ 通常根据经验定义。

对这种形式的目标函数求解用最小二乘法，目标函数最小二乘解的形式如式（6）所示。

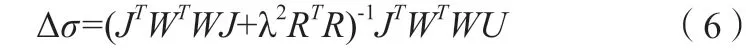
其中，Δσ为两个时刻前后电导率变化；J为Jacobian矩阵。

2.3 GREIT算法

GREIT 算法是一种依靠数据驱动的重建算法[11]。其目标函数如式（7）所示。

其中，σ为阻抗分布；U为电势分布；R为重建矩阵。

GREIT 算法的基本思想是将一系列的仿真数据作为训练目标进行训练后，得到使重建图像误差最小的重建矩阵R，再对其他数据进行重建时，直接利用重建矩阵即可得到阻抗分布。求解最优重建矩阵的计算公式如式（8）所示。

其中，ε为图像重建误差；k为训练样本数；w为加权矩阵，是每一个训练目标在计算重建矩阵中的权重。

对公式（8）进行求导可得公式如式（9）所示。

由公式（9）可得重建矩阵R如式（10）所示。

2.4 ADMM算法

ADMM 算法是一种将对偶上升法的可分解性与增广拉格朗日乘子法的收敛性结合起来的算法，在求解分布式凸优化问题中得到广泛应用。在EIT 应用中可以用来求解式（11）：

其中，J为Jacobian 矩阵；F为正则化矩阵；λ 为正则化参数。

分3 步做迭代求解，见式（12）～（14）。

其中，公式（13）为2 范数求解问题，求解可得式（15）。

公式（14）为1 范数正则问题，可以通过软阈值公式进行求解得式（16）。

其中，Shrink称为软阈值算子，其含义如式（17）所示。

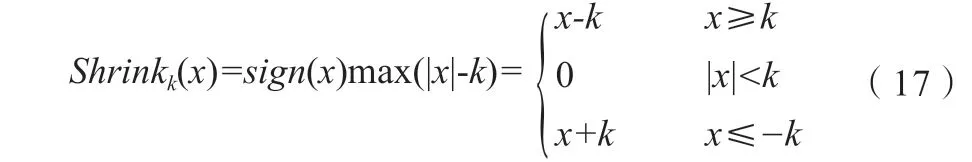
软阈值公式也称软阈值收缩公式，因求解的过程可以看作收缩的过程。这种求解思路在很多其他类似的问题上（如硬阈值、TV 正则化项等）都得到应用。

3 实验设计

为了全面对比不同算法的重建性能，共设计了3 组实验，实验基于Matlab R2018a 版本和EIDORS 软件包完成。第一组实验是在普通圆场域中的不同位置放置电导率相同、半径相同的单目标，分别在理想环境和噪声环境下用不同算法进行重建，对比不同算法在场域不同位置处的目标的重建能力。第二组实验是在普通圆场域中的不同位置放置电导率不同、半径不同的双目标，同样分别在理想环境和噪声环境下进行重建，对比不同算法对双目标物体的重建能力。第三组实验是选取胸腔轮廓模型，将成人在呼吸过程中的测量数据进行重建，对比不同算法在实际应用中的性能。

第一组、第二组实验使用的都是半径为1 的二维圆形有限元模型（图1），在边界周围设有16 个电极，采取相邻激励-相邻测量模式，施加幅值为1 mA 的电流，模型被划分为46194 个单元，背景电导率设置为1。然后使用软件包中的公式来计算正问题，选择一对电极对作为电流的注入电极，随后测量剩余电极对之间的电压。最终获得208（16×13）个边界电压值。

图1 圆形二维有限元模型

第一组实验在沿圆域水平半径上0～0.9 区域内以平均间隔取50 个点作为圆心，依次放置半径为0.05、电导率为2的目标物体。分别使用GREIT 算法、BP 算法、一步高斯牛顿法、ADMM 算法进行图像重建。第二组实验设计了双目标仿真数据重建，来比较不同数目的目标物体的重建效果。在简单圆形场域内随机生成两个大小不同、电导率不同的目标。目标的半径大小和位置都是随机的，半径的取值范围为0.05～0.1，其中一个目标的电导率设置为10，另一个目标电导率设置为0.1。两个目标的位置设置不会使两个目标完全重合，但可能会有一部分的重叠。第三组实验设计使用模拟肺部轮廓的有限元模型对成人肺部呼吸实际测量数据进行重建，来验证几种重建方法在实际应用中的重建效果。数据来自EIDORS 软件包，受试者采取仰卧位，0 号电极放置在受试者背部中心位置，采取相邻激励-相邻测量模式，在受试者正常呼吸时以7 帧/s 的速度采集数据，这些数据体现了一次完整的呼吸过程，共有34 组。

3.1 评价参数

研究选取了振幅响应（Amplitude Response，AR）、位置误差（Position Error，PE）、振铃（Ringing，RNG）、分辨率（Resolution，RES）、形状变形（Shape Deformation，SD）5 项评价参数对重建算法进行量化的评价。

3.1.1 AR

AR 反映了重建图像成像的稳定性，其公式如式（18）所示。

其中，k为一幅图像像素的个数，x为图像像素，Vt为目标的体积，σt为目标的阻抗值，σr为背景区域的阻抗值，Δσ=σt-σr。

对于AR 的评价标准，在整个场域内任何位置的目标的AR 越恒定，说明重建效果越好。恒定的AR 是评价参数中最重要的一项，因为当AR 不恒定时，说明目标处于场域内不同位置时将对图像产生不同的贡献，将会难以评价重建图像。

3.1.2 PE

PE 反映了重建图像目标位置与实际目标位置的误差。其公式如式（19）所示。

其中，rt为重建图像中目标到场域重心的距离；rq为xq到场域重心的距离；xq为所有大于1/4 最大振幅的图像像素，其计算公式如式（20）所示。

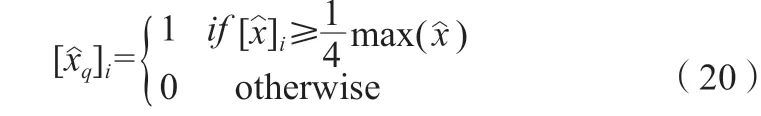
PE 的值为正时，说明重建图像目标位置对比实际目标位置更靠近中心位置。

对于PE 的评价标准，PE 越小就是误差越小，说明重建图像越准确；并且在位于不同径向位置目标的PE 越稳定说明重建图像效果越好。

3.1.3 RNG

RNG 是测量重建图像中圆C外相反符号的图像振幅与圆C内图像振幅之比。其公式如式（21）所示。

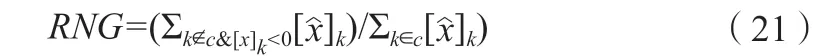
其中，圆C为以xq的重心为圆心的圆。对于RNG 的评价标准，RNG 应该尽可能小且均匀，过冲会导致图像产生不正确的解释。

3.1.4 RES

RES 反映了重建图像中目标的大小，与点扩散函数、的大小相同，其公式如式（22）所示。

其中，Aq=Σk[xq]k，为圆C内像素值的和；AO为重建图像的所有像素叠加。

对于RES 的评价标准，RES 应该尽可能小且均匀，才能更准确地表示目标阻抗分布的形状。如果不同位置的目标RES 不均匀，会导致面积较大的目标重建位置不准确。

3.1.5 SD

SD 是测量重建图像目标的伪影，即重建后的图像中的目标像素xq不在圆C内的部分占比，其公式如式（23）所示。

对于SD 的评价标准，SD 应该尽可能小且均匀，SD越大说明重建目标位置与原始目标位置误差越大，说明重建目标伪影大，结果不准确，解释重建图像时可能会导致解释错误。

3.2 实验结果

程序运行的计算机为荣耀MagicBook Pro，运行内存16.0 GB，CPU 为Intel（R）Core（TM）i5-8265U@1.60 GHz，显卡为Nvidia GeForce MX250。由于GREIT 方法需要先使用仿真数据训练模型，再用训练好的模型进行图像重建，但每个模型只需训练一次，所以对模型的训练时间单独计算，模型训练大约需要21.02 s。每种方法的重建时间如表1 所示。

表1 图像重建方法运行时间比较

从50 个数据中取选10 个进行重建图像结果展示，结果如图2 所示。其中ADMM 算法采用的是L1 正则化，一步高斯牛顿法采用的是L2 正则化。可以由图2 看出4 种算法在无噪声环境中都是在场域中心位置的伪影较大，在边缘位置的伪影较小。

图2 单目标无噪声数据图像重建结果

为了更贴近实际情况环境，测试本文重建方法的抗干扰性，实验在仿真数据中加入12 dB 高斯噪声，使用带有噪声干扰的模拟电位进行图像重建。重建结果如图3 所示。由图3 可知，相比其他算法，ADMM 算法在加入噪声后重建结果总体看来受到的扰动最小，中心区域的目标图像扰动较大，目标的形变比较大，而边缘区域的重建效果较好，几乎与无噪声环境中的重建效果相同。而一步高斯牛顿法、BP 算法和GREIT 算法在噪声环境中的目标图像受到噪声的影响都比较大，抗干扰能力较差。

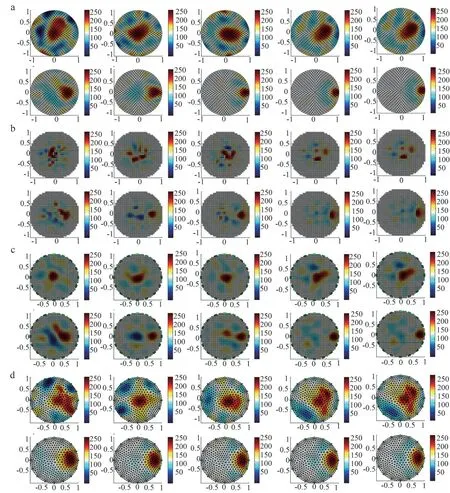
图3 单目标12 dB噪声数据图像重建结果

各重建方法对50 个数据的重建评价参数的对比结果如表2～3 所示。由表2～3 的评价参数对比可看出，在无噪声环境中GREIT 算法的各评价参数表现相对较优，AR 最接近于1，所有参数都相对较小而且较均匀稳定。而对噪声数据的重建，ADMM 算法的PE、RNG 和SD 的值都相对较小，说明ADMM 算法相比其他算法对加入噪声的数据重建结果更准确，具有明显的抗噪声干扰优势。

根据表2 的评价指标，GREIT 算法在无噪声时RNG、RES 和SD 的均值为0.168、0.281、0.067，均值都是最小的，并且方差为0.005、0.001、0.001，方差较小，变化幅度最稳定，AR 为1.095±0.025 也较为接近1，所以在无噪声情况下GREIT 算法的表现较好。根据表3 的评价指标，ADMM 算法在加入12 dB 噪声后PE、RNG 和SD 的均值为0.018、0.405、0.202，相比其他算法最小，方差为0.013、0.066、0.009，相比其他算法是最小的，变化幅度最稳定，所以ADMM 算法相比其他算法对加入噪声的数据重建结果更准确。对比表2 和表3 也可看出，在加入12 dB 噪声后，ADMM 算法的各评价指标相比无噪声时的评价指标变化最小，变化最大的参数是AR，在加入噪声后均值降低了0.242，其他算法的参数均值变化最大值约为0.8，所以ADMM 算法具有明显的抗噪声干扰优势。

表2 无噪声数据重建图像评价参数（±s）

表2 无噪声数据重建图像评价参数（±s）

方法ARPERNGRESSD一步高斯牛顿法0.732±0.0690.012±0.0010.285±0.0370.356±0.0080.089±0.002 BP算法0.801±0.012-0.009±0.0010.224±0.0690.283±0.0010.082±0.003 GREIT算法1.095±0.0250.019±0.00020.168±0.0050.281±0.0010.067±0.001 ADMM算法0.923±0.0340.010±0.0040.250±0.0030.414±0.0010.111±0.015

表3 加入12 dB噪声数据重建图像评价参数（±s）

表3 加入12 dB噪声数据重建图像评价参数（±s）

方法ARPERNGRESSD一步高斯牛顿法0.710±0.1200.052±0.0070.627±0.0870.412±0.0200.258±0.015 BP算法1.035±0.0390.168±0.0171.031±0.1240.287±0.0020.536±0.026 GREIT算法1.020±0.0330.203±0.0260.936±0.1620.346±0.0030.512±0.039 ADMM算法0.681±0.0870.018±0.0130.405±0.0660.467±0.0130.202±0.009

除了测试重建算法的抗噪能力，还需要对重建算法的泛化能力进行评估，因此第二组实验设置了两个位置随机的重建目标，两个目标的电导率分别设置为0.1 S/m 和10 S/m，第二组实验重建结果如图4 所示。由图4 可以看出，双目标重建结果中BP 算法和GREIT 算法可以将选展示结果中的各个位置的目标全部明确重建出来，一步高斯牛顿法和ADMM 法某些部位的重建结果比较模糊。

图4 双目标无噪声数据图像重建结果

在双目标数据中同样加入12 dB 高斯噪声，测试双目标条件下各重建算法的抗干扰性，重建结果如图5 所示。由图5 可以看出，双目标重建在加入噪声后一步高斯牛顿法、BP 算法、GREIT 算法都受到了噪声的干扰，重建目标的振铃现象增多，目标形变增多，而ADMM 算法受到噪声干扰最小。

图5 双目标12 dB噪声数据图像重建结果

共生成双目标数据50 个，50 个数据重建结果的PE、RNG、RES 和SD 的对比结果如表4～5 所示（AR 仅可对单目标数据重建结果进行计算）。由表4～5 的评价参数对比可看出， ADMM 算法重建结果的位移误差都相对较小，无噪声与加入噪声的重建结果评价参数变化较小，说明ADMM算法有一定抗噪声干扰能力。

根据表4 的评价指标，GREIT 算法在无噪声时RNG、RES 和SD 的均值与方差的值都相对较小，重建图像的伪影较少，GREIT 算法对无噪声数据的重建效果较好。根据表5 的评价指标，ADMM 算法在加入12dB 噪声后PE 的均值和方差相比其他算法最小，加入噪声后重建目标的位置是最准确的，而振铃和形变的表现较差，说明ADMM算法的泛化能力不足。对比表4 和表5 参数同样可看出，在加入12 dB 噪声后，ADMM 算法的各评价指标相比无噪声时的评价指标同样变化最小，所以可以再次验证ADMM算法较强的抗干扰性能。

表4 无噪声双目标数据重建图像评价参数（±s）

表4 无噪声双目标数据重建图像评价参数（±s）

方法PERNGRESSD一步高斯牛顿法0.103±0.0291.358±0.8360.341±0.0100.193±0.017 BP算法0.102±0.0231.473±1.3910.275±0.0020.148±0.020 GREIT0.150±0.0161.258±1.0010.28600.111±0.003 ADMM0.103±0.0252.120±3.4300.365±0.0030.189±0.029

表5 12 dB噪声双目标数据重建图像评价参数（±s）

表5 12 dB噪声双目标数据重建图像评价参数（±s）

方法PERNGRESSD一步高斯牛顿法0.105±0.0291.365±0.8220.343±0.0100.195±0.018 BP算法0.112±0.0241.552±1.4690.278±0.0020.171±0.021 GREIT0.198±0.0231.269±0.6950.304±0.0010.200±0.020 ADMM0.107±0.0242.090±3.0380.365±0.0040.198±0.033

为了验证几种重建算法在对实测数据的重建中是否有效，采用了在成人呼吸过程中测量的肺部电压数据进行重建，选取了一段完整的呼吸过程，第三组实验重建结果如图6 所示。由图6 可知， GREIT 与ADMM 算法的重建效果较好，成像目标的位置和大小的误差都相对较小，重建图像内容解释准确，重建目标边界更清晰。

4 讨论

在近几年的相关研究中[20-22]，在比较算法性能时大多数研究仅采用了仿真数据进行实验，一些采用实测数据的实验也是以模拟环境进行实验[20]，为了能够更准确验证重建算法的实用性，本文采用了成人呼吸过程中对肺部的测量电压进行重建。由图6 可得，对于实测数据的重建效果，GREIT 算法的重建结果中肺部轮廓较清晰，伪影少，ADMM 算法对肺部位置和大小的重建都比较准确，两种算法都可以观察到呼吸过程中肺部通气的变化。

图6 实测数据图像重建结果

但这两种方法还存在一些需要进一步研究和解决的问题。由于ADMM 算法需要进行迭代运算，相比其他算法运行速度慢了很多。达到最好的重建效果时，需要迭代的次数更多，用时会更长；并且目前实验都是基于二维有限元模型进行重建，如果应用于三维模型中，有限元划分更多导致计算量会更大。而GREIT 算法无法很好地抑制噪声的干扰。在保持算法精度的前提下，进一步提升ADMM 算法的运行速度和GREIT 算法的抗噪性能是需要继续研究改进的问题。

5 结论

本文基于圆形模型和胸腔轮廓模型比较了ADMM 算法、GREIT 算法、一步高斯牛顿法和BP 算法的重建性能，设计了三组实验。根据实验结果可知，ADMM 算法的重建性能表现较为优秀，对单目标和多目标物体的面积与位置的重建都比较准确，重建图像精度高，最突出的特点是抗干扰性能较好，但是重建目标的边界不够清晰；而GREIT算法在无噪声的情况下重建效果比较好，重建目标的均匀性好，并且可以保留边界。对于肺部功能成像应用来说，这两种方法都可以做到有效辅助医护人员对肺部通气情况进行判断，具有一定的临床应用价值。