基础模拟方法对连续梁桥抗震性能的影响
2022-08-03马辉刘斌
马辉 刘斌
(1.永平县交通运输局 永平县农村公路建设管理站,云南 大理 672600;2.云南交通职业技术学院交通勘察设计研究院,云南 昆明 650501)
地震是一种常见自然灾害现象,能够对人类活动产生巨大影响[1-2]。人类历史上曾经出现过多次造成严重损失的地震,例如2008年汶川8.0级地震,直接造成8万多人伤亡,直接损失达到8451亿元;1995年位于大阪与神户之间的7.2级阪神地震造成城市交通系统瘫痪,大量公路桥梁受损。
桥梁是交通系统的重要组成部分。如在地震发生时出现严重损伤导致交通瘫痪,不仅会造成较大经济损失,还会阻碍救援进度,对人们的生命财产安全造成巨大威胁,因此需在设计阶段重点关注桥梁的抗震性能[3-4]。连续梁桥是一种量大面广的桥梁形式,具有行车舒适、构造简单、力学性能明确等优势,因此连续梁桥抗震性能的准确计算至关重要。目前桥梁结构抗震分析的主流软件为Midas Civil,规范中通常将桥梁下部结构简化为主梁上的边界条件以简化模型,提升计算效率[5-6]。但这种简化方式偏保守地考虑了桥梁下部结构的边界约束,实际上与桥梁下部结构接触的土体刚度有限,在地震作用下并不能完全抵御下部结构的变形。
数值模型的建立方式、与实际桥梁形式的匹配程度均对计算结果的准确性有较大影响。为研究基础模拟方法对连续梁桥抗震性能的影响,本文以某4×30m跨径预应力混凝土连续梁桥为依托,建立两种基础模拟方法的Midas Civil有限元模型,开展地震作用下的动力计算,分析了桥梁跨中截面的速度、加速度、位移时程结果。
一、工程概况
以某4×30m跨径预应力混凝土连续梁桥为研究对象,桥梁纵断面如图1所示。桥梁纵向采用4根主梁,为保证主梁横向协同受力,纵桥向间隔7.5m布置横向联系。桥梁横向宽度为12m,设计行车速度40km/h。采用高度2.2m预制T梁,中跨梁与边跨梁的宽度分别为2.5m与2m,各梁支座处腹板厚度为50cm,跨中腹板厚度为20cm。
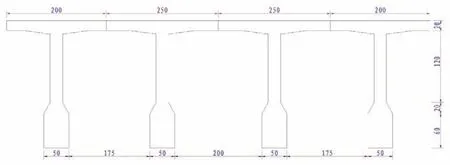
图1 桥梁断面图
该桥主要技术标准有,桥型为预应力混凝土T型简支梁桥;设计荷载为公路-Ⅱ级;设计洪水频率为1/100;设计行车速度为40km/h;地震动峰值加速度系数为0.05g,抗震按Ⅶ设防。
桥墩与桥台均由C30混凝土浇筑而成,主梁由C50混凝土、沥青混凝土与预应力钢绞线组成,沥青混凝土主要用于桥面铺装,钢铰线公称直径为15.2mm,其松驰率为0.035,松驰系数为0.3。桥梁主要组成材料设计参数如表1所示。
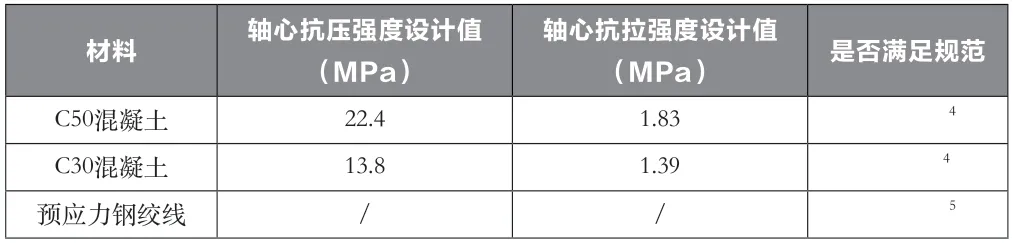
表1 材料参数
二、数值模型建立
(一)基础模型建立
采用Midas Civil建立4×30m跨径连续梁桥数值模型,主梁、横向联系等均采用梁单元,全桥可离散为1773个节点,2892个单元,数值模型建立结果如图2所示。

图2 数值模型建立结果
桥梁上的荷载如表2所示,模型中主要考虑了恒载、活载两种情况,其中恒载主要包括自重、预应力荷载,活载主要包括汽车荷载、整体温度变化、温度梯度变化。
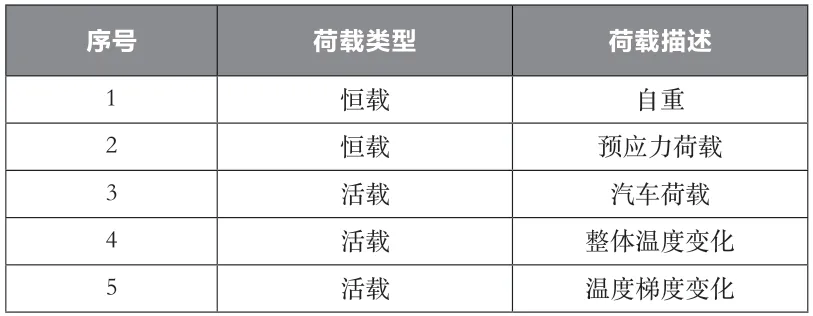
表2 桥梁上的荷载
传统有限元方法通常选择忽略桥梁下部结构的实体模型,简化下部结构为边界条件,桥梁边界条件如图3所示。
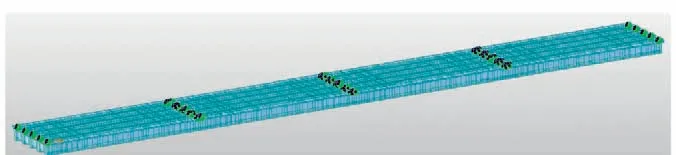
图3 桥梁边界条件
(二)桩基础的模拟
在桥梁有限元模型中考虑桩基础,首先采用梁单元建立桥梁下部结构模型,然后在模型底部加固节点,被土体包围的桥梁下部结构采用弹簧边界条件考虑土体对基础的作用。最后采用等代弹簧代替桩基础周围的土体作用。土弹簧刚度根据土层的m值计算,计算公式如式1所示。

如式1所示,a为土层厚度;b为桩的计算宽度;m为地基土的刚度系数;z为土层深度。
(三)地震波模拟
分析中所采用的地震波时程荷载如图4所示。荷载工况定义参数为,结束时间取52s、分析步长取2、输出时间步长取26、分析类型取非线性、分析方法采用直接积分法、时程分析类型采用线性瞬态、振型阻尼比取0.03。
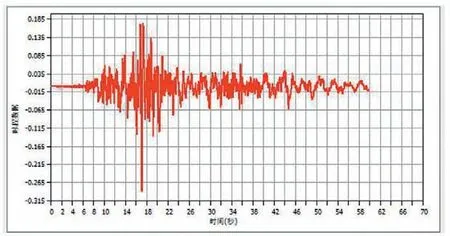
图4 地震波时程
三、结果分析
对该4×30m跨径桥梁展开静力分析及抗震分析。桥梁静力分析综合考虑桥梁所承受的恒载及活载,主要提取桥梁承载力极限状态的结构弯矩、变形、剪力等参数。承载力极限状态组合为1.2恒载+1.2预应力+1.4汽车荷载工况+1.4梯度降温。
(一)静力计算结果
计算分析该连续梁桥的静力,提取其在承载力极限状态下的变形及内力情况,结果如下:
1.边跨跨中的最大挠度值为+16.35mm,中间跨的最大挠度值为-3.36mm,产生差值的原因是边跨约束较弱而中跨约束较强;
2.最大负弯矩为-3165.85kN·m,最大正弯矩为+5031.75kN·m;
3.支座处的最大剪力为+1358.31kN,除支座截面以外梁体其余截面剪力在-1111.33kN~+1111.35kN之间波动;
4.边跨跨中截面下翼缘应力值为-14.9MPa,中跨跨中截面下翼缘应力值为-10.76MPa,边跨支座截面下翼缘应力值为+8MPa,中跨支座截面下翼缘应力值为3.84MPa。
(二)影响因素分析
初始组:考虑土体弹簧单元模拟桥梁下部结构基础的模型;对照组:桥梁下部结构简化为梁体上的边界条件的模型。分析初始组和对照组的动力,提取梁体跨中截面速度、加速度、位移时程曲线结果如图5所示,并得到以下结论:
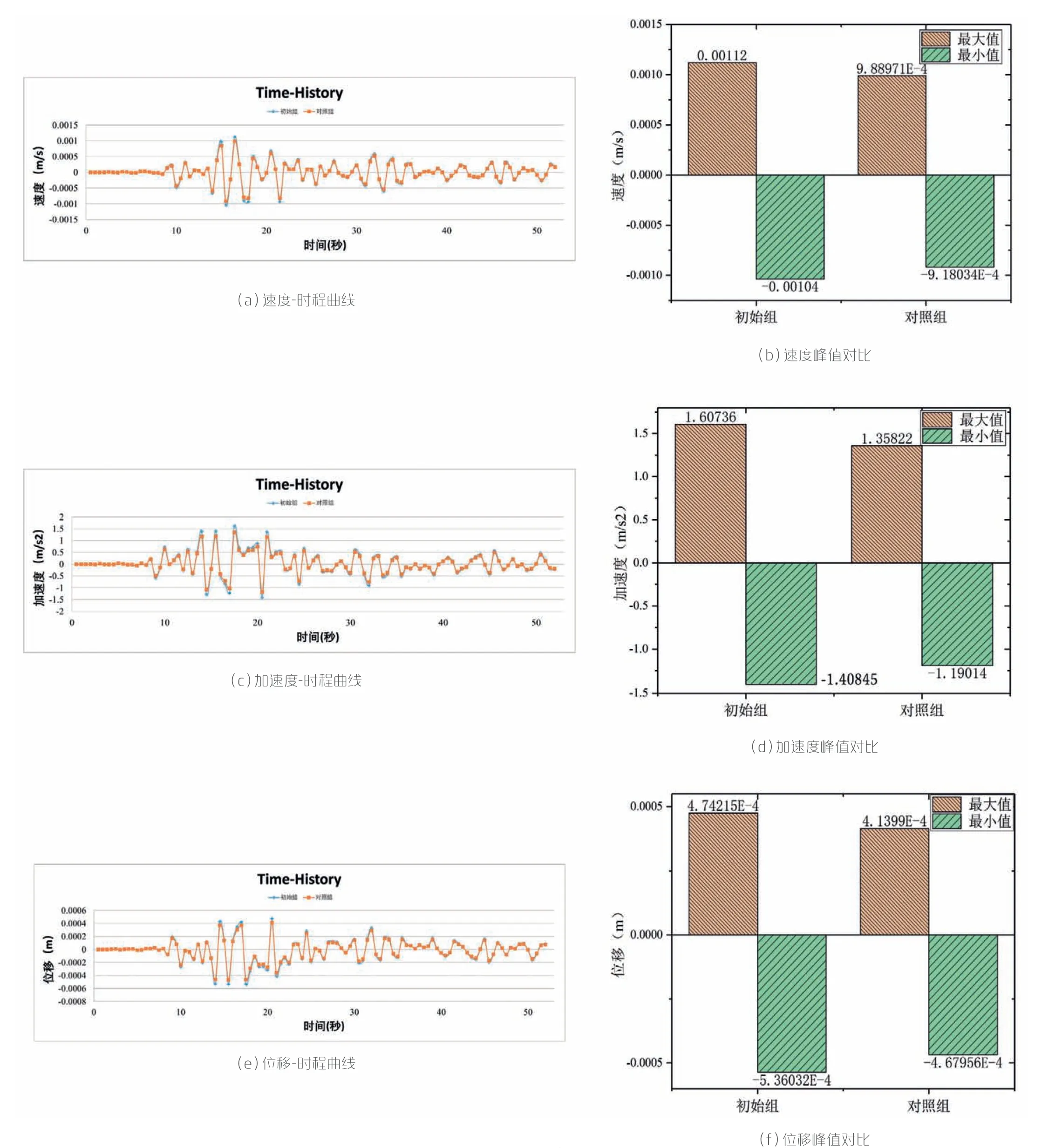
图5 连续梁桥动力计算结果
1.跨中截面速度、加速度、位移时程曲线结果显示在0s~10s、25s~50s之间,初始组、对照组间的差异不大,在10s~25s之间具有显著差异且对照组数值较小。这说明当在有限元模型中考虑桥梁下部结构的土体弹簧刚度后,桥梁结构整体约束减弱,桥梁在地震荷载作用下的力学响应增强。
2.初始组的速度-时程曲线的最大值与最小值分别为0.00112m/s、-0.00104m/s,对照组的速度-时程曲线的最大值与最小值分别为0.000989m/s、-0.000918m/s,当模型中考虑基础作用后速度峰值可降低11.6%。
3.初始组的加速度-时程曲线的最大值与最小值分别为1.60736m/s2、-1.40846m/s2,对照组的加速度-时程曲线的最大值与最小值分别为1.35822m/s2、-1.19014m/s2,当模型中考虑基础作用后加速度峰值可降低15.5%。
4.初始组的位移-时程曲线的最大值与最小值分别为0.0004742m、-0.000536m,对照组的位移-时程曲线的最大值与最小值分别为0.00041399m、-0.0004679m,当模型中考虑基础作用后位移峰值可降低12.7%。
四、结语
传统的将下部结构简化为边界条件的方式对于桥梁的抗震分析具有一定误差,本文选取某4×30m跨径预应力混凝土连续梁桥为研究对象,采用弹簧边界条件模拟土体与基础的接触,分析了不同建模方式对桥梁地震作用下结构响应的影响,得到以下结论:桥梁在承载力极限状态下边跨跨中、中跨跨中的最大挠度分别为+16.35mm、-3.36mm,最大负弯矩、正弯矩分别为-3165.85kN·m、+5031.75kN·m,支座处最大剪力为+1.358.31kN;跨中截面速度、加速度、位移时程曲线结果显示在0s~10s、25s~50s之间,初始组、对照组间的差异不大,在10s~25s之间具有显著的差异且对照组的数值较小;当模型中考虑基础作用后速度峰值降低11.6%、加速度峰值降低15.5%、位移峰值降低12.7%。
