基于慢特征分析的哈尔滨市气温预测研究

娄德君 潘昕浓 王冀 张雪梅 高振铎

(1.齐齐哈尔市气象局，黑龙江 齐齐哈尔 161006； 2.北京市气象服务中心，北京 100089；3.北京市气候中心，北京 100089； 4.哈尔滨市气象台，黑龙江 哈尔滨 150028 )

引言

对观测事实的研究表明，气候系统变化具有非平稳特征[1-3]，而外部强迫随时间的变化是导致非平稳行为产生的根本原因[4-5]。慢特征是指信号源中隐含的变化最缓慢的成分，能够表征信号源的固有属性[6]。研究表明，慢特征分析方法(Slow Feature Analysis，SFA) 是从已知的非平稳时间序列中提取缓变信息的有效方法，最近十余年，该方法在气象领域得到了初步成功的尝试[7-8]。根据Packard等[9]的状态空间重构理论以及Takens[10]的嵌入定理，王革丽等[11]在构建预测方程时考虑了外强迫信息，建立了外强迫因子参与在内的非平稳时间序列预测模型。试验结果表明，增加外强迫信息能够有效地改善模型预测精度。张彬[12]、陈潇潇等[13]分别对500 hPa月平均高度场和小时气溶胶浓度序列等进行了外强迫信息的提取，并将外强迫信息参与到预测建模中，结果均表明引入外强迫因子可以提高模型的预测技巧。

气温预测建模[14-15]时需考虑多种因素，而各因子之间存在着不同程度的相关，预测结果也会受到影响。以往研究表明，SFA方法对气候系统的慢变信号提取避免了常规方法主观选择因子的不足，客观性较强。因此，本文拟采用SFA方法对哈尔滨市气温序列进行研究，提取其慢特征信号，并构建包含慢特征信号的预测模型，旨在增进对黑龙江省气温变化规律的了解，并为黑龙江省气候预测提供一个新的思路。

1 资料与方法

1.1 资料来源

1961—2020年黑龙江省62个地面气象站逐月气温资料来自黑龙江省气候中心。相关分析表明黑龙江省气温具有较好的空间一致性，全年12个月各站点之间气温相关均较好，除个别站点在7月、8月、12月、5月与其余站相关略差外，大部分台站与其余站点气温的相关都通过了95%置信度检验，相关系数的大值区主要位于黑龙江省中部地区(图略)。哈尔滨市作为省会城市，且与全省其余61个台站气温的相关系数均通过了99%以上信度检验，具有代表性。因此，本文选取哈尔滨市为黑龙江省代表站，进行气温的慢特征信号提取及预测研究。文中气温均值取1981—2010年30 a平均。

1.2 研究方法

主要方法有慢特征分析(Slow Feature Analysis，SFA)、小波变换、相关分析等。

1.2.1 SFA方法简介

SFA方法是一种基于特征向量方法的无监督算法，基本思想是对向量矩阵进行特征值分解，最终得到函数最优解的集合[5,16]。慢特征分析方法步骤已有很多工作进行介绍[6,17-19]：

首先给定一个由非平稳时间序列重构的相空间X(t)，对其进行标准化处理

x(t)=[x1(t),x2(t),…,xn(t)]T

(1)

设置嵌入维数为m，时滞参数τ=1，对x(t)进行非线性扩展

(2)

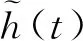
(3)

构建导函数空间，建立导函数的协方差矩阵并进行主成分分析，计算结果中选取最小特征值λj，对λj对应的特征向量进行标准化即得到权重向量w1,…,wj，输入函数变为gj(t)=wjz(t)。积分求得输出信号

yj(t)=rwjz(t)+c

(4)

其中r与c均为常数。选取最小的特征值时，积分后得到变化最慢的信号分量，即慢特征信号。

1.2.2 SFA方法提取非平稳系统中慢特征信号的能力

一维Logistic映射是一个非常简单的混沌映射，Logistic映射的动力学方程为

xn+1=μxn(1-xn)[20]

(5)

其中μ为控制参数，μ∈(0,4]，当μ∈[3.569945627,4]时，xn处于混沌区。

最大Lyapunov指数大于零通常作为系统存在混沌的判据。设定试验的控制参数μ∈[3,4]，步长为0.001，将μ代入到映射方程中迭代10000步(图略)可以看到，在μ取值区间内，存在最大Lyapunov指数大于零，因此系统处于混沌状态。

构造带有两个时变参数at、bt的Logistic映射

xt+1=atxt(bt-xt)t=1,2,…,N

(6)

令参数遵从下式

at=3.5+0.3cos (4πt/500)

(7)

bt=1.02+0.01cos(15πt/500)

(8)

at和bt分别代表慢变和快变信号，atbt在3.236—3.914范围内变化，表明序列在周期区和混沌区变化，即该序列是非平稳信号。

令初值x1=0.2，对式(6)迭代15000次，提取最后2000个数据作为试验时间序列{xt}，令嵌入维数m=11，时滞参数τ=1，对{xt} 进行慢特征分析，提取SFA信号{yt}，各信号轨线变化见图1。

图1 Logistic映射的原始外强迫信号{at}(a)、原始外强迫信号{bt}(b)、非平稳序列{xt}(c)和SFA信号{yt}(d)

{xt}为非平稳时间序列，SFA方法提取到的慢特征信号{yt}与两个原始真实外强迫信号均不相同，但其变化周期与慢变信号{at}的周期很相似， {yt}轨线上峰谷值附近呈锯齿状，可能是叠加了更小尺度的变化。采用Morlet小波变换方法[21]分析{yt}的时间平均功率谱(图2a)，由图可见{yt}功率谱有两个峰值，均通过95%置信度检验(图2a中虚线)。提取这两个峰值点所对应的尺度信号分量P1、P2，将标准化处理后的分量与两个原始外强迫信号{at}、{bt}比较，可以看到平移了约半个周期长度的P1分量与{at}拟合较好(图2b)，除两端受边界效应影响曲线振幅差异较大外，两曲线的中间时段拟合度较好，二者相关系数达到0.99。P2分量平移后与{bt}拟合度也较好(图2c)，二者相关系数为0.98。

图2 Logistic映射SFA信号的小波功率谱(a)、SFA信号慢变分量P1与原始外强迫信号{at}(b)、快变分量P2与原始外强迫信号{bt}(c)的比较

对Logistic映射构造的非平稳系统试验表明，SFA方法可以从序列中提取出与原始外强迫信号拟合较好的慢特征信号。利用小波分析方法可以分离出SFA信号中的显著周期分量，慢变和快变分量与原始外强迫信号都仅有位移和振幅差别，相关系数均超过0.98。

1.2.3 基于SFA方法的预测模型建立方法

王革丽等[11]在提取非平稳系统慢特征信号的基础上，结合状态空间重构理论、嵌入定理等，建立了非平稳气候预测模型：

{xi}、{Fi}为两个非平稳序列，{xi}是系统状态随时间的变化，{Fi}是{xi}的慢变信号。借助时滞参数τ将它们嵌入到m1+m2维的状态空间中，得到状态轨线

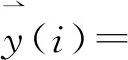
{xi,xi-k,…,xi-(m1-1)k;Fi,Fi-τ,…,Fi-(m2-1)k}i=1,2,…,N

(9)

式(9)中，m1为{xi}、m2为{Fi}的嵌入维数；N=n-(max(m1,m2)-1)k为状态轨线上的点数。建立预测模型如下

(10)

问题即转化为求解多元回归函数问题。

2 结果分析

利用1961—2016年共672个月哈尔滨市月气温序列进行前期试验，包括参数敏感性试验、SFA信号分析等，对2017—2020 年48个月气温作独立样本预测。

2.1 对参数进行敏感性试验

通常计算嵌入维数的方法是以嵌入定理为依据的，而气候时间序列为非平稳系统，该方法不再适用，因此需要依靠经验和试验来分析SFA慢特征信号对参数选取的敏感性，最终确定适合研究的参数。选取哈尔滨市气温序列为实际非平稳时间序列对m进行敏感性试验，设置时滞参数τ=1，变化m的取值范围，分别提取气温序列的慢特征信号。图3给出了部分试验结果，由图可见，当m取值为5、9、13时，提取的慢特征信号的变化趋势和月际间变化都比较接近，只是在峰值和谷值附近存在微小差异。随m值的增大，慢特征信号的振幅减小，曲线噪音减小，平滑度逐渐增大。可见，在一定范围内选取m值，提取出的慢特征信号差别不大。参考前人研究并结合敏感性试验结果，本文对气温序列提取慢特征信号时设定嵌入维数m=11，时滞参数τ=1。

图3 不同嵌入维数m=5(a)、m=9 (b)、m=13(c)、m=22 (d)、m=31(e)提取的哈尔滨市月气温慢特征信号比较

2.2 哈尔滨市气温的慢特征信号

依据敏感性试验结果将参数设置为m=11，τ=1。利用SFA方法提取1961年1月至2016年12月哈尔滨市月平均气温距平序列的慢特征信号(图4)。由图4可见，慢特征分析方法提取的SFA信号更加平滑，但能较好地反映原序列的时间变化趋势、高低转换、极值等信息，进一步计算可知，提取的慢特征信号变率[22]对气温序列变率的贡献率为57%。二者相关系数R=0.6，通过了99.9%信度的显著性检验。

图4 1961—2016年哈尔滨市月气温距平序列(a)及提取的SFA信号(b)变化

2.3 哈尔滨市气温SFA信号的时间尺度特征

对提取的哈尔滨市气温SFA信号进行Morlet小波变换，由图5中SFA信号的小波功率谱可以看到，哈尔滨气温SFA信号具有4 a和7 a左右两个较显著的年际尺度周期振荡，且2.0—7.8 a的周期均通过95%置信度的显著性检验。与以往研究得到ENSO事件的2—7 a[23]年际尺度周期类似。相关分析表明，哈尔滨市气温SFA信号与前期3—12个月的NINO3.4区海温指数显著正相关，相关系数通过了95%信度检验。侯依玲等[24]研究也得到中国东北地区年平均气温一致型的时间系数存在显著的2—7 a周期，指出中国东北北部地区气温受ENSO等大尺度气候背景影响显著。因此，哈尔滨气温的变化可能与前期赤道东太平洋海温变化相关，但相应的物理机制还需进一步探讨。

图5 1961—2016年哈尔滨市气温序列SFA信号的小波全局功率谱

2.4 哈尔滨市气温的预测试验

在提取了哈尔滨市气温慢特征信息的基础上，构建包含慢特征信号的预测模型，并分析拟合和预测结果。在评价SFA信号预测能力的基础上滚动预测近4 a哈尔滨市逐月气温距平。

试验使用1961—2016年共672个月气温数据来进行建模及预测试验，使用相同长度的150个子数据序列的平均预测结果来评价预测方程，主要评价指标为方程拟合及预测的相关系数和均方根误差(RMSE)。

每个子序列前面40 a的数据用于提取SFA信号并建立预测函数，预测时间步长为1—12个月。时滞参数τ取为1，{xt}为气温距平序列，嵌入维数m1取为3—8，{αt}为慢特征信号，嵌入维数m2取为0—3。m2=0代表预测方程中不包含慢特征信号，即平稳性模式。m2=1—3代表预测方程中嵌入1—3个维数的慢特征信号，简称慢特征模式。

由图6a可以看到，m2=0平稳性模式拟合的相关系数在预测时间步长为1—2，即超前1—2个月预测时，通过了95%置信度的检验。时间步长大于2时，相关系数保持在0.2左右，没有通过95%置信度检验。当m2=1—3，即加入了慢特征信号后，前1—5步拟合相关系数明显增大，且随嵌入维数m2增大相关系数略增大。除了m2=1在第4—5步时相关系数值在0.4—0.6之间外，其余情况第1—5步的相关系数值都超过了0.6。而从第6步开始，即预测超前6个月以上时，拟合相关系数急剧下降，接近95%置信度临界线。在全部时间步长里，慢特征模式的相关系数都高于平稳性模式，步长为1—5时，慢特征模式相关系数偏高明显。由图6b可见，预测的相关系数m2=0时在全部时间步长均未通过95%置信度检验。m2=1—3时曲线形态在预测时间步长为1—5步时和拟合曲线接近，相关系数都通过95%信度检验，但值略低于拟合结果，第6步开始相关系数值急剧下降至0值附近，明显低于图6a的0.25，即第6步以后可预报性较小。在图6a和图6b中，相关系数最大值均出现在预测时间步长为第5步时。

图6 气温预测模型拟合的(a)、预测的(b)相关系数和拟合的(c)和预测的(d)均方根误差

拟合的均方根误差(图6c)在m2=0时明显偏大，误差值在1.7—1.9之间变化，预测步长为1时，误差最小，第2—3步明显上升，之后稳定维持。m2=1—3时，即加入慢特征信号后，在预测步长为1—5步时，均方根误差明显偏小，误差值在1.4—1.5之间变化，第5步时误差有明显下降，之后误差明显增加，第7步以后接近常值，但略小于m2=0的误差。随嵌入维数m2增加，均方根误差略有减小。预测的均方根误差(图6d)形态与拟合的均方根误差相似，但误差值整体均略大于拟合的误差值。拟合和预报结果均在时间步长为第5步时，均方根误差最小。

试验结果表明，引入慢特征信号后建立的哈尔滨市月气温预测模型在预测时间步长为1—5，即提前1—5个月预测时，相关系数明显高于平稳性模型，预测误差也明显小于平稳性模型。这表明在一定的预测时间步长内，引入慢特征信号的预测模型可以提高预测能力和精度。嵌入维数m2=3，预测时间步长为5时，预测效果最优。

2.5 哈尔滨市月气温预测

依据2.4试验方案，对哈尔滨市2017年1月至2020年12月共48个月气温进行滚动预测。设定相空间嵌入维数m1=8，m2=3，时间步长k=5。逐月气温预测及与实况对比结果见图7。预测结果统计表明，平稳性模型m2=0的预测同号率为0.40左右(19/48)，预测平均均方根误差为1.7 ℃，而慢特征模式m2=3预测同号率为0.71(34/48)，预测平均均方根误差为1.5 ℃。可见，引入慢特征信号的预测模型效果优于平稳性模型。

图7 气温独立样本预测与实况的比较

3 结论与讨论

(1)慢特征分析方法可以从Logistic映射时间序列中提取出与原始外强迫信号拟合较好的慢特征信号，其慢变和快变分量与原始外强迫信号仅有位移和振幅差别。

(2)SFA方法可以有效地提取哈尔滨市气温序列中的慢特征信号。提取的SFA信号能够反映原气温序列曲线的变化趋势、极值等信息。

(3)拟合和预测试验表明，引入SFA信号后的哈尔滨市气温预测模型可以在一定程度上提高预测能力和精度。48个月独立样本滚动预测试验也表明引入慢特征信号后预测效果优于平稳性模型。

(4)慢特征分析方法中参数的选择，是通过试验尝试并参考以往文献主观选取的，缺乏客观性判断指标，如何更加合理地选取嵌入维数等参数还需要进一步研究。利用SFA方法提取慢特征信号只是一种数学算法，并不能解释提取的慢特征信号所代表的物理含义。功率谱分析能够得到慢特征信号的显著周期尺度，但其所代表的外部影响因子，也需要相应的物理机制来佐证。黑龙江省地处中高纬，气温变化的成因非常复杂，除受外强迫因子影响外，大气环流因子的影响也很重要。提取的慢特征信号与环流因子之间的作用关系，二者对气温变率的贡献等还需要结合更多的诊断分析方法来探讨。