基于多模式集成冬半年气温预报偏差修正

齐铎 刘松涛 赵广娜 高梦竹

(黑龙江省气象台，黑龙江 哈尔滨 150030)

引言

随着经济和社会的发展，人们对天气要素预报的精细化、准确化程度的需求不断提高。基于统计方法，利用偏差订正技术对模式预报进行释用，是当前获取高时空分辨率要素预报的众多方法中效率较高、成本较低的一种。

对于模式气温预报的偏差订正主要基于两种思想,即对单一模式的偏差订正和对多模式的集合。早期的订正方法多基于单一模式或产品进行释用。吴启树等[1]利用MOS思想建立预报量与订正量之间的一元线性回归方程，对ECMWF的模式气温预报进行订正。李佰平和智协飞[2]利用一元线性回归、多元线性回归、单时效消除偏差和多时效消除偏差平均的订正方法，对ECMWF模式地面气温预报结果进行订正，结果表明4种方法都能有效改进地面气温预报。李莉等[3]利用卡尔曼滤波递减平均方法对T213模式的高空温度及地面气温预报偏差进行订正，结果表明该方法对系统误差有很好的订正能力。马旭林等[4]在卡尔曼滤波递减平均的一阶矩和二阶矩偏差订正方案的基础上发展了综合偏差订正方案，对日本气象厅区域集合预报模式(JMA)的850 hPa温度预报进行订正，结果表明综合偏差订正方案能有效改善集合预报偏差和离散度偏小的问题。王婧等[5]利用平均法、双权重平均法、滑动平均法和滑动双权重平均法等四种订正方法对GRAPES_RAFS的2 m温度预报进行订正，结果表明滑动双权重平均法效果最优。双权重方法与卡尔曼滤波递减平均法原理相似，都是考虑训练期内不同偏差的贡献不同，卡尔曼滤波递减平均假设时间越接近，预报偏差特征越相似，而双权重方法更多通过权重来减少离群资料对预报偏差统计的影响[5-6]。薛谌彬等[7]在动态滑动双权重订正方法的基础上进一步考虑了温度订正预报空间连续性的问题，采用空间偏差逐步订正法，提高空间连续性，结果表明空间逐步订正可以进一步改善地形造成的温度订正能力的差异。卡尔曼滤波递减平均订正和双权重订正方法都能很好地改善模式预报，对模式系统误差有很好的订正能力，但是在某些地区、某些时段，对模式直接输出预报存在负订正的现象[7-8]。

近年来研究发现模式本身不仅有系统误差，还有初值的不确定性，使数值模式不可避免地存在预报偏差。数值预报的发展方向由确定性预报转向集合预报。基于集合思想的多模式集成预报在温度预报订正中开始广泛应用。研究表明[9-13]，集成预报可显著优于任何参与集成的单一成员的预报，从而修正单一模式偏差订正中出现的负订正现象。

选择预报效果好的模式进行集成预报，才能获取更好的预报结果[14]。因此，选择当前所有可以获取的气温格点预报中效果最好的EC、EC_COR[8]及SCMOC，对以上3种气温预报结果进行集成。另外，训练期的选取对于订正效果而言非常重要，对于不同的温度预报要素和不同季节及不同地理位置，最优训练期的选择有很大差异[1,7,10,14]。滑动训练期是指根据模式的变化动态调整偏差订正量，从而获得更好的预报效果[10]。因此，利用消除偏差集合平均(以下简称BREM)方法，选择动态最佳滑动训练期进行集成预报，希望以此来消除卡尔曼滤波对EC带来的负订正效果，并进一步提高温度客观预报质量。

1 资料与方法

1.1 资料来源

选取检验和订正范围为40.90°—56.00°N，118.65°—137.55°E中国境内区域的格点(黑龙江省智能网格预报责任范围，下同)。检验和订正时段选择2019年10月1日至2020年4月30日冬半年时间，而训练资料时间为2019年1月1日至9月31日。

SCMOC地面气温预报及日最高、最低气温预报，空间分辨率为0.05°×0.05°，时效为0—240 h，时间分辨率为逐3 h。本文以20时起报(北京时，下同)为例。

EC气温预报空间分辨率为0.125°×0.125°，利用双线性插值法插值到与SCMOC一致的网格上。时间分辨率：0—72 h预报时效为逐3 h，72—240 h为逐6 h，内插为逐3 h时效的预报。EC预报资料获取时间滞后，17时以前仅能获取08时起报资料，为了业务需要，选择12—240 h预报时效的资料(相当于SCMOC预报时效中0—228 h)来进行订正和融合。因此，EC及EC_COR预报及相关的检验结果缺少231—240 h预报时效的时段，在相关图表中以缺测处理。

气温实况(GOBS)采用全国智能网格实况融合分析产品(V2.0)中CLDAS实时气温数据产品[15]，空间分辨率为0.05°×0.05°。目前，该资料在数值模式检验评估的相关研究和预报业务中广泛应用[16-17]。

1.2 检验与订正方法

1.2.1 检验方法

温度预报准确率(Fa)

(1)

考虑到实际预报业务，认为误差小于2 ℃的预报即为准确预报，因此温度预报准确率定义为温度预报绝对误差不大于2 ℃的样本在所有预报样本中所占的百分比。因此，式(1)中，Fa是温度预报绝对误差不大于2 ℃的百分率；Nr为预报气温与实况气温之差不超过±2 ℃的总格点(次)数；NF为预报的总格点(次)数。

平均绝对误差(TMAE)和平均误差(TME)

(2)

(3)

式(2)—式(3)中，Tfc(i)、Tob(i)分别为预报和GOBS值；n为需要时空平均的样本数量；i为第i个样本。

相对订正量(又称温度预报技巧评分，Tss)

Tss=(TMAEN-TMAEF)/TMAEN×100%

(4)

式(4)中，TMAEN为订正前的平均绝对误差；TMAEF为订正后的平均绝对误差。

另外，用BREM_EC代表BREM对EC的相对订正量；类似的BREM_EC_COR和BREM_SCMOC分别代表BREM对EC_COR和SCMOC的相对订正量；EC_COR_EC代表EC_COR对EC的相对订正量。

1.2.2 订正方法

除了对EC进行卡尔曼递减平均订正[8]外，用消除偏差集合平均方法(简称BREM)对多种预报结果进行集成。求训练期内的各模式平均误差，用各模式预报值减掉各自训练期内平均误差，得到多模式消除偏差的集合平均。

消除偏差集合平均方法[11]

(5)

动态最优滑动训练期选取：对2019年1月1日至9月31日3—72 h逐3 h、逐格点的5—70 d、间隔5 d的滑动训练期得到的集成预报的平均绝对误差进行比较，发现一半以上的最小平均绝对误差对应的滑动训练期日数集中在5—15日。因此，在集成预报前，计算前10 d对应的5—15日、间隔1日的滑动训练期的集成结果的平均绝对误差。根据最小平均绝对误差动态确定最优滑动训练期。

1.2.3 多预报集成技术路线流程图

多预报集成技术路线如图1所示。由于针对格点进行订正，所以对订正后的格点预报(包括EC_COR和BREM)的空间分布及时间演变特征与GOBS进行对比，发现其空间及时间的连续性与GOBS基本一致(图略)。

图1 多预报集成技术路线流程图

2 结果分析

2.1 内插法时间降尺度的合理性评估

为了解EC预报在60—228 h时效(集成预报20时起报的预报时效，实际08时起报的EC预报时效为72—240 h)、6 h预报间隔，经过内插法降尺度为3 h的预报结果对预报准确率及模式偏差订正的影响，在EC模式未经过降尺度处理的时段内，选择3—24 h预报时效(图2a、图2c和图2e)，在降尺度处理时段内随机选取75—96 h预报时效(图2b、图2d和图2f)进行对比分析。从准确率上看，75—96 h时效的变化特征，与3—24 h时效的变化特征完全一致。对基于EC预报的EC_COR和BREM预报结果，是否经过内插处理对于误差的统计结果区别不大。

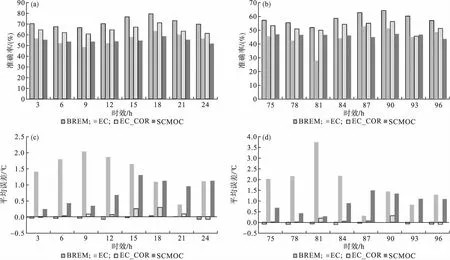
图2 3—24 h时效(a)和75—96 h时效(b)逐3 h的2 m气温预报2 ℃准确率，3—24 h时效(c)和75—96 h时效(d)逐3 h的2 m气温预报2 ℃平均误差，3—24 h时效(e)和75—96 h时效(f)逐3 h的2 m气温预报2 ℃平均绝对误差

2.2 预报结果随时效变化特点

为了解不同预报结果的总体特征和随时效变化的特点，对3—240 h内逐3 h地面气温及日最高、最低气温的≤2 ℃预报准确率(简称准确率)、平均误差及平均绝对误差进行统计分析。

逐3 h预报误差变化具有显著的日变化特点(图2)，且日变化特征对于不同预报时效而言是相对一致的(图略)。根据图2可知逐3 h对于不同的预报，其结果均表现为夜间预报准确率低，白天预报准确率高的特点(图2a和图2b)。预报准确率最低的时间一般出现在每日05时(北京时，对应以20点起报的9 h、33 h、57 h、……、225 h预报)，准确率最高出现在14时前后。参与集成的三种预报中，EC_COR准确率最高，EC和SCMOC准确率基本相当，仅在69 h(图略)和93 h预报时效SCMOC准确率略高。BREM方法的集成结果较参与集成的预报而言，准确率都有明显的提升。平均误差可代表模式偏差的统计特征[10]，不同的预报结果偏差的特点略有不同(图2c和图2d)，EC预报总体上表现为系统性偏高的特点，夜间偏高幅度较大，白天反之；EC_COR平均误差显著减小，一般仍以系统性偏高为主，11—14时平均误差相对较大，但都在0.4 ℃以下，说明卡尔曼滤波方法可显著消除模式的系统误差；SCMOC的偏差也表现为系统性偏高，但日变化特点与EC显著不同，白天平均误差相对较大，偏差与EC量级相当，夜间平均误差较小，与平均绝对误差日变化特征相反，使白天的平均误差与平均绝对误差更接近，表现为以系统性误差为主，而夜间则相反，表现为随机误差为主；BREM的系统性误差在不同的预报时段内都很小，预报结果一般表现为以气温预报偏低为主，夜间偏低幅度相对更大。说明BREM在卡尔曼滤波的基础上，消除预报的系统误差幅度偏大。随着预报时效的延长，不同预报结果的准确率都表现为显著下降的特点，下降幅度最高可达50%以上(图略)；96 h以后，预报的平均绝对误差显著增大，其中预报效果最好的BREM的平均绝对误差都超过2 ℃(图2e和图2f)。

最高、最低气温的特点与逐3 h地面气温特点一致，随时效延长，预报准确率下降(图3a和图3b)。经过集成以后，BREM的预报效果明显优于其他任何一种预报。值得注意的是，对于三种参与BREM的预报，96 h及其以前的最高气温预报，准确率最高为SCMOC。除EC_COR外，其他三种预报结果在大多时段表现为最高气温预报准确率略高于最低气温的特点。最高气温预报的平均误差对于不同预报也有所不同(图3c和图3d)，EC最高、最低气温的平均误差都很大，一般在2.0—2.5 ℃；SCMOC次之，最低气温预报偏高幅度较小，为0.5 ℃左右，最高气温预报偏高幅度在0.5 ℃以上；EC_COR也以偏高为主，其中最低气温预报偏高幅度较小一般在0.2 ℃以内，最高气温预报偏高幅度在0.3—0.5 ℃；BREM平均误差数值很小，且平均预报结果较实况偏低为主，偏低幅度一般都低于0.1 ℃，最高温度预报的平均误差几乎为0 ℃。平均绝对误差随预报时效延长显著增加(图3e和图3f)，预报效果最好的BREM平均绝对误差小于2 ℃的预报时效，对于最低气温而言在72 h预报时效以内，对于最高气温而言在96 h以内。平均误差随预报时效增幅远远小于平均绝对误差，从某种程度上可以说明，随预报时效的延长各种预报结果都表现为随机误差增大的特点。

图3 24—240 h时效日最低气温(a)和日最高气温(b)预报2 ℃准确率，24—240 h时效日最低气温(c)和日最高气温(d)预报平均误差，24—240 h时效日最低气温(e)和日最高气温(f)预报平均绝对误差

2.3 不同时效预报误差的月际变化

平均误差(简称ME)反映模式预报的系统误差，而平均绝对误差(简称MAE)同时包含着系统误差和随机误差的统计特征。虽然在不同时效上所有预报都表现为预报较实况一致的系统性偏高或是系统性误差不明显，且随预报时效延长MAE增加的特点(图2c和图2d；图3c和图3d)。但不同月份之间表现有显著差异，气温偏低的月份更倾向于表现出预报较实况一致系统性偏高的特点(图4)；不同预报都表现为气温低的月份、夜间气温(图5)MAE更高，预报误差更大。针对不同的预报结果，具体的误差特征又有所不同，BREM(图4a)偏差较小、ME的绝对值一般在1 ℃以内，其中50%以上ME绝对值小于0.4 ℃，4月白天预报偏低，夜间特别是02时前后及最低气温(图略)预报较实况偏高，10月相反，其他月份较实况一致偏低；BREM(图5a)在1月的MAE相比其他月份更大，MAE一致小于2 ℃的预报时效仅在30 h以内，其他月份可延长至78 h。EC_COR(图4c)偏差幅度相比BREM有所提高，ME绝对值小于1 ℃的约占50%，其他主要集中在1—2 ℃，2—4月预报较实况偏低，11月至翌年1月预报较实况偏高，10月也以偏高为主，仅14时前后及最高气温(图略)预报较实况偏低；EC_COR(图5c)MAE表现较BREM次之，11月至翌年3月所有时效均大于2 ℃，10月、4月MAE相对较小，30 h时效内一般小于2 ℃。EC(图4b)更多表现为预报较实况偏高，且偏高幅度一般都在2 ℃以上，其中夜间及最低气温(图略)偏高的幅度更大，10月、4月白天或14时前后存在预报较实况偏低2 ℃以上的特点；EC(图5b)的MAE最大值出现在12月和11月，几乎都在2 ℃以上，其他月份的表现与EC_COR接近。SCMOC(图4d)预报也以较实况偏高为主，白天偏高幅度在1—2 ℃，其中4月有所不同，白天偏低，夜间偏高；SCMOC(图5d)几乎在所有月份、所有时效MAE都在2 ℃以上。

图4 BREM(a)、EC(b)、EC_COR(c)和SCMOC(d)3—240 h时效逐3 h平均误差逐月分布

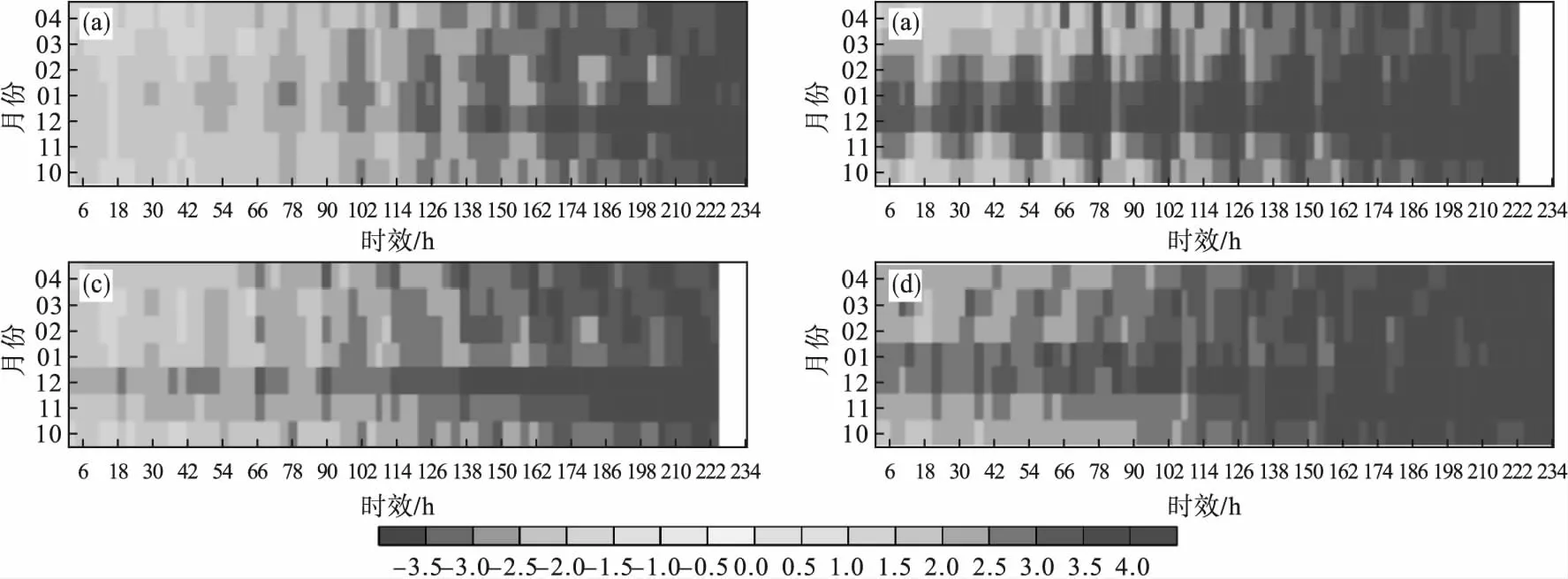
图5 BREM(a)、EC(b)、EC_COR(c)和SCMOC(d) 3—240 h时效逐3 h平均绝对误差逐月分布

2.4 集成预报修正能力评估

从4种预报结果随预报时效变化特点上看，在分析的区域和时段内，BREM结果均好于EC、EC_COR及SCMOC等任意一种单一预报的效果。前期对于卡尔曼滤波订正(EC_COR)效果的评估结果表明[8]，总体上EC_COR对EC气温预报有显著的订正能力，但是在EC预报能力相对较高的月份和地区存在负订正的现象。即订正后的预报误差反而高于订正前模式直接输出的预报误差。为了解BREM在不同月份的表现，以及对不同月份中EC_COR对EC偏差负订正的修正能力，下面给出了地面气温(图6)预报中BREM分别对EC、EC_COR及SCMOC的相对订正量随月份和预报时效的变化，并且与EC_COR对EC的相对订正效果进行对比。另外，由于最高气温与白天的气温、最低气温与夜间气温的变化特点基本一致，所以仅分析逐3 h气温相对订正量随时效和季节的变化。

BREM相对订正量分布特点表现为，随预报时效的增加相对订正量减小，夜间相对订正量多高于白天(图6a、图6c和图6e)。其中，对SCMOC(图6e和图6f)的相对订正效果更好，相对订正量一般在10%以上，在189 h时效以后出现少量的无法通过显著性检验的负订正。对EC(图6a和图6b)的相对订正量较SCMOC偏低，但也多在10%以上，显著正订正比例在70 %以上，虽然负订正的比例增加，但是无法通过显著性检验，相比EC_COR(图6g和图6h)对于EC的10 %以上的显著负订正，对EC的订正效果有明显提升。对EC_COR(图6c和图6d)的订正能力最低，显著正订正占比约为40%，显著负订正的时次占比不及5%，显著负订正主要集中在1月的42—156 h范围内的部分预报时效，2月也有少量分布，这个时段内EC_COR订正能力比较高，特别在1月，EC_COR对EC的相对订正量几乎都大于30%，在EC_COR对EC显著负订正时次出现较多的11月、3月和4月，BREM对EC_COR表现为显著的正订正。与EC_COR对EC的相对订正量分布基本相反，说明在EC_COR对于EC订正效果好、EC_COR预报准确率高的时候，BREM对于EC_COR的订正能力有限。但其中仍有例外，对于12月EC_COR对EC有很好的订正效果，但是BREM在此基础上又对EC_COR预报效果进一步提升。

图a、图c、图e、图g中单位为%；图b、图d、图f、图h中不同色标代表不同的显著性水平

总体而言，BREM可显著修正EC_COR对于EC偏差负订正的问题，但是在EC_COR对EC偏差订正效果好的基础上再进一步提高预报准确率的能力有限。

3 结论与讨论

(1)内插方法对温度进行插值，与不用插值的平均绝对误差及2 ℃准确率日变化趋势基本一致，对于平均误差在插值时段内，还表现出一定程度的误差偏小的特点。总体而言，利用内插的方式进行时间降尺度，在时间降尺度幅度不大的情况下是一种简便有效的预报生成手段。

(2)随预报时效的延长，BREM、EC、EC_COR及SCMOC等四种预报准确率都表现为显著下降的特点，BREM的准确率下降幅度最大；四种预报都表现为白天气温(日最高气温)预报准确率高(平均绝对误差小)、夜间气温(日最低气温)预报准确率低(平均绝对误差大)；EC整体呈现系统性偏高的特点，偏高幅度白天小、夜间大；SCMOC预报也表现为系统性偏高的特点，但系统误差总体小于EC，白天系统性偏高幅度更大，与平均绝对误差变化正好相反，夜间随机误差更高；EC_COR仅在白天有正的系统误差，随机误差与SCMOC相同也是夜间高于白天；BREM的平均误差在0—240 h时效内都很小。

(3)BREM、EC、EC_COR及SCMOC等四种预报，平均绝对误差在11月至翌年2月相比其他月份偏高；不同时效都表现为系统性一致偏高或者系统性偏差不明显，但是偏差特征在不同月份表现不一致：气温偏低的月份更倾向于表现出预报较实况一致偏高的特点。集成预报系统误差小，平均误差的绝对值一般在1 ℃以内；EC_COR系统误差相比集成大，2—4月系统性偏低，11月至翌年1月系统性偏高，10月也以偏高为主，其中14时前后预报较实况偏低；EC在10月、4月的白天或14时前后存在预报较实况偏低的特点；SCMOC在4月有所不同，白天预报较实况系统性偏低。

(4)总体上看，BREM能有效地修正EC_COR对EC负订正的现象。在EC_COR订正能力比较高的情况下，BREM与EC_COR的订正效果相当甚至更优。即可在EC_COR基础上进一步提升预报质量。另外，利用BREM方法对高质量预报产品的融合(不局限于模式直接输出预报或是订正预报)可获取较单一预报更优的预报结果。

(5)本文仅利用模式直接输出和基于模式直接输出的各类订正预报产品，研究集成和融合方法对各类预报产品的订正效果，方法较为简单，并未考虑预报误差的地区性差异，下一步打算根据模式误差的地域差异设计改进多模式集成方案，获取针对不同误差特征的多模式集成预报。模式的统计释用方法，主要针对模式的系统误差进行订正，而对于模式的随机误差订正无能为力。但系统误差根据不同的统计方式又有不同的特点，所以选择不同的训练期，得到的系统误差不同，对于模式的订正能力就有很大影响。有研究表明，模式对于不同的天气背景，偏差特征有所不同[18]，针对不同的天气形势，对系统误差进行统计，从而进行订正，也许是在基于最优滑动训练期方法进行偏差订正以后，预报偏差订正能力得以进一步提升的一种可行途径。