模和环的JGP-内射性

鲁 琦，鲍宏伟，赵玉梅

(蚌埠学院 数理学院，安徽 蚌埠 233030)

本文中的环R均是含单位元的结合环，R上的模是酉模.J(J(R))，Zl(Z(RR))和Zr(Z(RR))分别表示R的Jacobson 根、左和右奇异理想.对R中的元a，l(a)(r(a))表示a的左(右)零化子.内射性的研究是近年来环论的热门研究课题之一[1-4]，同态也是群论及环论中的重要研究内容[5-7].Yousif 等在文献[1]中引入JP-内射环和JGP-内射环的概念，证明了它们是GP-内射环的真推广，将Chen 在文献[2]中关于GP-内射环的若干重要结果推广到JGP-内射环，证明了对右Kasch 右JGP-内射环，R/J是半单的当且仅当R是左有限维的.Zhu 在文献[3]中定义了JGP-内射模，对其进行了等价刻画，研究其和半本原环的关系，又在文献[4]中借助JGP-内射环研究了某些特殊环的关系，并用JGP-内射环刻画了QF-环，丰富了关于QF-环的某些结论.

本文利用左JP-内射环刻画左自内射环，并借助模和环的JGP-内射性研究环的半本原性.文中研究了单奇异左R-模是JGP-内射的环的半本原性和非奇异性，并用文献[8]中左GWZI 环替换文献[9]中拟ZI-环，证明了若环R是左GWZI 环，且任意单奇异左R-模是GP-内射的，则R是左、右非奇异的.本文中的一些结果推广了文献[2]和[10]的相关结果.

设R是环，L是R的左(右) 理想，若对任意0 ≠a∈L，存在正整数n，满足an≠0，且anR⊆L(Ran⊆L)，则称L是R的W-理想[11].设L是R的左(右)理想，若对任意a∈L，存在正整数n，使得anR⊆L(Ran⊆L)，则称L是R的GW-理想[12].由文献[11]例1.2 可知GW-理想是W-理想的真推广.称环R是左GWZI 环[8]，若对任意a∈R，l(a)是R的GW-理想.本文中出现的其它概念和术语可参见文献[13].

1 JGP(JP)-内射模(环)

称环R是左JP-内射环[1]，如果对任意a∈J(R)，均有rRlR(a)=aR.环R称为左JGP-内射环[1]，如果对任意0 ≠a∈J(R)，存在正整数n，满足an≠0，且rRlR(an)=anR.类似可定义右的情形.特别地，若J(R)=0，则R是左、右JGP-内射环.称左R-模M是JGP-内射的[3]，如果对任意0 ≠a∈J(R)，存在正整数n，使得an≠0，且Ran到M的任意左R-同态可延拓为R到M的左R-同态.

命题1设M是左R-模，则下列条件等价：

(1)M是JGP-内射的；

(2) 对任意0 ≠a∈J(R)，存在正整数n，满足an≠0，且rMlR(an)=anM；

(3) 对任意0 ≠a∈J(R)，存在正整数n，使an≠0，且对Ran到M的任意左R-同态f，存在m∈M，满足f(ran)=ranm,r∈R.

证明(1)和(2)的等价见文献[3]定理8 .

(2) ⇒(3) 设M是JGP-内射的，f是Ran到M的任意左R-同态，则对任意x∈lR(an)，可得xan=0，且f(xan)=x f(an)=0.故

于是存在m∈M，使f(an)=anm.

(3) ⇒(2) 对任意y∈rMlR(an)，下证y∈anM.对任意r∈R，定义容易验证f是左R-同态，故由条件可知，存在m′∈M，使得f(ran)=ranm′.所以y=f(an)=anm′∈anM，再由y的任意性可得rMlR(an)⊆anM.注意到anM⊆rMlR(an)是显然的，因此rMlR(an)=anM，M是JGP-内射的.证毕.

推论1环R是左JGP-内射环当且仅当对任意0 ≠a∈J(R)，存在正整数n，使an≠0，且对Ran到R的任意左R-同态f，存在b∈R，满足f(ran)=ranb,r∈R.

称环R是约化的[14]，如果R不含非零幂零元.称R是ZI-环[15]，如果a,b∈R，由ab=0可推出aRb=0.易知，约化环是ZI-环.

命题2若R是约化的左JGP-内射环，S=eRe,e2=e∈R，则S是约化的左JGP-内射环.

证明因为R约化，所以S约化.∀0 ≠a∈J(S)，易知a∈J(R).由R是左JGP-内射环，可知存在正整数n，使an≠0，且rRlR(an)=anR.下证rS lS(an)⊆anS.∀x∈rS lS(an)，则有lS(an)⊆lS(x).∀y∈lR(an)，可得yan=0，进而推出eyean=0，故eye∈lS(an)⊆lS(x).由此可得eyex=0.注意到(yx)2=yxyx=yx(eyex)=0，再由R是约化的，可得yx=0，故y∈lR(x)，所以lR(an)⊆lR(x).因此rRlR(x)⊆rRlR(an)=anR.因为x∈rRlR(x)，所以存在c∈R，使x=anc.而x∈S，故x=xe=ance=anece∈anS，因此rS lS(an)⊆anS.易见anS⊆rS lS(an)，故可得rS lS(an)=anS，命题2 得证.证毕.

推论2JGP-内射模的直和项仍是JGP-内射模.

定理1设R是环，则下列条件等价：

(1)R是半本原的；

(2) 任意a∈R，Ra是 JGP-内射的；

(3)R的本质左理想均是JGP-内射的.

证明(1) ⇒(3) 显然.

(3) ⇒(2) 对任意a∈R，存在左理想K，使Ra⊕K是R的本质左理想.由(3)及推论2 得Ra是JGP-内射的，故(2)得证.

(2) ⇒(1) 由文献[3]定理12 可得.证毕.

定理2若环R的任意极大本质左理想是JGP-内射的，且R的左零化子是W-理想，则R是半本原环.

证明对任意0 ≠a∈J(R)，下证若a2=0，则r(a)是R的理想.对任意t∈r(a)，得at=0，所以a∈l(t).因为l(t)是W-理想，所以aR⊆l(t).故aRt=0，进而可得Rt⊆r(a)，因此r(a)是R的理想.于是存在R的左理想I，使r(a)⊕I是R的本质左理想.由于r(a)是理想，且a∈r(a)，可得aI⊆r(a)∩I=0，故I⊆r(a)，因此r(a)是R的本质左理想.从而存在极大本质左理想M，使得r(a)⊆M.由定理2 条件，M是左JGP-内射的，且注意到a2=0，故左R-同态r∈R可延拓为R到M的左R-同态.因此存在m∈M，使得a=am.所以1-m∈r(a)⊆M，进而推出1=(1-m)+m∈M，矛盾.因此J(R)是约化的.

对0 ≠a∈J(R)，存在R的左理想K，使Ra⊕K是R的本质左理想.若Ra⊕K=R，则存在e=e2∈R，使得Ra=Re，故e∈J(R)，矛盾.因此Ra⊕K≠R，于是存在极大本质左理想M，使得Ra⊕K⊆M.因为J(R)是约化的，所以a2≠0，再由定理2 条件，M是左JGP-内射的，可知存在正整数n，使a2n≠0.由J(R)是约化的，可知J(R)是ZI-的，故若ra2n=0，则(ra)2n=0，因此ra=0.容易验证r∈R是左R-同态，于是存在m∈M，使得a=a2nm，进而推出a(1-a2n-1m)=0.注意到a∈J(R)，故1-a2n-1m可逆，从而得a=0，矛盾.因此J(R)=0.证毕.

下面定理3 和定理4 分别推广了文献[2]中定理2.8 和定理3.9.

定理3若R是左Kasch，左JGP-内射的半局部环，则R是有限上生成的右R-模.

证明因为R是半局部环，所以有，Mi是极大左理想.对任意1≤k≤n，不妨令因此由文献[2]引理2.7 可得由文献[1]定理3.8（1）可知r(Mi)是极小右理想，故r(J)是有限生成右理想.再由文献[1]定理3.8(3)，(4)可知Soc(RR)=r(J)，且Soc(RR)=Soc(RR)是R的本质右理想.故由文献[13]命题10.7 得R是有限上生成的右R-模.证毕.

定理4若R是左JGP-内射环，且R/Soc(RR)（或R/Soc(RR)）满足左零化子ACC 条件，则J是幂零的.

证明记S=Soc(RR)，=R/Soc(RR).对J中的任意元a1,a2,a3,···，由满足ACC 条件，可知存在正整数m，使得

对任意正整数n，由文献[1]定理3.6 可知a1a2···anan+1∈J⊆Zl，故l(a1a2···anan+1)是R的本质左理想，从而S⊆l(a1a2···anan+1).注意到S⊆l(an+1)，由文献[2，定理3.9]的证明，可得

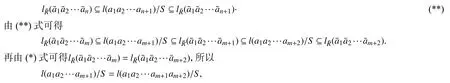
故可得l(a1a2···am+1)=l(a1a2···am+1am+2)，从而R(a1a2···am+1)∩l(am+2)=0.因为am+2∈J⊆Zl，所以l(am+2)是本质左理想.故a1a2···am+1=0，由此证得J是左T-幂零的，所以(J+S)/S是R¯的左T-幂零理想.由文献[13]命题29.1，可知(J+S)/S是幂零的.于是存在正整数t，满足Jt⊆S.故Jt+1⊆JS=0，因此J是幂零的.

若R/Soc(RR)满足左零化子ACC 条件，对任意a∈J，由于Soc(RR)⊆l(J)⊆l(a)，故类似前面的证明，可得J是幂零的.证毕.

引理1[16]若M/N是半单的，N是M的真子模，则对任意M的子模L，存在M的子模K，使得L+K=M，且L∩K⊆N.

定理5设R是半局部环，则R是左自内射环当且仅当R是左JP-内射环.

证明左自内射环显然是左JP-内射环.设f是R的左理想K到R的左R-同态.由R是半局部的以及引理1 可得存在左理想L，使得K+L=R，且K∩L⊆J.对任意x∈K∩L，由于R是左JP-内射环，故Rx到R的任意左R-同态可延拓为R的自同态.因此存在R的自同态g，使得g(x)=f(x).对任意r∈R，存在k∈K,l∈L，使得r=k+l.在R上定义映射F，F(r)=f(k)+g(l).如果k1+l1=k2+l2，ki∈K,li∈L,i=1,2，则k1-k2=l2-l1∈K∩L，故f(k1-k2)=g(l2-l1).因此F(k1+l1)=F(k2+l2).容易验证F是左R-同态且F|K=f，所以R是左自内射环.证毕.

推论3若R是半局部的左JP-内射环，且满足左零化子ACC 条件，则：

(1)R是半完全环；

(2)R是QF-环.

证明(1) 由定理5 可得R是左自内射环，所以J=Zl.因为左零化子ACC 条件，所以Zl=J是诣零的，从而由文献[13]命题27.1 可得R/J的幂等元可提升.因此R是半完全环.

(2) 由文献[17]引理5.3.1 中的(1)，(4)的等价可得.证毕.

2 单奇异左R-模是JGP(GP)-内射的

易见半本原环是左(右)JGP-内射环，但反之不真(见文献[1]例3.1).若R是半本原环，则任意单奇异左R-模是JGP-内射的.由文献[18]例1.1 可知，存在环R，使任意单奇异左R-模是JGP-内射的，但R不是半本原的.

命题4若任意单奇异左R-模是JGP-内射的，则J是约化的当且仅当R是半本原的.

证明若R是半本原的，则显然J是约化的.假设J是约化的.对任意0 ≠a∈J，先证Ra∩l(a)=0.对任意x∈Ra∩l(a)，可知存在r∈R，使得x=ra，且xa=ra2=0.由J是约化的，可得l(a)=l(a2)，故x=0，由此证得Ra∩l(a)=0.

令L=Ra⊕l(a)，若L=R，则存在b∈Ra,c∈l(a)，使得1=ba+c.于是可得a=ba2+ca=ba2，进而推出(1-ba)a=0.由a∈J可得a=0，矛盾.所以L≠R.于是存在左理想K，使得L⊕K是R的本质左理想.若L⊕K≠R，则存在极大左理想M，使得L⊕K⊆M，从而R/M是单奇异左R-模.故存在正整数n，使得an≠0，且由J是约化的，可得l(a)=l(an).对任意r∈R，容易验证f:Ran→R/M;ranr+M是左R-同态，于是存在c∈R，使得1+M=f(an)=anc+M，故可得1-anc∈M.注意到a∈J⊆M，所以1∈M，矛盾，因此L⊕K=R.于是存在e2=e∈R，使得Ra=Re.而0 ≠a∈J，故矛盾.因此R是半本原的.证毕.

定理6若任意单奇异左R-模是JGP-内射的，且Zl⊆J，则R是左非奇异环.

证明若Zl≠0，则存在0 ≠a∈Zl，a2=0，且l(a)是R的本质左理想.由于l(a)≠R，故存在极大本质左理想M，使得l(a)⊆M，且R/M是单奇异左R-模.对任意r∈R，容易验证f:Ra→R/M;rar+M是左R-同态.于是存在b∈R，使1-ab∈M，再由a∈J可得1∈M，矛盾.故Zl=0，R是左非奇异环.证毕.

推论4设R是左AGP-内射环，若任意单奇异左R-模是JGP-内射的，则：

(1)R是左非奇异环；

(2)R是半本原环.

证明由R是左AGP-内射环及文献[19]推论2.3 可知J=Zl.若Zl≠0，则存在0 ≠a∈Zl，a2=0.由定理6 的证明可得Zl=0，R是左非奇异环.再由J=Zl可得R是半本原环.证毕.

定理7设任意单奇异左R-模是JGP-内射的，若R的任意补左理想是GW-理想，则R是半本原环.

证明由命题4，只需证J约化.设存在0 ≠a∈J，a2=0.若Ra+l(a)≠R，则存在极大左理想M，使得Ra+l(a)⊆M.可以证明M是R的本质左理想.若不然，则M是R的直和项，于是存在0 ≠e2=e∈R，使得M=l(e)，进而可得a∈l(e).由定理7 条件，Re作为补左理想是GW-理想，可知存在正整数n，使en≠0，且enR(=eR)⊆Re，于是可得eR(1-e)⊆Re(1-e)=0，从而ea=eae.由于R(1-e)是R的补左理想，类似前面的证明，可得ae=eae，因此ae=ea.因为a∈l(e)，所以ea=0，从而可得e∈l(a)⊆l(e).因此，e2=0，矛盾.故M是R的极大本质左理想，从而R/M是单奇异左R-模.对任意r∈R，容易验证f:Ra→R/M;rar+M是左R-同态.故存在b∈R，使得1-ab∈M.因为a∈J⊆M，所以1∈M，矛盾，故可得Ra+l(a)=R.于是存在c∈Ra，使得a=ca，故(1-c)a=0.因为c∈Ra⊆J，所以a=0，矛盾.因此J是约化的.证毕.

定理8设任意单奇异左R-模是JGP-内射的，若R的任意补右理想是GW-理想，则R是半本原环.

证明只需证J约化.设存在0 ≠a∈J，a2=0.若Ra+l(a)≠R，则存在极大左理想M，使得Ra+l(a)⊆M.由定理8 条件，eR作为补右理想是GW-理想，故存在正整数n，使en≠0，且Ren(=Re)⊆eR.于是可得(1-e)Re⊆(1-e)eR=0，从而ae=eae.由于(1-e)R是R的补右理想，同理可得ea=eae，因此ae=ea.再由定理7 的证明可得，J是约化的，故定理8 得证.证毕.

称R是左GWZI 环[8]，若对任意a∈R，l(a)是GW-理想.称R是π-半交换环[20]，若对R的任意元a和b，如果ab=0，则存在正整数n，使得anRbn=0.左GWZI 环必为π-半交换环，但反之不真[20].称R是拟ZI-环[9]，若对R的任意非零元a，b，如果ab=0，则存在正整数n，使得an≠0，且anRbn=0.易见，拟ZI-环是π-半交换环，下例说明π-半交换环未必是拟ZI-环.

例1设R′=Q〈α,β,γ〉是系数取自有理数域的以α,β,γ为非交换未定元的多项式的集合.I是由〈α2,β2,γ2,αγ,βα,γβ,γα〉生成的理想.记R=R′/I，则容易验证R是π-半交换环.注意到所以R不是拟ZI-环.容易验证R也是左GWZI 环.

引理2[8]若R是左GWZI 环，则R的幂等元是中心的.

下面命题5 部分推广了文献[10]引理1.1.

命题5若R是左GWZI 环，且任意单奇异左R-模是GP-内射的，则R是约化的.

证 明设存在0 ≠a∈R，a2=0，则l(a)≠R.于是存在左理想L，使l(a)⊕K是R的本质左理想.若l(a)⊕K=R，则存在e2=e∈R，使l(a)=Re，且由引理2 可知a=ae=ea.因为a∈rl(a)=(1-e)R，所以a=ea=0，矛盾.故l(a)⊕K≠R.于是存在极大本质左理想M，使得l(a)⊕K⊆M，从而R/M是单奇异左R-模.由命题5条件，容易定义左R-同态f:Ra→R/M;rar+M，r∈R.于是存在b∈R，使1-ab∈M.进而可得b-bab∈M，且由ba2=0可得ba∈l(a)⊆M.由于R是左GWZI 环，故可知l(a)是R的GW-理想，于是存在正整数n，使得(ba)nb∈l(a)⊆M.从而可得

于是(ba)n-1b=(ba)nb+(ba)n-1(b-bab)∈M.继续下去，可得bab∈M.于是b=（b-bab）+bab∈M，所以ab∈M.故可得1∈M，矛盾.因此对任意0 ≠a∈R，均有a2≠0，从而可得R是约化的.证毕.

推论5若R是左GWZI 环，且任意单奇异左R-模是JGP-内射的，则R是半本原环.

证明设存在0 ≠a∈J，a2=0，则l(a)≠R.由命题5 的证明可知，存在极大本质左理想M及b∈R，使1-ab∈M.由a∈J可得ab∈J，故1∈M，矛盾.因此J是约化的.再由命题4 可得R是半本原环.证毕.

由命题5 和文献[9]引理3.3 可得下面的定理9.

定理9设R是左GWZI 环，且任意单奇异左R-模是GP-内射的，则R是左、右非奇异的.

推论6[10]设R是半交换的左YJ-内射环，且R是左GP-V′-环，则R是右非奇异的.

定理10若环R是π-半交换环，且任意单奇异左R-模是JGP-内射的，则R是半本原的.

证明由命题4，只需证J是约化的.设存在0 ≠a∈J，a2=0，则l(a)≠R.于是存在左理想K，使l(a)⊕K是R的本质左理想.若l(a)⊕K≠R，则存在极大本质左理想M，满足l(a)⊕K⊆M，从而单奇异左R-模R/M是JGP-内射的.容易定义左R-同态f:Ra→R/M;rar+M，r∈R.于是存在b∈R，使1-ab∈M.注意到a∈J，故可得1∈M，矛盾.故l(a)⊕K=R.于是存在e2=e∈R，使l(a)=Re，再由a∈l(a)可得a∈Re.由文献 [20，命题2.7]可知a=ae=ea，注意到a∈rl(a)=(1-e)R，所以a=ea=0，矛盾.故可得J是约化的.因此R是半本原的.证毕.

推论7若环R是π-半交换的右AGP-内射环，且任意单奇异左R-模是JGP-内射的，则R是右非奇异环.

证明由定理10 及文献[19]推论2.3 可得证.证毕.

定理11设R是π-半交换的左GP-内射环，且任意单奇异左R-模是GP-内射的，则R是左、右非奇异环.

证明由文献[21，定理2]可得J=Zl，再由定理10 可得R是左非奇异的.类似文献[10]定理2.1 的证明，可得R是右非奇异的，故定理得证.证毕.