基于Matlab的蚁群算法求解旅行商问题

河南科技职业大学 严玉芳

蚁群算法是一种解决组合优化问题的算法，具有灵活性、稳健性等优势，而旅行商问题正是一个利用蚁群算法得以解决的经典选择优化问题。本文首先以蚁群算法为研究对象，阐述了蚁群算法的基本原理、模型的建立以及算法的实现流程，其次讨论了蚁群算法在经典的旅行商问题上的应用，最后利用Matlab软件对旅行商问题进行编程求解并对最终实验结果进行了分析。

群体智能优化算法来自于对自然界中的有生物种在寻觅食物时所做出的行为的仿真模拟。这种算法是将搜索和优化的所有过程模拟为生物个体进化或者觅物的过程，将搜索范围中的点看作是自然界中的生物个体，把求解问题的各个目标函数度量为生物个体对自然环境的适应能力，最后将生物个体的适者生存的淘汰过程或者生物个体觅食的过程当作搜索和优化的过程中的较好可行解。群体智能算法也被人们称为群集算法，比较常见的有：蚁群算法（ACO）、粒子群算法(PSO)、遗传算法(GA)、菌群算法(BF)等，其中蚁群算法采用的是一种正反馈机制，具有高于一般传统算法的发现较优解的能力。

1 蚁群算法原理

通过研究蚁群觅食的行为过程，学者们发现蚂蚁能在没接收到任何有关食物源的线索或提示下，靠本能寻找到一条最优路径（即蚁穴到食物源所在地点间的最短距离）的主要原因在于蚂蚁之间的信息传递主要是依靠它们在所经过路径上分泌出的一种具有挥发性的名为“信息素”的物质[1-3]。即蚂蚁个体在前进时，若遇到前一个蚂蚁分泌出的这种物质，便能根据信息素的强度有选择的寻找路径，并且与其他蚂蚁选择到同一路径的概率与信息素的量以及浓度成正比。正是受蚂蚁寻觅食物所做出的行为的启发，学者们才提出了蚁群算法。

2 蚁群算法

2.1 模型建立

想象蚁群内任一只蚂蚁都是简单的、智能的个体，已知蚂蚁选择节点是依靠某种概率进行的，并且它是每两个节点之间的距离以及在连接这两个节点路径上的信息素的量的函数，蚂蚁将会在行走的路径上分泌适量的信息激素且蚂蚁不会二次经过已走过的节点。蚂蚁在t时刻选择t+1时刻要到达的节点，在此时间间隔内，对m只蚂蚁调用迭代算法一次，每只蚂蚁完成对所有城市的一遍旅行且一次旅行进行n次迭代算法。当蚂蚁k完成一次完整闭合路径且计算其长度Lk后，得有关信息强度公式：且

其中i,j(i,j= 1,2,3...,n)表示节点，bi(t)表在t时刻时节点i内的蚂蚁数目；τij(t)表t时刻(i,j)上的信息素强度；ρ(0 ≤ρ≤1)表信息素挥发后的剩余度[1]；Q为常数；1 -ρ表在时间t到t+n内的信息素挥发；为路径(i,j)的能见度，为蚁群(t,t+n)时间内在路径(i,j)上留下的单位长度的路径的信息素数量。

利用禁忌表tabuk(s)禁止蚂蚁对已访问过的节点重复访问，得到从节点i到j的转移概率：

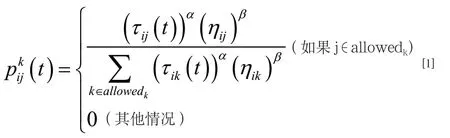
其中allowedk= {N-tabuk}，α和β是控制路径及能见度的重要参数。如果(i,j)之间的距离短，则ηij较大ρij较大，即距离近的节点被选择的概率大于距离远的节点被选择的概率[2]。

2.2 算法实现

蚁群算法的实现可由以下流程图简单展示，如图1所示：

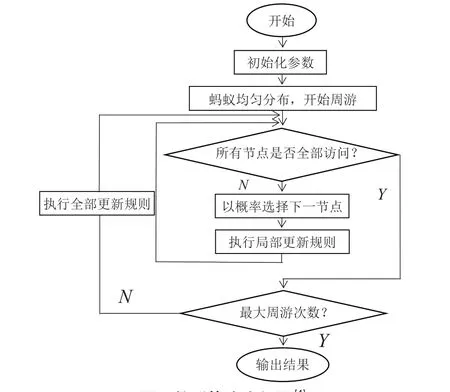
图1 蚁群算法流程图[4]Fig.1 Ant colony algorithm flowchart

3 蚁群算法的应用—基于蚁群算法求解旅行商问题

3.1 旅行商问题（Traveling Salesman Problem）

旅行商问题（Traveling Salesman Problem，简称TSP）是最为基本的选择最优路径的问题[5]。此问题具体来说就是一个推销商想要到n个城市推销产品，在已知各城市间的距离的前提下，希望找出最短回路，即选择一条最短的路径且这条路径能使得商人从起点出发并将每个城市都正好走过一遍之后又回到原点处。

3.2 旅行商问题（TSP）的数学规划模型

假设ijd为每两个城市i与j之间的距离，即弧长(i,j)的长度为。归结在图论意义下，则其图论可描述为：给定图G，记为赋权图G= (V,E)，其中V为顶点集，表示n个城市的集合，E为边集，表示连接两城市的路的集合，各顶点间的距离是ijd。引入决策变量，则旅行商问题的目标函数为：，约束条件为

在上述数学规划模型中，约束条件1和2表明对于任意的点，只有一条边进入另一条边出去；约束条件3确保了不会有回路解得产生。故约束条件1、2和3共同保证了所求得的解可构成满足题目条件的回路。

3.3 利用蚁群算法求解旅行商问题的基本思路

利用蚁群算法在求解组合优化类问题上的先进性，可以将蚂蚁看作是旅行商，将各个节点看作旅行商要访问的城市，将蚂蚁放置在不同的城市上，利用多次迭代的方式不断对数据进行优化，最后求出蚂蚁完成周游所行走的最短路线以及距离。

3.4 利用蚁群算法求解旅行商问题的基本步骤

由蚁群算法的实现流程图，再结合实际的旅行商问题，可以总结出解决旅行商问题的基本步骤，如表1所示：

表1 基于蚁群算法求解旅行商问题Tab.1 To solve TSP based on ant colony algorithm

4 有关算法实现的部分程序展示

初始状态程序：x=[41 37 54 25 7 2 68 71 54 83 64 18 22 83 91 25 24 58 71 74 87 18 13 82 62 58 45 41 44 4]；

求解程序：function [R_best，L_best，L_ave， Shortest_Route，Shortest_Length]=ACATSP(C，NC_max，m，Alpha，Beta，Rho，Q)；

5 生成数据以及部分图形显示

利用Matlab[7]对问题进行编程生成数据的过程中由于有参数的存在，且参数对数据的影响不可忽略，故对参数α，β，ρ在α=1.5，β=2，ρ=0.1，Q=106的基础上，对参数组进行不断的改变，NC_max=100为最大迭代次数，且每个数据计算五次并记录下最优解以及平均解。在本次求解中，规定TSP城市个数为30，并且将运行得出的具体结果以及路径选择图形（仅展示部分图形）展示如下：

（1）参数组α=1，β=2，ρ=0.1，Q=106下的路径选择，如图2所示：

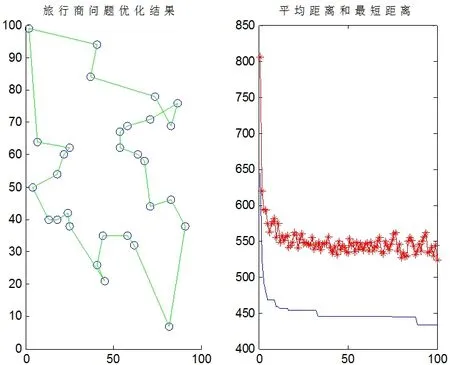
图2 路径选择Fig.2 Path finding

（2）不同参数组下的最终计算结果，如表2所示：

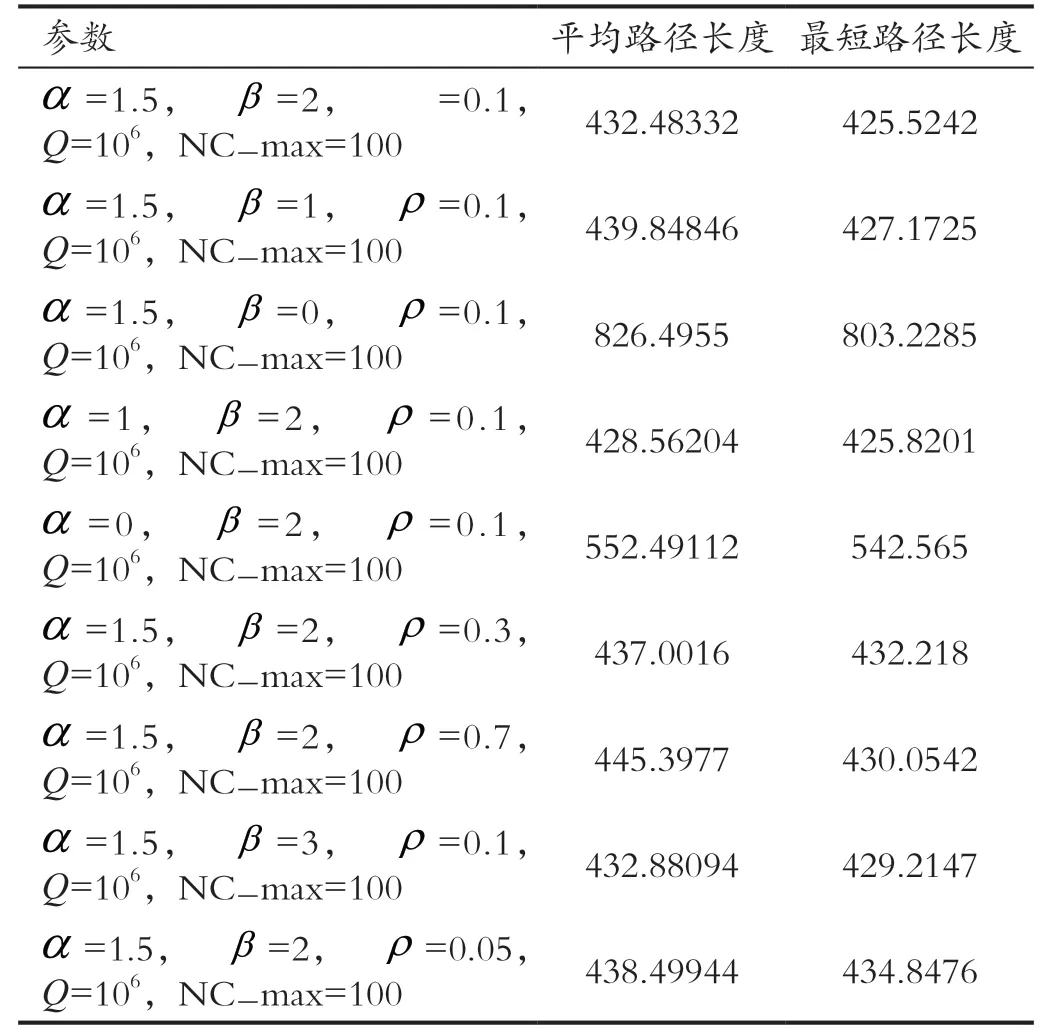
表2 基于蚁群算法求解旅行商问题的计算结果Tab.2 The calculation results of solving TSP based on ant colony algorithm

（3）数据结果分析

从上面的表格数据可以看出，对于城市数据为30的旅行商问题可以做出以下几种讨论：

在参数α=1.5，ρ=0.1，Q=106，NC-max=100一直稳定的情况下，对β=2，β=1，β=0，β=3四个不同β数据下的平均路径以及最短路径长度进行对照可以得出：当β=2时，最大最小迭代以及平均迭代次数均为100，其最小路径长度为425.5242，平均路径长度为432.48332，是四个β数据选择中路径值达到最小的一个。

在参数β=2，ρ=0.1，Q=106，NC-max=100一直稳定的情况下，对α=1.5，α=1，α=0三个不同α数据下的平均路径以及最短路径长度进行比照可以得出：当α=1时，最大最小迭代以及平均迭代次数均为100，其最小路径长度为425.8201，平均路径长度为428.56204，是三个α数据选择中路径值达到最小的一个。

在参数α=1.5，β=2，Q=106，NC-max=100一直稳定的情况下，对ρ=0.1，ρ=0.3，ρ=0.7，ρ=0.05四个不同ρ数据下的平均路径及最短路径长度进行比照可得：当ρ=1时，最大最小迭代及平均迭代次数均为100，其最小路径长度为425.5242，平均路径长度为432.48332，是四个ρ数据选择中路径值达到最小的一个。

总结上面的分析可得在α＞1时路径长度递增，α＜1时路径长度减小；同理ρ＞0.1时路径长度逐渐增加，ρ＜0.1路径长度逐渐减小，β＜2时路径长度也在减小，β＞2时路径长度增加，经过比较可以得出在这个算例中，最优参数的选择应该是α=1，β=2，ρ=0.1。

6 结语

本文主要是向读者介绍蚁群算法运用到现实生活问题中并对问题进行解决的具体事例，利用蚁群算法来对问题进行求解将会把问题的复杂程度逐渐降低。众所周知旅行商问题是一种经典的复杂组合求最优解的问题，本章就是以经典问题作为算例，以蚁群算法为基础，利用Matlab软件对其进行编程求解，最后对求解结果进行分析并得出最终结论。