The pseudoscalar meson and baryon octet interaction with strangeness S = -2 in the unitary coupled-channel approximation

Bao-Xi Sun and Xin-Yu Liu

Faculty of Science, Beijing University of Technology, Beijing 100124, China

Abstract The interaction of the pseudoscalar meson and the baryon octet with strangenessS= -2 and isospin I =1 /2is investigated by solving the Bethe–Salpeter equation in the infinite and finite volume respectively.It is found that there is a resonance state generated dynamically, which owns a mass of about 1550 MeV and a large decay width of 120–200 MeV.This resonance state couples strongly to the πΞ channel.Therefore, it might not correspond to the Ξ( 1620)particle announced by Belle collaboration.At the same time,this problem is studied in the finite volume,and an energy level at 1570 MeV is obtained, which is between the πΞ and resholds and independent of the cubic box size.

Keywords: Bethe–Salpeter equation, chiral unitary approach, amplitude

1.Introduction

respectively.Moreover, there is also some evidence of the Ξ( 1690)particle with the same data sample [2].

The masses of these two particles are about 300 MeV higher than that of the Ξ hyperon, and thus they can be regarded as excited states of the Ξ hyperon.However, they are difficult to be described within the framework of the constituent quark model.

The unitary coupled-channel approximation of Bethe–Salpeter equation in the finite volume has made a great success in the study of the meson–meson interaction [7–12] and the meson–baryon interaction[13,14].Actually,a scheme to simulate the Lattice data in order to obtain the kernel of Bethe–Salpeter equation in the unitary coupled-channel approximation is proposed in these articles.Sequently an attempt has been made to fit the lattice finite volume energy levels fromπηscattering and the properties ofa0(9 80) is evaluated [15].This method is also extended to study the interaction of theπD,ηDandchannels inJP=0+in the finite volume by fitting the lattice QCD calculation results[16],and along with this clue,more research works have been done by various groups worldwide.

In this work, the interaction between the pseudoscalar meson and baryon octet with strangenessS= -2 will be studied, and then the Bethe–Salpeter equation in the infinite and finite volume will be solved within the unitary coupledchannel approximation respectively.We will try to distinguish whether there are resonance states generated dynamically or not, and if so, whether the resonance state can be treated as a counterpart of the Ξ(1620)particle.

This article is organized as follows.In section 2, the potential of the pseudoscalar meson and baryon octet is constructed.In section 3,a basic formula on how to solve the Bethe–Salpeter equation in the unitary coupled-channel approximation is shown.Consequently, the pole position in the complex energy plane is obtained by solving the Bethe–Salpeter equation in the infinite volume, and its coupling constants to different channels are calculated.The chiral unitary approach in a finite box is introduced in section 4 .Finally, the summary is given in section 5.

2.Interaction of the pseudoscalar meson and the baryon octet

The Weinberg–Tomozawa contact term of the pseudoscalar meson and the baryon octet takes the form of

whereis the total energy of the system,MiandMjdenote the initial and final baryon masses,EandE′ stand for the initial and final baryon energies in the center of mass frame,respectively.The coefficientCijfor the sector of strangenessS= -2 and charge zero is listed in table 1, Moreover, we assume the decay constants are only relevant to the pseudoscalar meson withfη=1.3fπ,fK= 1.22fπandfπ=92.4MeV, as given in [17–21].

Table 1.The coefficientsCij in the pseudoscalar meson and baryon octet interaction with strangenessS= -2 and chargeQ =0,Cj i= Ci j.

In the interaction of pseudoscalar meson and baryon octet, the contact potential originated from Weinberg–Tomozawa term plays a dominant role, and the correction from the s- and u-channel potentials can be neglected [21].The Weinberg–Tomozawa term of the pseudoscalar meson and the baryon octet is only related to the Mandelstam variables, therefore, it only gives a contribution to the S-wave amplitude in the scattering process of the pseudoscalar meson and the baryon octet.

respectively.Thus the coefficientsCijin the Weinberg–Tomozawa contact potential of the pseudoscalar meson and the baryon octet can be obtained in the isospin space, which are summarized in table 2.

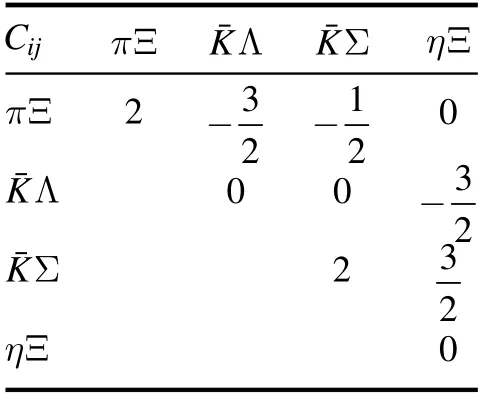
Table 2.The coefficientsCij in the pseudoscalar meson and baryon octet interaction with strangenessS= - 2and isospin I =1 /2,Cj i= Ci j.

In the case of isospinI=3 /2and strangenessS= -2,the interaction of the pseudoscalar meson and the baryon octet is repulsive, therefore, no resonance states can be generated dynamically.

3.Bethe–Salpeter equation

The potentialV(p,k;q,P-q)in equation (7) can be divided into an on-shell part and an off-shell part.At the meson–baryon threshold, the on-shell part of the potential is dominant and the off-shell part can be absorbed into the on-shell part of the potential if a suitable renormalization of coupling coefficients is performed.After that,the on-shell part of the potential can be taken out from the integral in equation (7) and the Bethe–Salpeter equation becomes an algebra equation when the onshell approximation is taken into account, i.e.

with the meson–baryon loop function

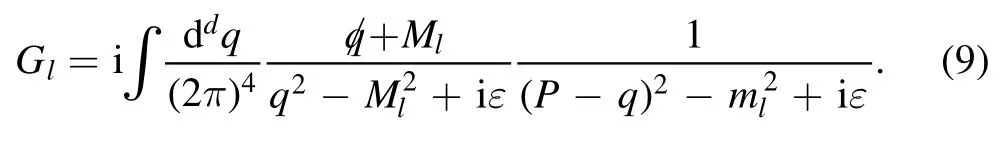
The analytical form of the loop functionGin equation (9)can be obtained in the dimensional regularization scheme.In[22], supposing+Ml= 2Ml,a simplifeid form of the loop function in the dimensional regularization scheme is written as

wherestands for the three-momentum of the meson or the baryon in the center of mass frame, andμdenotes the regularization scale andal(μ) represents the subtraction constant.Although the regularization scale and the subtraction constant should be canceled by the higher-order contact terms in the perturbative theory, they are treated as fitting parameters in the unitary coupled-channel approximation.Apparently, these parameters reflect the influence of higher order terms not included in the potential when the Bethe–Salpeter equation is solved, just as iterated in [18, 19].

Actually, the on-shell condition+Ml= 2Mlis valid only when it acts on the real baryon.When the loop functionGin equation (9) is calculated, the analytical form can be obtained directly without the on-shell condition taken into account, just as done in [20]:

Table 3.The subtraction constants aij used in the calculation, where the regularization scale takes the value of 630 MeV, i.e.μ = 630MeV.

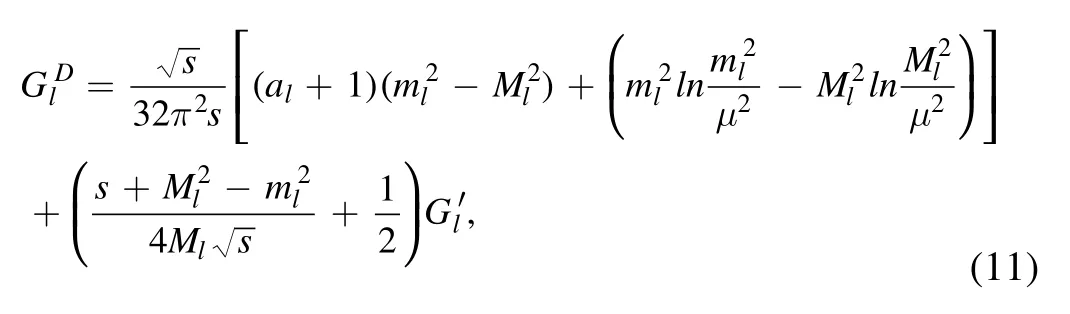
where some off-shell corrections have been taken into account.Although the on-shell condition*q* +Ml=2Mlis eliminated when the loop function is evaluated in the dimensional regularization scheme, the form of the Bethe–Salpeter equation in equation (8) should be solved in the present work, but not the formula in equation (7).Therefore,the whole calculation is carried out in an on-shell approximation.

In this work, these two kinds of loop functions will be adopted in the calculation,and the results will be compared to each other.As done in [20, 21], a transition of

is made when the Bethe–Salpeter equation is solved.Therefore, the scattering amplitude

becomes dimensionless.

The subtraction constants in the loop function of equations (10) and (11) are listed in table 3, which are cited from[3].The regularization scaleμis set to equal to the cutoff momentum of 630 MeV in order to obtain the same results as in [23], where theK¯Ninteraction is investigated with a loop function in a momentum cut-off scheme by solving the Bethe–Salpeter equation.However, recently in the study of heavy mesons consisting ofcorbquarks, the regularization scale is usually fixed to 1 GeV, just as done in [24].Moreover, the relation of the regularization scale in the dimensional regularization scheme to the maximum momentum in the momentum cut-off scheme is discussed in detail in theBK¯andBsπinteraction [25].

With these subtraction constants and the regularization scaleμ=630MeV, the amplitudes of pseudoscalar meson and baryon octet are evaluated by solving the Bethe–Salpeter equation in the unitary coupled-channel approximation.A pole is detected around 1550 MeV in the complex energy plane and the pole position and coupling constants obtained with the loop functions in equations (10) and (11) are summarized in tables 4 and 5, respectively.Since the real part ofthe pole position is higher than the πΞ threshold, and lower than theΛ threshold, it lies in the second Riemann sheet and can be regarded as a resonance state with strangeness S= -2 and isospin I =1 /2.When the values of these subtraction constants change,the mass of this resonance state changes slightly, while the decay width of it changes in the range of 120–200 MeV.Apparently, both the mass and the decay width of this resonance state are far away from the experimental value supplied by Belle collaboration, and the results are also different from those in [3].

The coupling constants are calculated according to

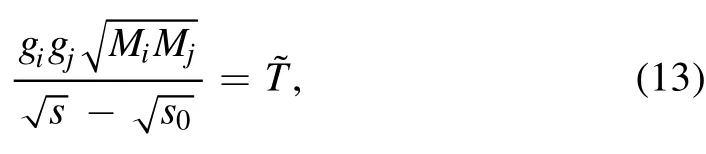
Table 4.The pole position and corresponding coupling constants gi for different parameter sets calculated with the loop function in equation (10), where the pole position in the complex energy plane is in units of MeV.

From tables 4 and 5, it is found that the real part of the pole position is about 100 MeV higher than the πΞ threshold and 50 MeV lower than thethreshold, hence it would mainly be a πΞ resonance state and couples strongly to the πΞ channel.However, the Ξ ( 1620)particle announced by Belle collaboration almost locates at thethreshold in the range of uncertainty, hence it is more possible to be a molecule state ofand should couple strongly to thechannel.Therefore,the resonance state generated dynamically in the unitary coupled-channel approximation would not correspond to the Ξ ( 1620)particle reported by Belle collaboration.In [3], in order to obtain a resonance mass close to the Ξ(1620)’s,the pion decay constant fπis enlarged, and an averaged value of f = 1.123fπis adopted,just as done in their another work to discuss the antikaon-nucleon interaction[23].In [3], the resonance state still couples strongly to the πΞ channel except for the result with Parameter set 5.In Parameter set 5,the subtraction constants of πΞ andchannels take values of -3.1and -1.0respectively, which deviate from -2 largely.Although there are no constraints on the range of the subtraction constant, a value around -2 is adopted usually when the Bethe–Salpeter equation is solved,as in[22],where the antikaon-nucleon scattering is discussed in the unitary coupled-channel approximation.Fortunately,by comparing the loop function in the dimensional regularization scheme with that of the momentum cut-off form at the threshold, a mass dependent formula of the subtraction constant for a fixed regularization scale is established in the study of the pseudoscalar meson and heavy meson interaction[24].It is no doubt that this relation supplies a hint on how to determine the subtraction constant values when the Bethe–Salpeter equation is solved,and we will adopt it in the future work of this region.Apparently, theS= -2 resonance state generated dynamically in the unitary coupled-channel approximation is different from the Ξ ( 1620)particle announced by Belle collaboration.In order to discover this resonance state, the decay process of→Ξ-π+π+should be analyzed carefully,especially in the S-wave part.As far as the large decay width is concerned, it might be difficult to find it.

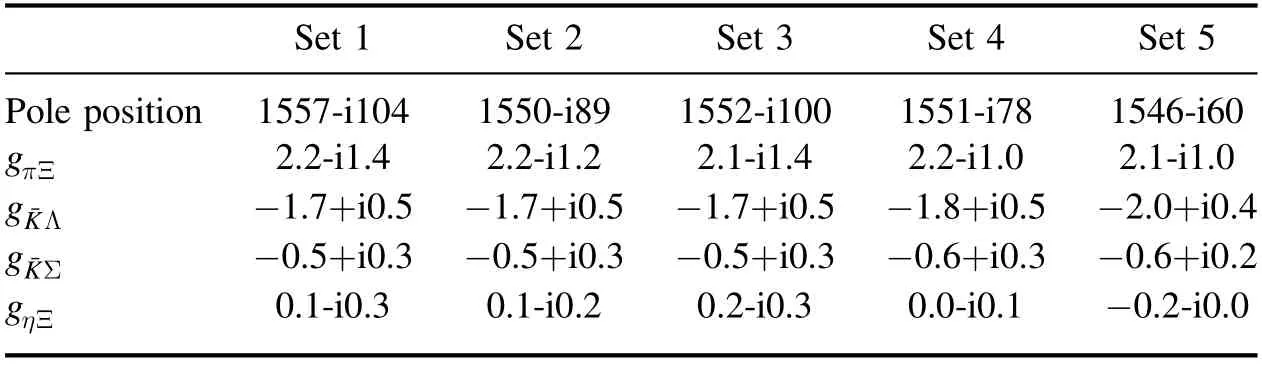
Table 5.The pole position and corresponding coupling constants gi for different parameter sets calculated with the loop function in equation (11), where the pole position in the complex energy plane is in units of MeV.

4.The chiral unitary approach in a finite box

In order to obtain the energy level in a finite box, the loop function in equation(11)should be replaced by awhen the Bethe–Salpeter equation is solved, where

Figure 1.Real part of the last two terms of the right hand side of equation (14) for the channel.The solid line indicates the case with the analytical form in equation (17), while the dashed line represents oscillation results calculated with equation (14) directly.

where

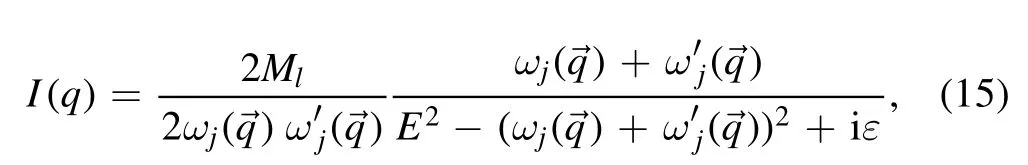
and

withLthe cubic box side,

In a finite box, the discrete momenta of particles are summed as done in equation(14).At this point,it is different from the case in the infinite volume,where the momentum is continuously changed.The sum in equation (14) can be simplified when the multiplicities of the same→ are considered.In figure 1, the real part of-GDfor thechannel is shown, which oscillates withqmaxincreasing.However, it converges whenqmax→+∞.

An analytical form on the integral in equation(14)can be found in the erratum of [26].For the meson–baryon interaction, the integral in equation (14) is written as

The energy levels obtained in the box for different values ofLare depicted in figure 2,and a smooth behavior of energy levels as a function ofLis observed.In figure 2, the first 3 energy levels are almost invariant when the cubic box sizeLincreases.Especially, the lowest and third levels are close to theπΞ andthresholds, respectively, therefore, they do not correspond to bound states of the pseudoscalar meson and baryon octet, but indicate the threshold effect in the finite volume.The second level lies at 1570 MeV, which is higher than theπΞ threshold, and can be regarded as a resonance state with strangenessS= -2 and isospinI=1 /2.Apparently, this energy level is far away from the mass of the Ξ( 1620)particle announced by Belle collaboration, and it would not be a counterpart of the Ξ ( 1620)particle.At this point, it is consistent with the conclusion obtained in the infinite volume in section 3.

Figure 2.Energy levels as functions of the cubic box size L,derived from the chiral unitary approach in a box and using (E ) in equation (14).

5.Summar y

In this work, the interaction of the pseudoscalar meson and the baryon octet with strangenessS= -2 and isospinI=1 /2 is investigated by solving the Bethe–Salpeter equation in the unitary coupled-channel approximation.It is found that a resonance state is generated dynamically around 1550 MeV, which owns a decay width of about 120–200 MeV.Thus this resonance state is not consistent with the Ξ ( 1620)particle announced by Belle collaboration.The coupling constants of this resonance state to different channels are calculated, and it couples strongly to theπΞ channel.Furthermore,this problem is also studied by solving the Bethe–Salpeter equation in the finite volume, and the energy levels at different cubic box sizes are obtained.It is found that the second energy level in the vicinity of 1570 MeV might be a resonance state of the pseudoscalar meson and baryon octet, while the first and third levels may come from theπΞ andthresholds, respectively.

ORCID iDs