A new effective potential for deuteron

Taha Koohrokhiand Sehban Kartal

1 Department of Physics, Faculty of Sciences, Golestan University, Gorga n, Iran

2 Istanbul University, Department of Physics, 34000, Istanbul, Turkey

Abstract We calculate for the first time the static properties of the deuteron, within the framework of supersymmetric quantum mechanics, analytically.A new effective potential and its partner are derived from a superpotential so that all parameters are fitted by the experimental data.An analytical expression is obtained for the deuteron wave function and contributions of the orthogonal 13S1 and 13D1 states are determined,explicitly.Compared to one pion exchange,the superpotential produces an electrostatic as well as two pion exchange terms for the potential.The saddle point radius of the potential and the maximum of the wave function are linearly proportional.In comparison with other methods, the approach presented in this paper is a new and extensible symmetry-based approach that, despite its straightforward calculations and explicit analytical expressions, provides a good explanation for two-body effective interactions such as two-nucleon systems and diatomic molecules.

Keywords: superpotential, Boson exchange, supersymmetry, effective potential

1.Introduction

The deuteron is the simplest nucleus consisting of two nucleons.The study of deuterons provides useful information about static nucleon–nucleon(NN)interactions.The one pion exchange potential(OPEP)is an extended version of Yukawa potential that dominates in nucleon spacings above 3 fm,and is reasonable for spacings above 2 fm.However, theoretical and experimental studies have shown that the nuclear force is not just a matter of an exchange of single pion [1].In addition, the exact study of NN interactions requires a more fundamental theory.Nevertheless, with good approximation,at long ranges, nucleons can still be considered structureless particles and OPEP suitable for describing the NN interaction.

In general, NN interactions have been studied based on several main groups: quantum chromo dynamics (QCD)[2–4], lattice QCD [5–7], effective field theory (EFT) [8],Chiral EFT[9–11],chiral perturbation theory[12–14],boson exchange (BE) models [15–17], mean field theory [18–20]and phenomenological NN potentials[21–23].In most of the models, potentials have quite complicated structures and are described by many parameters.Indeed an efficient theory is a theory that, while having simple calculations and reproduction of expected values, has good insights, predictions and straightforward to be developed.

Supersymmetry(SUSY)was originally conceived within the quantum field theory as a means to unify the mathematical treatment of bosons and fermions [24–26].In this regard,supersymmetric quantum mechanics (SUSY QM) is a development of quantum mechanics that introduces new concepts such as superpotential, partner potentials, Hamiltonians hierarchy, and shape invariant potentials.The mathematical strategies in SUSY QM not only solve many problems algebraically but also classify potentials into different categories and determine criteria for them.Furthermore, approximation methods in SUSY QM provide more accurate results than those in conventional quantum mechanics [24].The theoretical successes of SUSY have caused its applications rapidly to be extended into other branches of physics and mathematics, i.e.supersymmetric quantum chromodynamics [27] as well as nuclear physics[28], by the unification of fermionic and bosonic fields to a superfield.

This paper is the first study of static properties of deuteron by SUSY QM.Given the excellent results achieved,this approach can be developed straightforwardly to considerdetails of the interaction.Despite the simplicity of the calculations presented in this study, the proposed superpotential not only describes the long ranges of the interaction well but also gives notable results for intermediate and short ranges.The new attitude presented in this paper has introduced a new effective potential for deuteron that is also applicable for twobody interactions such as diatomic molecules.

Table 1.Static properties of deuteron.

2.Potential and superpotential

2.1.OPEP

The OPEP is the potential derived from meson theory in the treatment of the NN system [29], and given by

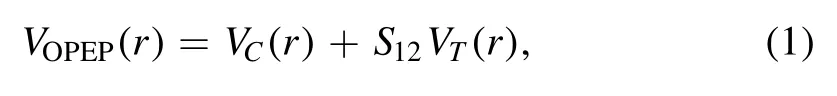
where r is equal to the length of the vector r connecting the two nucleons and S12is tensor operator.The first term in the OPEP is the central potential

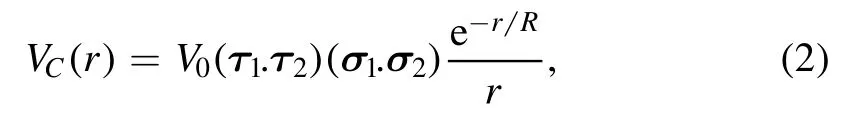
and,

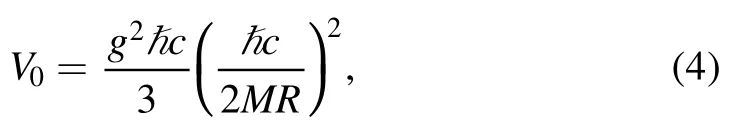
where E0is energy ground state of deuteron,m is the reduced mass of proton-neutron system and u(r)and ω(r)are the radial wave functions of13S1and13D1states,respectively.Because of the centrifugal potential, u(r) and ω(r) have different asymptotic behavior at large distances,.Furthermore,at short distances the same centrifugal barrier guarantees (at least for non-singular potentials VCand VT)that u(r)is proportional to r and ω(r) is proportional to r3.Nevertheless, the OPEP presented here only for comparison.The main idea of the paper that starts from section 2.3 does not relate to solving this equation.

2.2.A unifying potential

Now we assume that u(r) and ω(r) are proportional linearly[32]

For a linear combination of13S1and13D1components, the ground state wave function of deuteron may be written as[33]

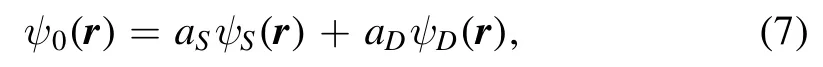
with the normalization condition

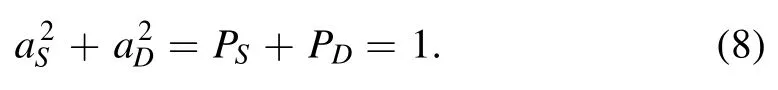
Table 2.The obtained coefficients for the potentials and superpotential for RM=R.

By replacing equations (10) in (5), we have

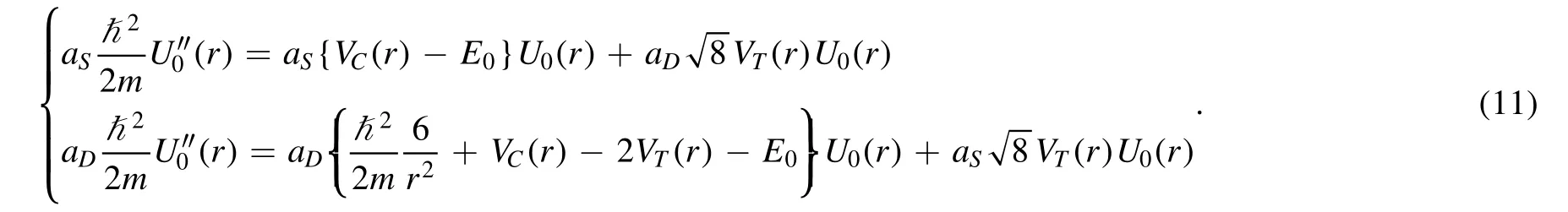
By adding these two equations, we now have an unified equation as

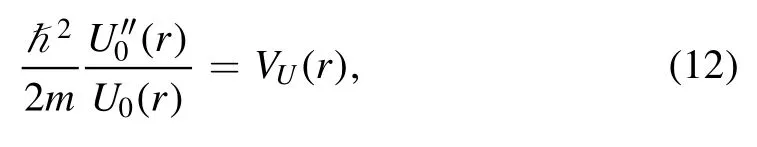
where the unifying potential is

and constant coefficients are

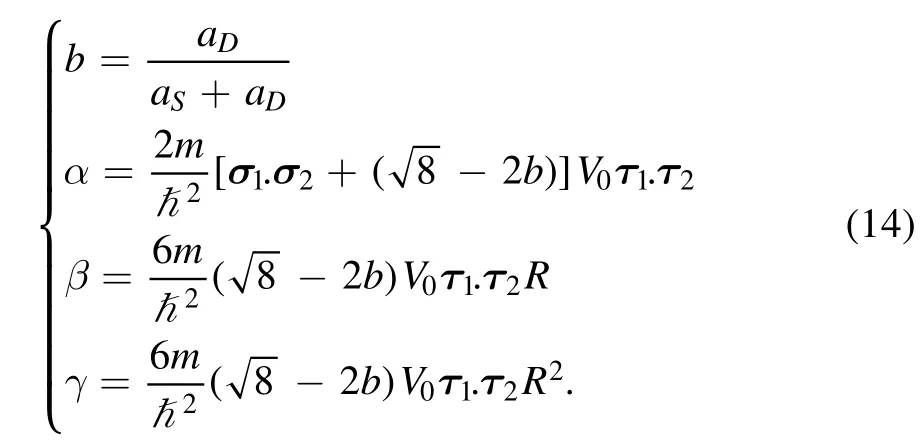
The corresponding values are listed in table 2.

2.3.Superpotential and partner potentials

In SUSY QM,by definition the superpotential as logarithmic derivative of ground state wave function [34]

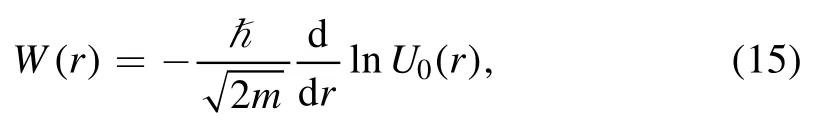
the Schrödinger equation as a quadratic differential equation is reduced to the first-order differential equation, as follows

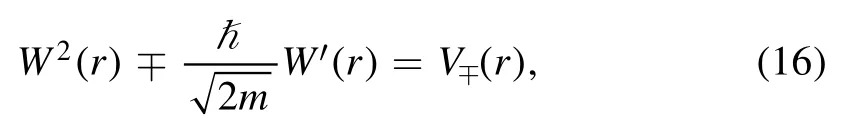
where minus and plus signs are related to V-(r) and V+(r),respectively.This equation is known as Riccati equation and V-(r) and V+(r) which are connected by the superpotential are known as supersymmetric partner potentials.

The most common way to solve this equation is to use ansatz for superpotential and to match the terms with potential via the Riccati equation [24, 35].In the same way, we now introduce an OPEP-like superpotential as follows

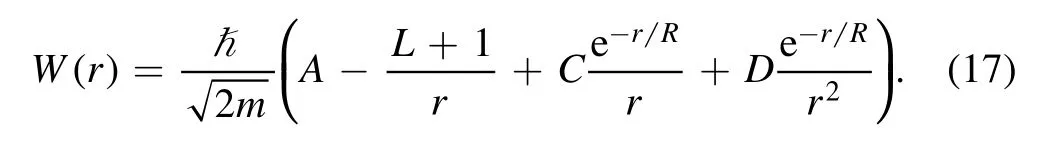
As we will see in the next section, this superpotential is designed so that it can produce the main terms of potential,amely bound energy, centrifugal potential, and pion xchange terms.The ground state wave function obtained by eplacing this superpotential in equation (15) is equal to

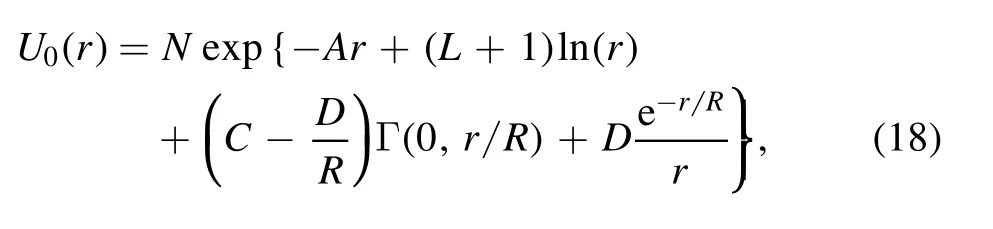
where the normalization constant N is acquired byand A,L,C and D are parameters to be determined by deuteron ground state properties in the next section.The superpotential W(r) generates partner potentials via equation (16) as

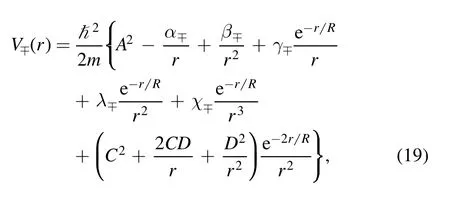
where its parameters are,

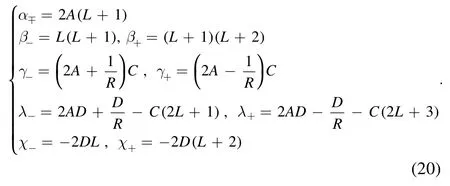
The obtained values are listed in table 2.

3.Determination of parameters

In order to determine the six constants A,aS,aD,L,C and D,we need six equations provided by using the static properties of deuteron ground state, as follows:

3.1.A

According to the unbroken SUSY,the ground state energy of V-(r) should be zero.Hence, the constant term in equation (19) is proportional to the ground state energy as

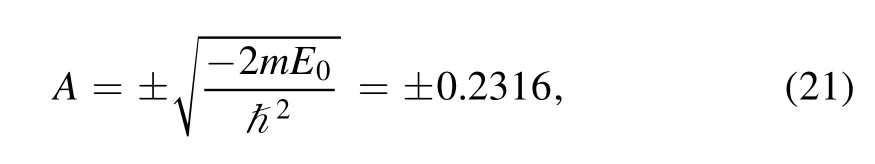
here we use experimental value for deuteron ground state energy E0(table 1)[36].The plus sign is a valid selection for A because the minus sign does not satisfy asymptotic condition (l imr→∞∣U0(r)∣2≪1) for a bound state.

3.2.aS and aD

The deuteron electric quadrupole moment is determined from the wave functions [31]

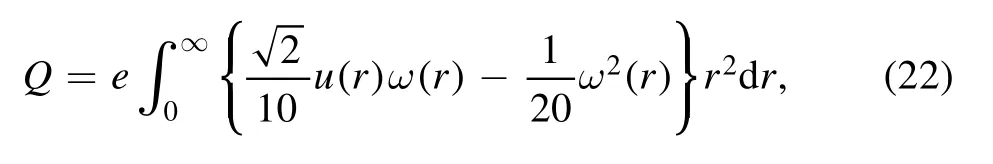
by using equation (10), we have

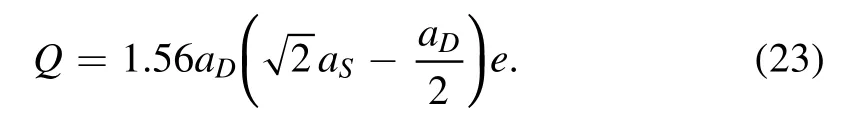
We choose to use the empirical value for the deuteron quadrupole moment (table 1).By solving simultaneous two linear equations (23) and (8) the two coefficients aSand aDare determined.

3.3.Effective angular momentum L

The third term in V-(r)is the centrifugal potential that always appears when we deal with the spherical coordinate system.The expectation value of the square of the angular momentumwith |ψ0〉 equation (7) is equal to 6ħ2PD.As a result, by the following equality

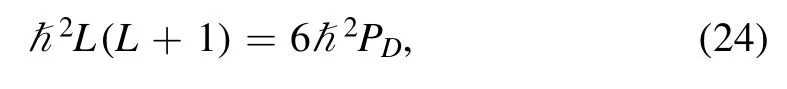
we find an effective angular momentum as

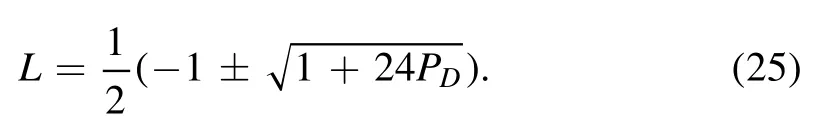
The plus sign is acceptable for a real angular momentum.

3.4.C and D

3.4.1.Wave function maximum.If deuteron has at least one bound state,its wave function should have a maximum inside the potential well.By assuming the maximum probability takes place at r=RM, we have

for special case RM=R an analytical expression obtain

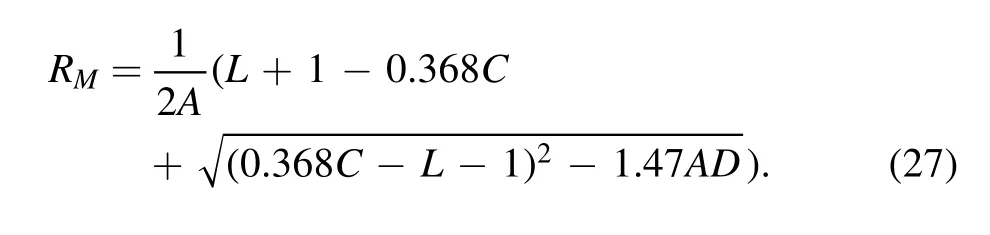
However,from equations(26)and(17)the general expression C in terms of D is as follows

3.4.2.Structure radius.The deuteron structurerstrand charge radius rd,were recently determined to use several Lamb shift transitions in muonic deuterium which in by three times more precision than previous measurements (table 1) [37, 38].On the other hand, deuteron structure radius as a characteristic deuteron size is defined from wave function,theoretically[31]

By putting equations (10) in (29) and using equation (8), the following equation is obtained

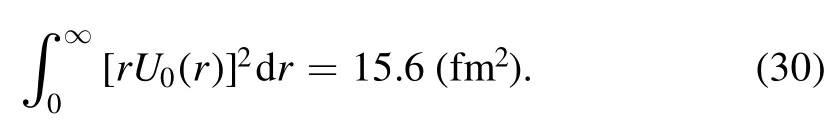
Figure 1 illustrates D for different values of RMobtained by numerical integrations resulting from the replacement of equations(28)into(30).We fit an exponential function on the result as

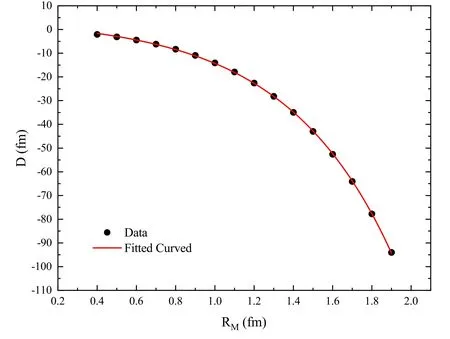
Figure 1.D versus RM.

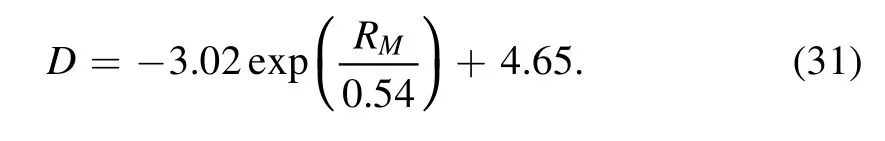
By changing the C and D with RM,the normalization constant is also changed.We have performed a similar process for it,and the results of are shown in figure 2, and the fit of its exponential function is as follows:

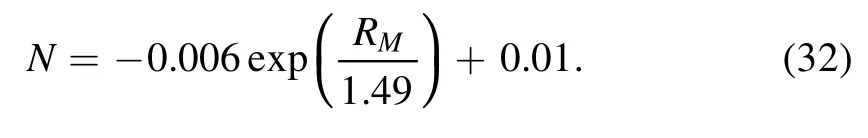
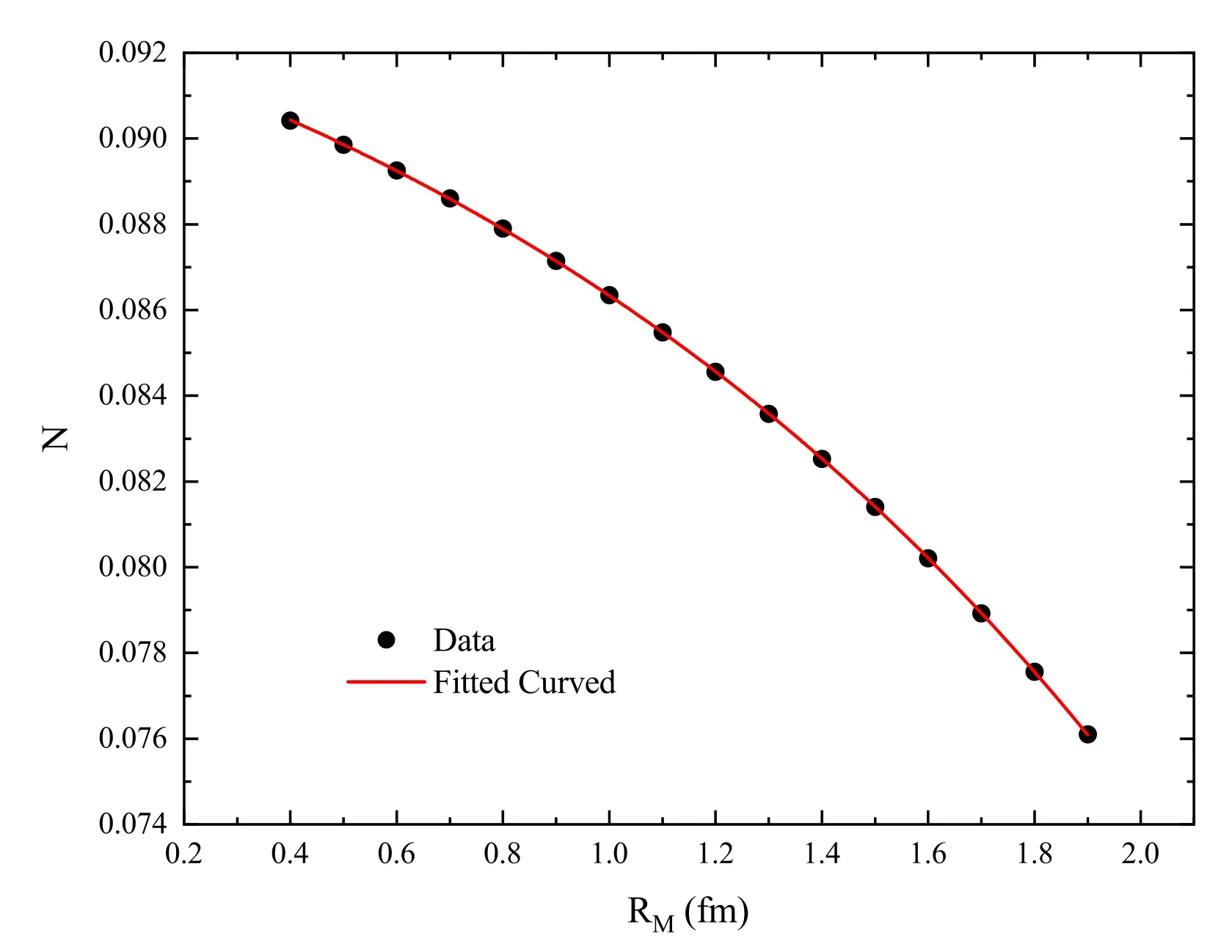
Figure 2.Normalization constant versus RM.

4.Results and discussions

In unbroken SUSY, the two quantum systems described by supersymmetric partner potentials (superpartners) have the same energy spectra except for the ground state of V-(r)[24].The ground state energy of V+(r) is equal to the first excited state of V-(r) and as a result V+(r) has one less energy level than V-(r).From figure 3,it is seen that V+(r) does not have any attractive well and thus bound states.This implies deuteron that is described by V-(r) is a weakly bound nucleus without any excited bound states [33].Furthermore, the superpartners are not shape invariant, thus we cannot obtain an analytical solution for V+(r) [35].

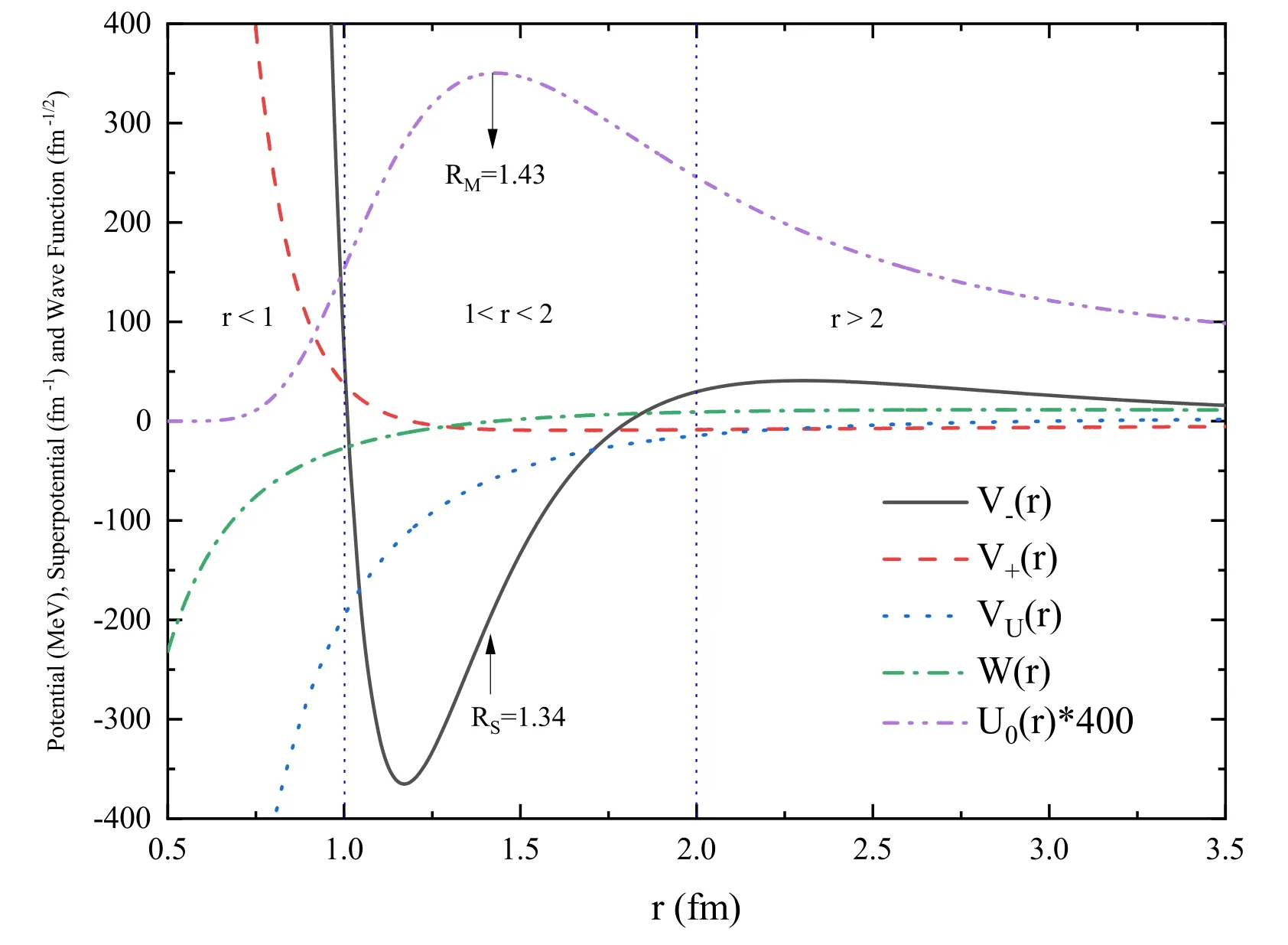
Figure 3.This figure illustrates the partner potentials V-(r), V+(r), unifying potential VU(r), superpotential W(r) and deuteron ground state wave function U0(r) for RM=R.

According to equation (15), normalizability of the ground state wave function U0(r)implies that W(r)must have a positive value as r →∞and have a negative value as r →0 [24].As a result, to ensure the existence of a zero-energy state and the presence of supersymmetry,the function W(r)must have an odd number of zeros on the real axis.Using table 2,since two values A=0.2316 and L+1-C-D=10.1729 are both positive,the superpotential equation (17) satisfies essentials in two asymptotic situations, i.e. limr→∞W(r) ≈A＞0, and limr→0W(r) ≈- (L+ 1 -C-D) /r＜0.Figure 3 also demonstrates that the superpotential W(r) has one zero on the real axis.

The NN interaction is usually classified into three main regions [33].At short separation distances (r ≤1 fm) that is so-called hardcore, it is repulsive due to the Pauli exclusion principle of identical fermions and incompressibility of nuclear matter [39].Similar to Van-der-Waals force in diatomic molecules, saturation property is due to particle exchange as well as strongly repulsive forces at short distances.It means that the nuclear force becomes repulsive when the nucleons try to get too close together.On other hand, at the intermediate-range (1 ≤r ≤2 fm), the NN potential well is attractive and causes creation bound states.Finally, the OPEP and centrifugal potential are dominated at the long-ranges r ≥2 (fm).In addition, in the asymptotic region(r →∞),the potential vanishes due to the finite range of the nuclear force between nucleons.Figure 3 shows that the potential V-(r) satisfies expected behavior in whole three mentioned regions.To make a comparison, the potentials VU(r)and superpotential W(r)are also depicted in figure 3.It can be seen that all potentials have the same asymptotic behavior limr→∞V(r) →0at the long ranges.Among them,only V-(r) satisfies the intermediate and short ranges conditions.

The ground state wave function of deuteron U0(r)(400X magnification) is plotted in figure 3.At the short ranges, the wave function is dropped rapidly due to the repulsive core.The peak of the wave function is located at the intermediate range, near the edge of the well.It is evidence of a weakly bound state within the potential well.Ultimately, the wave function decreases at the long ranges gradually.

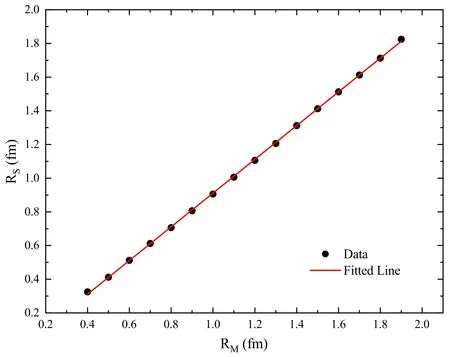
Figure 4.Potential saddle point radius RS and maximum probability radius RM.

The wave function peak radius RMis surprisingly proportional with the saddle point radius RSof the V-(r)(figure 4).We fit a line on the resulted data as

This means regardless of the value of RM, the maximum probability of the presence of particles takes place near the well edge where the potential concavity sign is changed.

Let us now compare the new potential V-(r) (created by the superpotential) with VU(r) (created by the OPEP).It is clear that V-(r) contains two more terms than VU(r), as follows

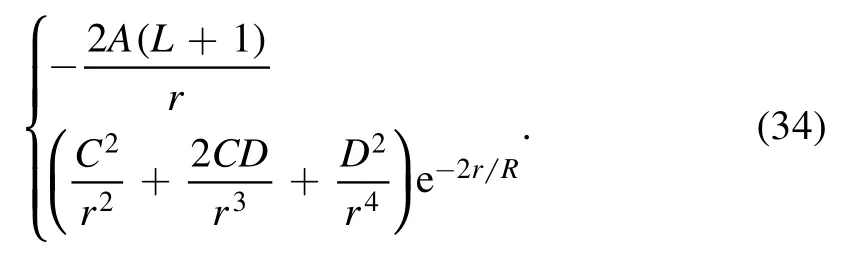
The first one is due to Coulomb potential and the second term is related to two-pion exchange potential.It should be noted that these terms do not add to V-(r)by hand but are produced by the superpotential.Since 2A(L+1)＞0,the Coulomb term implies an electric dipole moment (EDM) for deuteron [40].A permanent deuteron EDM can arise,because a CP-violating neutron–proton interaction can induce a small13P1admixture in the deuteron wave function, which should be considered.As seen from figure (3), although this fact is more prominent at the shorter distances,this term has a negligible contribution to the other components of the potential.Therefore, does not have significant impact on practical applications at low energies.

Numerous studies have shown that one boson exchange potentials(OBEP)are much easier to analyze than multi-meson ones.Therefore,in most models,the multi-pion processes have been considered as the exchange of one combined boson,rather than of multiple pions.To describe the attractive forces in the intermediate range, OBEP models need a roughly 600 MeV 0+scalar boson.In fact, many OBEP models use both a 500 MeV and a 700 MeV scalar bosons.The existence of such scalar resonances has never been accepted.In this range, two-pion exchanges dominate.In such exchanges, two pions appear during the course of the interaction.The typical range is correspondingly smaller than for one-pion exchanges.Two-pion exchanges are much more difficult to crunch out than one-pion ones.However, the superpotential W(r), simply produces a two-pion exchange term.

5.Conclusion

The most famous phenomenological models of the NN interaction (e.g.CD-Bonn, Reid93 and AV18) are based on the exchange of bosons and have many free parameters to be fitted with the experimental data[21–23].In all models,the depth of the potential is well inversely proportional to the potential width.Moreover, each channel has its specific potential.At the present unified picture, in contrast, V-is inseparable to13S1and13D1parts.As a result, the potential V-is narrower and deeper than those obtained by the other models.In addition, the13D1state probability, PD(2%–5%),is close to the lower limit.These probabilities should be recalculated due to the small13P1admixture.

Actually, the model has been presented in this paper is a phenomenological model obtained by the superpotential approach.This new attitude has introduced a new superpotential and a corresponding effective potential (V-(r)) for deuteron, as follows

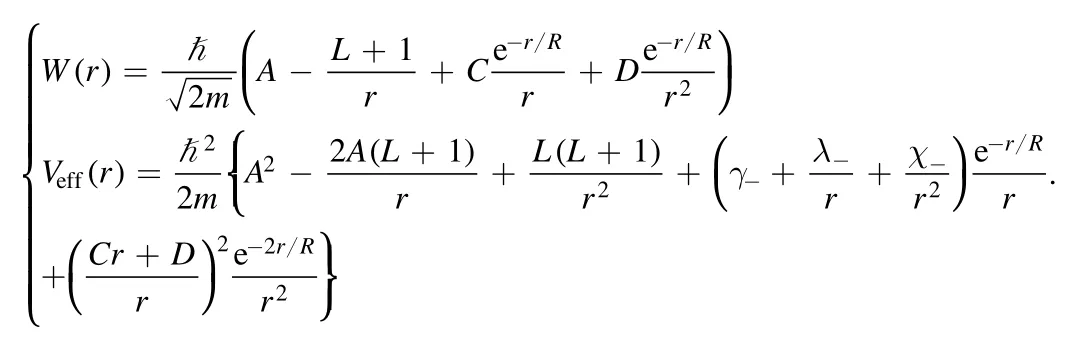
These expressions satisfy different static properties of force between nucleons, such as repulsive core at the shortrange, attractive at the intermediate range, finite range, spin and isospin dependencies,central and tensor parts,EDM,and one-and two-pion exchanges.Also, some static properties of deuteron are satisfied by the superpotential including unitary and normalization, wave functions, probabilities, binding energy,charge radius,quadrupole moment,and the existence of a weakly bound state as well as the lack of any excited states.Nevertheless,many questions about NN interaction are still unanswered, such as magnetic moment, aspect ratio,scattering length, effective range, phase shifts, locality and non-locality properties, energy and momentum dependencies of NN interaction, etc.

Acknowledgments

The present study was carried out during T K’s sabbatical stay at Istanbul University.The authors acknowledge the financial support from Golestan University and Istanbul University.

ORCID iDs