地壳均衡理论及其在构造地貌研究中的应用

舒远海，石许华，陈汉林，杨蓉，林秀斌，程晓敢，吴磊，龚俊峰，邓洪旦，白卓娜，王锦涵

浙江省地学大数据与地球深部资源重点实验室，浙江大学地球科学学院，杭州，310027

内容提要: 地壳均衡是地球科学的一个基本概念，其理论基础为“轻地壳(密度较小)漂浮在重地幔(较稠密)之上”。均衡理论(如冲压假说、弹性板理论等)和模型(如Airy模型、Pratt模型及弹性板模型等)的产生及发展对研究岩石圈流变学性质、圈层相互作用及造山作用等地球动力学过程有着重要意义。本文总结了相关均衡理论、模型及计算方法，并结合其在不同空间尺度构造地貌现象研究中的运用，包括：① 冰川均衡调整研究中不同模型的优化及其对全球海平面变化的指示意义、② 阐明海山洋岛发育过程及其制约因素、③ 利用弹性板模型重建山脉隆升和盆地挠曲沉降史并进一步探讨二者之间的相互作用、④ 通过研究变形湖滨线有效地约束地球的相关物理参数、⑤ 建立河流三角洲发育特征模型并服务于现代社会经济、⑥ 揭示水库蓄水导致的地壳挠曲变形与浅部地质灾害发育的关系及 ⑦ 同震滑坡对局部地貌改造的影响，讨论并展望了未来地壳均衡在构造地貌学领域的发展方向，即结合高精度大地测量技术与地质年代学方法，定量地解决构造地貌研究中的关键问题，更全面、系统地了解地表过程、地球深部过程与动力学和地球圈层之间的相互作用。

地壳均衡(isostasy)来源于希腊单词“iso”和“stasis”，意为“equal standing”；均衡理论揭示地壳和地幔在没有干扰力的情况下趋向于均衡状态。冰原的消长、侵蚀、沉积和火山喷发等地表活动破坏了地壳均衡，地壳和地幔会对此做出相应的反应调节，进而影响深部动力学及地表过程。这些反馈过程及方式与岩石圈的物理流变学性质密切相关。因此，地壳均衡过程受控于地球外部圈层的物理性质及其相互作用，是地球系统科学研究的一个重要组成部分，可用于约束岩石圈的物理性质，并理解复杂的地球动力学现象(Watts，2001)。

均衡思想理论的提出和发展经历了近170年的历程。达·芬奇于15世纪后半叶提出了关于地球外层平衡的最初想法(McCurdy，1928；Delaney，1940)；19世纪中叶，Airy(1855)和Pratt(1858)经典均衡理论及模型相继诞生；19世纪末至20世纪初，对均衡本质的认识导致人们不再认为均衡补偿是浮选或差异冷却的结果，而是由地形形成过程决定(Fisher，1882；Dutton，1892；Meinesz，1941；Bagherbandi et al., 2013)；20世纪30年代，出现了偏向Pratt模型的美国学派和偏向Airy模型的欧洲学派(Hayford，1909；Heiskanen，1931)；20世纪40～50年代，地震观测结果(大陆地壳比大洋地壳厚)与Airy模型的预测一致(Watts，2001)。现代均衡观点认为，地球外层具有有限强度，能够支撑长地质时期的载荷(Watts，2001)。

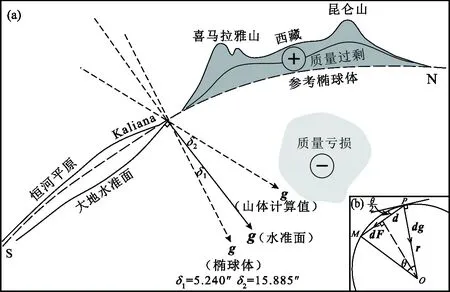
图1 垂线偏转测定示意图Fig. 1 Schematic diagram of the measurement of the vertical deflection(a) 印度北部Kaliana地区的垂线偏转量，δ1为根据天文和大地观测得到的由珠穆朗玛峰引起的偏转(天文位置定义为赤道面与当地铅垂线方向之间的夹角；大地位置定义为赤道面与地球最佳拟合椭球的局部法线之间的夹角)， δ2为Pratt根据海平面以上喜马拉雅山、西藏和昆仑山的质量过剩所计算的偏转(Watts, 2001)；(b) Pratt对M点处质量为dm的物体在P处产生的万有引力dg的测定，计算公式为(a) The vertical deflection in the Kaliana region of northern India. δ1 is the deflection caused by Mount Qomolungma based on astronomic and geodetic observations (the astronomic position is defined as the angle between the equatorial plane and the direction of the local plumb-line, and the geodetic position is defined as the angle between the equatorial plane and the local normal of the Earth′s best-fitting ellipsoid). δ2 is the deflection calculated by Pratt according to the mass surplus in the Himalaya, Xizang(Tibet) and Kunlun Mountains above sea level (Watts，2001). (b) Pratt′s measurement of the gravitational attraction, dg, at a station P due to a mass dm at M. The calculation formula is (Pratt，1855)

近几十年来，由于地球系统科学研究理念的不断深入，地壳均衡理论在构造地貌学研究中得到广泛应用。20世纪90年代以来，关于气候变化、剥蚀和构造过程之间互馈作用的研究(Molnar and England，1990；Raymo and Ruddiman， 1992；Molnar et al., 1993，2015)大力加强了地球科学界对地壳均衡理论及其应用的关注。Molnar和England(1990)认为，气候变化、风化、侵蚀和均衡反弹可能在一个正反馈系统中互相影响：侵蚀速率的增加和均衡反弹会导致山脉的隆升，从而影响气候、进一步加强侵蚀；而侵蚀后的均衡反弹又会进一步导致山脉的隆升、再次影响气候。该观点引发了后续几十年一系列关于地表过程与深部构造之间相互作用的研究。此外，地壳均衡被广泛应用于不同空间尺度的研究中，比如全球范围内的冰川均衡调整、大型海山洋岛形成过程、山脉隆升和盆地挠曲沉降史、大规模湖滨线变形与河流三角洲发育特征，以及水库变形和同震滑坡对局部地质灾害发育、地貌演化的影响。

基于地壳均衡理论的重要性，本文总结该理论的提出与发展历史、前人对地壳均衡理论、模型及计算方法的认识，以及在构造地貌学研究中的运用，然后讨论已有均衡研究存在的局限性，展望了未来均衡理论、模型及其在构造地貌应用中的发展方向。

1 均衡理论及模型的发展

有关地球外层处于平衡状态的最初想法来自于达·芬奇，他于15世纪后半叶对地球如何响应其表面载荷的变化进行了思考，认识到从山上移走沉积物可能导致山脉隆升(McCurdy，1928；Delaney，1940)。约200年后，对于地球形状的首次关注有力推动了对山脉平衡状态的研究，这些研究也促使曾主导欧洲地质学思想的收缩理论的诞生(Watts，2001)。不同学派对于收缩理论的讨论促进了早期均衡思想的发展。而后，对于印度地区子午线长度的测量(Everest，1857)提升了人们对地壳均衡思想的认识，并推动了相关经典均衡模型的诞生。

1.1 关于收缩理论的讨论

19世纪早期，欧洲地质学思想由收缩理论主导。地表特征被认为是地球形成后逐渐冷却的结果，山区的冷却程度较海洋地区弱(Watts，2001)。收缩理论支持者(如：Pratt，1855，1870；Fisher，1882；Dutton，1892)认为在全球范围内，沉降和隆升是热胀冷缩的结果。Lyell(1832～33)对收缩理论持怀疑态度，认为地表处于动态变化中，反对用灾变理论来解释地质事件。Herschel(1836)反对收缩理论，提出地球最外层(地壳)及其下层(熔岩海)处于某种形式的动态平衡，沉积物载荷会引起地壳下沉，导致熔岩从载荷之下流向侧翼地区。不同学者之间关于收缩理论的讨论推动了早期均衡思想的发展，为了解地壳均衡的又一个重大进展——垂线偏转的发现——奠定了理论基础。

1.2 垂线偏转的发现

Everest(1857)在绘制相关地图期间发现恒河平原上两个站点之间用大地测量方法计算得到的纬度差比用天文法得到的小5.24″。Pratt(1855)认为这种差异是由于附近喜马拉雅山的干扰效应造成的，并通过万有引力定律计算出其可使铅垂线偏转15.885″(铅垂线偏离当地法线的量称为垂线的偏转量)，是观测值的3倍多(图1)。该项工作从实测的角度验证了物质分配的不均匀性，后来被认为是地壳均衡的第一个观测证据(Putnam，1929)。

1.3 地壳均衡模型

对于物质分配在水平方向和垂向上不均衡性的发现及研究，促使了经典均衡模型——Airy模型和Pratt模型的诞生。地壳均衡本质的提出及改进后的均衡模型提供了可用于大地测量计算的有效方法，极大地促进了均衡理论的发展及应用。

1.3.1Airy和Pratt均衡模型

Airy(1855)解释了采用大地方法与天文方法进行测量所得结果存在差异的原因，基于对“地球外层由一层薄地壳组成，覆盖在密度较大的流体层之上”的简单物理观点的认同，通过与冰山的类比，提出一个升高的区域(如高原)下面是一个密度较低的区域(“轻地壳”代替“重熔岩”)(图2a)。

Pratt(1858)遵循Airy关于质量盈亏的观点，通过精细的数学计算提出了关于地球外层平衡的模型；认为地表的低洼区和隆起区是热胀冷缩的产物，前者被高密度岩体所覆盖，后者被低密度岩体所覆盖(图2b)。

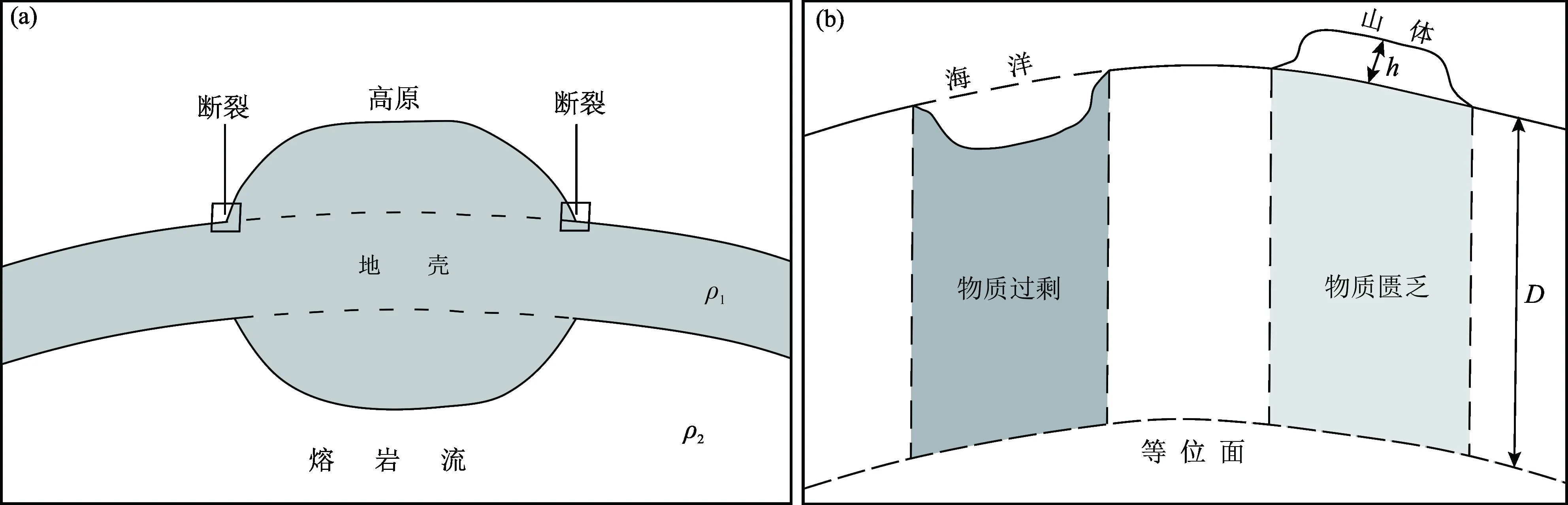
图2 Airy和Pratt均衡模型示意图Fig. 2 Isostatic models of Airy and Pratt(a) Airy均衡模型：一个广阔的高原不太可能被任何方式支撑，除非其下部是突出到“熔岩流”中的低密度地壳(ρ2>ρ1)，“断裂”会在高原的边缘形成(Airy, 1855)；(b) Pratt均衡模型：山体被低密度物质覆盖，洋底被高密度物质覆盖，在等位面上两者质量相等(h为山体高度，D为补偿深度)(Pratt, 1858)(a) Airy′s model: A wide table-land is unlikely to be supported in any way, unless by a lower density crust that protruded into the underlying “lava"(ρ2>ρ1). The “breakages” would form at the edges of the table-land (Airy, 1855). (b) Pratt′s model: Mountains are underlain by low-density materials while oceans are underlain by high-density materials. Masses are equal at the depth of the equipotential surface(h is the mountain height, and D is the depth of compensation)(Pratt, 1858)

1.3.2Fisher均衡模型

Fisher(1882)并没有过多地关注Airy模型和Pratt模型之间的争议，而是反驳收缩理论，他抓住了地壳均衡的本质——地壳遵循阿基米德原理(漂浮在液体中一块物体的重量等于其排开液体的体积)。Dutton(1892)支持其观点，认为如果地球是由均匀物质组成的，其平衡体将是一个旋转椭球体。但是，如果存在密度差异，平衡体形状将发生变化，地壳会在低密度物质堆积的地方呈现上凸的趋势；在高密度物质堆积的地方呈现下沉的趋势。他意识到地壳均衡是一个朝着平衡方向发展的过程，对地壳有一定程度的“保护”作用，使其不受大幅度升降活动的影响。

1.3.3Pratt-Hayford和Airy-Heiskanen
均衡模型

Airy模型和Pratt模型是基于不同均衡补偿特征而提出的概念模型，并不能用于定量的大地测量计算。

Hayford(1909)改善了Pratt模型，减少了重叠调查之间、大地位置和天文位置之间的差异。已知山体下岩石柱底部的压力Pl、海岸下岩石柱底部的压力Psc分别为：

Pl=Dρlg+hρscg

(1)

Psc=Dρscg

(2)

由地壳均衡可得：

Dgρl+hgρsc=Dρscg

(3)

(4)

(5)

其中，ρl为山体底部岩石柱的密度，h为山体高度，ρsc为海岸地壳密度，D为补偿深度，ρ0为海底岩石柱的密度，ρw为水的密度，wd为水体深度。假设ρsc=2670 kg/m3，D=113.7 km，ρw=1030 kg/m3，由(4)及(5)式可知，高出海平面3 km的区域下的平均密度比海平面下低约3%；低于海平面5 km处的区域下的平均密度比海平面下要高出约3%(图3a)。

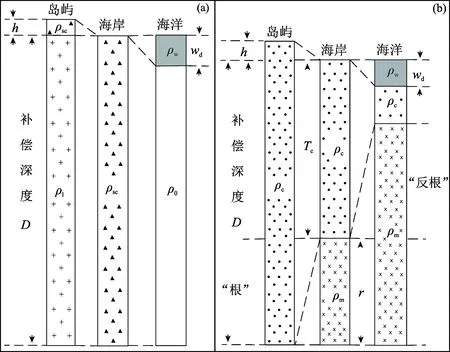
图3 两种改良后的均衡模型: (a) Pratt-Hayford均衡模型(Hayford, 1909)；(b) Airy-Heiskanen均衡模型(Heiskanen, 1931)Fig. 3 Two modified isostatic models: (a) the model of Pratt-Hayford (Hayford, 1909); (b) the model of Airy-Heiskanen (Heiskanen, 1931)

图4 Bowie用漂浮在水银中的金属块对均衡模型的图解(Bowie, 1927): (a) Airy模型; (b) Pratt模型Fig. 4 The Bowie′s illustration of the Pratt and Airy′s models using metal blocks floating in mercury (Bowie, 1927)(a) Airy model; (b) Pratt model

Heiskanen(1931)对Airy模型进行了相关改善，推导出：

Pl=(Tc+h+r)ρcg

(6)

Psc=Tcρcg+rρmg

(7)

由地壳均衡可得：

Pl=Psc

(8)

(9)

其中，Tc为地壳厚度，r为地壳向地幔内凸出的深度，ρc为地壳密度，ρm为地幔密度。假设ρc=2670 kg/m3，ρm=3300 kg/m3，由(9)式可得出，高出海平面3 km的山体下部的地壳会向地幔凸出12.7 km，这一部分称为“根”，海洋下部地壳相应变薄的部分称为“反根”(图3b)。

Bowie(1927)使用漂浮在水银中的金属块对Pratt模型和Airy模型的均衡特点进行了解释(图4)。Airy模型和Pratt模型表明，地质体特征(无论大小)会在局部得到补偿，补偿是通过等密度的地壳增厚(Airy模型)、等厚度的地壳密度横向变化(Pratt模型)，或这些因素的某种组合来实现的(Watts，2001)。但是，这两种模型只考虑到了柱体的垂向压力，忽视了地壳各柱体间的内聚力，故其假定的补偿是局限的(刘缵武和陆仲连，1999)。Pratt-Hayford和Airy-Heiskanen两种均衡模型提供了在全球范围内测量地壳均衡程度的方法(Watts，2001)，它们从各自的角度反映了地球内部真实的质量分布情况，而实际的地壳均衡模式应为两者按一定比例结合的成果(邢健等，2014)。Meinesz(1931)受Putnam关于区域补偿观点的影响提出了区域均衡说，以区域性补偿代替局部补偿，把地形看作导致地壳挠曲的地表载荷，修改了Airy-Heiskanen模型。

均衡理论及模型的不断发展及丰富引发了后期对于均衡调整程度及地球外层强度的研究。一系列实验室及自然界中的实验不断完善相关模型所忽略的地球外层具有有限强度的概念。不同模型下均衡计算方法的提出将理论模型应用到实际，量化了均衡调整的程度及地球外层的强度。

2 均衡实验与计算

Pratt-Hayford模型和Airy-Heiskanen模型对于均衡计算的量化具有重要意义，尤其是在对地球形状的研究中。另一方面，这两种模型提供了在行星尺度上测试均衡作用程度的方法，其中一个重要的测试是计算模型的引力效应，并将其与地球重力场的测量值进行比较；另一个测试是通过冰川均衡反弹及其引起的海平面变化的研究提供壳幔物理性质及均衡产生的时间尺度等关键信息。与此同时，对于具体地质现象、均衡补偿参数、岩石圈强度及均衡响应函数等的计算又一次促进了相关理论及模型的诞生及发展。

图5 “冲压假说”对冰川消融地区隆升和沉降的解释(Daly, 1935)Fig. 5 The explanation of “viscous bulge” hypothesis to the uplift and subsidence of a deglaciated region (Daly，1935)

2.1 布格异常及均衡异常的测定

重力场取决于地球的形状和内部质量的分布，而地壳均衡涉及地壳物质的调整，因此重力场偏离地球地形模型的预期值及其补偿值可表明达到均衡的尺度(Watts，2001)。

(1)布格异常(Bouguer Anomaly)。Putnam(1895)利用“平均海拔均衡降低法”，消除了重力测量中的较大误差；在修正了地球扁平率及旋转和质量分布的影响后得出：

BA(布格异常)=FAA(自由空气异常)-BC(布格校正)

Putnam(1895)认为，一般的大陆高地由低于海平面的物质的质量密度不足而得到补偿，但因局部地形的不规则性没有被完全补偿，而是由局部地壳强度支撑。

该研究是地壳均衡概念发展的一个重要里程碑，是有关大陆地区地壳均衡程度的最早认识之一，也是第一个暗示地壳均衡可能不是在所有地方都存在(Watts，2001)。

(2)均衡异常(Isostatic Anomaly)。Hayford(1909)使用Pratt模型对Putnam的方法进行细化后得出：

IA(均衡异常)=FAA-BC-IC(均衡校正)

Hayford(1909)发现，均衡异常的大小提供了对区域补偿程度评价的某种度量。小幅度均衡异常表明地质特征处于某种形式的均衡；大幅度异常表明地质特征要么部分补偿，要么未得到补偿。

2.2 冰川—地壳均衡说与冲压假说

Daly(1935，1939)基于对Airy均衡模型的认识，通过对北美地壳在更新世冰川作用下升降过程的研究，认为均衡状态会在冰川长期加载于地壳之上时产生。冰川消融破坏了均衡，释放大量的水到周围的海洋，地壳和上地幔均衡状态的调整以适应冰川载荷的转移是“冰川—地壳均衡说”的主题。他通过对大型冰原升降模式的研究，提出了“冲压假说”：冰川加载时侧翼区被下拉，但由于底部物质的侧向挤出最终抬升；冰川卸载时侧翼区抬升，但由于物质回流最终下沉(图5)。Daly对“冰川—地壳均衡说”的研究提供了关于地壳均衡的两项重要信息——地幔提供应力的大小和地壳均衡调整发生的时间尺度(Watts，2001)。

2.3 海岸线高度的测量

Bloom(1967)扩展了早期Daly等冰川均衡的工作，结合Airy-Heiskanen均衡模型研究以往海岸线高度，测试了地壳均衡及其可能发生的时间尺度。海平面变化时海岸上第2个海蚀刻痕的位置取决于地壳因卸荷或负荷时均衡调整的速度(缓慢调整时，首先在低于海岸线S1点h高度的S2处形成刻痕，然后在高于S2点y距离的S3处形成刻痕；快速调整时，海平面将直接达到S3处，不会在S2处形成刻痕。)；他假设海洋中的一根柱子在卸荷前后处于局部均衡状态，计算出了新旧海岸线之间的高度差(图6)。

由hρwg+wdρwg+Tcρcg=wdρwg+Tcρcg+yρmg可得：

(10)

假设ρw=1030 kg/m3，ρm=3330 kg/m3，由(10)式可知，如果海平面下降高度h=108 m，洋盆将抬升y=33 m。如果抬升速度比下降慢，则新旧海岸线之间的高度差为108 m；如果抬升速度较快，则为h-y=75 m。

图6 海平面及其与慢速和快速均衡调整的关系示意图(据Bloom, 1967)Fig. 6 The sea level and its relationship to slow and fast isostatic adjustment (from Bloom，1967)

从最后一次冰期和间冰期历史可知，海平面可以在相对较短的时间内出现升降变化；来自海岸线的数据表明均衡调整是迅速的，基本上可以在几万年内完成(Watts，2001)。

2.4 均衡计算

在上述均衡实验中涉及到对于具体地质现象所反映的地壳均衡程度、相关均衡补偿参数、岩石圈强度及均衡响应函数等的一系列计算，这里做简单概述。

Gilbert(1889，1890)用Airy模型来计算因博纳维尔湖(Lake Bonneville)水位下降而引起的地壳隆升，从计算值大约是观测值2.5倍的结果中意识到地壳的内在强度对隆升的抵抗作用。Putnam(1912，1929)提出区域补偿的概念，认为区域补偿面积的增大减小了均衡异常差异；区域补偿相当于能够承受巨大载荷的地壳强度(即区域补偿与地壳强度的联系)。Meinesz(1931)把地形看作是一种会导致地壳挠曲的地表载荷，如果载荷足够大，将迫使坚硬的地壳向下伸入下垫层，形成一个类似于Airy模型预测的低密度“根”；载荷中心至挠曲度为零的距离被称为区域半径(R)。Gunn(1937，1943，1944)提出地表特征是由区域地壳均衡所支持的，并测试了岩石圈强度在解释偏离局部地壳均衡模型时可能发挥的作用，认为控制某一地质特征补偿程度的主要因素取决于载荷的宽度和下垫板的弹性特性，首次系统地测试了区域地壳均衡程度。Walcott(1970a，b)第一次精确地测定了板块的刚性以及其力学性能在时空上变化的程度；研究得出板块内部大载荷区地壳有效弹性厚度(Te)在5～114 km范围内，弹性厚度取决于载荷的年龄。Dorman和Lewis(1970)在传统使用均衡响应函数(由假定的补偿机制推导而来的地球重力场对点载荷的响应)进行均衡还原计算的基础上，给出了直接从观测数据计算该函数的方法，消除了对补偿机制的假设。

上述对于均衡的实验与计算结果在产生及发展过程中互相促进、补充，提供了用于检验单一特征地质体达到均衡程度的简单方法。但是，大多数早期的模型认为地壳是软弱的，并没有考虑到其具有弹性特征(Gunn，1949)。基于“岩石圈是一个坚硬且均匀有弹性的板块，被下部强度较弱的软流圈所支撑”的假设的弹性板模型提供了用来比较各类地质和地球物理观测结果的“参考”模型，被广泛应用于研究不同地质体的特征、形成过程及相互关系中(Watts，2001)。因此，有必要对弹性板模型进行相关介绍。

3 弹性板模型

弹性板理论认为：地壳和上地幔在其上覆载荷的加载及卸载过程中会表现出均一的弹性性质。尽管弹性板块模型在一定程度上简化了地壳和地幔在长时间尺度地质过程中的行为方式，但它提供了一种比较实用的、用于对比各类地质和地球物理观测资料的“参考”模型，并可以很好地近似模拟岩石圈在大型载荷作用下产生挠曲变形的情况(Watts，2001)。

3.1 弹性板模型简述

弹性板模型主要包括：

(1)线性弹性模型。该模型假设弹性板在挠曲变形过程中产生的应力与应变呈线性比例关系。这种假设在简化了数学计算的同时允许使用叠加法则(总的挠曲变形量可等效为单位载荷所产生变形量的叠加)。因此，在右旋正交笛卡尔坐标系中，主应力(σ1，σ2和σ3)和主应变(ε1，ε2和ε3)可通过相应拉美参数建立线性关系，为研究岩体力学性质及受力情况分析等提供了参考(Jaeger，1969；Watts，2001；图7a)。

(2)柱形弯曲模型。如果弹性板的长度是其宽度的3倍，那么在其边缘被加载时，将产生柱形弯曲(Timoshenko，1940；图7c)。在该过程中，弹性板的任何变形都局限于其最边缘部分，这就意味着可能没有必要使用一整块弹性板来模拟地壳和地幔的变形情况。因此，当应力和应变仅作用于研究对象局部时，可采用该模型。

(3)梁挠曲模型与Winkler地基模型。梁挠曲模型定义了弯曲力矩及其计算公式；Winkler地基模型表明作用于该地基上每一点的应力与其产生的挠曲变形量呈正比，并结合弯曲力矩的计算公式，推导出覆盖在无粘性基底之上弹性梁挠曲变形的一般方程(Hetényi，1979；图7b)。相关理论及模型被广泛应用于机械工程、水库大坝及铁路轨道变形等研究领域。

(4)半无限梁模型与无限梁模型。地质研究中最关心的是对于弹性梁延伸很长距离时其挠曲变形情况，而这两种端元模型考虑到了在半无限长和无限长弹性梁的一端施加载荷的特殊情况。模拟结果表明，挠曲变形量由载荷中心向延伸方向呈现出正余弦函数的指数衰减形式，体积弹性模量(λ)控制着挠曲变形曲线的波长和振幅。其中，半无限梁模型在距离线型载荷(0，π/(2λ))区间内表现为“下凹”状变形，隆起顶点位于3π/(4λ)处，在π/(2λ)处(第一个节点)无变形；无限梁模型在距离线型载荷(0，3π/(4λ))区间内呈现出“下凹”状变形，在(3π/(4λ)，7π/(4λ))区间内表现为“上凸”状变形，隆起顶点位于π/λ处，在3π/(4λ)处(第一个节点)无变形(Hetényi，1979；Watts，2001；图7d，e)。

(5)圆形板模型。在构造地貌学研究领域，圆形板模型及相关理论具有普遍适用性，目前被广泛运用于解决火山载荷变形(Watts，2001)、变形湖滨线对岩石圈流变学性质的约束(Shi Xuhua et al., 2015)、冰后期地壳均衡反弹(Mey et al., 2016)以及水库蓄水导致地壳挠曲变形(Madson and Sheng Yongwei, 2020)等问题，故在此对其进行简述。

3.2 圆形板模型

Hertz(1884)、Brotchie等(1969)及Hetényi(1979)给出了覆盖在无黏性基底上圆形板挠曲的解析解；Brotchie等(1969)推导出了弹性薄球壳产生挠曲的一般方程：

(11)

在等式(11)中，△4为在壳体表面坐标中的双调和算子，w为径向位移，q为施加的载荷，D为抗弯强度，定义为：

(12)

在等式(12)中，Te为地壳有效弹性厚度，ν为泊松比；E为杨氏模量，定义为：在横向不受限制的轴向压缩或拉伸的固体中，应力与应变的比值，其表达式为：

(13)

在等式(13)中，λ为体积弹性模量，定义为：静水压力和其所产生的膨胀的比值，其决定了变形的振幅和波长，表达式为：

(14)

ρinfill为填充物的密度；在等式(11)中，β为三维挠曲常数，可表示为：

(15)

对于一个集中载荷P所产生的径向位移w可表示为：

(16)

在等式(16)中，r为以载荷为中心的径向距离，kei为零阶Kelvin函数。

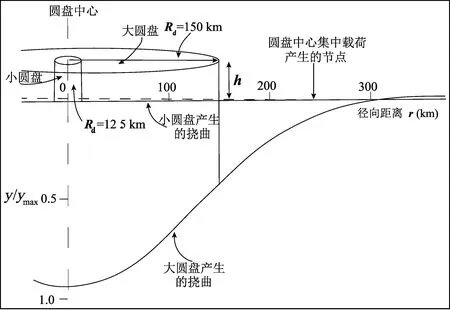
在等式(11)中，对于一个高度为h，半径为Rd，密度为ρload的圆盘状载荷所产生的径向位移w为(图8)：

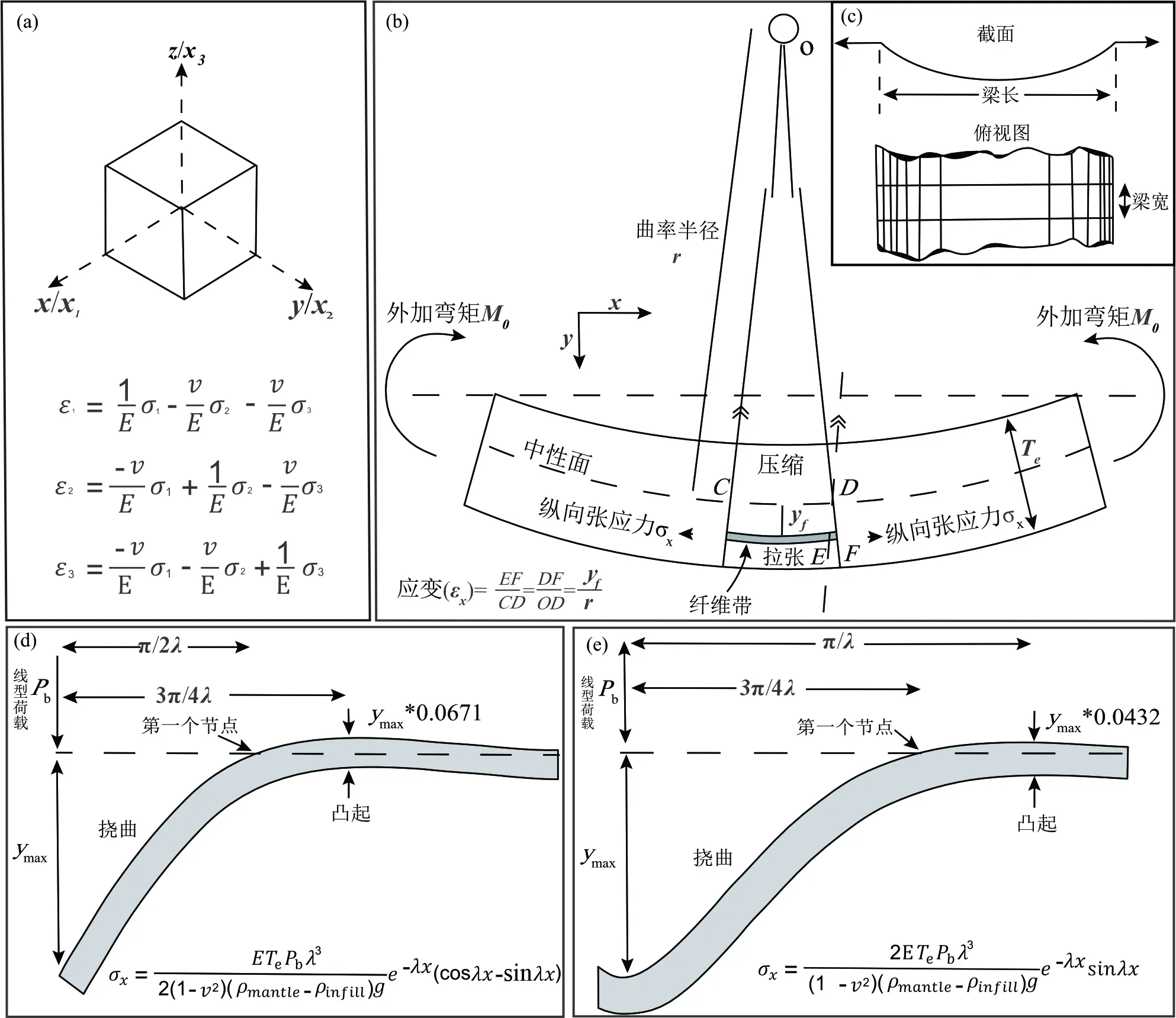
图7 弹性板模型示意图Fig. 7 The schematic diagram of elastic plate models(a) 线性弹性模型：右旋正交笛卡尔坐标系中x、y和z轴及其相对应的x1、x2和x3轴；方程表示应力与应变的关系(Jaeger，1969；Watts，2001)。(b) 弯曲力矩作用下弹性梁挠曲变形模型(Hetényi，1979)。(c) 柱形弯曲模型(Timoshenko，1940)。(d) 半无限梁模型及其上表面应力计算公式。(e) 无限梁模型及其上表面应力计算公式(Hetényi，1979；Watts，2001)。相关参数含义见章节3.2(a) Linear elastic model. The x, y and z and the alternative x1, x2 and x3 axes in right-handed, orthogonal, Cartesian coordinate system. The equations express the relationship between stress and strain (Jaeger，1969； Watts，2001). (b) Flexure of the elastic beam caused by bending moment (Hetényi，1979). (c) Cylindrical Bending (Timoshenko，1940). (d) Semi-infinite beams and computational formula for the stress on the uppermost surface of it. (e) Beams of unlimited length and computational formula for the stress on the uppermost surface of it (Hetényi，1979； Watts，2001). The meanings of the relevant parameters are detailed in Section 3.2

(17)

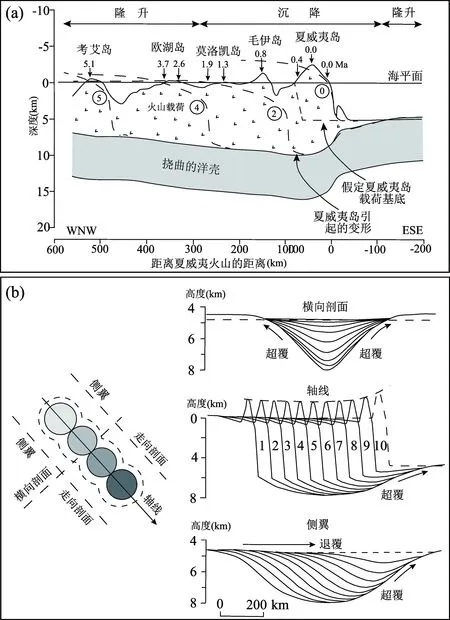
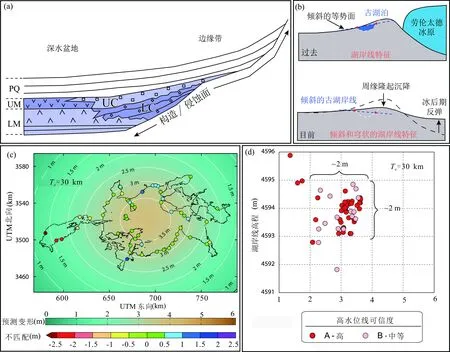
此时，产生的变形位于载荷之下，即：r

或：

(18)

此时，产生的变形位于载荷之外，即：r>Rd(Watts，2001)。等式(17)和(18)中，kei和ker，kei′和ker′分别是零阶和一阶Kelvin函数；bei和ber，bei′和ber′分别是零阶和一阶Bessel 函数。

4 地壳均衡理论在构造地貌研究中的应用

地壳均衡理论、模型及计算方法被广泛运用于地质体特征及其形成过程、岩石圈流变学性质、洋陆的演化和类地行星特征等方面的研究中；地壳均衡涉及到地壳物质的调整(地表的剥蚀和沉积是最为直接的物质调节方式之一)，同时也涉及地球外部圈层的相互作用。因此，均衡方法被广泛应用于构造地貌的研究，帮助我们定量认识地表过程、地球深部过程与动力学和地球圈层之间的相互作用。

图8 由大圆盘和小圆盘载荷产生的挠曲示意图(Watts, 2001)计算结果基于Te=20 km，ρinfill=2800 kg/m3，ρm=3270 kg/m3Fig.8 The deflection of a circular plate by narrow and wide disc loads (Watts，2001). The calculations are based on Te=20 km，ρinfill=2800 kg/m3，ρm=3270 kg/m3

笔者等按照空间尺度由大到小的顺序(①影响全球海平面变化的冰川均衡调整，②大型海山洋岛的生长过程，③山脉隆升和盆地挠曲沉降，④可用于约束壳幔流变参数的变形湖滨线，⑤河流三角洲发育特征，⑥对周边水电设施与地质灾害造成影响的水库变形和⑦对局部地貌特征具有改造作用的同震滑坡)对均衡理论在构造地貌学各领域的研究现状进行归纳总结。

4.1 冰川均衡调整

冰川均衡调整指冰川旋回期间岩石圈对其表面载荷(冰和水)再分配的动态响应，对研究地质历史时期以来全球海平面的相对变化有着重要意义。Chappell(1974)及Watts等(1978，1982，2001)对全新世海岸线变化的研究表明，地壳挠曲变形在海岸线演化过程中可能起着重要作用，冰川消融引起的海盆变形是海平面上升的主要原因。

冰川均衡调整的研究不同于均衡实验时利用单一的理论模型，基于对地球内部结构认识的深入，该研究涉及多种不同模型。多数模型的输入包括冰期—间冰期历史和岩石圈的黏弹性结构，输出包括岩石圈对冰川均衡调整做出各种响应(地表运动、地表质量分布、大地水准面的变化、重力、应力及惯性矩等)的历史。Walcott(1970c，1973)最早提出了冰原载荷作用下岩石圈挠曲的简单模型——变形从载荷下方延伸到两侧区域，凸起发育于侧翼区挠曲拗陷之后(图9)。

图9 冰原载荷作用下岩石圈挠曲模型(Watts, 2001)Fig. 9 The model of flexure of the lithosphere caused by an ice sheet load (Watts，2001)

冰川均衡调整模型在前期发展过程中，地球模型总是被假定为横向均匀的(Kaufmann and Lambeck, 2000b；Engelhart et al., 2011；Lambeck et al., 2014；Roy and Peltier, 2015)，但地表地质和地震层析成像清楚地表明，地球内部物质的性质不仅是径向变化的，而且是横向变化的(Bunge and Grand，2000)。横向非均质性对冰川均衡调整的观测存在很大影响，但影响的幅度随冰原中心的位置而变化，也取决于使用的冰川均衡调整测量方法的类型(Sabadini et al., 1986；Gasperini and Sabadini, 1989；Giunchi et al., 1997；Kaufmann et al., 1997)。随后，相关学者从地质和地球物理数据(包括地震层析成像)推导出了更真实、具有横向非均质性的三维地球模型，并结合区域冰川模型进行了相关研究(Kaufmann and Wu, 1998，2002; Kaufmann et al., 2005；Wu，2005；Schotman et al., 2008)。Larsen等(2004)使用基于对冰川变化的观测而建立的黏弹性地球模型(由弹性地壳和低黏度上地幔两层组成)来预测地壳抬升速率及总抬升量；研究表明后小冰河期的地壳均衡反弹可解释近250年来阿拉斯加南部的隆起。Li Tanghua等(2018)利用假定的冰川历史和背景黏性模型寻找能够拟合全球相对海平面数据、冰川均衡调整上升速率和重力变化速率的最佳横向非均质黏性模型，结果表明引入一定幅度的横向黏度变化有助于解决一些全球相对海平面数据中不拟合的问题。

目前大部分的研究主要集中在横向非均质性对模拟结果的影响及其敏感性上，只有少数对横向非均质性冰川均衡调整模型的预测结果与实际观测结果之间的差异进行了比较。冰川消融产生的卸载效应会引发下地壳顶面的回弹，破坏原有均衡状态，以至于需要通过地震等构造活动的调节来达到新的稳态(陈浩和李勇， 2009；Hampel et al., 2010)。气候控制的地球表面载荷的变化(冰川消融)可能对单个正断层的滑移历史起到根本性的控制作用(Hetzel and Hampel，2005)。类似问题的研究与现今全球气候变暖的时代背景密切相关，或成为未来均衡理论及模型发展应用的主要方向之一。

4.2 海山洋岛发育过程

海山洋岛在各种不同的构造环境中均有发现，具有特殊意义的是其与离散型板块边界(特别是与洋中脊)以及转换边界的联系。然而绝大多数海山洋岛形成于远离活动板块边界的板块内部。在其形成过程中，由于因洋壳均衡响应而下沉的部分被先填满，因此建造一座海山所需要的物质远多于在海底地面所能看到的。与冰川均衡调整类似，火山作用会产生大范围的沉降区，其两侧是隆起区(Watts，2001)。均衡理论在海山洋岛中的运用主要表现为对其成因及发育过程的研究。

Watts等(1975，1985，1989，1992)、Tenbrink和Watts(1985)及Rees等(1993)以均衡理论为基础，揭示了夏威夷火山群岛的形成演化过程(图10a)。通过先分离出夏威夷岛的载荷，进而计算载荷产生的挠曲，最后估算其对邻近岛屿沉降和隆升的影响，结果表明紧邻岛屿下方的沉降幅度最大，挠曲影响逐渐向西北延伸至莫洛凯岛西海岸。此外，提出了载荷侧翼区挠曲拗陷的递进加载模式及其和超覆、退覆地层模式间的发展关系——后期形成的火山载荷会改变在原有挠曲拗陷中形成的地层模式(剖面底部的超覆和顶部的退覆所支配的反射体模式)；超覆和退覆在挠曲走向和横向剖面上均可观察到，但在前者显示更为清晰，因为这些剖面方向与载荷的迁移方向一致(图10b)。

4.3 山脉隆升与盆地挠曲沉降

造山带在形成后易遭受侵蚀(造山带物质的移除及其在侧翼的沉积)，从而破坏原有均衡状态——被移走物质部分的地壳隆升及被沉积加载部分的下沉(Watts，2001)(图11a)。快速剥蚀(滑坡、崩塌及泥石流等地表过程)所导致的地壳均衡反弹被认为是除断裂活动及地壳缩短等效应外构造隆升的又一地球动力学机制(Molnar and England，1990；王二七等，2006；石许华等，2008；王岩和刘少峰，2013；闫亮等，2019)。弹性板模型己被广泛应用于盆地的挠曲沉降模拟中(Turcotte，1979；Burov and Diament，1992)，其中与造山带相邻的前陆盆地尤为普遍，如阿尔卑斯山中部的前陆盆地(Sinclair et al., 1991)、美国中部塞维尔逆冲带的前陆盆地(Liu Shaofeng et al., 2004)、玻利维亚的安第斯山前陆盆地(Prezzi et al., 2009)及扎格罗斯山西部的前陆盆地(Saura et al., 2015)等。构造和沉积载荷控制了前陆盆地一级构造单元(构造楔、前渊、前隆及隆后)的形成(DeCelles and Giles，1996)，对于前陆盆地弹性挠曲的模拟有助于我们认识盆地的形成和迁移规律，以及造山带剥蚀速率、逆冲速率和岩石圈挠曲刚度与盆地充填的关系。

以塔里木盆地为例(Yang Youqing and Liu Mian，2002)，在印度板块与亚欧板块碰撞的背景下，盆地在新生代因西昆仑山、天山和阿尔金山的隆升而与西部的特提斯洋隔绝，形成封闭的陆相沉积盆地(Sobel et al., 2003；Bosboom et al., 2014)。Li Chao等(2020)采用一端带构造载荷的弹性有限板模型模拟了盆地沉降史，预测的26 Ma以来最优地壳有效弹性厚度(Te)值的增加与盆地冷却史一致；挠曲凸起自26 Ma以来向西昆仑迁移了约52 km，反映了西昆仑山相对于天山所占载荷比例的下降(图11b)。在研究与盆地挠曲沉降相对的山脉隆升方面，阿尔卑斯山地区出露的角闪岩相和高压绿片岩相岩体表明侵蚀作用已从变形的地壳上移走了不少于16 km的覆盖层(England，1981)。Champagnac等(2007)利用地球物理方法和阿尔卑斯山的平均侵蚀速率，分别量化了侵蚀的空间分布范围和被侵蚀岩石的体积，表明至今约50%的垂向运动是由上新世—第四纪期间侵蚀增强后的均衡响应造成的。

图10 夏威夷群岛形成过程及海山对地层发育的影响示意图Fig. 10 The formation process of the Hawaiian islands and the influence of seamounts on stratigraphic development(a) 夏威夷山脊被相继放置在其东南端的年轻载荷逐渐加载；细虚线描绘了夏威夷岛产生的载荷，其导致邻近的毛伊岛和莫洛凯岛下沉及欧湖岛隆起；粗虚线表示不同时代火山脊的沉积边界(Watts and Tenbrink, 1989)。(b) 海山岛链挠曲拗陷的递进加载模式及其与超覆、退覆地层模式的关系(Watts et al., 1989)(a) The Hawaiian Ridge was gradually loaded by younger loads placed in succession at its southeastern end. The thin dashed line depicts the load generated by the Hawaiian Islands which has caused the subsidence of Maui and Molokai, and the uplift of Oahu. The thick dashed lines are the sedimentary boundary of volcanic ridges during different ages (Watts and Tenbrink, 1989). (b) The progressive loading model and its relationship to the stratigraphic patterns of onlap and offlap in the flexural moats of seamount chains (Watts et al., 1989)

均衡理论及模型对研究山脉隆升、盆地挠曲沉降机制与发展演化史和盆山耦合关系起着重要作用。构造变形通过地壳均衡作用影响地表过程及相应的构造应力和构造变形模式的分布。褶皱冲断带(造山带)构造变形与地表过程的相互作用，以及地表侵蚀和(盆地)沉积作用对构造变形空间分布、形态、幅度和过程的影响已有相应的研究(Willett，1999；Beaumont et al., 2001；Mao Yuqiong et al., 2021)。但是，山脉的隆升与盆地挠曲沉降往往是多种因素的综合效应，如何优化约束条件、更好地通过对构造活动、地壳缩短和均衡反弹等效应的剥离计算来定量厘定单一因素的贡献量对深入理解相关地球动力学机制尤为重要。

4.4 变形湖滨线

大型湖泊在其形成期间及形成后产生的强大水文载荷会导致地壳的挠曲变形；变形湖滨线的研究对理解地壳均衡反弹、约束壳幔流变参数、研究构造演化及限定地壳有效弹性厚度(Te)等方面起着重要作用(Crittenden，1963；Passey，1981；Nakiboglu and Lambeck，1982；Bills and May, 1987; Bills et al., 1994a，b)。最早表明地球内部会对其表面载荷的变化做出黏弹性响应的证据来源于对美国西部博纳维尔湖(Lake Bonneville)古滨线变形模式的研究(Gilbert，1885)，由此引发了该领域的研究热潮，相关研究成果丰富。

Cavalie等(2007)定量研究了近10年(1992～2002)米德湖(Lake Mead)附近因水位变化引起的变形，并对湖区的壳幔流变参数进行了约束，表明Kaufmann和Amelung(2000a)提出的双层黏弹性模型(地幔黏度为1018Pa·s)可以很好地拟合现有数据幅度及其时空形状，与Dixon等(2004)估计的美国西部上地幔黏度(1018～1019Pa·s)一致。Govers等(2009)认为墨西拿期(Messinian Age)地中海地区蒸发岩载荷所导致的均衡挠曲及水文载荷消除所引起的均衡回弹影响着周边河流峡谷和地形斜坡的发育，通过对区域均衡构造贡献的研究，提出该地区分别发育有因挠曲作用和干燥作用所产生的两个不同成因的侵蚀面(图12a)。Shi Xuhua等(2015)基于西藏中部色林错湖面历史及伶侗湖滨线的变形特征，采用圆盘形载荷作用下弹性薄球壳拟三维挠曲方程，通过湖滨线高程变化范围和空间分布与均匀弹性板所预测变形的拟合，限定了西藏中部的地壳有效弹性厚度(Te)为20～30 km；在黏弹性松弛对湖退完全性响应的前提下揭示了下地壳的最大平均黏度为(1～2) × 1019Pa·s，与十年时间尺度下从震后松弛估计的黏度相当(图12c， d)。Austermann等(2020)利用更新后的博纳维尔湖和拉洪坦湖(Lake Lahontan)年代学及校正后的湖滨线特征高程数据集，重新研究和扩展了博纳维尔湖这一经典的均衡反弹课题，表明美国西部的洪积湖可以对劳伦太德(Laurentide)冰原及其外围隆起的形状和下部地幔黏度形成有力约束——穹状变形需要一个具有薄地壳有效弹性厚度(Te)(15～25 km)和低黏度(1019Pa·s)的区域性地球结构。与利用冰前的湖泊来限制冰原演化和地幔黏度(Gowan et al., 2016；Lambeck et al., 2017)不同，Austermann等(2020)首次研究了导致远距离洪积湖滨线变形的因素(图12b)，支持了“地球内部性质的横向变化在全球海平面研究中有着重大意义”的观点(Li Tanghua et al., 2018)。

图11 山脉隆升与盆地挠曲沉降示意图Fig. 11 The diagram of the uplift of mountain and the subsidence of basin(a) 山体遭侵蚀引起的均衡调整。侵蚀使地壳厚度减薄，因此地表相对于大地水准面下移；公式为利用Airy模型计算被移除的物质的量(Se)(Watts, 2001)。(b) 塔里木盆地新生代挠曲沉降与总沉积厚度演化示意图(Li Chao et al., 2020)(a) The isostatic adjustments followed by the erosion of a mountain belt, which reduces the thickness of the crust and the downward-moving of the surface with respect to the geoid. The formulas are to calculate the total amount of material (Se) that is removed using the model of Airy (Watts，2001). (b) Sketch of the evolution of the flexural subsidence and the sediment drape in the Cenozoic Tarim Basin (Li Chao et al., 2020)

图12 变形湖滨线研究示意图Fig. 12 The diagram of the study of shoreline flexure(a) 地中海地区两个不同来源侵蚀面示意图，下层蒸发岩的沉积(LM)引起边缘抬升和侵蚀，形成质量流沉积(LC)；干燥产生上层蒸发岩(UM)，同时暴露边缘遭受侵蚀，导致侵蚀/质量流单元(UC)；PQ为上新世—第四纪沉积物(Govers et al., 2009)。(b) 劳伦太德冰原对美国西部古湖泊影响的示意图，预测位于外围凸起远端的古滨线会向冰原方向下斜，这是固体地球变形和劳伦太德冰原不断变化的引力共同作用的结果(Austermann et al., 2020)。(c) 正演弹性模型预测地壳变形模式，白线为计算变形量，带颜色圆圈表示预测值和观测值之间的不匹配；(d) 湖滨线高程与预测变形的比较(Shi Xuhua et al., 2015)(a) The diagram of two erosion surfaces of different origins in the Mediterranean. Deposition of the Lower Evaporites (LM) causes marginal uplift and erosion, leading to mass flow deposits LC. Desiccation produces the Upper Evaporites (UM), and simultaneously exposes the margin to erosion, resulting in erosion/mass flow unit UC. PQ stands for the sediments during Pliocene—Quaternary (Govers et al., 2009). (b) The schematic of the effect of the Laurentide ice sheet on paleolakes in the western United States. Paleoshorelines of lakes on the distal side of the peripheral bulge may dip down towards the ice sheet, which is caused by the combined effects of solid Earth deformation and a changing gravitational pull of the Laurentide ice sheet (Austermann et al., 2020). (c) The predicted crustal deflection pattern by forward elastic modeling. The white lines are the contours of calculated deflection, and color-coded circles show the misfit between predicted deflections and observed deflections; (d) The comparison of shoreline elevation versus predicted deflections (Shi Xuhua et al., 2015)

4.5 河流三角洲发育特征

河流三角洲形成过程中沉积物载荷的逐渐增加会导致其下地壳的沉降及侧翼地区的隆升，这种垂向运动对三角洲的发育有着深远的影响。在向海一侧，隆升减少了沉积空间及沉积作用发生的可能性，限制了三角洲的横向延伸；在向陆一侧，隆升增加了源区的高度，从而增加了物源的供应，有利于三角洲的发育(Watts，2001)。

图13 由进积型沉积载荷引起的岩石圈渐进挠曲模型(Watts, 1989)Fig. 13 The schematic model for the progressive flexure of the lithosphere due to a prograding sediment load (Watts, 1989)剖面从上到下分别显示初始载荷及其产生的挠曲、添加第二次以及最后一次载荷的效果The profile from top to bottom shows the initial load and resulting flexure, the effect of adding a second load and the final load respectively

虽然早期的地壳均衡论者认识到了河流三角洲这一地质体的重要性，但他们不认为挠曲作用会对其发育产生影响(Barrell，1914；Lawson，1942)，直到Walcott(1972)在几十年后才重新认识到了这一点。进积型河流三角洲体系中不同的几何剖面形态取决于它们是由河流体系过程主导还是由沉积盆地作用主导。Watts(1989)假设岩石圈为一个弹性薄板，覆盖在非黏性流体之上，提出了由进积型沉积载荷引起的岩石圈渐进挠曲模型(图13)。该模型可以通过追踪两个坡折(一个位于陆架和斜坡之间，另一个位于斜坡和盆底之间)来预测最终沉积楔中相的分布特征。Zhang Huiping等(2014)用二维应变模型量化了因侵蚀卸载而引起的均衡响应，在古青海湖更新世溢洪道附近，利用不同地壳有效弹性厚度(Te)计算得到了最大垂向位移变化范围为160～260 m，表明在0.5～1.2 Ma内，黄河流域因河流下切引起的均衡响应破坏了局部支流，使青海湖孤立，形成内流河盆地。

目前对于挠曲均衡影响河流三角洲发育过程的研究相对较少，多关注于三角洲的沉积相特征、煤系烃源岩分布范围及油气成藏潜力等社会经济问题。

4.6 水库变形

由地壳均衡理论可知，大型水库在其运营过程中，因水位升降引起的水文载荷变化会导致岩石圈的挠曲变形。大幅度的变形严重影响着水库大坝及库区建筑设施的安全，甚至诱发地震等地质灾害(Ge Shemin et al., 2009；Kerr and Stone，2009；Paronuzzi et al., 2013；Gahalaut et al., 2018)。目前对于水库蓄水后产生变形的研究多局限于浅表(Li Mingwei et al., 2020)，尚未考虑到蓄水对地壳深部的影响，对最大变形量缺乏科学预测，相关问题需引起安全生产部门的高度重视。

Madson和Sheng Yongwei(2020)采用球对称、非旋转、弹性和各向同性(SNREI)地球模型模拟了埃塞俄比亚复兴水库在不同的蓄水和操作方案下产生的弹性变形。变形量取决于输入的自然水文变量和操作变量(由水资源管理者决定)。水库蓄水和排水的时间及速度影响着地表水文载荷的强度，进而影响着总弹性变形量和从载荷中心向外延伸的变形范围。研究结果表明无论蓄水周期长短，完全蓄水时产生的最大垂向和水平变形量分别为11.99 cm和1.99 cm。Fu Guangyu等(2021)通过调查获得的自由空气异常和布格重力异常数据，反演了岩石圈密度结构，计算了金沙江白鹤滩水电站库区岩石圈所承载的均衡附加力(均衡面与Moho面之间物质所受的浮力)。在研究了因蓄水引起的重力变化和库仑应力变化的基础上，从岩石圈均衡的角度提出了评估水库诱发地震的新方法，认为在白鹤滩大坝上游约20 km处存在-30 MPa的均衡附加力，该地区发生水库诱发地震的风险值得关注。

相关理论模型和成果经验可用于研究我国大型水电站(如三峡水电站、白鹤滩水电站及溪洛渡水电站等)蓄水后产生的变形及其与地质灾害(滑坡、崩塌、泥石流及水库诱发地震等)的关系，为后续库区地质灾害防治、地质环境保护及新建水电站的选址等工作提供科学依据。

4.7 同震滑坡

大型地震是触发山体滑坡的主要因素，会造成显著但空间上不均一的侵蚀(Keefer，1994；Malamud et al., 2004；Larsen et al., 2010)；山体滑坡在驱动山地演化的构造和地表过程间的竞争中起着主导作用(Hovius et al., 2000；Whipple，2009)。因此，大型地震在产生同震岩体隆升和促进滑坡侵蚀中的相对作用对于理解地壳平流和剥蚀之间的平衡至关重要。震级、同震滑坡的分布和岩体隆升三者之间的相互作用引发了大型地震及同震滑坡是否会改变山区地形的问题(Parker et al., 2011)。相关问题的研究在2008年Mw7.9汶川地震后取得可观进展，逐渐由定性分析转向以地壳均衡为基础的定量讨论(Parker et al., 2011；Ren Zhikun et al., 2017，2018；Lei Jinghao et al., 2021)。

Parker等(2011)利用高分辨率卫星图像上滑坡的面积—体积比例关系来研究造山带体积的潜在变化；通过其估计的同震滑坡产生的可蚀物质量(5～15 km3)与因同震岩体隆升向造山带提供的净物质量(2.6±1.2 km3)之间的差异，表明即使在地震间隔期内只有一小部分滑坡物质从造山带被移走，汶川地震也会导致龙门山地区物质的净亏损；该结论挑战了大型倾滑或斜滑地震产生山地地形的观点，并建议更仔细地考虑同震滑移、物质坡移和地形生成之间的关系。Ren Zhikun等(2017)定量区分了地震侵蚀在总侵蚀中的影响(地震侵蚀率占总侵蚀率的50%)，认为地震侵蚀在构造地貌研究中发挥着重要作用(尤其是在造山带)；利用重新估算的同震滑坡体积，量化了滑坡体移除后的均衡响应(平均均衡回弹0.9～0.24 m)，表明龙门山地区局部地形的演化与反复发生的构造事件有关。在长期的地貌演化过程中，地壳均衡对隆升的作用不可忽视(Ren Zhikun et al., 2018)。Lei Jinghao等(2021)对2004年日本中越地震的研究结果表明，地震增大了中越低海拔地区的地势差；现存地形不仅受到断层相关褶皱作用所导致的隆起的影响，也受到地震滑坡的侵蚀及地壳反弹长期的调整；剥蚀深度、预测的均衡回弹以及褶皱变形分布三者与地形剖面表现出不同的模式。这种不同于在古老而陡峭的龙门山造山带观察到的变形模式表明强震可能会在平缓和陡峭山区的地质、地形演化中发挥不同的作用。

滑坡碎屑沉积物的重新分配以及震间垂直运动影响着同震滑坡产生的挠曲均衡响应常在实际研究中被忽略。虽然岩石圈有限挠曲刚度不会改变均衡补偿向上运动的量，但它可能会把向上的位移扩展到比滑坡位移更大的区域。进出造山带的物质通量对了解在特定时间尺度上的真正体积平衡有着重要意义。均衡响应的时间尺度在一定程度上影响着地貌演化的进程(王伟等，2018)。这些问题都是在未来同震滑坡的研究中需要加以考虑的。

5 讨论与展望

地壳均衡理论和相关模型自产生、发展及趋于成熟经历了漫长的时间，不同均衡模型各有其限定条件及优缺点。我们在运用其研究解决实际地质问题时需从多方面进行综合考量。目前大多数均衡模型主要用于定性研究地质体特征及其形成过程。世界范围内大型冰川的消融(Wang Puyu et al., 2017；Liu Juan et al., 2020)、大型水电站的运营(Tang Huiming et al., 2019；Tang Minggao et al., 2019；Li Mingwei et al., 2020)及大型地震等引起的地壳挠曲变形缺乏长期的、大范围的实时监测。均衡响应引起的浅表高落差地区地质灾害(崩塌、高边坡失稳及滑坡等)的防治及地质环境的保护等问题需引起重视并有待深入研究。

近些年来，已有学者将不同的均衡模型及计算方法进行整合优化(Wickert，2016；孙少波等，2018；范雕等，2019；Hampel et al., 2019；张星宇等，2020)，使其更加适用于普遍情况。但研究力度及成果有待进一步加强提升，特别是应重点考虑把弹性情况下的经典模型改善后运用于黏弹性条件中，或优化黏弹性条件下的均衡模型及计算方法，重点考虑实际地质体不均匀的一般情况，使模拟结果更接近现实情况。另一方面，均衡模型从理论上对其在不同领域中的应用及时空边界进行了限制，模型的空间边界包括造山带、盆地及断裂等；而模型的时间边界在实际研究中往往模糊甚至被弱化。在运用不同模型研究不同时空尺度地质体特征时，相关模型的适用条件也需予以重点考虑。

在未来的研究中，可以结合高精度遥感与大地观测技术——特别是全球定位系统(GPS)与InSAR(合成孔径干涉雷达)测量技术，深部结构研究方法——地震学与地球物理学，以及地质年代学方法——尤其是多系统低温热年代学定年(磷灰石、锆石裂变径迹与(U—Th)/He)、光释光(OSL)测年、高精度AMS14C与U系测年以及原地宇宙成因核素定年(TCN)等，有效地提升对各类地质体特征定量研究的精度。在此基础上，进一步解决“全球地幔动力学与地表地形”、“利用地表抬升和沉降的地质记录限定构造地貌过程”、“气候、侵蚀和构造之间的相互反馈作用”(李广伟，2021)以及“地壳均衡—地表过程—构造活动—气候变化耦合关系”等构造地貌研究中的关键问题。地壳均衡提供了将地球深部活动与地表过程进行结合的新视角，一定程度上补充了传统研究体系的不足。因此，充分思考地壳均衡理论在研究“深—浅耦合”这一科学问题中扮演的角色，对全面、系统地了解地表过程、地球深部过程与动力学和地球圈层之间的相互作用具有重要指导意义。