既有铁路车站线位拟合与成图研究
2022-08-02王庆辉
王庆辉
(中铁第五勘察设计院集团有限公司郑州院 河南郑州 450000)
1 研究背景
既有铁路车站改扩建,需要获取合理的既有线线位作为基准进行工程设计[1-2]。在铁路车站的勘测实践中,既有铁路车站各股道的测点均以散点形式提交成果,为离散点,各股道的离散点连线后为0阶连续折线,不可为设计直接使用,具体设计过程中,需将各股道按“直线+曲线”进行处理。
车站为股道群,具有站线股道多、组成要素间的几何控制条件多、咽喉区连接情况复杂等一系列特点,测量数据拟合的研究资料较少[3]。现状车站线位拟合主要是通过设计人员根据测量数据手动调整定位,将各股道离散的测点数据,拟合还原为(直线-曲线-直线)的连接形式,通过目测和手动量距离的方式,使测点较为均衡地分布在拟合后股道的两侧,拟合成果质量好坏与设计人员的经验直接相关,拟合效果不能直观评价,拟合质量难以得到保证,且效率较低,不符合当下信息化、智能化设计的要求。
本文主要对多股道车站线位拟合进行研究,将工作实践中的基于手动和经验的数据处理方式,转变为基于数理统计方法的智能数据处理方式,并实现计算结果的CAD图形交互式绘制,使车站线路整体拟合效果更优。
2 车站线位拟合的关键问题及处理研究
铁路车站由正线股道、站线股道、咽喉区道岔、岔后直、曲线组合而成,为实现车站的整体拟合,将车站按组成结构进行分解,对各组成部分进行分步拟合。车站各组成部分在平面空间存在确定的“几何-约束”关系,车站正线与区间正线贯通,车站各站线股道由正线设道岔依次、发散引出,引出站线股道的道岔区即为车站的咽喉区,由诸多道岔、岔后直、曲线组合而成,车站咽喉区引出站线股道的组成结构分析示意图见图1。
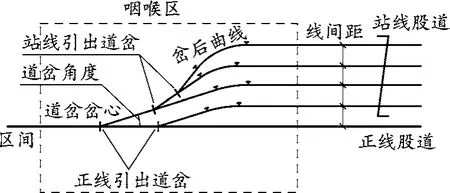
图1 车站咽喉区引出站线股道的组成结构分析示意
2.1 基准线及其计算模型选择
车站由诸多股道和咽喉区组合而成,各组成部分之间存在联动关系,车站的整体拟合,首先应确定车站线位拟合的基准线,达到定一线基准而定整体的目的。车站正线与区间正线贯通,为站内运行速度最高的股道,养护条件要求高,要求线路平顺性指标最为严格,采用站内正线为车站线路整体拟合的基准线可行性更高。在勘察设计实践中,传统手动方式处理车站线位拟合,也是先定正线,选择正线为车站线路整体拟合的基准线。由上分析,本文车站线位拟合应选用正线为基准线。因车站其他部分均由正线发散引出,车站正线为车站的骨干,正线拟合的精度直接决定车站线路整体拟合的质量,所以正线的拟合为车站线路整体拟合的首要关键问题,应选用更为精确的计算模型。
在拟合计算过程中,往往将线路分为直线与圆曲线两个部分[4]:对于铁路直线地段,可以由直线段落上的测量数据的其中两个数据求出该直线方程;在圆曲线地段,可由三点确定圆曲线半径及圆心坐标。但是既有线路往往运行多年,在列车的重复荷载下线路大多难以保持原有的形位,单凭既有铁路直线段上的两点或圆曲线上三点,用于反映直线段或曲线段的线形会引起较大的误差。为保证既有线拟合的精度,本文使用最小二乘法结合坐标法对观测数据进行整理。最小二乘法的原理是利用全部测点的数据进行线形的确定,求出直线或圆曲线方程,使得测点数据与拟合方程间误差的平方和为最小,减少由于线路变形、测量误差给线形确定带来的不良影响,可以有效提高既有车站线位拟合的精度。
常用的普通最小二乘法仅考虑了因变量y存在误差的情况,它通过最小偏差的平方和,寻找适合观测数据的最佳匹配函数。以直线为例,其数学原理为:给定一组数据(xi,yi),(i=1,2,…,n),寻找由a、b参数,构成的最佳理论模型函数y=f(xi;a,b),(i=1,2,…,n),使残差平方和最小,如式(1)。

从几何意义上讲,就是寻求与给定点序列(xi,yi),(i=1,2,…,n)的纵向距离平方和为最小的曲线y=f(x)。而在铁路勘察实际的测点测设工作中,x、y两个方向为等精度,两个方向的偏差均存在,如采用普通最小二乘法,会使拟合精度降低。正交方法能够同时考虑自变量x和因变量y的误差,对于直线、曲线拟合,为更好地反映测量实际,本文采用基于正交距离最短的最小二乘法计算模型作为直线、曲线拟合的方法[5]19-21。普通最小二乘法和正交最小二乘法的误差对比[6-8]见图2。
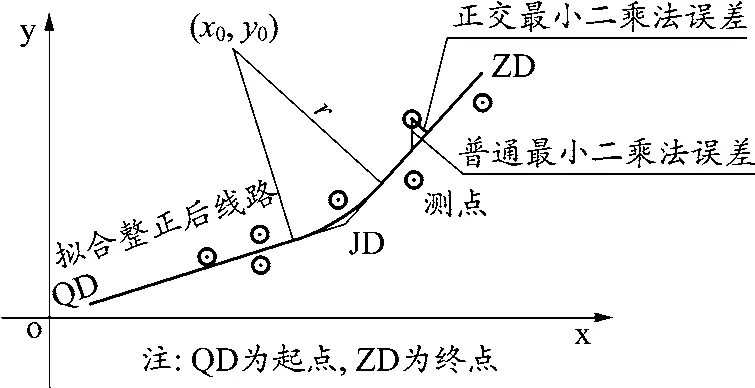
图2 普通最小二乘法与正交最小二乘法误差对比示意
2.2 站线股道的定位
站线股道由咽喉道岔引出,具有与正线平行的约束关系,站线股道定位的关键问题是与基准线的间距确定。通过计算站线各测点至基准线距离,以相邻测点距离基准线的差值≤0.12 m为阈值,对测点进行分组,对落到同一分组范围内的测点,计算到基准线距离平均值作为待求股道到基准线的线间距,绘制股道平行线,完成平行股道的拟合,实现站线定位[9-12]。程序编写流程见图3。
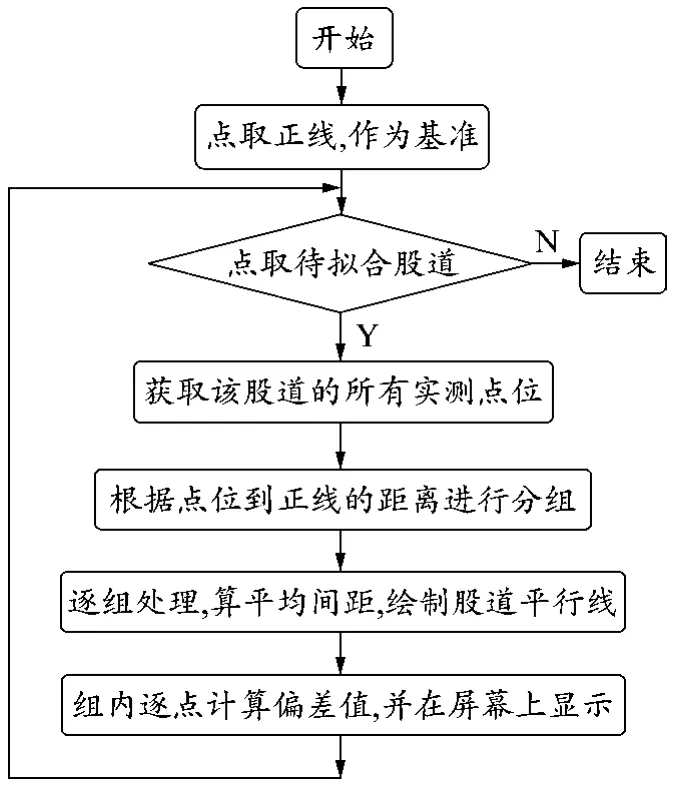
图3 平行股道定位流程
2.3 咽喉道岔的定位和岔后曲线的连接
咽喉区由诸多道岔、岔后直、曲线组合而成,需理清各组成部分之间的连接关系,按照道岔引出的次序,“先正线,后站线”依次拟合,咽喉拟合的关键问题是确定岔心坐标和岔后曲线半径。可通过前后移动岔心在其落位股道上的投影坐标方式,以道岔直股方向和道岔角度为固定值,以道岔岔心测点投影坐标和岔后曲线半径为变量,计算岔后直、曲线段落内测点偏差值,以偏差值之和最小为优化目标,实现道岔岔心坐标和岔后曲线半径的确定[13]。对于两正线间渡线,考虑两组道岔间的联动关系,分别求渡线两端道岔投影坐标,并以此求解另一端道岔岔位与实测点偏差值的计算方法,对于2种计算结果,选择偏差值小者为渡线位置。咽喉区拟合采用的相关的计算公式推导如下。
假设A(x1,y1)点为测点坐标,所在股道的直线方程为y=kx+b,a′(x0,y0)点为A点在落位股道上的投影坐标,如图4,根据a′(x0,y0)在直线y=kx+b上,则有a′(x0,kx0+b)。
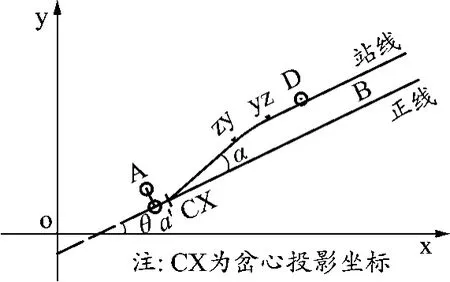
图4 岔后曲线连接示意
Aa′与直线y=kx+b垂直,则有:
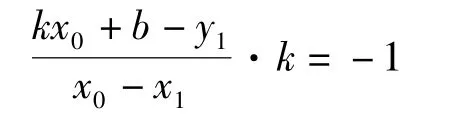
解得测点投影坐标如式(2)。

由上,如测点为岔心,可确定岔心的投影坐标。
2.4 偏差值的计算
通过求点到拟合线路的距离,可得到测点至拟合后线路的偏差情况,验证拟合效果。直线、圆曲线段落范围内的点,点到拟合后股道的距离可通过几何关系直接求得;铁路缓和曲线的线形为三次抛物线,点到缓和曲线距离按迭代法进行计算[5]62,参数方程较为复杂,详见相关参考文献。
直线地段测点到拟合直线方程的垂直距离,可用式(3)表示:

式中,k、b分别为直线方程的截距和斜率;xi、yi为直线段落测点坐标。
圆曲线地段按测点到圆心距离与半径差值,可用式(4)表示:
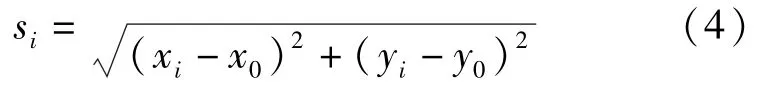
式中,(x0,y0)为圆心坐标;R0为圆心半径;(xi,yi)为圆曲线段落测点坐标。
3 成图研究
既有铁路车站线路整体拟合的实现过程,按照数据准备,数据展点,正线线位拟合,平行股道线位拟合,道岔及岔后曲线线位拟合的顺序,完成了测点数据的计算及整正结果的CAD交互式成图。具体为:根据前述车站整正流程及计算理论方法,使用python语言,编写了正交最小二乘法的直线和圆曲线参数计算的通用函数,实现了正线参数的计算;基于CAD平台,采用lisp二次开发语言,编制了计算机辅助工具插件,完成了在CAD端数据的自动化读取、成果的导入和计算、偏差值的校验,并可根据测点计算情况对结果进行成图绘制与输出,实现了测点计算-绘制-出图的一体化。
4 算例
既有陇海铁路观音堂车站为双线铁路车站,车站性质为中间站,站内正线2条,站线6条,有单开道岔、交叉渡线、交分道岔,道岔型号有12号道岔及9号道岔,设有两正线间渡线,车站具有较强的代表性。以陇海铁路观音堂车站为例[14],以各股道测设数据为基础,对数据进行拟合整正分析,并按示意图5所呈现的车站平面关系,完成车站平面图的交互式绘制工作。

图5 既有陇海铁路观音堂车站平面布置
案例实操中,第一步,对正线测量数据按直线、缓和曲线、圆曲线属性不同,进行测点分组,整理数据格式,代入不同的计算模型进行拟合计算,实现正线的拟合;第二步,站内其他股道基于与正线平行,计算线间距,从而实现站内其他股道的定位;第三步,整理全站道岔表,实现道岔在所在股道上的落位,并按岔后曲线半径连通其衔接股道,从而实现全站的股道拟合整正,完成车站的还原。利用本文方法,在测量过程中,可实时进行车站测量数据的拟合计算,通过拟合成果与测设数据的比对,计算偏差值情况,对于偏差值较大的情况,可及时反馈至测量,及时核对测量成果。通过陇海铁路观音堂站拟合整案例,得出以下结论。
(1)直线段股道长度越短,拟合效果越好,以正线Ⅰ股为例,线段长度小于500 m的两段,拟合最大偏差值为0.02 m,线段长度大于1 000 m的一段,拟合偏差值95%落在拟合控制精度指标0.045 m范围,最大偏差值为0.075 m,对于异常点需实时反馈至测量校核,确认测量无误后,需将其整正调整至拟合股道位置,既有线养维或改建设计时,可由此计列相关的整道拨距工程数量。
(2)交叉渡线上的11、15号道岔错位2.92 m,误差较大,通过数据的快速处理、成图,可及时反馈至测量单位进行核改;8道东段8k0+300~8k0450测点距离基准线差值大于0.3 m,误差过大,需及时反馈至测量单位核改。
5 结束语
车站正线为车站的骨干线,本文采用正线为车站线路整体拟合的基准,将车站进行分解,依次计算,实现正线线位拟合,站线定位和咽喉区拟合,然后再组合成车站整体,“分解-组合”的方法是可行的。
本文研究结果应用于工程实践,具有解决现实问题的实际意义。以陇海铁路观音堂车站为算例,结果表明,本文所提出的方法能快速完成车站线位拟合,工作效率有倍级以上的提高,为车站线位拟合的计算分析提供了一定的理论方法。
