超大跨度竖索体系线弹性分析验证及应用

王 屹，李 健，刘传传

(1.北京江河幕墙系统工程有限公司，北京 101399； 2.四川合奇美建筑装饰工程有限公司，四川 成都 610096； 3.上海江河幕墙系统工程有限公司，上海 201601)

0 引言

带有多排开启窗的索网幕墙，是一种具有新功能、新外观形式的索网幕墙。为了保证固定在索网上的开启窗能正常开启，要求索网竖索体系中开启窗位置的控制精度必须在2mm以内，精度要求高，控制难度大。

上海证券交易所主楼(60.100～175.515m)拉索幕墙净空高度115m、净宽度24m。单幅索幕墙面积2 760m2。在结构标高168.250～175.515，85.025～90.465m 位置分别设置6排，共计12排168个开窗，如图1，2所示。

图1 带有开启窗的索网幕墙

图2 带有开启窗的索网幕墙开启窗待安装状态

由于竖索体系中的各点在竖索张拉和面材安装过程中索体受力发生变形，因此存在索力和设定位置的协调动态变化，为了确保开启窗的设定位置能按设定值准确被安装，系统设计阶段考虑将开窗竖向外框设计成钢板形式，将钢板作为竖索体系的一部分，参与索网结构体系的变形和受力，如图3所示，这样的竖索结构体系设计既能保证整片索网幕墙固定的整体性，又同时兼顾满足开启窗外框刚度的安装和使用条件。使得开启窗特殊点位的精确定位控制成为可能。

图3 竖索体系结构示意

为了简化施工操作，快速实现复杂受力状态下的现场调节，张拉端设在竖索体系的底部调节端。施工流程为：在一个较小张力状态下，保持竖索的垂直度和张紧状态，然后通过目标应力与提前施加的较小张力差值计算出变形差值，进而通过测量数据综合计算出调节量，在中部调节端和底部调节端按上述计算值反向调节完成后，在底部调节端一次张拉。当预张力变化在偏差范围内，中部和底部的调节端调节至设计理论标高，即完成竖索体系的张拉和调整，操作流程为：对挂好的竖索施加一个较小预拉力，本例按50kN→得出与目标张力的差值后，计算调节部位变形值→根据计算出的变形值对调节端进行反向调节→在底部张拉端张拉→施加并观测索力达到偏差范围内，微调调节端至设计理论位置，完成张拉调节工作。

1 竖索体系受力变形分析

1.1 竖索体系弹性变形解析

由于串联了钢板，使得竖索体系不再是单一的索体结构，同时，竖索体系在受力状态下发生变形，这使得在设定张力的状态下找寻固定开启窗的钢板的准确位置更加复杂。

由多个弹性体串联的竖索体系长度为：

L=L1+L2+L3+…

竖索体系变形用胡克定律表达：

第1段弹性体的弹性变形值为：

第1段加第2段弹性体的弹性变形值为：

第1～3段弹性体的弹性变形值之和：

竖索体系总的弹性变形值为：

由公式推导的过程可知，由若干个弹性体串联成的竖索体系仍满足胡克定律。

为了能在施工现场快速计算和调节索结构，需推导出以索体为基准参照的一个简化公式，使用占整个竖索体系长度90%的索材料的截面积代替竖索体系截面积，利用已知的竖索体系的总长、所受拉力计算出竖索体系任意位置的变形值。

1.2 竖索体系平均弹性模量的分析与计算公式推导

考虑分析和推导是基于胡克定律进行，因此索网体系的张力和面材荷载都在材料的弹性范围内。

推导过程如下。

各弹性体与基准弹性体截面积比为：

各弹性体与基准弹性体弹性模量比为：

各弹性体与基准弹性体长度比为：

当将竖索体系总的弹性变形值公式中的Sn换成占比较大的索体截面的αn·S1形式时，公式可以转换为：

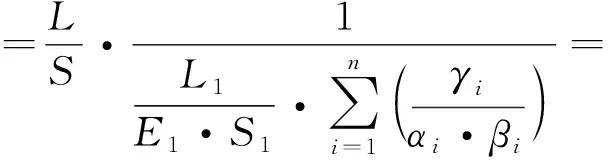
经推导，竖索体系的综合弹性模量：

式中：E1为竖索体系中索的弹性模量。

如图4所示，竖索体系组成结构为：7 625mm长钢板+77 785mm长索+5 440mm长钢板+24 925mm长索。其中，钢板总长Δ=Δ1+Δ2=12 705mm，索体总长L=L1+L2=102 710mm。

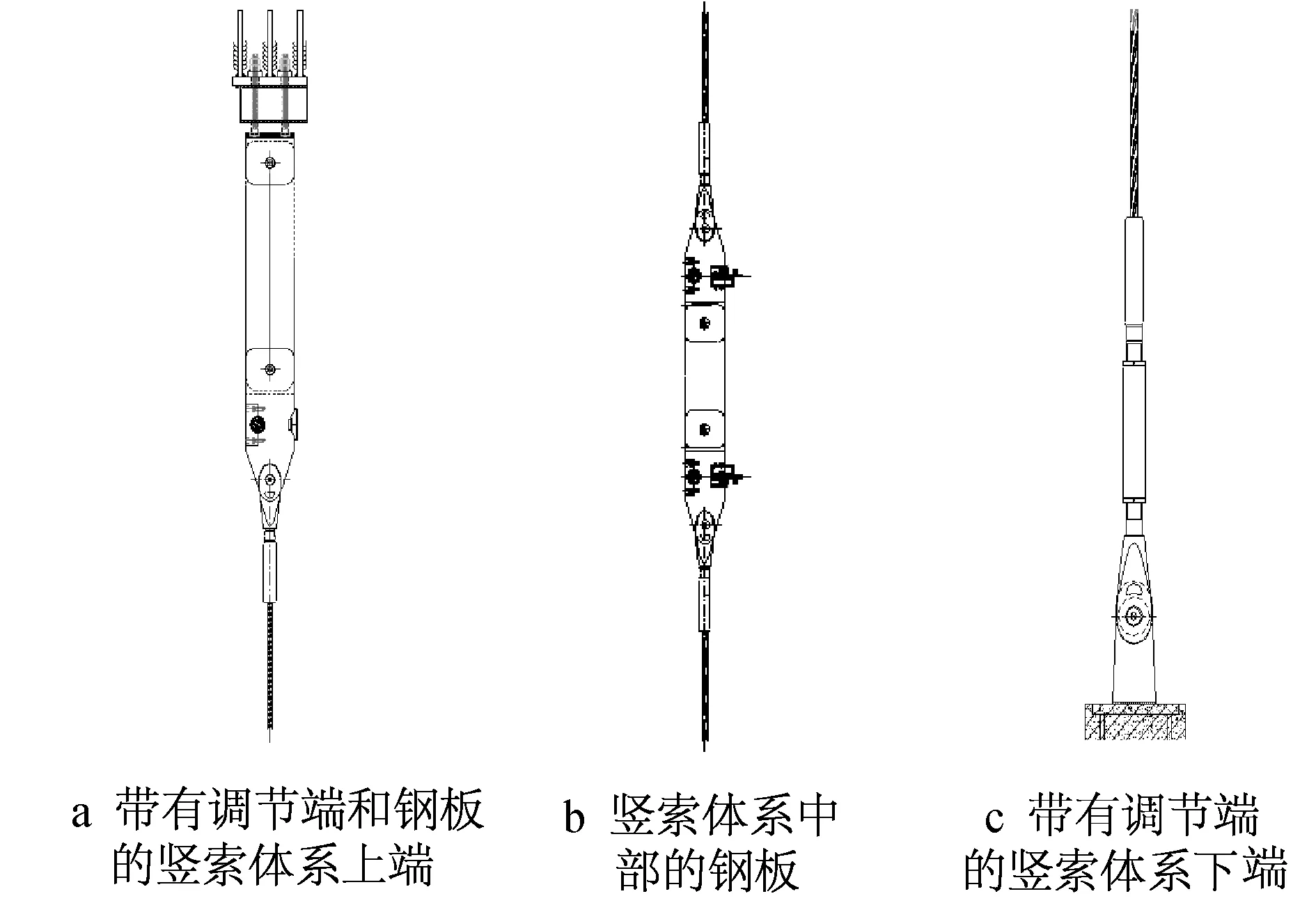
图4 竖索体系调节端示意

钢板横截面积SΔ=190×20=3 800mm2，钢的弹性模量E=2.06×105N/mm2。

拉索直径28mm，有效截面积463mm2，厂家给出的索的弹性模量E1=1.6×105N/mm2。

按照上述推导公式，应用索生产厂家提供的参数E1=1.6×105N/mm2，当取不同长度的竖索作为参考基准计算时，两种情况下，计算得到的竖索体系的弹性模量计算结果一致，E=177 711N/mm2，如表1，2所示。

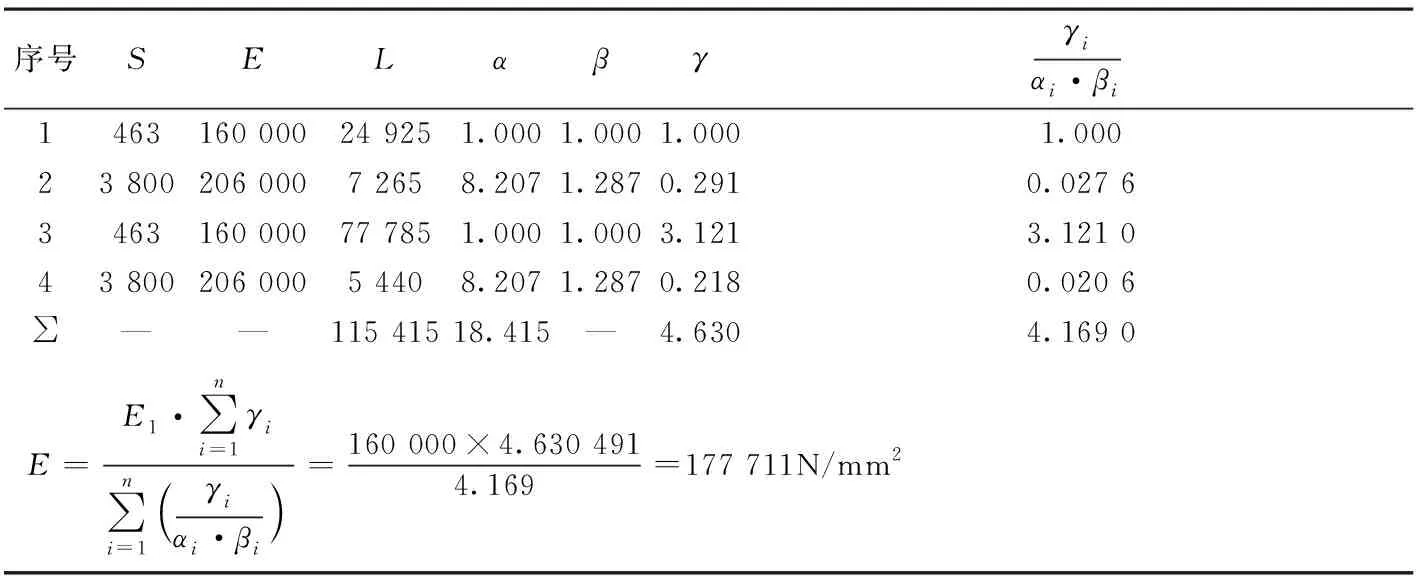
表1 以77 785mm长索体为基准计算的各项系数与竖索体系的综合弹性模量

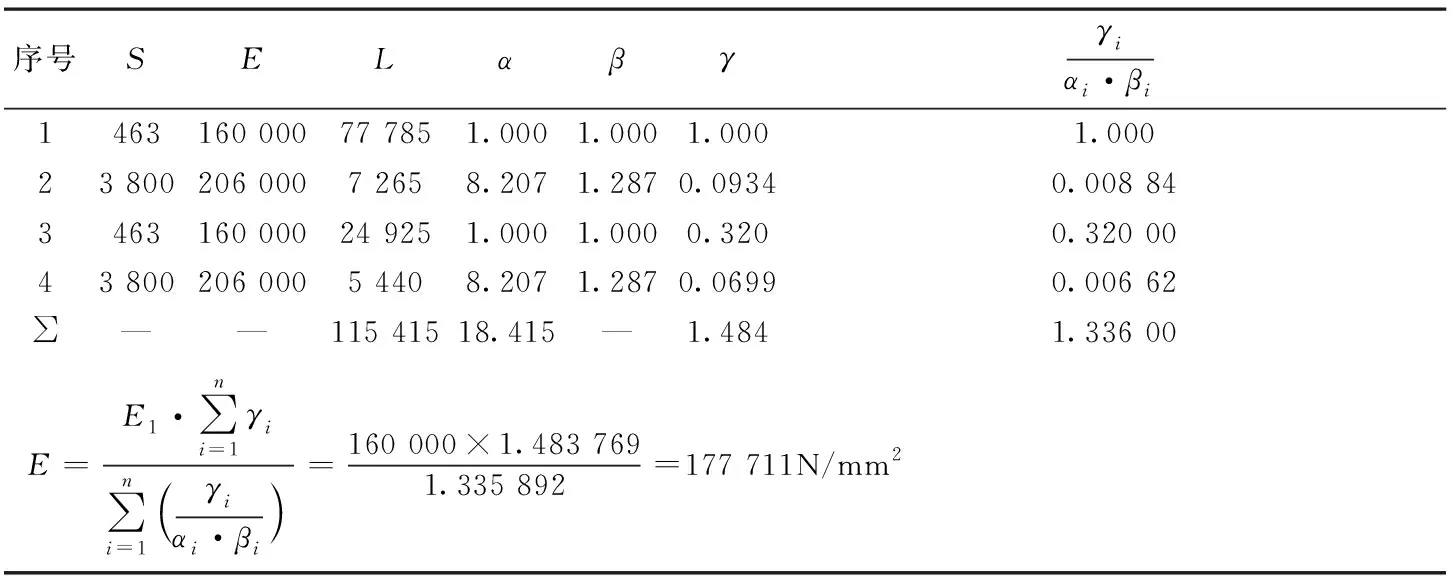
表2 以24 925mm长索体为基准计算的各项系数和竖索体系的综合弹性模量

2 张拉过程中发现的问题

在竖索体系张拉过程中发现，按厂家提供的索体弹性模量为1.6×105N/mm2在应用到变形公式计算预调节值的过程中发现，当所有竖索体系在预张力已达到设计要求时，中部调节端的位置全部比理论标高的数值低4～5mm。

从数值偏差规律可估算出实际竖索体系的弹性模量比1.6×105N/mm2略小，由于偏差达到4mm，已经超出偏差可接受范围，经分析，现场使用的测量设备精度可控制在1mm以内，可排除测量误差较大的顾虑，考虑到索体结构和加工工艺对索体的线弹性模量产生的影响，索的实际线弹性模量与理论数值可能存在偏差。结合JGJ 257—2012《索结构技术规程》中第4.2.5条“索体材料的弹性模量宜由试验确定”条文意见，在现场对竖索的线弹性特征进行验证。

3 索体的线弹性验证和施工检验

验证过程是对15根长度为77 785mm的竖索和15根长度为24 925mm的竖索分别进行张拉和测量，在此只列举长度较大的77 785mm的索的线弹性分析。由于竖索的长度较大，卷盘运输的竖索不能达到伸直状态，弯曲的竖索具有一定刚度，所以需要施加较小的预拉力F0作为竖索的初始拉力，在此拉力下，竖索可有较小变形和理想的垂直度。根据胡克定律：

第1次张拉力与初始拉力差值变形量计算公式为：

第2次与第1次张拉力差值变形量计算公式为：

对索体进行3次受力张拉和变形监测后，应用上述公式求出每根索的2次拉力差值状态下的弹性模量，取平均后作为索的计算弹性模量E1=153 076N/mm2。

实测数值与厂家给定的E=1.6×105N/mm2相比偏差在(160 000-153 076)/160 000=4.3%。同时，根据索的泊松比、实测的线应变计算出的横向线应变接近0；实测受拉后索体的直径变化接近0，可判断，在本例的拉力下，索的直径变化很小，对索的弹性模量数值影响可忽略，如表3所示。

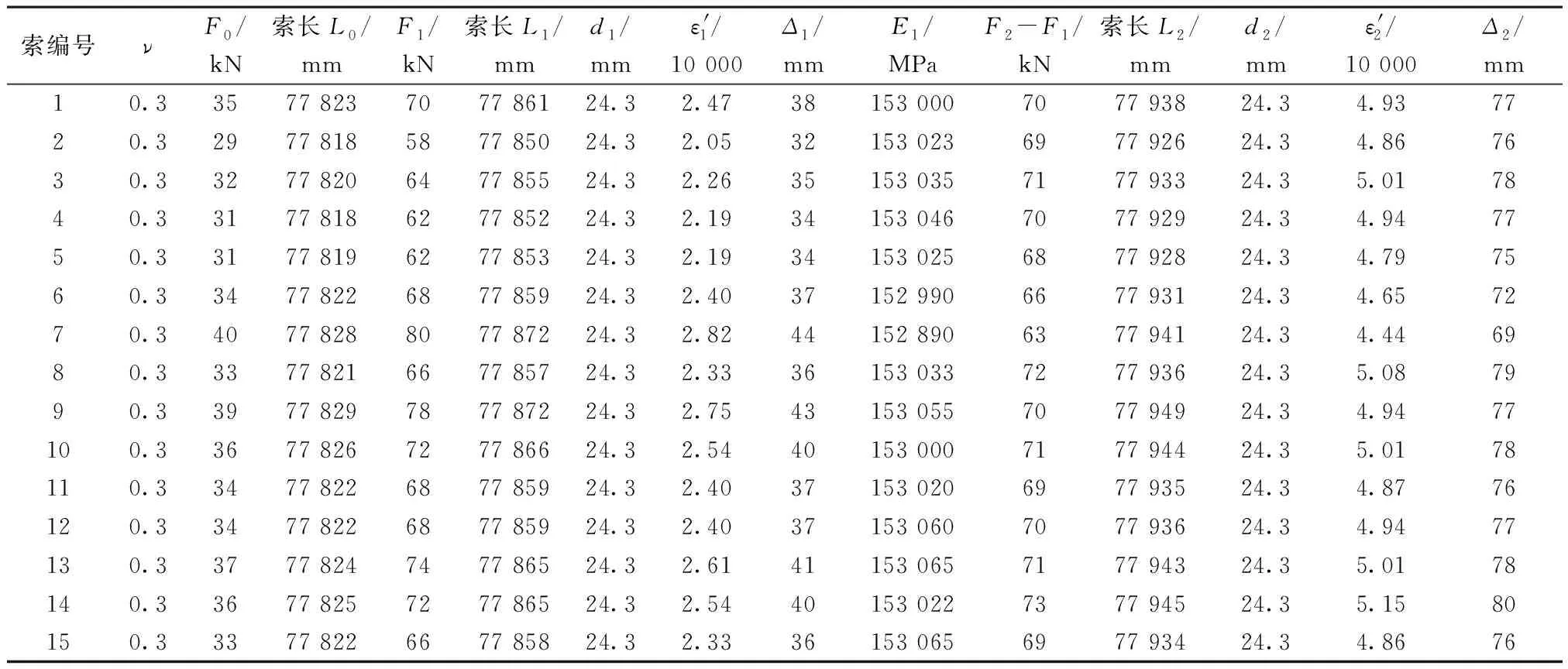
表3 索体线弹性分析张拉及变形测量

通过在张拉过程中实测索的拉力和变形值，应用胡克定律公式计算得出索的实际弹性模量后，按前面推导的计算竖索体系的综合弹性模量的公式，在计算中部调节端位置的竖索体系的弹性模量时，可看出：由厂家给出的索体的理论弹性模量和实测的弹性模量分别计算得到的竖索体系的弹性模量数值有差异，如表4，5所示。这也解释了按厂家给定的弹性模量计算得出的预调节值与实际需要的调节值间存在差异的现象。因此，对于需要精确定位的较长的竖索在现场进行索的线弹性验证很有必要。

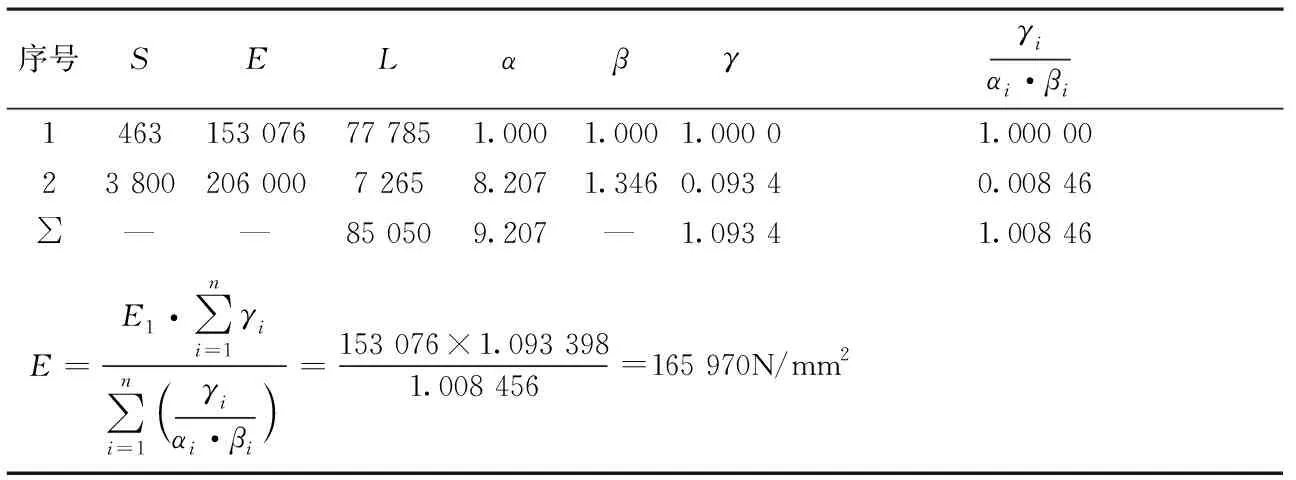
表4 按索的实际E1值求出的中部调节端以上竖索体系的E

表5 按索的理论E1值求出的中部调节端以上竖索体系的E

当E1=153 076N/mm2时，中部调节端变形按公式计算的E=165 970N/mm2。当E1=160 000N/mm2时 ，中部调节端变形按公式计算的E=173 411N/mm2。

由表6可看出，采用索厂家提供的索的弹性模量计算的竖索体系变形与采用经现场线弹性验证后得出的索的实际弹性模量计算出的竖索体系的变形存在4～5mm偏差，与前述未进行索的现场线弹性验证时就进行计算和张拉的工作过程中发现的调节端偏差规律一致。从而可知，竖索体系的弹性模量与理论值间的差异是由索的自身弹性模量的差异造成。

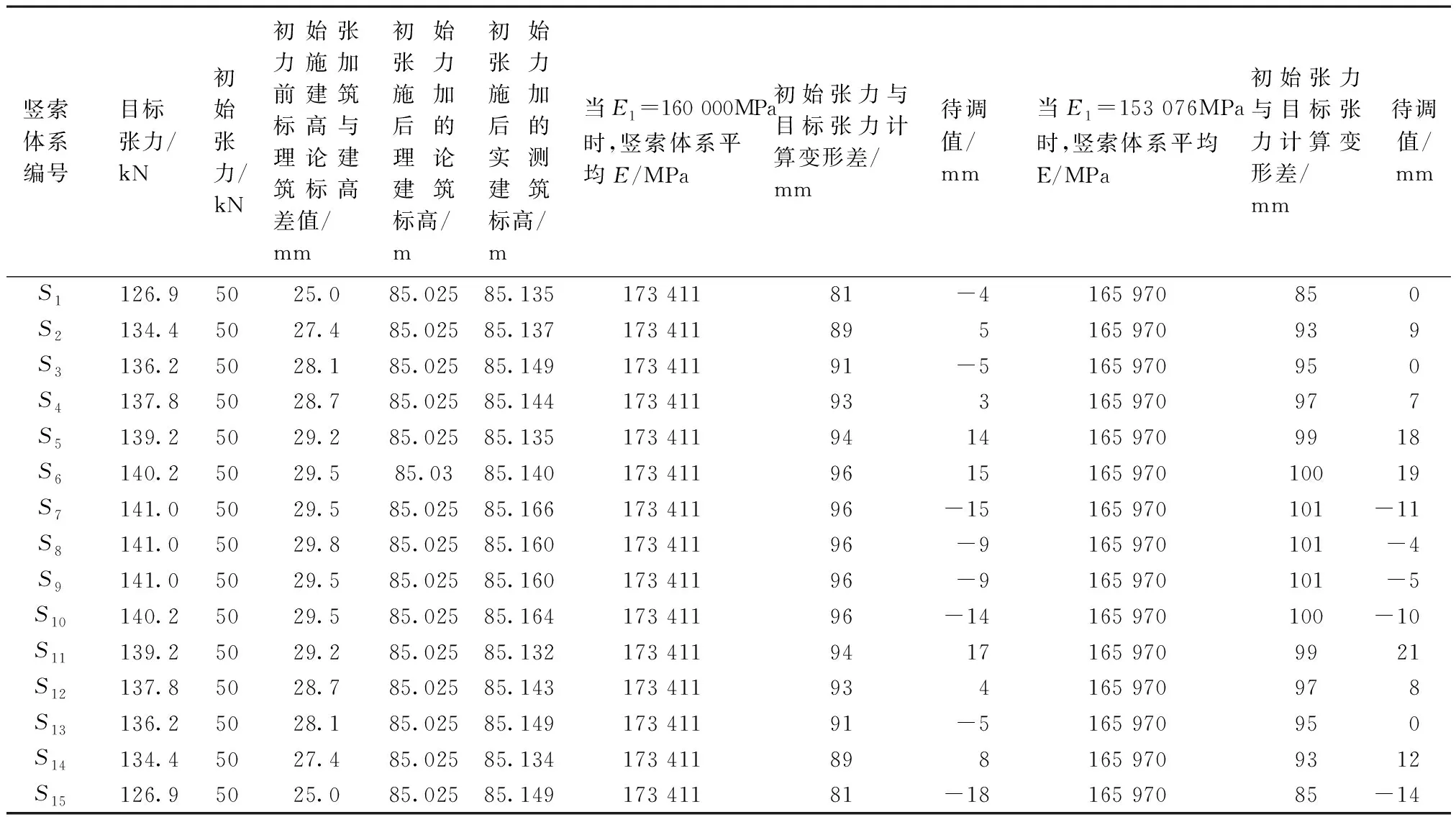
表6 分别用理论E1值和实际E1值计算的竖索体系的E值计算的竖索体系变形调节值

4 计算底部调节端调节值时E值的计算和分析

有了简化的竖索体系的综合弹性模量的计算公式，除了可计算中部调节端在设定拉力的变形预调节数值以外，还可对竖索体系中的任意位置在设定拉力条件下的变形数值进行计算。本项目除了在中部设置调节端进行预调节和过程微小调节外，为了使张拉过程方便操作，将张拉端放在底部调节端，因此在中部调节端调节的同时，还需对底部调节端进行调节，同样需应用上述原理和公式进行受力变形计算。

当计算底部调节端调节数值时，竖索体系的长度在中部调节端以上长度的基础上，又增加了中部调节端下部竖索体系的长度，需考虑长度变化带来的应用整个竖索体系的弹性模量计算内容的调整。

选用不同索的弹性模量数值计算出的竖索体系的弹性模量数值不同，如表7～10所示。

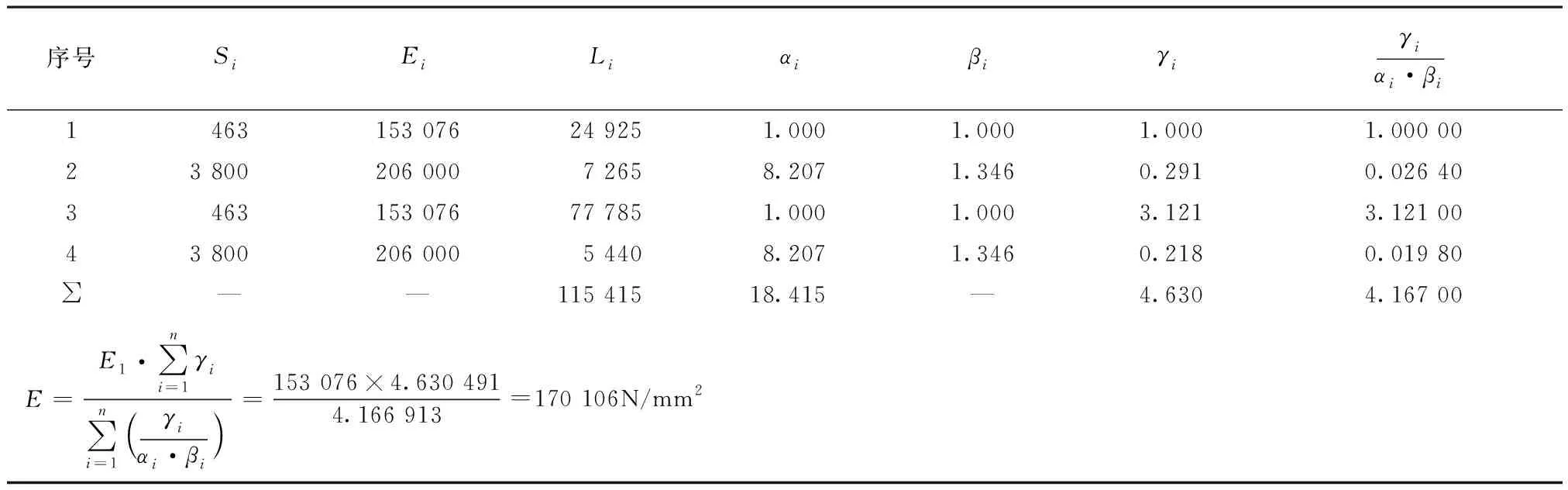
表7 索在实际E1状态下使用简化公式计算的竖索体系的综合E值(1)

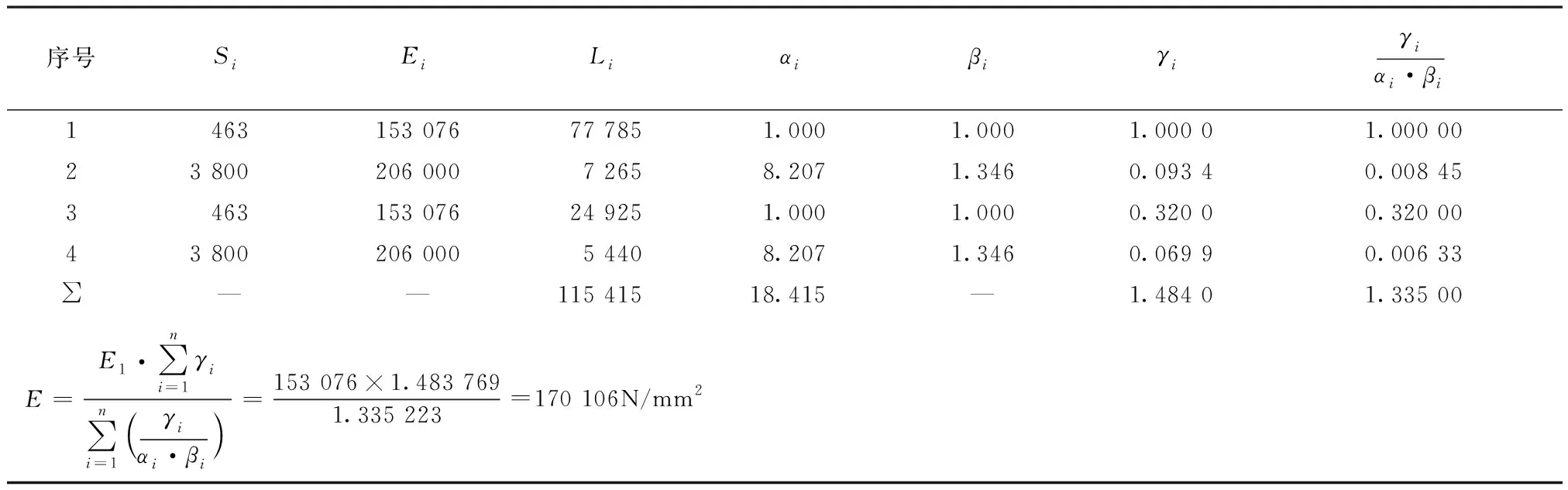
表8 索在实际E1状态下使用简化公式计算的竖索体系的综合E值(2)

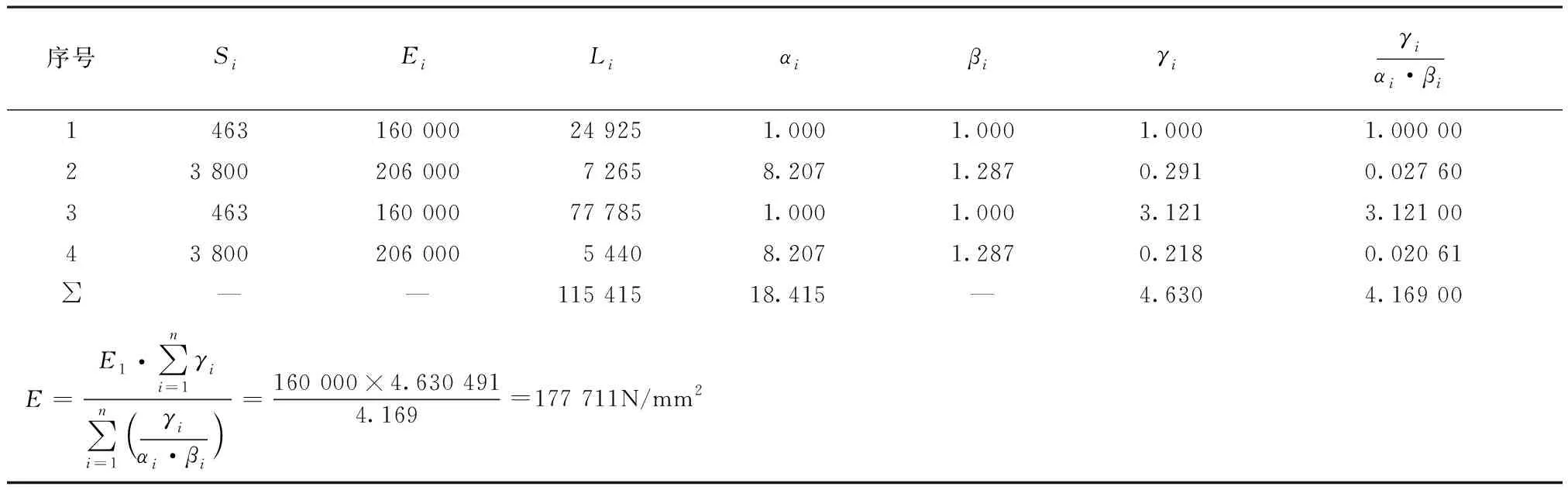
表9 索在理论E1状态下使用简化公式计算的竖索体系的综合E值(1)

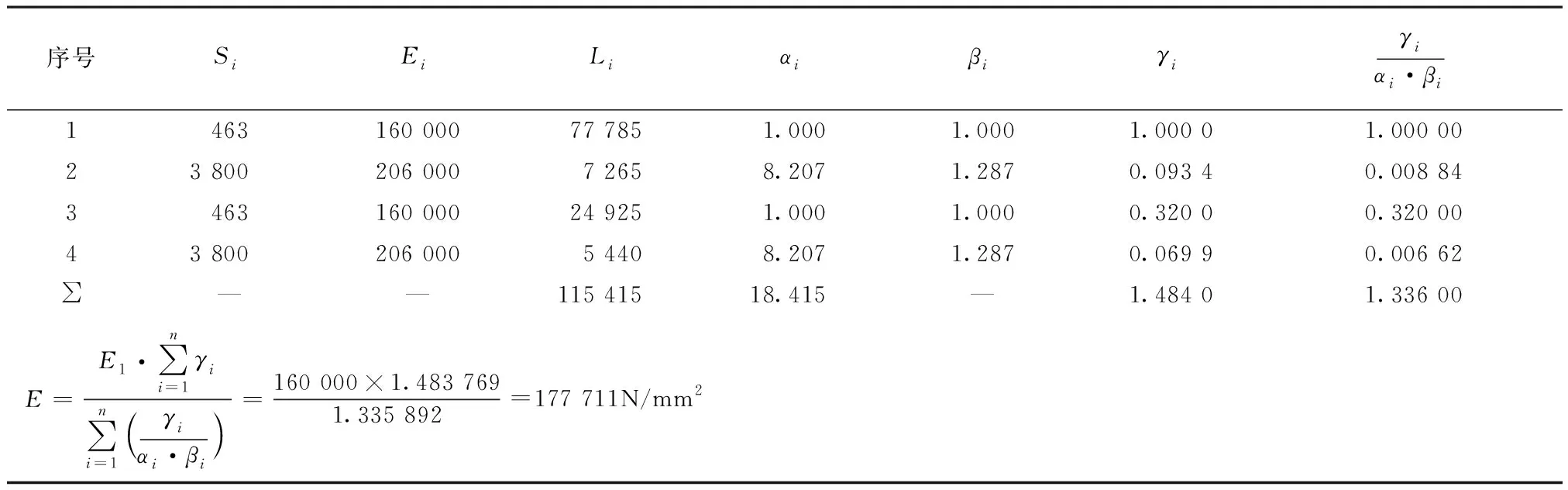
表10 索在理论E1状态下使用简化公式计算的竖索体系的综合E值(2)

根据胡克定律公式的特征，逐级计算出按顺序张拉后的竖索体系底部调节端位置的变形值，如图5所示，图中由上至下分别对应表11中2种不同弹性模量状态下玻璃荷载施加以后竖索体系底部调节端的变形值，张拉到设计预张力时玻璃荷载施加以前竖索体系底部调节端的变形值，施加50kN荷载后竖索体系底部调节端的变形值。

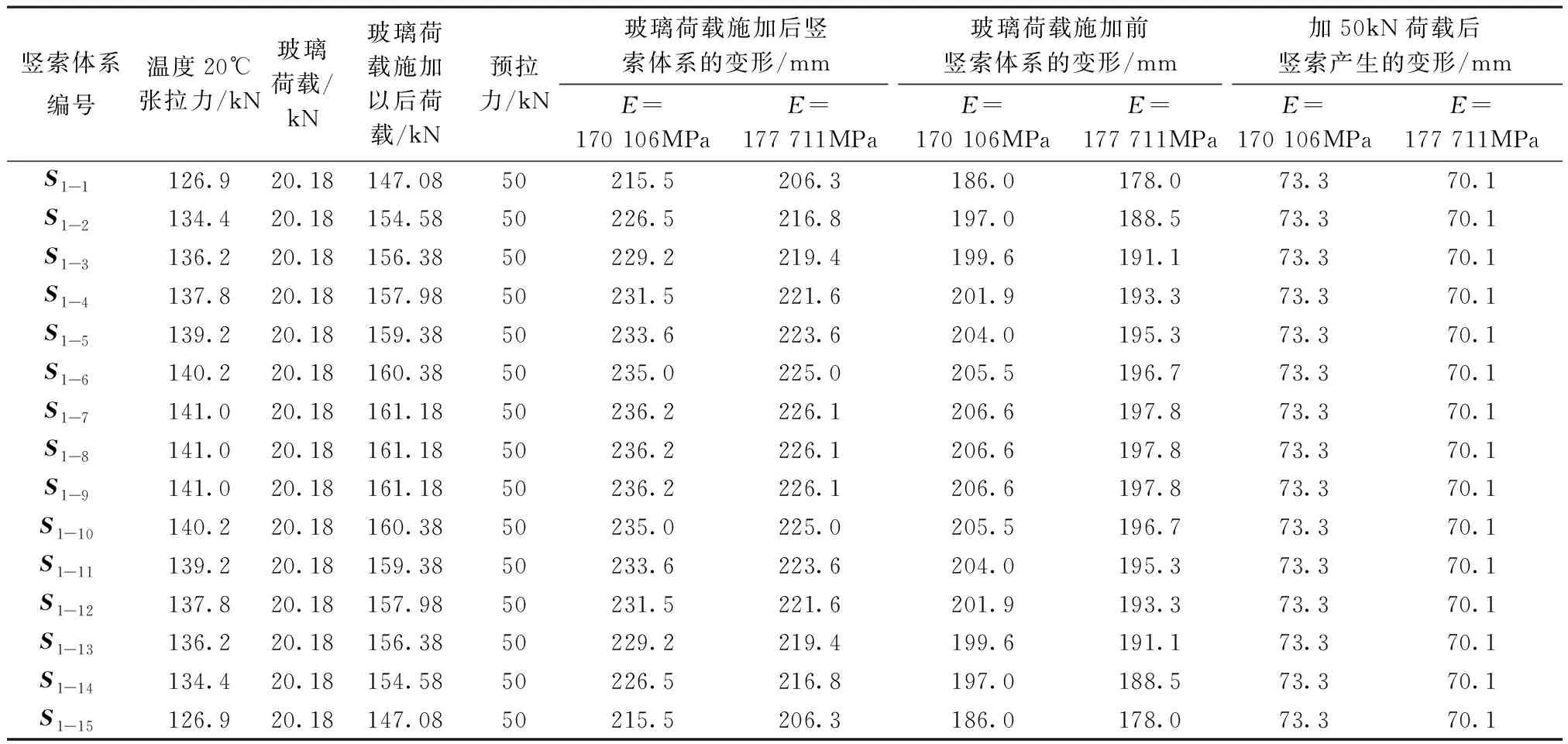
表11 竖索体系在不同综合计算E值状态下受力变形计算

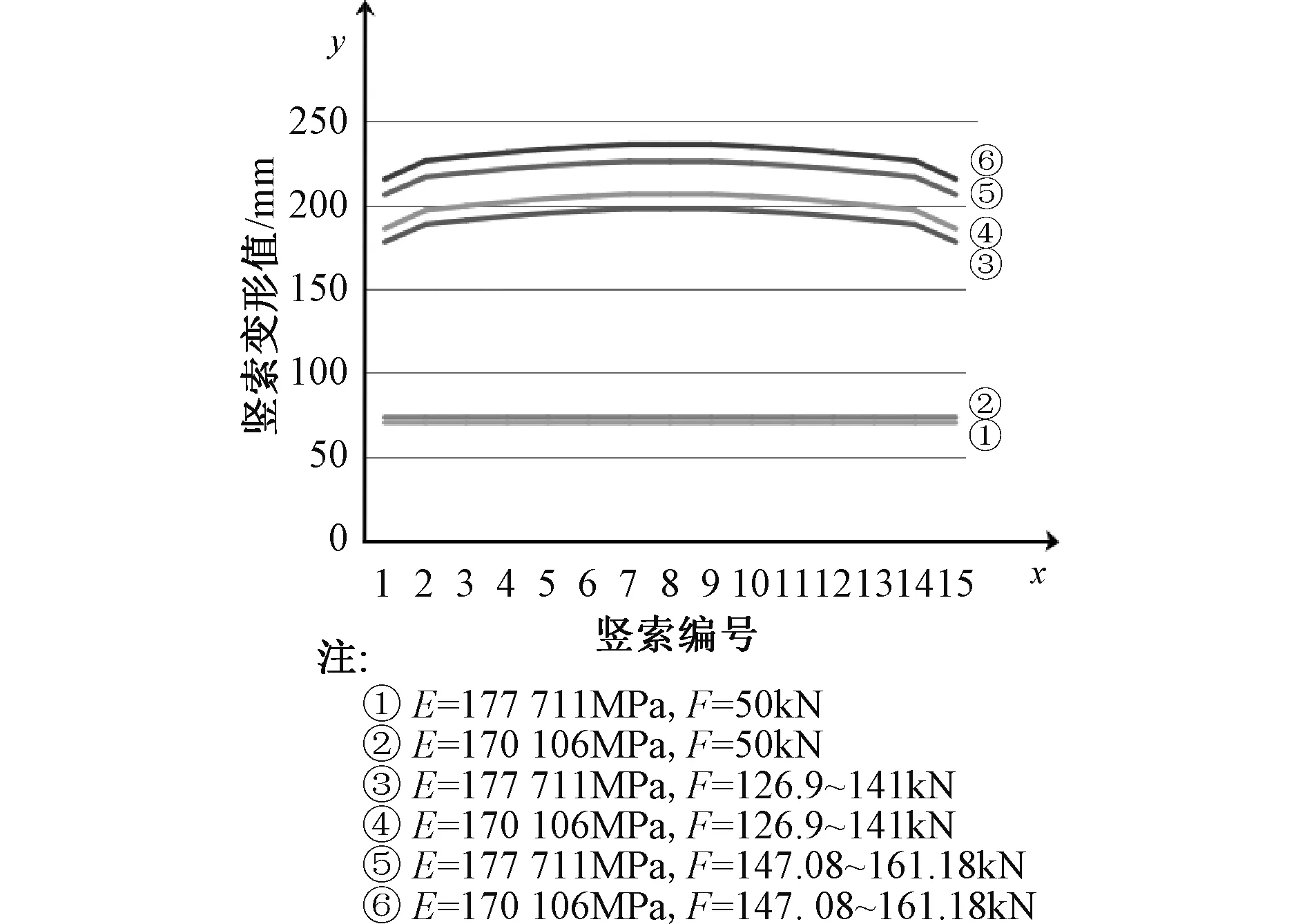
图5 竖索体系在2种弹性模量状态下受拉变形对比

对比分析后，依照调整后竖索体系的弹性模量数值计算出的中部调节端的变形值进行预调节，依照计算出的底部调节端变形值进行张拉，实现了竖索体系在拉力和变形的动态平衡状态下，竖索体系中设定位置的精准调节，顺利完成了施工。

5 结语

1)通过实际工程的应用和验证，串联弹性体组成的竖索体系变形仍可应用胡克定律计算，对变形计算过程中使用的竖索体系的弹性模量，可根据组成竖索体系的弹性体的特性，利用简化公式计算得出。

2)计算竖索体系的弹性模量的公式由于忽略了弹性体串联连接构造的影响，只是一个近似解，但精度可满足指导工程施工的要求。

3)竖索体系计算时，应挑选长度占比大、弹性模量小、截面积小的材料作为基准材料，这种做法使得应用简化公式计算的竖索体系的弹性模量更准确。

4)索体的实际弹性模量数值与厂家给定的弹性模量数值可能存在偏差，需在现场对竖索的弹性模量做张拉验证，这样才能得到相对准确的索的弹性模量，进而可应用简化公式求得竖索体的弹性模量，为应用胡克定律计算竖索体系变形提供基础依据。

5)利用线弹性变形理论和简化公式计算竖索体系时，需注意计算点位置也是影响竖索体系变形量和调节值的关键因素，需结合实际情况使用相应位置到基准点的竖索体系长度。

6)在本例竖索张拉过程中横向线应变对截面积几乎无影响，当竖索横向线应变对截面积有明显影响时，需考虑横截面面积变化对索和竖索体系带来的影响。

7)文中计算弹性模量的表格中考虑到小数点后只保留3位有效数字，与汇总公式中每项数据都保留了小数点后多位时的计算结果存在0.04%的微小偏差，工程应用中可忽略，后续表格中的数据分析仍采用汇总公式的计算结果。

通过理论推导和实践应用，本文较详细地阐述了现场对索的线弹性验证的方法，推导出可应用的竖索体系的弹性模量简化计算公式，使得现场可应用简化计算的弹性模量计算竖索体系的受力变形，方便作业调整。