基于多因素融合与ARIMA的电力物资预测
2022-08-02黄晓明余乘龙
丁 靖,黄晓明,余乘龙
(1.国网宁波供电公司,浙江 宁波 315000; 2.国网宁海县供电公司,浙江 宁海 315600)
应急物资的合理预测,有利于相关部门确定应急物资的需求量并采取有效的措施,有力地展开救灾抢险工作,提高人民的生活保障。在物资需求预测的研究上,国内外学者进行了一些研究工作。主要的方法有时间序列法、回归分析法、神经网络预测、基于支持向量回归的预测法、案例推理法。随着社会的不断发展,对物资需求预测的精度要求越来越高,这就要求科研人员不断探索新方法,不断拓展预测相关的理论研究和应用研究。
Elxagal.H等[1]改进人工神经网络,在分析公用事业天然气的需求特性的基础上,提出分阶段使用神经网络,最终可提高预测模型的精度,其缺点在于神经网络的计算复杂度较高和参数选择较为困难。Venkatesh等[2]提出ATM机现金需求的预测模型,首先为每个ATM机建立时间序列模型,然后再利用聚类并建立神经网络来预测现金需求。一些学者利用统计方法来对物资需求进行预测,如Del Ninno,Dorosh,Smith等[3]利用集成分析Balaguer,Palomares,Soria等提出自回归滑动平均法,然而物资的需求存在非线性和不规则性,传统的统计方法和计量方法不能奏效。在国外学者进行的大量预测模型的研究工作中,对某些物资的需求量的预测表现能力尚可,例如需求量满足一定的分布,或者需求量和特征的相关度高等。
基于以上分析,本文首先不同影响电力物资需求的主要因素进行分析,得到多因素融合的电力物资特征主体。进而利用自回归移动平均模型(ARIMA)对不同影响因素特征下的电网物资需求进行预测,预测模型能够很好地利用需求历史数据,从而解决预测过程中地非线性和不规则形问题,具有一定实际价值。
1 基于多因素融合的电力物资特征分析
在进行预测模型的训练之前,首先需要对事故事件中的电力应急物资提取有效的特征。分析了电力应急物资的需求特点、分类和影响因素,并充分利用这些影响因素,提取出最有效的特征向量,这样训练的预测模型才能具有良好的性能。再对这些灾害事件下的电力应急物资需求影响因素进行详细的分析,得出影响物资需求量的主要因素,然后按照一定的规则组成事故事件中的电力应急物资特征向量。
1.1 电力物资需求特点
应急物资是指在应急物流的实施和保障中所采用的各类物资[4]。与一般应急物资相比较,电力应急物资的需求更难确定、时间响应要求更高,其特别之处主要表现在以下几个方面[5]。
(1)受领任务紧急,偶然状况发生概率高。台风等自然灾害的发生要求电力公司必须立即做出应急响应。遭受自然灾害破坏的地区,其电力公共设施损坏严重。电力应急物资的需求无法准确的估计,会使得抢修工作难以进行,以上问题会给电力应急物资的供给配送引起巨大的难度。
(2)以恢复电力生产为主,时间效益第一。电力应急抢修的目标是立即恢复供电,以确保受灾地区的居民人身安全,最大化的降低社会损失。
1.2 电力物资需求的影响因素
1.2.1 风力对电力物资需求的影响
狂风对电力设备会造成严重的影响,主要表现为:①断线。一定风速超过电线所能承载的极限时的断线,大风刮起的物体也有可能毁坏电线。②倒塔。由于台风所带来的风力,导致杆塔受力不平衡,极易造成杆塔横倾或纵倾,从而引发倒塔。③风偏闪络。大档距或大弧垂导线在风向与导线轴向夹角大于45°时易产生较大风偏,将导致导线与周边物放电并增加断线的概率。
1.2.2 暴雨对电力物资需求的影响
暴雨对地区的电力设备会造成严重的破坏,其主要表现为:①发电站。主要影响水电站的水工建设和火电厂的引水渠道、煤场等。水电站因暴雨造成的水势过大、管道堵塞,造成电站直接停机。而在火电厂,降雨则会严重影响煤的湿度。②变电站。暴雨洪水极易冲刷处于地势较低的变电站,这将会导致设备异常情况频发、通信系统故障率提升。③杆塔。在暴雨的冲刷下,处于滑坡、河沟的杆塔极易倒塌。
1.2.3 电网建设对电力物资需求的影响
恶劣天气对电力系统的破坏程度的不同与当地的电网规模水平密切相关,显然,工业城市的用电量就比农业城市用电量大。电力应急物资的需求量主要以事故灾害中被毁坏的数量为根据,通常情况下,电网规模水平越大的,被破坏的也越大。地区电网建设规模指标可以反映出某地区电网整体规模水平,但是对此指标进行定量计算却是很大的难题。目前,有关此类工作的文献很少。李欣然等[6]基于层次分析法原理建立一套综合评估配电网建设规模的评价指标体系。其提出的指标层的指标主要包括110 kV变电站总容量、110 kV变电站总个数、110 kV变压器总台数、10 kV出线总回路数、10 kV线路总长度、10 kV配电总容量、10 kV配电所总个数、10 kV配电总台数等8个指标。通过参照相关文献的方法,可以得出各地区电网规模值,将其作为台风事件中的电力应急物资特征向量的一个维度。
2 基于ARIMA的电力物资预测
2.1 数据平稳性检验
使用ARIMA模型要求时间序列必须是平稳的,所以第一步是对原始数据进行平稳性检验。假设当一个自回归过程如下所示[7-9]:
yt=byt-1+a+εt
(1)
如果滞后项系数b为1,就称为单位根。当单位根存在时,自变量和因变量之间的关系具有欺骗性,因为残差序列的任何误差都不会随着样本量(时期数)增大而衰减,也就是说模型中残差的影响是永久的。这种回归又称作伪回归。如果单位根存在,这个过程就是一个随机漫步(random walk)。因此,本文模型使用ADF和KPSS来检测数据的平稳性。
2.2 基于ARIMA预测模型阶数
ARIMA预测适用于实际数据具有一定复杂性的预测模型,其数学模型为:
yt=a+b1yt-1+b2yt-2+…+bpyt-p+εt-θ1εt-1-θ2εt-2-θqεt-q
(2)
式中,yt为随机变量,bp为自回归系数,εt为随机干扰项,θq为移动平均系数,p、q则为ARIMA模型的阶数。
对于p、q的求解,文中分别采用自相关函数和偏自相关函数求解,具体方法可参考文献[10]。延迟k阶的自相关函数:
(3)
式中,N为序列长度。由{yt}的前k个时刻的数据估计yt的最小方差,其中的第k个系数akk为偏相关函数。
(4)
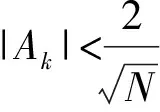
2.3 模型残差检验
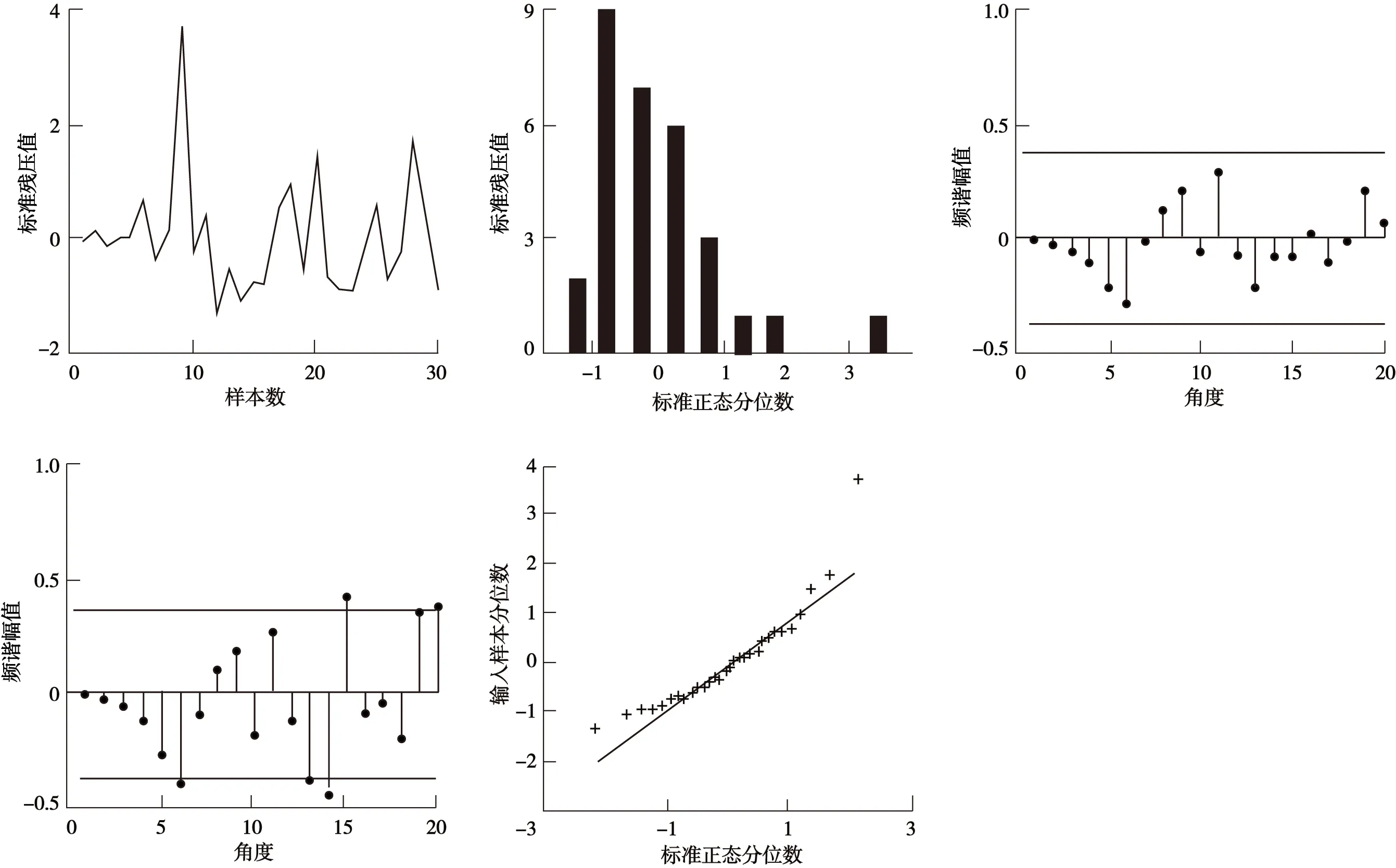
为了确保确定的阶数合适,还需要进行残差检验。残差即原始信号减掉模型拟合出的信号后的残余信号。如果残差是随机正态分布的、不自相关的,这说明残差是一段白噪声信号,也就说明有用的信号已经都被提取到ARIMA模型中了。
对于文中的用电需求预测模型进行残差检验,需要检验εt(t=1,2,…,N)是否为白噪声信号,由式(2)可得:
εt=yt-(b1yt-1+b2yt-2+…+bpyt-p-θ1εt-1-θ2εt-2-θqεt-q)
(5)
上述误差序列的检验量为:
(6)
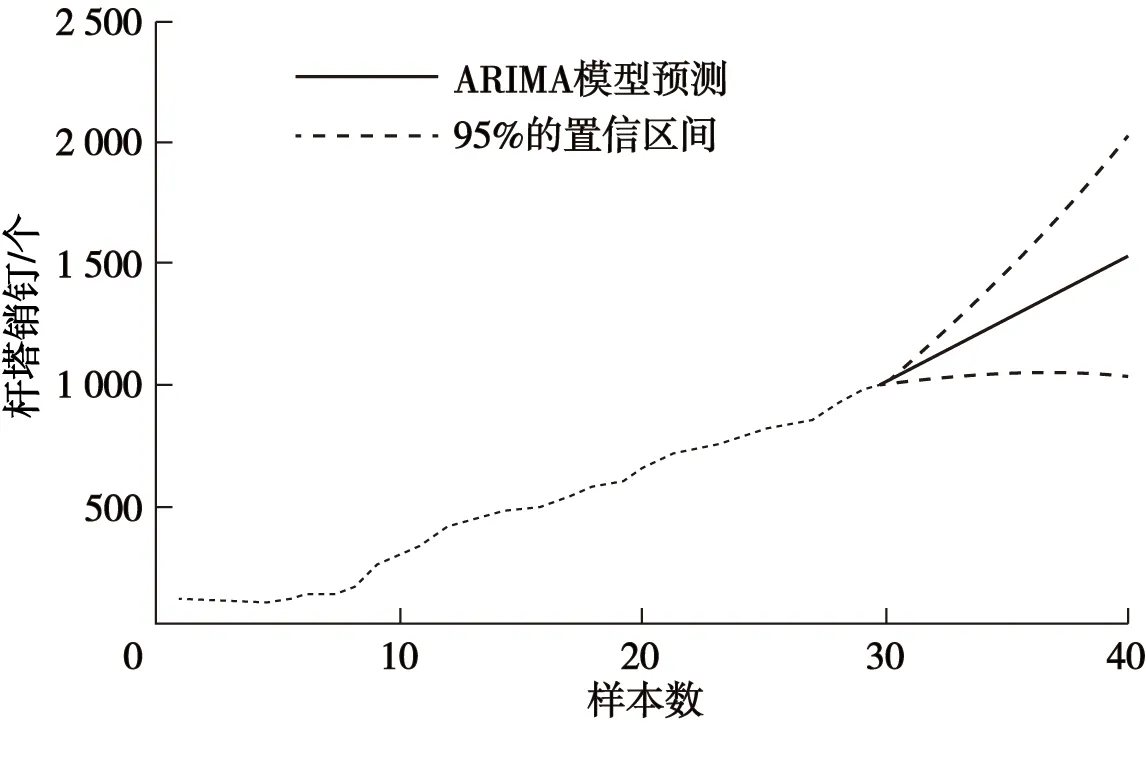
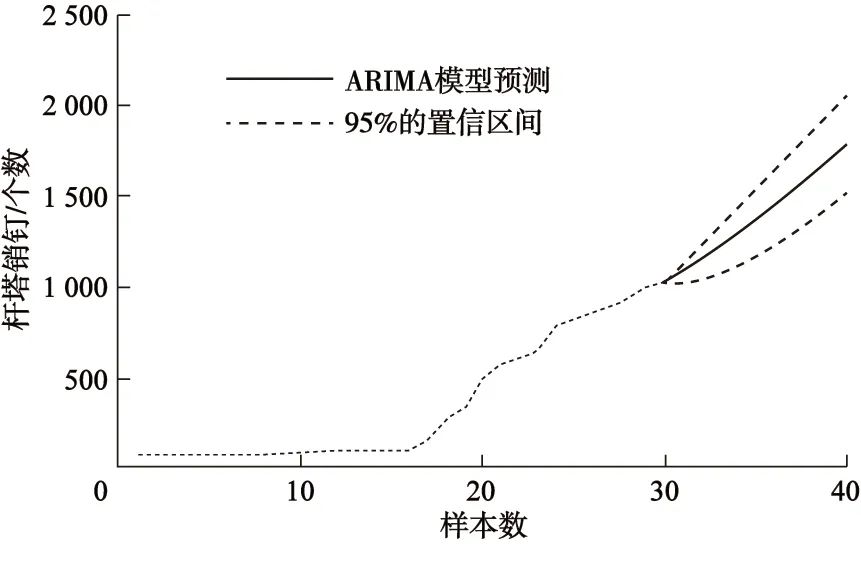
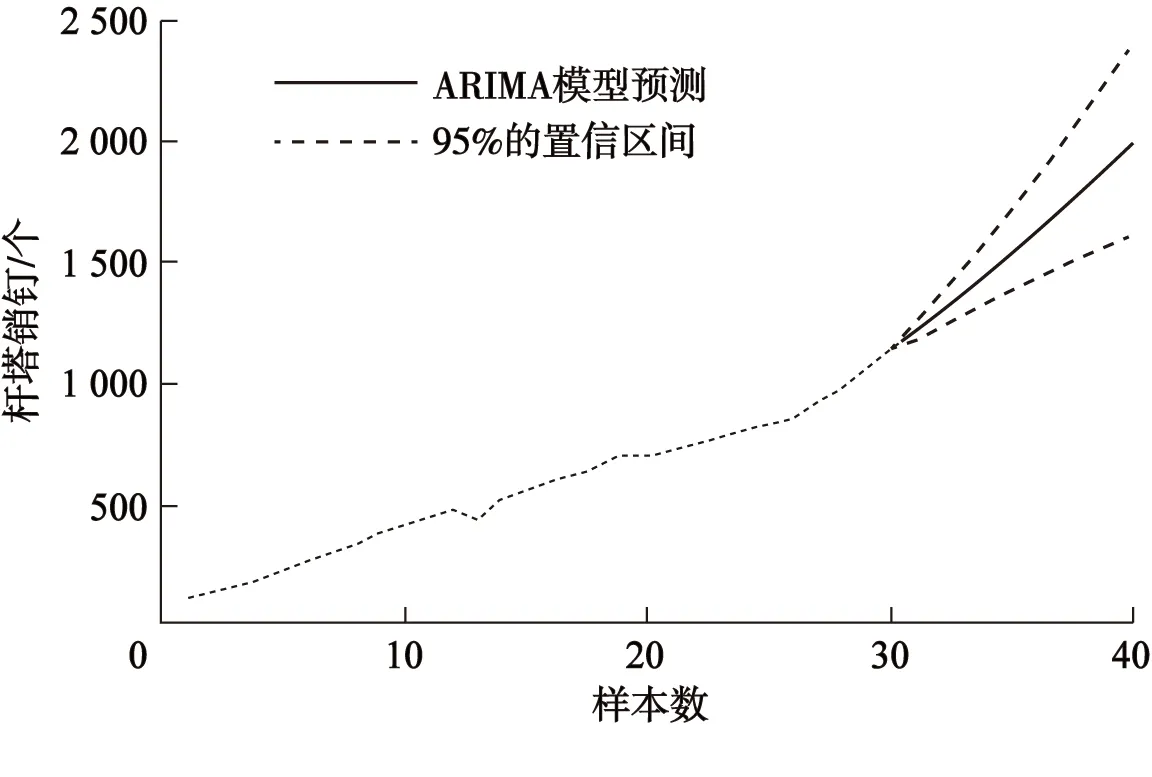
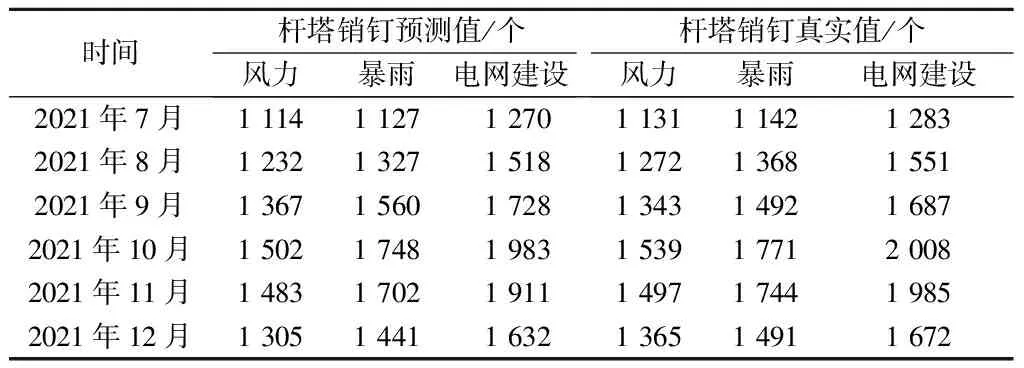
式中,Q服从χ2(M)分布,M 文中假设M=N/8,通过设显著性水平α,利用查表法找到P={Q>χ2(M)}=α时的χ2(M)。仅当Q<χ2(M)时,ARIMA模型才可使用。 基于ARIMA模型的电力物资需求预测需要用到历史用电数据,同时需要指出的是若某一年发生极大规模天气灾害,或者大规模电网建设,有可能导致预测精度受到影响,导致最终的预测值发生偏差,综合模型自身也有相应的精度水平,本文设置电力物资需求预测的置信区间,在运用模型计算出电力物资需求预测值的同时,也会给出预测需求值在给定置信区间内的波动范围,相比于传统的预测方法,本文中的基于ARIMA的电力物资需求预测更具有实用性和可靠性。 本文以浙江宁波市从2019—2021年共计36个月的110 kV和220 kV线路杆塔销钉电力物资数据作为算例分析的数据源,首先对不同影响因素下的电力物资需求进行分析,并将它们进行归类,能够得到海口市在多因素融合下的电力物资特征分析。 接下来,本文再对3种不同影响因素主体下的电力物资需求进行ARIMA模型预测。本算例中,将前30个月的电力物资需求数据作为历史数据输入,将后6个月数据作为预测数据,通过将预测值和实际值相比较来检验本文所提模型的有效性。 首先针对风力影响因素,其仿真结果如图1所示。首先是模型的平滑性检验和残差检验,由图1能够看出,在ARIMA预测模型下,历史数据取2阶差分时趋于稳定,同时由图1可知,ARIMA预测模型的阶数p=2,q=1,最后是残差值检验,易知该预测模型的残差值是符合随机正态分布的。因此,ARIMA预测模型可用。 由以上分析可知,针对风力影响下的ARIMA预测在电力物资需求预测中是可行的,于是得到预测值大小,如图2所示。 本文中的ARIMA预测模型还设置了95%的预测值置信区间,也即预测值围绕预测精准值波动,并落在95%的预测置信区间之内,因此模型有效性也得到了验证。 然后是针对暴雨和电网建设这两个影响因素下的电力物资预测,其模型的差分阶数和p、q值分别见表1。 图1 风力影响下电力物资需求ARIMA预测模型检验Fig.1 ARIMA prediction model test of power material demand under the influence of wind 图2 风力影响下电力物资需求ARIMA预测结果Fig.2 ARIMA prediction results of power materialdemand under the influence of wind 表1 暴雨和电网建设影响下的预测模型检验Tab.1 test of prediction model under the influence ofrainstorm and power grid construction 由表1可知,针对暴雨和电网建设影响因素下电力物资需求的ARIMA预测模型均满足随机正态分布,因此是可行的。再针对这2个结构进行ARIMA模型电力物资需求预测,得到图3和图4。同样,针对这2个结构,预测模型也设置了95%的预测值置信区间。上述关于暴雨和电网建设影响下电力物资需求变化趋势和预测结果符合实际。 图3 暴雨影响下电力物资需求ARIMA预测结果Fig.3 ARIMA prediction results of power material demand under the influence of rainstorm 将不同影响因素下的电力物资需求ARIMA预测结果与实际值相比较,其对比结果见表2。 图4 电网建设影响下电力物资需求ARIMA预测结果Fig.4 ARIMA forecast results of power material demand under the influence of power grid construction 表2 基于ARIMA模型预测值和真实值比较Tab.2 Comparison between predicted value and real value based on ARIMA model 由表2可以看出,在风力和暴雨影响因素下的电力物资需求预测在2021年的后6个月的预测值与真实值的偏差均在5%以内,也即预测值落在ARIMA模型的置信区间内;但在2021年的8月、9月,模型的预测值与实际值偏差较大,超出了95%的预测置信区间,这是因为ARIMA预测模型是按照历史数据进行预测的,在这2个月内,该市出现较大规模的极端天气现象,而ARIMA模型无法预测短时间内的非常规增减趋势,因此出现差值较大的情况。随后在后续月份,预测值再次回归正常的增长趋势,从而ARIMA预测模型的预测值与真实值的偏差又在5%以内,也即预测值落在ARIMA模型的置信区间内。而对于电网建设,其相应受影响的电网物资需求增长趋势始终较为平稳,这是由于地区电网发展相对平稳。因此,ARIMA模型的预测值和真实值的偏差几乎都在5%以内。 由以上分析可知,本文的在多因素融合下的电力物资需求预测模型具有一定的使用价值。 本文首先对电力物资的主要影响因素进行归纳,得到3种不同的主要影响因素,并将它们进行归类,从而得到简化的电力物资影响因素,实现了不同影响因素下的电力物资需求分析;然后将ARIMA预测模型用于对不同影响因素的电力物资需求预测。最后,运用算例验证ARIMA预测模型的有效性。结果表明本文中的模型具有一定的实用价值。2.4 用电需求预测
3 算例分析

4 结论
