改进粒子群算法的输配电网分布式电源规划研究

孙才华，刘 强

(国网河南省电力公司，河南 郑州 450000)

以往用于电力产业的能源多数清洁性较差，并且不可再生与重复利用，这不仅造成了能源资源的浪费、对环境产生了污染，同时也与国家“节能环保”的政策背道而驰[1]。在节能环保的时代大潮下，将可再生能源应用到电力产业中，不仅能实现资源的有效利用，同时还能避免严重的环境污染现象[2]。由于很多可再生能源都不能被大规模地集中应用于电力产业中，而分布式电源作为一种小型模块电源装置，能够最大程度地利用电热能，并且可以对输配电网中的能源进行二次利用，将可再生能源很好地应用到电力产业中[3]，自然而然成为各大电力企业有效利用可再生能源的重要手段。近年来，国内外诸多学者对分布式电源在电网电源规划中的应用进行了研究，如潘霄等[4]基于需求相关性分组预测的分布式电源规划方法的研究，鄢晶等[5]基于向量序优化的分布式电源规划方法的研究。这些研究都取得了相当可人的成绩，在减少环境污染现象的产生的同时，提高了电网运行的稳定性，但是其在寻求电源规划最优解时的速度较慢，耗时较长，无法满足分布式电源在电源规划中对速度与耗时方面的要求[6]。

改进粒子群算法具有较快的收敛速度，在求解问题时耗时少。本文提出基于改进粒子群算法的输配电网分布式电源规划方法，在进行输配电网电源规划时，能够快速寻优电源规划的最优解，降低输配电网运行成本，更能满足实际电网运行需求。

1 分布式发电技术

1.1 风力发电技术

风力发电主要有离网式、互补式和并网式3种运行方式。

(1)离网运行方式。独立于公共电网，利用储能设备将风机转化的电能进行储存，需要用电的时候，再将电能输出供给负荷用户使用。但此种方式不确定性较大，供电系统的稳定性差。风电系统独立运行的结构如图1所示。

图1 独立风电系统结构Fig.1 Structure of independent wind power system

(2)互补运行方式。指风电与其他发电方式相结合进行互补供电，不仅可以改善风力发电的不稳定性和间歇性，而且可以发挥可再生能源的优势，延长储能设备的使用时间。

(3)并网运行方式。指风力发电机组与电网连接，向电网输送有功功率，并且吸收或发出无功功率的风电系统，目前变速恒频方式是并网运行使用的主要方式，风电系统并网运行的结构如图2所示。

图2 并网风电系统结构Fig.2 Grid connected wind power system structure

1.2 太阳能光伏发电技术

当前光伏发电主要为独立光伏系统及并网光伏发电系统，独立光伏发电系统结构如图3所示。

图3 独立光伏发电系统示意Fig.3 Schematic of independent PHOTOVOLTAIC power generation system

并网光伏发电系统如图4所示。

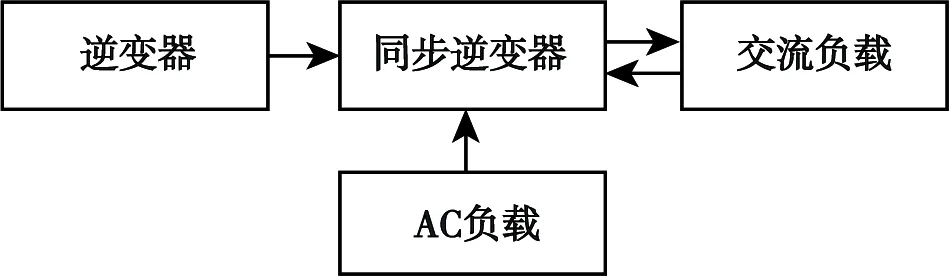
图4 并网光电系统示意Fig.4 Schematic of grid-connected photoelectric system

2 输配电网分布式电源规划方法

2.1 输配电网分布式电源规划模型

2.1.1 总投资与运行成本目标函数

将分布式电源应用到输配电网中，会使得输配电网的运行成本提高[7]。为了达到合理控制输配电网的运行成本的目的，本文将分布式电源总投资与运行成本最小目标函数用公式定义为：

(1)

式中，pg、n分别为输配电网中分布式电源的总容量与设备使用的年限；r为贴现率；c1为投资成本；c2为运行成本。

2.1.2 有功网损

输配电网应用分布式电源后，由于分布式电源与用户侧的距离较近，网损很大概率上会降低[8]，因而本文用公式将分布式电源有功网损最小目标函数定义为：

(2)

式中，Ploss为系统的有功网损；l、ik分别为支路数与支路电流；rk为支路电阻。

2.1.3 电压稳定裕度目标函数

输配电网应用分布式电源后，对一些负荷节点的电压很大概率上会造成一定影响，主要表现为电压的不稳定。为了达到衡量电压稳定性、对分布式电源应用到输配电网容量以及位置进行有效合理限制的目的[9]，本文提出电压稳定裕度目标函数，为：

(3)

式中，Unload、Ue分别为负荷不等于0的电力节点电压值与节点负荷期望电压值。

2.1.4 约束条件

(1)容量约束条件为：

(4)

式中，l、n分别为总支路和分布式电源个数；ps、pdgi分别为发电厂及第i个分布式电源注入的有功；plgi为支路i的有功负荷。

(2)电压约束条件为：

|vi|min≤|vi|≤|vi|max

(5)

式中，|vi|为i节点的电压幅值；|vi|max、|vi|min分别为电压的上限、下限。

(3)电流约束条件为：

|Ii|≤|Ii|max

(6)

式中，|Ii|为代表每条支路电流；|Ii|max为允许范围内的电流上限。

2.2 基于粒子群算法的模型求解

2.2.1 粒子群(PSO)算法

为求得输配电网分布式电源规划模型的解，需利用算法迭代计算，得到全局最优解。粒子群算法是一种群优化算法，以可行解作为粒子，在搜索可行解的过程中模拟鸟类觅食的行为。寻找食物过程中，每个粒子都拥有自己的位置和速度，并且各个粒子根据适应函数值和速度来对它自身的飞行方向进行调整，这样能够保证向食物的位置飞行。在向食物靠近的过程中，所有粒子能够记忆自身位置以及自身最佳位置，并且在运动过程中对他们进行调整。粒子群算法具有结构简单、参数少易实现、收敛速度快效率高的优势，考虑将其应用于输配电网分布式电源规划模型求解。

2.2.2 改进粒子群算法

由于基本的PSO粒子群算法在求解分布式电源规划模型时，因其自身的局限性，容易使分布式电源规划模型的解精度不够，并且当求解过程比较复杂时，其收敛速度较慢[10]。为减少上述状况的发生，采用MPSO算法寻找分布式电源规划模型的最优解。惯性系数的初始、结束值分别用θmax、θmin描述。iter、itermax分别为此时、最大迭代数目。θ的迭代计算为：

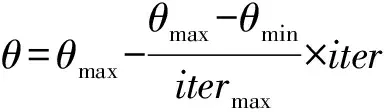
(7)

在用粒子群算法进行配电网分布式电源规划模型求解的过程中，会出现某些粒子向最优粒子位置靠近的现象，从而使算法陷入局部最优，收敛时间过早，从而影响对配电网分布式电源规划模型的求解[11-12]。为了避免类似现象的发生，本文在进行配电网分布式电源规划模型求解时，当种群的全局极值在一定次数的迭代之后，依旧无法得到提高，则在保留全局极值的条件下，再一次对部分粒子进行初始化操作[13-14]。

2.2.3 粒子群算法求解流程

(1)输入输配电网分布式电源原始数据，获取包括系统节点、支路、电压、电流等主要信息，并对相关参数进行粒子群初始化操作[15]。

(2)将迭代粒子的初始速度设置为0，并对初始粒子的最优解最大迭代次数进行限定。

(3)计算粒子群中粒子的潮流、网损，并根据分布式电源规划模型的目标函数对粒子的适应值进行分析；将最小的适应值与及其位置作为实时的最优解与认知最优解。

(4)根据式(7)以及式inter=inter+1对惯性因子、计数器进行更新，通过公式求解粒子速度、位置。如果粒子的速度高于最大速度，或者低于最小速度，就把最大速度、最小速度当作粒子的速度。

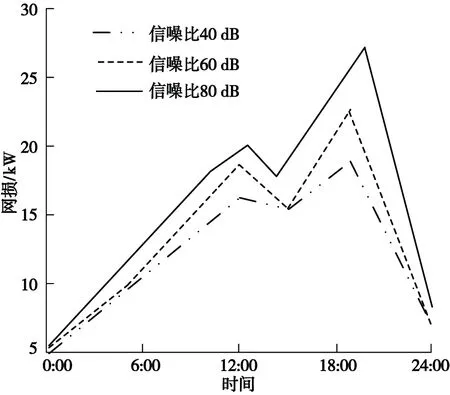
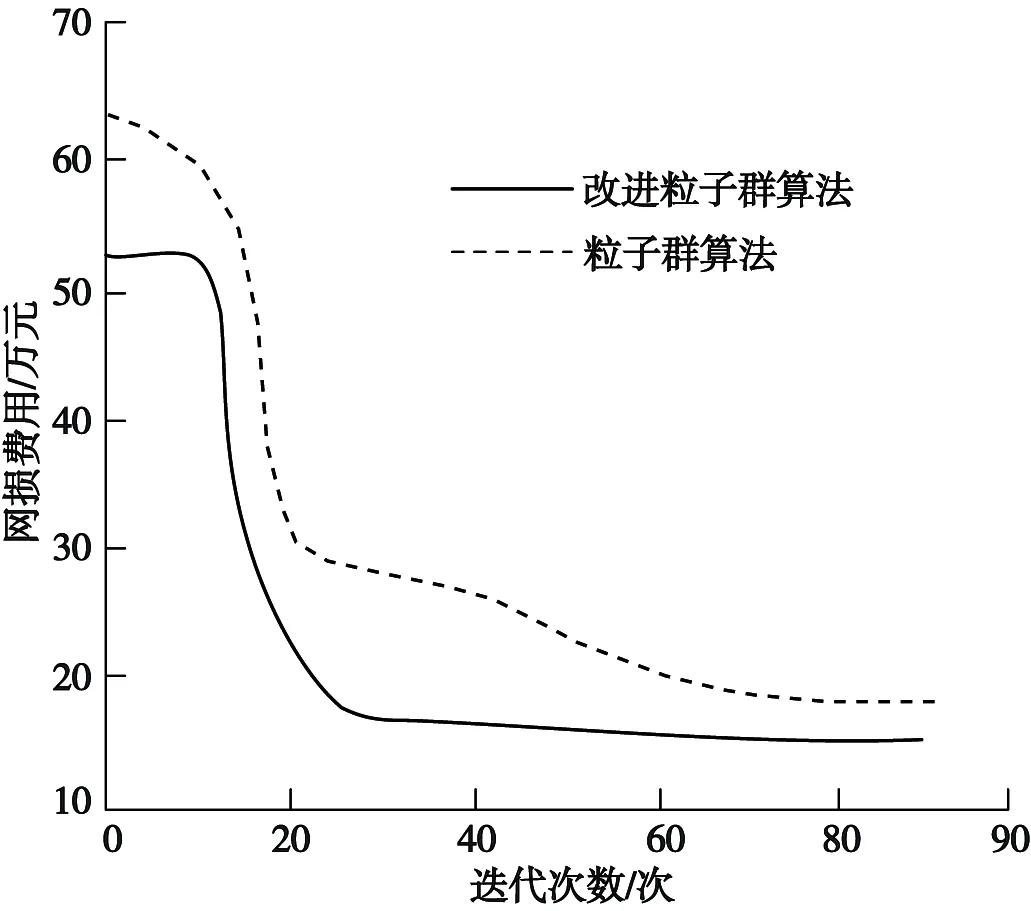
(5)重新计算粒子群中粒子的潮流、线损，分析粒子的适应值。用F(xi)代表各粒子的适应值，pbest代表当前个体最优解，并将F(xi)与pbest进行比较，如果F(xi)

(6)将当前迭代次数iter与最大迭代次数itermax进行比较，如果达到最大迭代次数，则进行下一步操作，反之从第(4)步开始重新进行相关粒子操作。

(7)得到分布式电源规划模型的最优解。

3 实验与论证

本文以某市某大型供电公司为实验对象，应用具有33个节点的IEEE配电网系统对其输配电网分布式电源规划进行模拟测试，验证本文方法的可行性与有效性。拥有33个节点的节点系统网络结构如图5所示。

图5 33节点系统网络结构Fig.5 Network structure of 33 node system

应用本文方法得到的33节点系统网络结构中各节点的电压稳定裕度值见表1。从表1可以清晰地看到各节点的电压稳定裕度值，通过观察各点的裕度值可以发现，节点7、节点19与节点26的裕度值明显要低于其他节点。说明这3个点的电压稳定性与其他节点相比较差，因而需要对这3个点处的电压进行补偿，以确保电力系统的稳定运行。

节点7、节点19、节点26应用本文方法进行分布式电源规划后的电压稳定裕度值如图6所示。从图6可以看出，应用本文方法进行分布式电源规划后，在3个电压不稳定节点处，不同时间点测得的电压稳定裕度值和其他节点一样都保持在5左右。说明本文方法应用后可使节点电压趋于稳定，验证了本文方法的分布式电源规划有效性。

表1 各节点电压稳定裕度值Tab.1 Voltage stability margin of each node

图6 电压稳定裕度值Fig.6 Voltage stability margin

应用本文方法后某日不同信噪比下的有功网损如图7所示。

图7 不同信噪比有功网损Fig.7 Active power network loss with different SNR

从图7可以看出，随着信噪比的增加，输配电网的有功网损也随之增加，但是增加幅度不大，有功网损的值始终较低，网损最大时，也仅为约25 kW，多数情况下有功网损可维持在20 kW以下。说明应用本文方法进行分布式电源规划后配电网产生的有功网损更少，可满足实际电力工作低网损的要求。

不同投资额下应用本文改进粒子群算法和基础粒子群算法的配电网网损费用对比如图8所示。从图8可以看出，粒子群算法收敛速度较快但缺乏适当的引导，很容易早熟，得到的结果精度不高，本文改进粒子群算法在寻优过程中出现算法停滞时，通过初始化粒子跳出局部最优，使得解的精度更高，寻优效果更强，效率更高。由此表明，应用本文方法对输配电网电源进行电源规划，产生的网损费用更低，可降低输配电网的总体运营成本，可更好满足实际电力工作需求。

图8 网损费用对比Fig.8 Comparison diagram of network loss cost

应用本文改进粒子群算法得到的帕累托效率如图9所示。

图9 改进粒子群算法帕累托效率Fig.9 Improved particle swarm optimization Pareto efficiency

从图9可以看出，无论在投资费用较大或者较小的情况下，本文应用改进遗传算法得到的最优解分布都比较均匀。说明本文应用的改进粒子群算法在面对较大数据时，也具有较好的寻优能力。

4 结论

本文研究基于改进粒子群算法的输配电网分布式电源规划方法，可以显著提升输配电网能源利用率，保障电网稳定运行，满足实际电力工作中需求。但是本文在构建输配电网规划模型时考虑的因素有限，实际的输配电网电源规划中，还要受到环境等因素的影响。下一阶段对输配电网电源规划的研究，将从环境因素入手对输配电网电源进行合理有效的规划。