下击暴流作用下的开洞超高层建筑风致内压及净压
2022-08-02余先锋刘慕广谢壮宁
余先锋,赵 琦,刘慕广,谢壮宁
(华南理工大学亚热带建筑科学国家重点实验室,广东广州 510640)
下击暴流是伴随雷暴天气产生的一种近地面短时强风,一旦发生,破坏性极大,其在世界范围内已经造成大量结构物的破坏[1]。然而,相较于良态风场,对下击暴流及其与结构的作用效应研究起步较晚,主要集中于下击暴流风场特性的研究,因此有必要对下击暴流作用下的建筑结构所受风荷载效应开展深入研究。
Hjelmfelt[2]通过对大量现场实测数据进行统计分析,获得了典型下击暴流的风速剖面示意图,可见下击暴流风剖面与常规大气边界层风剖面存在明显差异。Chay 和Letchford[3-4]通过数值模拟方法研究了静态和移动下击暴流作用下的方形截面建筑表面风 压 分 布。 吉 柏 锋 和 瞿 伟 廉[5]以CAARC(commonwealth advisory aeronautical research council)高层建筑标准模型为研究对象,通过CFD方法研究揭示了下击暴流作用下高层建筑物的表面风压分布特性。Zhang[6]通过冲击射流试验装置研究发现,作用在高层建筑上的微下击暴流诱发的风荷载与传统边界层中的相应风荷载有显著差异。方智远[7]进一步采用冲击射流装置对5 种不同深宽比的高层建筑进行刚性模型测压试验,分析了深宽比和径向距离对局部和整体风荷载的影响。值得注意的是,上述研究都是针对下击暴流风场特性及其作用下的建筑外压分布特性,而对下击暴流作用下开洞高层建筑的内压特性鲜有报道。
在开洞建筑风致内压研究方面,Holmes[8]首次引入声学谐振器原理研究内压,推导出了二阶非线性的内外压传递微分方程。在此基础上,Vickery[9]、Sharma[10-11]提出了带有孔口损失系数的内压控制方程。此后,Sharma&Richards[12]建立了考虑屋盖柔度的内压控制方程;Yu[13]通过理论分析和风洞试验研究了带有背景孔隙的单空间结构风致内压响应;Yu[14]进一步推导了带有背景孔隙的两空间结构风致内压控制方程。然而,这些研究均是在良态风场作用下开展的,由于下击暴流的独特风场特性,亟待开展下击暴流作用下的开洞超高层建筑风致内压和净压研究。
文中在大气边界层风洞中通过自制发生装置来模拟下击暴流风场,并对一典型开洞高层建筑进行刚性模型同步测压试验,研究下击暴流作用下开洞高层建筑的内压和净压特性,并与常态风场下的风致内压和净压结果进行对比分析。
1 风洞试验与数据处理
1.1 试验概况
风洞试验刚性模型由3mm厚的ABS板制成,外轮廓尺寸为150mm× 150mm×900mm(长×宽×高),采用1:200 的缩尺比,用来模拟实际高度为180m的典型高层建筑。以中心高度为0.8H的上下各25mm 的楼层空间为研究对象,对应实际高度10m。在所取研究空间的一个立面中心位置设置25mm×50mm(高×宽)的开洞,在0.8H高度处布置一层测点,其中外压测点29 个,内压测点3 个,测点布置如图1所示。试验采用的风速缩尺比为1:4,为了满足内压相似准则[8],内部体积需要补偿为研究楼层空间的16倍,将研究层的上下空间作为补偿空间,模型示意图如图2所示。
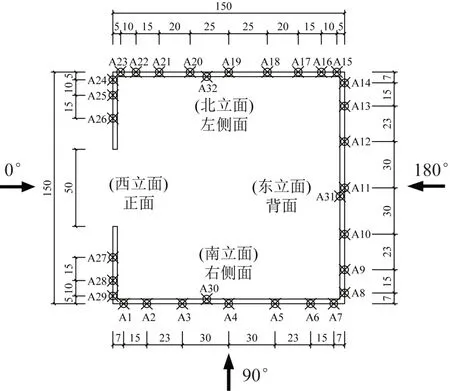
图1 测点布置(单位:mm)Fig.1 Pressure tap layout(unit:mm)
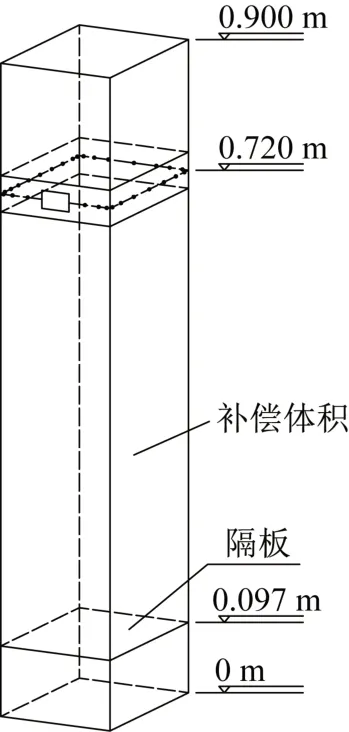
图2 风洞试验刚性模型Fig.2 Rigid model for wind tunnel experiment
模型测压试验是在华南理工大学大气边界层风洞试验室中完成的,该风洞试验段长×宽×高为24m×5.4m×3m,最高试验风速可达30 m·s-1。文中采用一种用于模拟雷暴冲击风的风洞试验装置[15]来模拟下击暴流风场。试验装置如图3 所示,该试验装置可在现有的常规大气边界层风洞内使用,加工安装方便,风场模拟结果可靠有效。

图3 下击暴流发生装置Fig.3 Downburst simulation device
文中以Vicroy 与Wood 提出的理论模型[16-17]作为下击暴流的目标风速剖面,通过调整试验装置的导流板位置、粗糙元等参数,模拟的下击暴流平均风速剖面、湍流度(Iu)分布见图4。考虑到下击暴流风场中不同径向位置的风速分布存在差异,文中选取了与上述风速剖面理论模型吻合程度最高(定义为最佳风剖面)的位置上开展试验,即试验模型与雷暴冲击风发生装置外边缘相距4.8m。
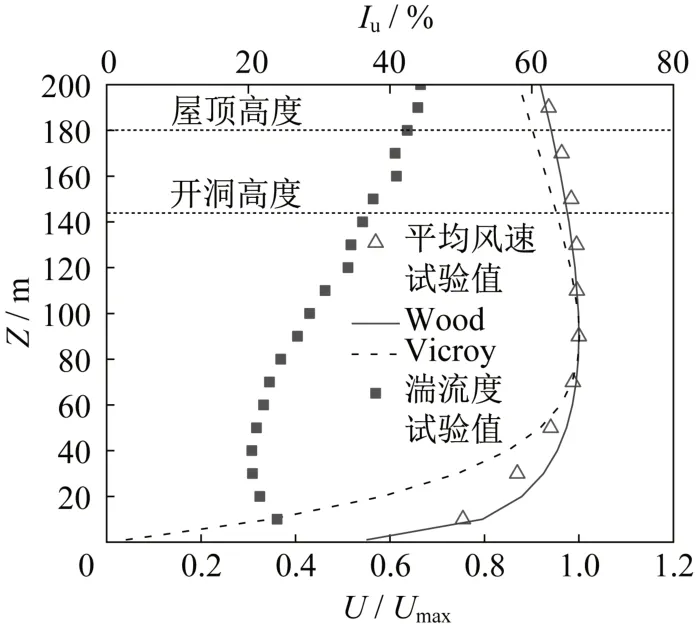
图4 模拟的下击暴流风场Fig.4 Simulated downburst wind field
为作对比,文中亦按GB50009-2012《建筑结构荷载规范》模拟了B类地貌风场,模拟出的平均风速剖面、湍流度(Iu)分布见图5。
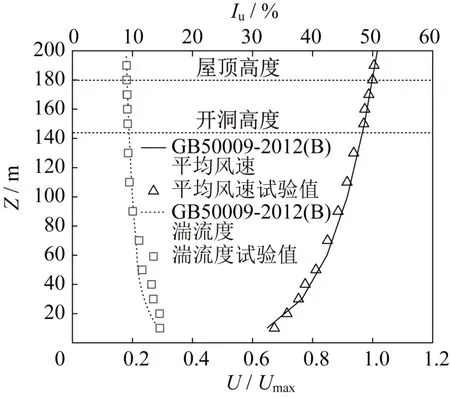
图5 模拟的B类地貌风场Fig.5 Simulated wind field in category B
考虑到结构对称性,分别在下击暴流和B 类地貌两种风场下,以10°风向为增量开展同步测压风洞试验,获得0~180°风向角下的内压和外压时程。两类风场下的试验参考高度均取为屋顶高度(H=0.9m),在H=0.9m 处的参考风速分别为Urd=8.5m·s-1(下击暴流)和Urb=10m·s-1(B类风场),风速比为1:4,试验采样频率331Hz,样本长度为20 480,采样时间共61.873s。
1.2 数据处理方法

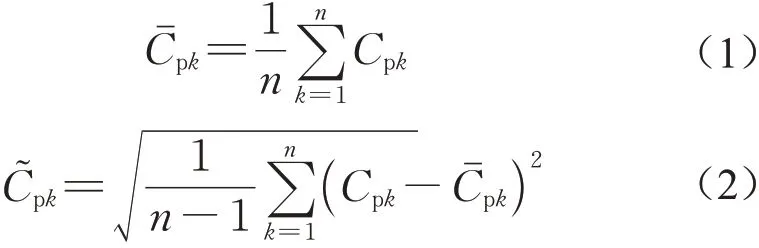
式中:n为每个测点的采样长度,本文取n=20 480。
对内压和外压测点的风压系数进行概率密度分布研究,发现部分测点并不符合高斯分布,采用Cook&Mayne[18]方法计算峰值风压系数
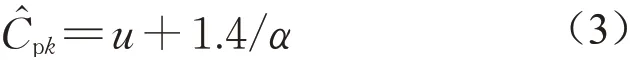
式中:u和α分别为风压系数极值分布的位置参数和尺度参数,可采用矩法计算分布参数。
进一步,净压力系数可通过以下公式计算,即
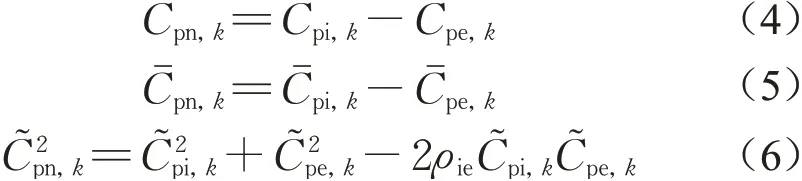
式中:Cpn,k、Cpi,k、Cpe,k分别为测点k的净压系数时程、内压系数时程和外压系数时程;ρie为内外压相关系数。面平均外压系数时程CpeA和面平均净压系数时程CpnA计算如下:
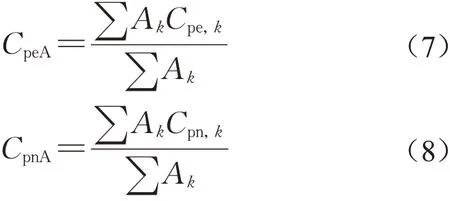
式中:Cpe,k、Cpn,k分别为某面墙上的第k个测点的外压系数时程和净压系数时程;Ak为第k个测点的有效面积。
2 试验结果分析
2.1 内压系数
由于内压在空间上完全相关[14],可取任意一个内压测点进行分析。图6为两种风场下的平均内压系数随风向角的变化,从图中可知,在各风向角下,下击暴流作用下的平均内压系数略大于B类风场的结果;两种风场下的平均内压系数均呈先减小后增大的趋势且在洞口正面迎风(0°风向附近)时平均内压系数达到最大值,在洞口侧面迎风(80°风向附近)时达到最小值。在60°~70°风向角之间由平均内压由正压变为负压,在100°~180°风向角平均内压趋于稳定。
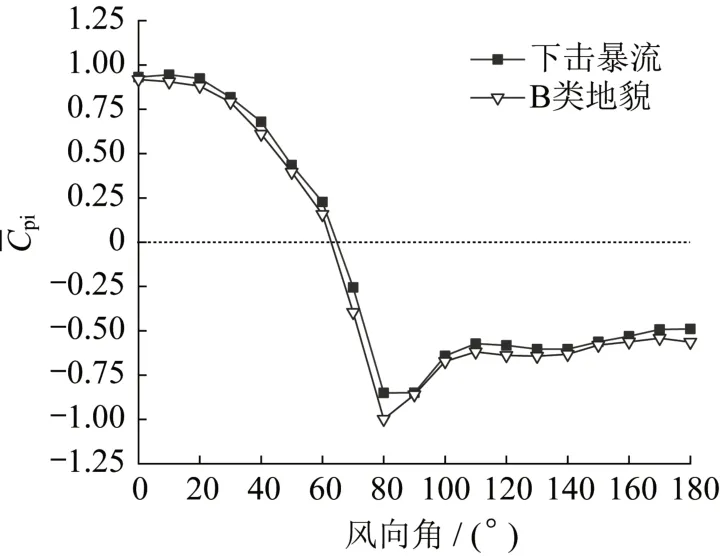
图6 下击暴流与B类风场下的Fig.6 under downburst and category B wind field
两种风场下的内压系数极值随风向角的变化见图7。由图可知,内压系数极值随风向角的变化规律与平均内压相似,也呈先减小后增大的趋势。值得注意的是,在0°~60°风向角内,下击暴流内压系数极值大于B类风场下的结果,在70°~180°风向角内,下击暴流与B类风场下的内压系数极值非常接近。图8 给出了下击暴流与B 类风场在20°、170°的内压系数功率谱密度,从图中可以看出在20°风向角下下击暴流作用下的风致内压在共振频率处的能量大于B类风场作用下的结果,而在170°风向角下两不同风场的内压系数功率谱曲线差异不大。
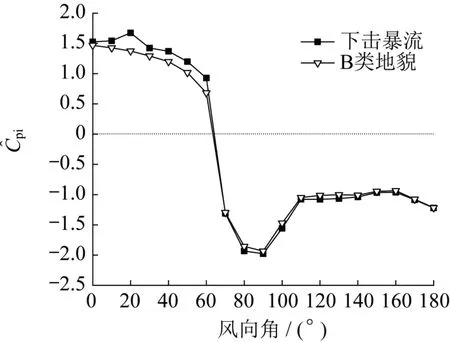
图7 下击暴流与B类风场的Fig.7 under downburst and category B wind field
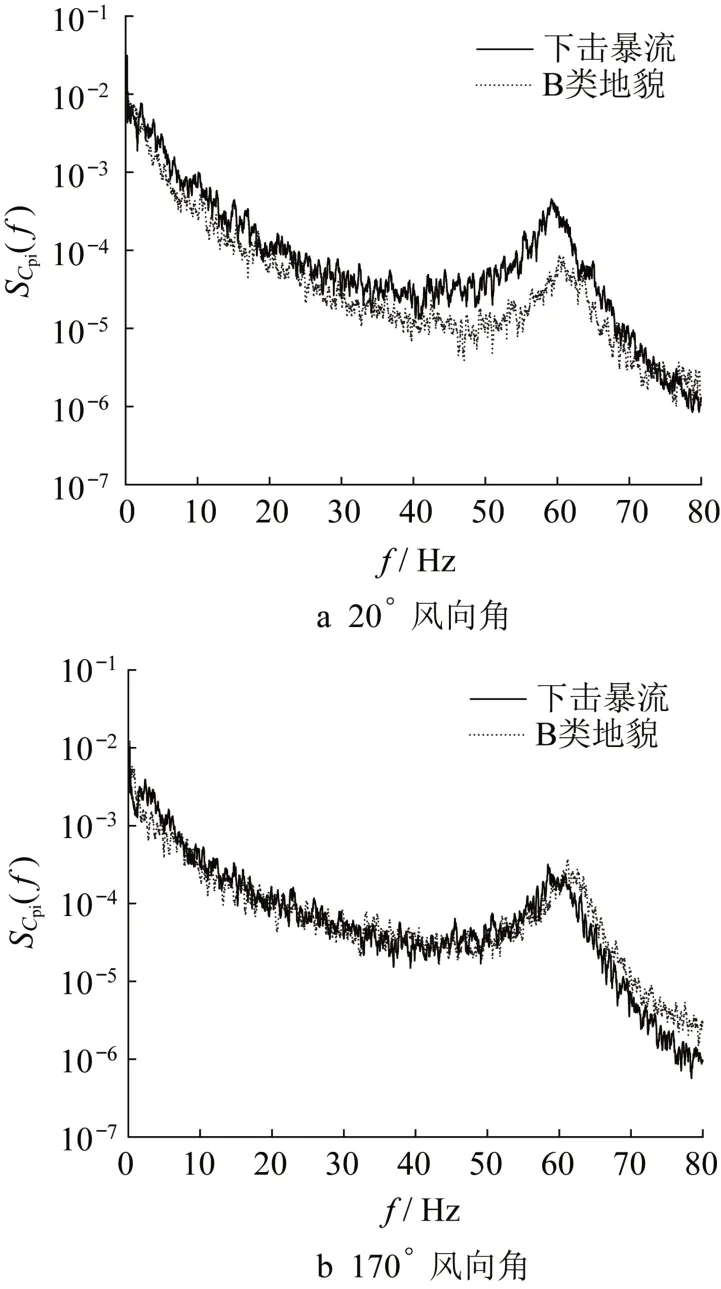
图8 内压系数功率谱密度SCpiFig.8 Power spectra of fluctuating internal pres⁃sure coefficient
2.2 净压系数
在进行围护结构的抗风设计时,起控制作用的往往是结构受到的净压极值,因此内外压联合作用的净压研究更具实际意义。图9 给出了正面、右侧面、背面、左侧面的净压系数极值随风向角的变化,由图可知,在两种风场作用下的正面(开洞面)净压系数极值在100°~170°风向范围内差异显著,而其他三个立面的净压系数极值在各个风向角下的差异都较小。
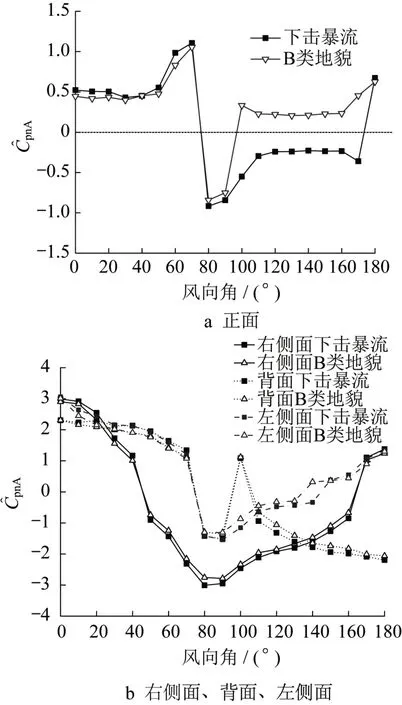
图9 面积平均净压系数极值随风向的变化Fig.9 Variation of with wind direction angle
下击暴流作用下,各立面的内外压相关系数随风向角的变化见图10。由图可知,在所有风向角下的正面内外压相关系数都为正值,内外压作用相互抵消,净压较小。右侧面的内外压相关系数在大部分角度都小于0,内外压作用相互叠加,在10°和80°风向角负相关性最强,净压系数极值分别达到了2.91和-3.01。背面内外压相关系数除了110°风向角外均小于0,内外压作用呈叠加效果,尤其是0°、90°和180°最为明显,对应的净压系数极值分别为2.31、-1.52 和-2.19。左侧面在0°风向角时内外压负相关较强,内外压作用叠加,净压系数极值达到3.06。
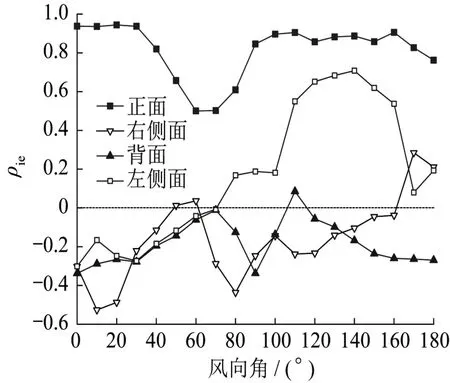
图10 下击暴流作用下各面的ρie随风向角的变化Fig.10 Variation of ρiewith wind direction angle un⁃der downburst
对比四个面的净压系数极值,右侧面、左侧面在最不利风向角时的净压极值最大,背面次之,正面(开洞面)最小。由此可见,正面(开洞面)不易风致破坏,而两侧面最易发生破坏。
2.3 内压增益
由试验获得的内压功率谱与外压功率谱可进一步求得内压增益函数。在下击暴流与B 类风场下,图11 给出了各个风向角下的Helmholtz 共振频率值,从图中可知下击暴流作用下的开洞结构Helmholtz共振频率较B类地貌结果小,其随风向角变化的波动也更小。
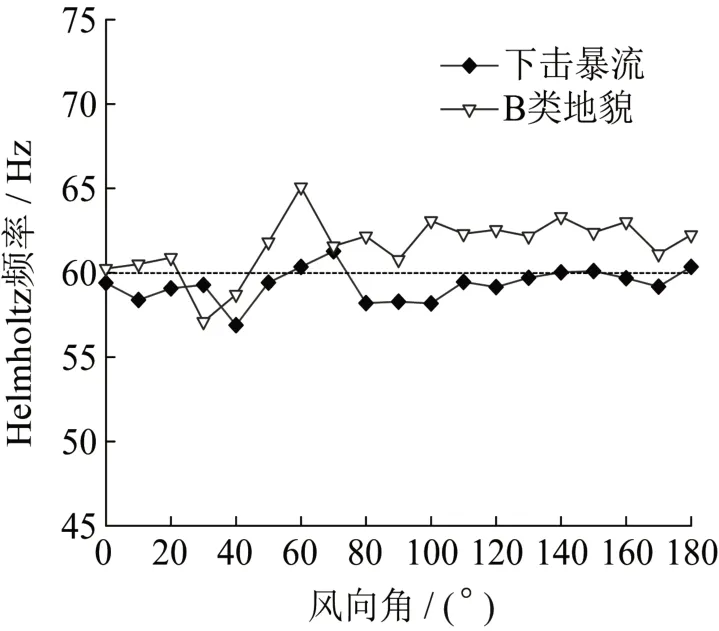
图11 Helmholtz共振频率Fig.11 Helmholtz resonant frequency
在下击暴流和B 类风场下,各个风向角下的内压增益幅值见图12,从图中可知50°风向角附近的内压增益幅值远大于其它风向角下的结果。此外在130~150°风向角时,下击暴流风场下的内压增益幅值大于B 类地貌结果。进一步,图13 给出了50°和140°风向角下的内压增益曲线,可见在50°斜风向来流作用下,在Helmholtz 频率处的内压能量显著增大,这可能是剪切流产生的旋涡脱频率与Helmholtz共振频率相近,产生了强烈的双共振所致。
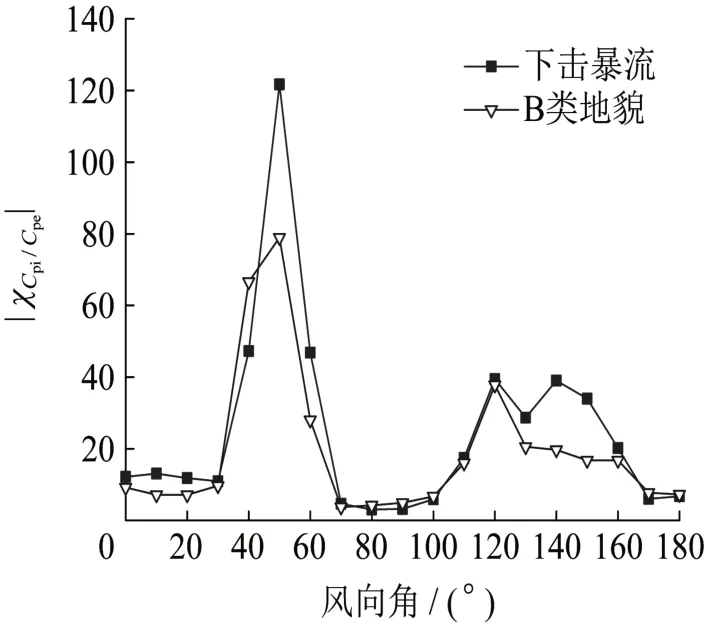
图12 内压增益幅值Fig.12 Amplitude of internal pressure gain function
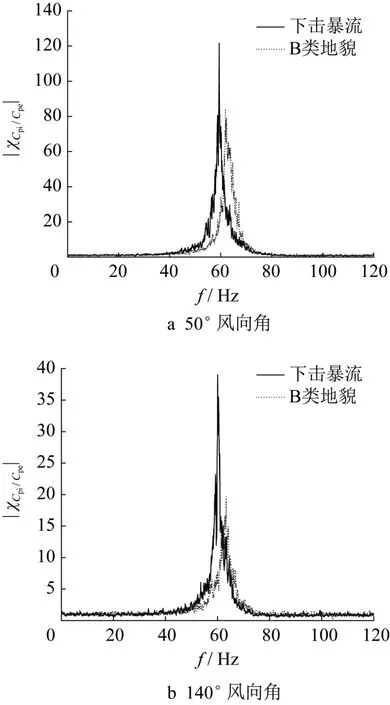
图13 内压增益曲线对比Fig.13 Comparison of internal pressure gain functions
3 与理论结果的对比分析
3.1 孔口特征参数识别
Holmes[8]首次将声学中的Helmholtz 谐振器引用到内压研究当中,推导出了二阶非线性的内外压传递微分方程。此后,学者提出了带有孔口收缩系数、孔口损失系数等不同形式的内压控制方程[9-11],其中孔口损失系数CL、孔口惯性系数CI的取值与孔口形状、大小以及来流特征等密切相关。下文根据风洞试验数据识别孔口特征参数CL、CI,并比较分析两类风场下内压理论计算值与试验值。
文中根据Sharma[10-11]提出的内传递方程进行计算,即
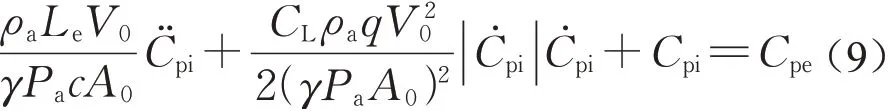
Helmholtz共振频率为
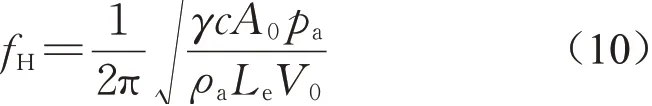
式中:空气密度ρa=1.22kg·m-3;空气比热γ=1.4;A0为开孔面积;V0为内部容积;参考高度处的风压q=0.5ρaUr2;大气压强Pa=101300Pa;孔口收缩系数c=0.6;Le为孔口气柱的有效长度,CI为孔口惯性系数;CL为孔口损失系数;Cpi、Cpe分别为内压系数和外压系数。
孔口惯性系数CI、孔口损失系数CL可据下式[19]识别获得
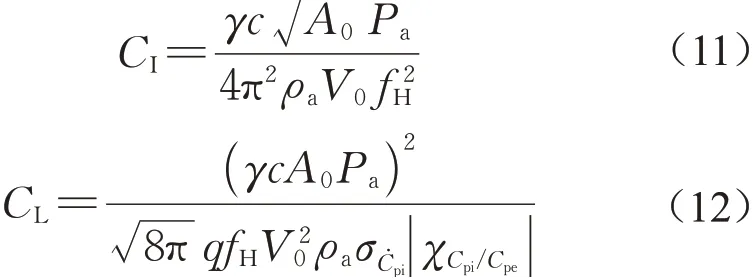
将试验得到的Helmholtz 共振频率fH代入式(11),可得孔口惯性系数CI。式(12)中σĊpi为内压系数导数的均方根,可以由试验所得的内压系数时程确定;|χCpi/Cpe|为内压增益幅值。将由试验数据求得的σĊpi和|χCpi/Cpe|代入式(12),可以计算得到孔口损失系数CL。
图14为两种风场下的孔口惯性系数CI的识别结果。
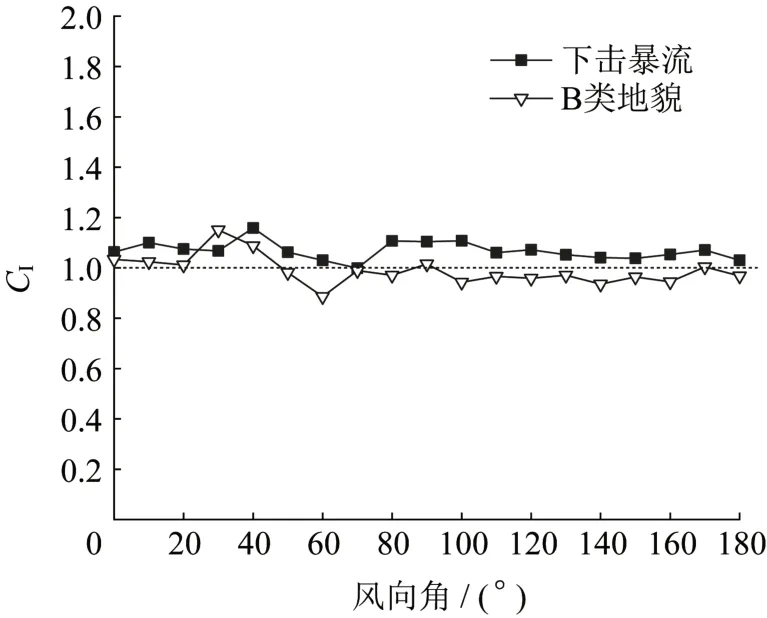
图14 孔口惯性系数CI识别结果Fig.14 Identification results of CI
各个风向角下,在下击暴流时的CI取值在1.00~1.16之间,均值为1.07,均方差为0.035;在B类风场时的CI取值在0.89~1.15 之间,均值为0.99,均方差为0.057。由此可见,孔口惯性系数CI取值较为稳定,受风向角、风场类型的影响较小。
两种风场下的孔口损失系数CL识别结果见图15。

图15 孔口损失系数CL识别结果Fig.15 Identification results of CL
从图中可以看出,CL随风向角的变化非常剧烈,但两种风场的CL随风向角的变化趋势相同,其中在0°~30°、70°~100°、170°~180°风向角的CL较大,此时两种风场下的CL也相差较大,其它风向角下的CL较小,两种风场下CL的差异也较小。
3.2 理论值与试验值对比
为了进一步验证孔口特征参数识别的准确性,将识别出的孔口特征参数代入内压控制方程进行理论计算,并将理论计算的内压系数均值、极值与试验结果进行对比分析。图16给出了下击暴流和B类风场下的内压系数极值的理论值与试验值对比。由图可知,在70°~100°风向角下,内压系数极值的理论值与试验值存在一定差异,而在其它大部分风向角下吻合良好。对于差异较大的风向角(90°),其内压系数功率谱见图17,可见在低频范围(0~25Hz)以及Helmholtz 共振频率fH处,两种风场下的内功系数功率谱理论值与试验值吻合较好,但在频率范围[25~fH]内以及大于fH的频率处,内功系数功率谱理论值与试验结果存在较大差异,其中理论功率谱值大于试验结果,这是由于孔口特征参数的识别结果在70°~100°风向角下存在差异所致。
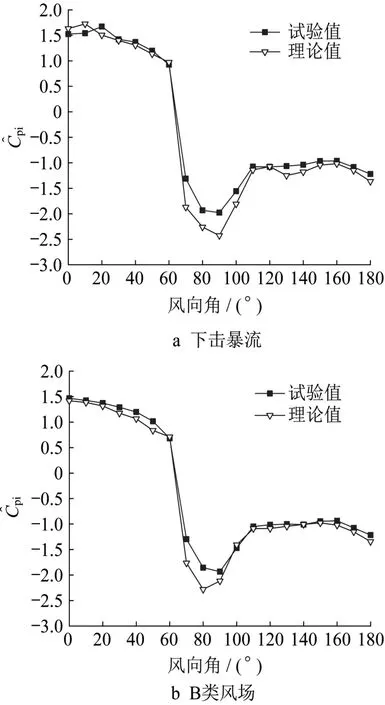
图16 的理论值与试验值对比Fig.16 Comparison between theoretical and experi⁃mental values of
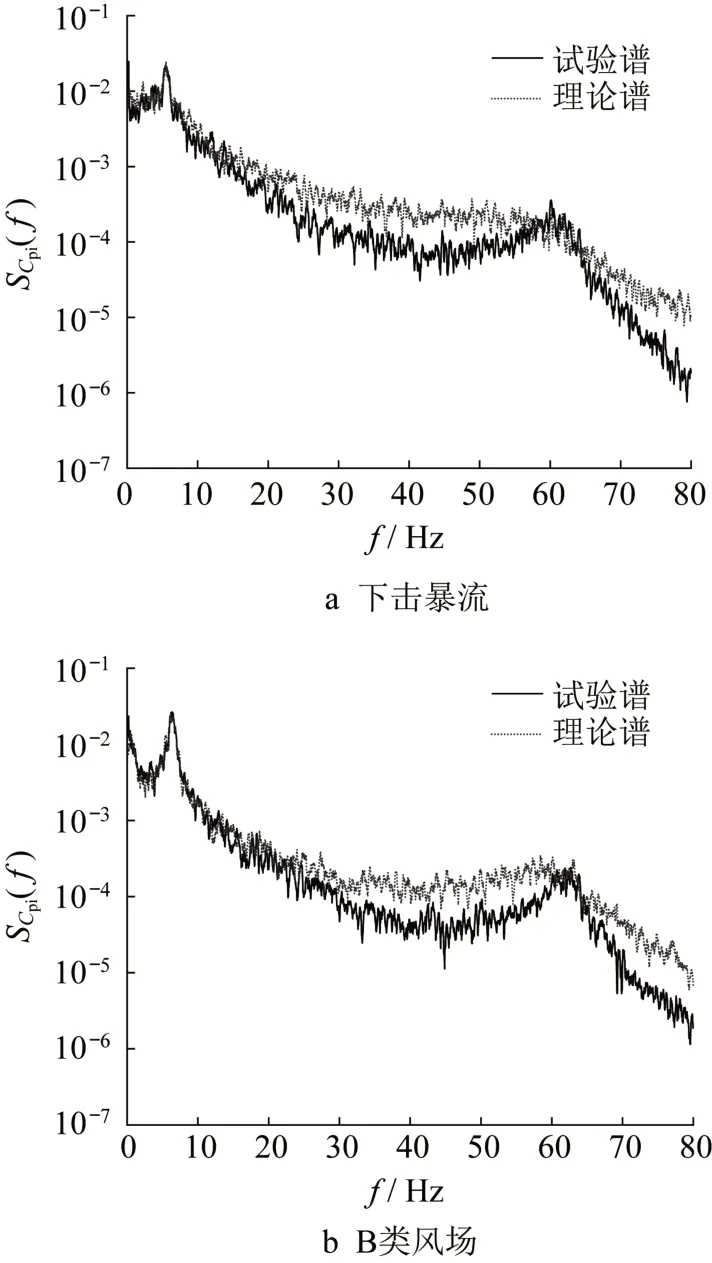
图17 内压系数功率谱SCpi的理论值与试验值对比Fig.17 Comparison between theoretical and experi⁃mental values of SCpi
4 结论
(1)内压系数极值随风向角的变化规律与平均内压相似,均呈先减小后增大的趋势。
(2)两侧面在最不利风向角时的净压极值最大,易发生风致破坏。正面(开洞面)的内外压相关系数均为正值,内外压作用相互抵消,净压最小。
(3)在50°斜风向的来流作用下,内压增益幅值远大于其它风向角下的结果,且在Helmholtz共振频率处的内压能量显著增大。
(4)孔口惯性系数CI取值较为稳定,受风向角、风场类型的影响较小,而孔口损失系数CL随风向角的变化非常剧烈,两类风场下CL随风向角的变化趋势基本相同。
(5)内压系数极值的理论值与试验值在大部分风向角下吻合良好,仅在70°~100°风向角下存在一定差异。
需要指出的是,文中仅针对位于0.8H处的开洞情况开展研究,由于两类风场在开洞高度处的差异较小,故所得两类风场下的内压系数均值和极值变化不大,但内压增益函数和孔口特征参数依然存在较大变化。实际上,开洞高度与风场剖面的相对位置对内压和净压结果有着较大影响,不同洞口高度下的内压和净压值得进一步深入研究。
作者贡献声明:
余先锋:论文的构思者及负责人,负责试验设计和论文修改。
赵琦:负责试验实施,数据分析和论文初稿写作。
刘慕广:指导试验开展,参与论文写作与绘图。
谢壮宁:负责校核试验及数据分析的结果。
