基于误差分析的火箭上浮水雷打击概率试验评定
2022-08-02叶浩亮
李 飞,叶浩亮
(中国人民解放军91388部队 92分队,广东 湛江 524022)
0 引言
火箭上浮水雷具有水深适用范围广、上浮打击速度快、作战半径大等特点,其军事经济效应好,预期的作战效能较高。打击概率是衡量火箭上浮水雷单雷作战效能的重要作战指标,其涵盖了水雷探测、识别、定位、攻击决策、上浮攻击并毁伤进入水面封锁半径内目标舰船的全过程。
打击概率作为含毁伤效果的全系统、综合性指标,其试验评定中遇到两个难题:一是无法实际使用水雷装备进行目标舰船真实打击毁伤试验;二是概率类指标考核需要大样本以提高置信度。水雷作为一次性使用武器,完全通过几十条的大样本实航试验消耗来评定从军事经济性和试验实施风险上均不可接受。因此,建立打击概率数学计算模型并利用多源实航试验数据来综合评定,是一条科学合理可行的工程化思路。
文献[1-2]建立了一种含毁伤的武器装备对目标的打击概率数学模型,综合考虑了瞄准误差和正横距离估计误差,并将舰船目标毁伤平面等效为矩形,但其存在几个问题:1)未考虑水雷对目标舰船的动作概率,即给出攻击指令的概率;2)未考虑火箭上浮弹道的系统误差,并将火箭上浮弹道二维两向散布误差等同;3)将水雷的预测打击点误差简单的用正横误差来代替;4)未考虑火箭上浮水雷主动攻击时舰船等效毁伤面积的计算。文献[3-6]建立了区域攻击火箭上浮水雷的命中概率计算模型,但其均是从水雷固定区域攻击的角度来计算命中概率,与在封锁半径内任意点打击目标的火箭上浮水雷作战方式不符;另外其也未考虑水雷对目标舰船的动作概率、综合打击概率、毁伤效果以及试验评定工程化实施过程中的样本量分配和测量误差修正等因素。
本文通过分析火箭上浮水雷的工作原理以及攻击毁伤目标的全过程,结合误差分析和武器系统单发命中理论,综合考虑火箭上浮水雷的动作概率、预测打击点误差、火箭上浮弹道散布误差、水雷水下爆炸毁伤半径和目标舰船等效毁伤区域、试验评定工程化实施中的测量误差修正、试验样本量分配等因素,建立了一套可实际工程应用的打击概率试验评定模型,其不仅可用于评定火箭上浮水雷的打击概率,同时可扩展到其他水雷如沉底雷等装备的打击概率评定中。
1 火箭上浮水雷打击成功判别标准
1.1 水雷的水下毁伤半径计算
火箭上浮水雷的打击概率定义为:目标舰船从封锁半径内通过时,水雷上浮攻击并按规定的毁伤效果毁伤目标舰船的概率。一次有效的打击毁伤目标过程火箭上浮水雷要完成以下动作:
1)水雷正确探测到目标,并完成识别、定位;之后依据水深、火箭上浮速度和弹道等计算出上浮打击时间,结合目标运动要素,给出打击目标的提前点,即预测攻击点;
2)水雷向预测攻击点上浮攻击,并在预定起爆深度起爆毁伤目标。
图1是火箭水雷上浮攻击、毁伤目标过程的示意图。

图1 火箭上浮水雷攻击毁伤目标示意图
水雷的毁伤效果一般采用冲击因子体系描述[7-9],其是英国、意大利以及北约许多国家共同采用的舰船破坏标准,用以评定水中兵器毁伤水面舰艇的能力。冲击因子破坏标准有计算简单的特点,而且可以根据对舰船毁伤程度的要求方便地将其换算为概率值,较适合于水雷类中远距离非接触爆炸的水中兵器;不足之处是没有考虑舰船结构特征影响。
使用冲击因子描述水雷毁伤效果时,可用水下毁伤半径来表征水雷按规定毁伤效果毁伤舰船时的空间范围,即:
(1)
式(1)中,k1为炸药的TNT当量系数;k2为海底反射系数;G为炸药的质量;R为水下毁伤半径;SF为冲击因子;α为爆心距水面舰船龙骨中心连线与水平方向的夹角(具体见图1)。火箭上浮水雷起爆时均远离海底,因此海底反射系数k2取1;在水雷装药G、炸药的TNT当量系数k1、冲击因子SF已知的情况下,式(1)可等价为:
(2)

试验中,获取水雷爆点B的位置以及起爆时刻舰船的真实位置,并据此计算出爆点距舰船底部中线段最近距离Rx,将舰船吃水深度h、起爆点深度h1代入式(2),计算出水下毁伤半径R,若Rx≤R,则水雷打击毁伤成功;反之,水雷打击毁伤失败。
1.2 水雷有效毁伤区域的水面投影半径
火箭上浮水雷的爆点深度h一般是固定值,因此爆点只能在深度h的平面内散布。如图2所示,爆点在B0、B1和B2连线上散布,每处爆点皆有一个对应的水下毁伤半径。
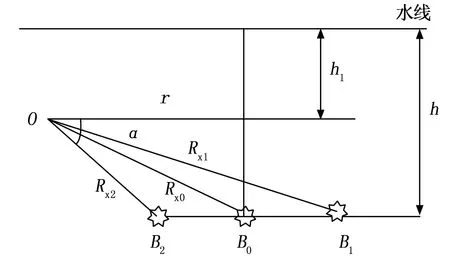
图2 有效毁伤区域的水面投影半径
假设在B0处爆点距舰船底部中线的距离等于水下毁伤半径,代入式(2),可解一元二次方程得一个固定水下毁伤半径R0=Rx0。此时,依据式(2)的计算关系,在B2处爆点舰船中线的距离Rx2将小于此处的水下毁伤半径,水雷攻击成功;反之,爆点在B1处将攻击失败。
可见,对于爆点深度固定的火箭上浮水雷,其存在一个固定的水下位置,为水雷打击毁伤成功的判别线。反映到图2中,爆点只有落在平面投影半径r的范围内才能有效毁伤目标,r为有效毁伤区域的水面投影半径,其起点为舰船底部中线段。
(3)
2 火箭上浮水雷打击概率建模计算
2.1 打击概率总体计算模型
将火箭上浮水雷对目标的探测、识别、定位、攻击决策、下发目标参数和攻击指令这一过程效果用动作概率Patk来表征,将水雷上浮攻击、起爆及毁伤目标效果用命中概率来Phit表征,则火箭上浮水雷的打击概率PSTK可表示为:
PSTK=PatkPhit
(4)
动作概率Patk可通过水雷目标探测系统动作区域性试验获得大量的样本,试验实施相对简单;命中概率的Phit则需要综合考虑预测攻击点误差、火箭上浮弹道误差、爆点深度、水雷装药量和爆炸威力、目标舰船吃水深度和水线下轮廓形状等一系列因素,需要建模计算。
图2中,爆点位置在水平面上的二维位置只要在有效毁伤区域水面投影半径r之内,就可保证爆点距舰船距离小于毁伤半径。建立爆点水平位置散布的概率分布模型,并在有效毁伤区域AT内积分,即可计算出命中概率Phit。
Phit=∬ATψ(x,φ)dxdφ
(5)
式(5)中,ψ(x,φ)为爆点在水平面上的误差散布概率密度函数。
2.2 目标舰船等效毁伤区域AT的确定
由于水下毁伤半径的存在,水雷水下爆炸毁伤舰船时,会存在一个明显的等效毁伤区域,如图2中所示。由于毁伤半径计算起点为舰船中线,而不同的舰船类型水线处宽度不一致,因此存在与水面毁伤半径对比的关系。主要有以下两类。
1)r大于等于舰船水线半宽的情况:
图3(a)为舰船水线处形状,图3(b)为r大于等于舰船水线半宽时,目标舰船命中概率积分计算时的等效毁伤区域AT。

图3 r大于等于舰船水线半宽时的等效毁伤区域
2)r小于舰船水线半宽的情况:
当舰船水线半宽大于有效毁伤区域的水面投影半径时,有效毁伤区域在舰船宽向是舰船的实际水线宽。如图4(a)所示。一般这种情况出现在船体宽度很大的大型货轮上,可将其水线处甲板面近似看成椭圆面,则其面积可等效为长0.8Lj、宽Bj的矩形[13],如图4(a)所示,水线甲板等效面积A如下:
(6)
其有效毁伤区域AT如图4(b)所示。
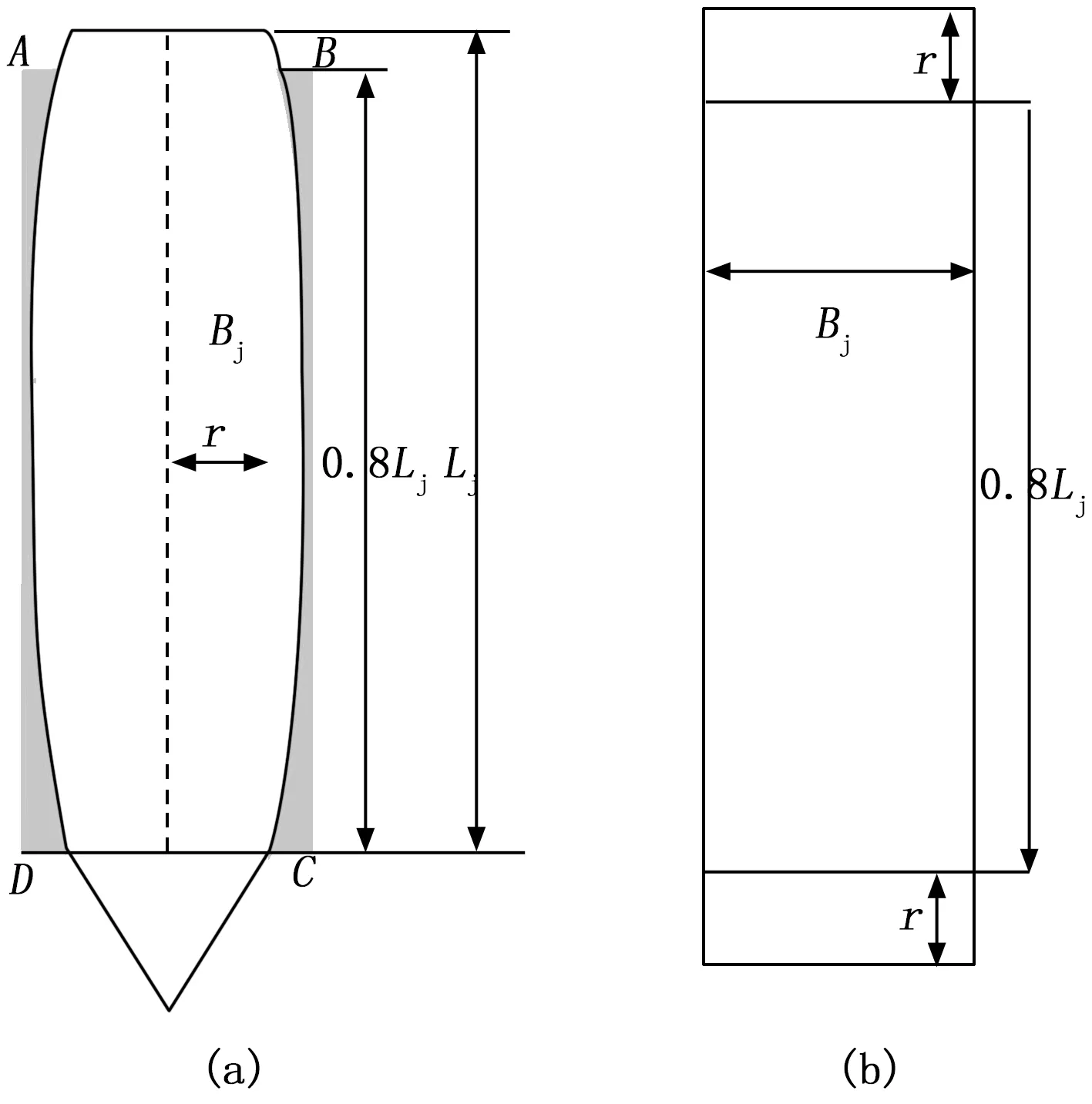
图4 r小于舰船水线半宽时的等效毁伤区域
2.3 爆点误差散布分析及建模计算
严格来说,火箭上浮攻击水雷的爆点散布是一个与爆点深度控制误差、预测攻击点误差和上浮弹道散布误差相关的三维函数。建立爆点误差散布函数需考虑起爆深度h的控制误差。目前传感器及控制技术的发展水平可将起爆深度h的误差范围控制在5 m以内,假设起爆点深度控制误差为一随机误差且服从N(0,σ)的正态分布,按照3σ原则,爆点深度误差的标准差在2 m以内,相对于预测攻击点和上浮弹道散布误差,工程应用上可将此误差可忽略不计。
依据随机误差传递和合成理论,假设水雷的预测攻击点误差、上浮弹道散布误差传递合成为最终的攻击命中误差,该误差在舰船航行向和正横距离向服从二维正态分布,则有:
ψ(x,φ)=
(7)
式(7)中,K为协方差矩阵,M为均值矩阵。
(8)
建立起爆时刻目标舰船坐标系,坐标原点为舰船中心点,舰船航行向为E轴,正横距离向为N轴,则攻击命中误差分解合成关系见图5,图6为爆点散布误差水面二维投影示意图。
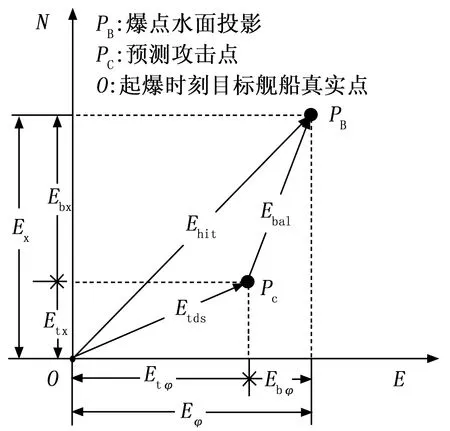
图5 爆点散布误差分解图

图6 爆点散布误差水面二维投影示意图
图5中,攻击命中的爆点误差Ehit由两部分误差合成:
1)预测攻击点的误差Etds,其由水雷的目标探测系统产生,其在正横距离向和舰船航行向的分量为Etx和Etφ;
2)上浮弹道散布误差Ebal,其在正横距离向和舰船航行向的投影为Ebx和Ebφ。
上述所有的误差均为随机概率误差,可用其标准差代替。
根据误差传递和合成理论[14-15],若随机变量x、y、z有如下关系:
y=f(x,z)
(9)
Δx、Δy、Δz分别为x、y、z的随机误差,且Δx和Δz为独立观测的量,则有:
(10)
μx、μy、μz分别为x、y、z的系统误差,则有:
(11)
对于火箭上浮水雷,一般由目标探测系统和战斗载荷系统分别负责目标探测识别定位和上浮攻击起爆,两个系统之间一般是相互独立的,因此Etds和Ebal相互独立,其随机误差传递为代数和关系,综合以上有:
(12)
(13)
由此,计算命中概率所需的所有变量均已明确,可综合式(7)、式(5),在试验中通过大样本获取预测攻击点误差的均值和标准差、上浮弹道散布误差的均值和标准差后,计算打击概率。
3 打击概率试验评定方案
3.1 试验方案设计约束分析
武器装备试验方案设计是一个需要在多种、多重约束限制条件下将理论方案工程化、可实施化的过程[16]。章节2虽建立了打击概率的计算模型,但在其工程化过程中,仍需要考虑诸多影响和限制因素。结合实际情况,主要考虑以下问题。
1)试验数据的正态分布检验:
火箭上浮水雷打击概率建模计算的核心为误差分析和正态分布假设。在中心极限定理框架下,大量试验样本可保证正态分布假设的合理性;但实际试验中考虑到样机消耗,火箭上浮弹道散布误差样本一般不超过20个。此时,在应用打击概率计算模型前,必须对相关数据进行一次正态分布检验,如Shapiro-Wilk检验等,以保证建模计算前提的符合性。
2)数据测量误差的分析处理:
实际试验中,预测攻击点误差、上浮弹道散布误差的获取均依赖水雷水下雷位、目标舰船航迹数据。目标舰船的航迹由GPS获取,水雷水下雷位一般由超短基线等水声定位方式获取。两种测量方式均存在测量误差,尤其水雷雷位的水声定位误差,基本在10~15 m左右,对于精准攻击的火箭上浮水雷,该误差在数量级上显然已与预测攻击点误差相近,不进行分析处理将严重影响计算结果。
3)不同目标舰船和正横距离的样本分配:
不同类型舰船的外形特征及噪声水平不同,通过雷区时正横距离不同,导致水雷打击时对其的探测识别和定位水平不同、等效毁伤区域不同、上浮弹道攻击时间也不同。也即是:不同打击目标态势下,预测攻击点和上浮弹道散布误差虽均服从同一分布,但其均值和标准差可能完全不一致,章节3的打击概率模型单次只能算一种特定攻击态势下的打击概率。
作为综合性、系统性指标,打击概率是表征水雷打击在封锁半径范围内目标整体的平均水平,因此设计试验方案时,必须考虑多型目标和多种正横距离的样本分配,在兼顾计算打击概率样本最小需求前提下,涵盖尽量多的目标舰船类型和正横距离。
3.2 具体试验评定方案
1)动作概率Patk的试验方案:
在水雷目标探测系统动作区域性试验中,充分进行多型目标舰船的动作概率Patk摸底;同时为保证封锁区域的覆盖性,尽量在正横距离的边界处获得试验样本,以边界试验样本代替不同正横距离内的普通样本。
2)命中概率Phit的试验方案:
水下火箭上浮弹道散布误差只与弹道行程也即攻击正横距离相关,与目标舰船类型、航速航向等均无关,因此只需在边界正横距离处获取上浮弹道散布误差样本即可,以边界试验样本代替不同正横距离内的普通样本。
3)打击概率PSTK的综合计算:
假设试验中共进行了n型不同的目标舰船打击概率试验,每型目标舰船的打击概率为Pstki,依据事前侦查情报或者单独的界定,在未来战场上每型目标舰船通过水雷封锁区域的概率权重为wi,则该型水雷的打击概率可表述为:
(14)
4)测量误差的修正方案:
由GPS和水声定位带来的测量误差主要影响水雷预测攻击点误差的计算。火箭上浮弹道散布误差一般通过内置的高精度惯组测量位移量实现,与外界的定位测量无关。GPS和水声定位测量误差为随机误差,一般可将其视作服从均值为0的二维正态分布。以Egps和Eapa分别代表GPS和水声定位误差,其标准差分别为σgps和σapa;以M0表示水雷雷位真值,s0表示预测攻击时刻舰船位置真值,EPR表示水雷计算出的预测攻击点相对雷位的位置,则由含误差的试验数据获取的预测攻击点位置Pc为:
Pc=(M0+Eapa)+EPR
(15)
由含误差的试验数据获取的预测攻击时刻舰船位置sc为:
sc=s0+EGPS
(16)
由试验数据获取的预测攻击点误差为:
Etdsc=pc-sc=(M0+EPR-s0)+(Eapa-Egps)=
Etds+(Eapa-Egps)
(17)
可见,测量误差在数据处理过程中,是以简单的代数运算叠加在处理结果中的。作为均值为0的随机误差,可通过误差传递定理来进行修正。
令由含误差的试验数据计算出的预测攻击点标准差为σtc,标准差的真值为σtds,则有:
(18)
σgps和σapa可由具体测量设备的性能指标得到。
4 典型算例及分析
假设某型火箭上浮水雷装药量为400 kg(TNT当量);起爆深度设计值为20±5 m;打击目标舰船主要分为三大类:典型驱护舰、典型军辅船以及大型目标舰船,三型舰船典型吃水深度及尺寸、有效毁伤区域水面投影半径如表1所示。
表2中,假设了一组水雷对不同目标舰船的动作概率、预测攻击点和上浮弹道散布误差数据,并依据表1中目标舰船的尺寸信息及有效毁伤区域水面投影半径,计算出了对应的打击概率。
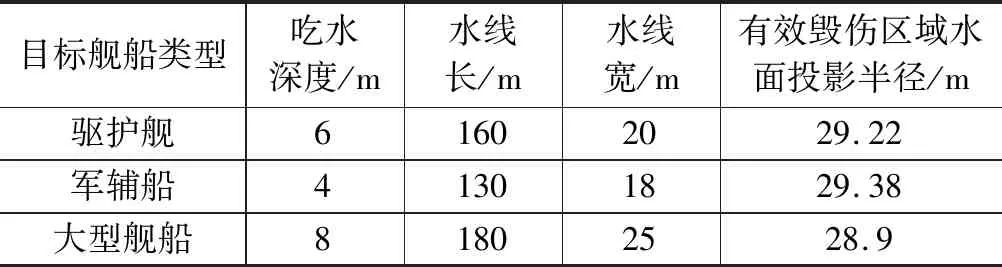
表1 典型目标舰船尺寸信息及对应的毁伤半径

表2 打击概率计算案例
由表1可看出,按照冲击因子体系描述舰船毁伤效果时,一般水面舰船的水线半宽均小于其对应的有效毁伤区域水面投影半径;此时,等效毁伤区域主要参照图3。
一般水面舰船的水线长远大于水线宽。综合表1和表2可看出,计算命中概率时,等效毁伤区域的二维面积分中,水线长向积分很容易达到高概率。反映到实际打击场景中,目标舰船的水线长基本相当于水雷的封锁半径,此时水雷攻击在水线长向很容易上靶;目标舰船的水线宽向相对较小,攻击时上靶较水线长向难度大。因此,影响火箭上浮水雷打击概率的主要因素是水线宽向的预测攻击点精度,在水雷研制设计时应重点关注该方面的性能指标实现。
水雷在研制设计时,受限于空间尺寸,一般装药质量很难大范围变动,而起爆深度则可在控制系统中较容易调整。假设水雷装药量为400 kg(TNT当量),其起爆深度可在12~30 m内变动,在目标舰船吃水深度固定(表1中典型驱护舰吃水深度6 m)的情况下,计算不同起爆深度下的有效毁伤区域水面投影半径,结果如图7所示。
由图7可看出,装药量和目标舰船吃水深度固定的情况下,存在一个最佳的起爆深度,使有效毁伤区域水面投影半径最大,此时命中概率最大。因此,水雷在研制设计时,应根据打击目标舰船的实际尺寸、装药质量来合理选择最佳起爆深度,以达到最佳的打击概率。

图7 装药量和目标舰船吃水深度固定情况下不同起爆深度的有效毁伤区域水面投影半径
5 结束语
本文在分析火箭上浮水雷探测、识别、定位、上浮打击目标的全过程的基础上,结合水下非接触爆炸毁伤原理,综合利用误差分析和数理统计方法建立了一套火箭上浮水雷打击概率计算模型;之后在解决试验评定工程化实施过程中的测量误差修正和样本量分配等问题的基础上,提出了一套可实际工程化应用的火箭上浮水雷打击概率试验评定方案。该方案解决了封锁区域内任意点攻击的火箭上浮水雷打击概率考核问题,且已成功应用至某型火箭上浮水雷的性能鉴定试验和作战效能评估中。典型计算案例表明,该方案在保证试验评定质量的同时可大幅提高试验实施质效,不仅可推广应用至其他类型水雷(如沉底雷)的打击概率试验评定中,还可在一定程度上指导火箭上浮水雷的设计和研制。
