基于铜球测压法的压力波影响规律研究*

刘 琦 王育维 郭映华 朱文芳

（西北机电工程研究所 咸阳 712099）

1 引言

随着火炮性能及内弹道与装药性能的不断提高，火炮发射过程中会出现内弹道环境异常现象，主要表现是火炮发射过程中存在膛压曲线不光滑的现象，甚至出现膛压的强烈波动［1］。典型强烈波动的膛压曲线与正常膛压曲线的对比见图1。

随着火炮武器系统作战任务的多样化，需在同一火炮平台条件下实现多弹种兼容发射。如果压力波动超过一定程度，作用在弹丸上的压力（过载）将不会是连续、均匀的，必然带来动态条件下重复加载过程，甚至超出电子控制部件抗过载能力，造成发射失败［2～3］。

本文根据大口径火炮常用的铜球测压方法，仿真计算铜球测压器在不同膛内压力曲线下的作用结果，对所建立的瞬态动力学模型进行验证，在此基础上，对比某大口径火炮弹丸在不同膛内瞬态压力条件下（有、无压力波）受力过程进行对比分析，为制导炮弹强度设计及火炮弹、炮、药耦合设计提供技术基础。

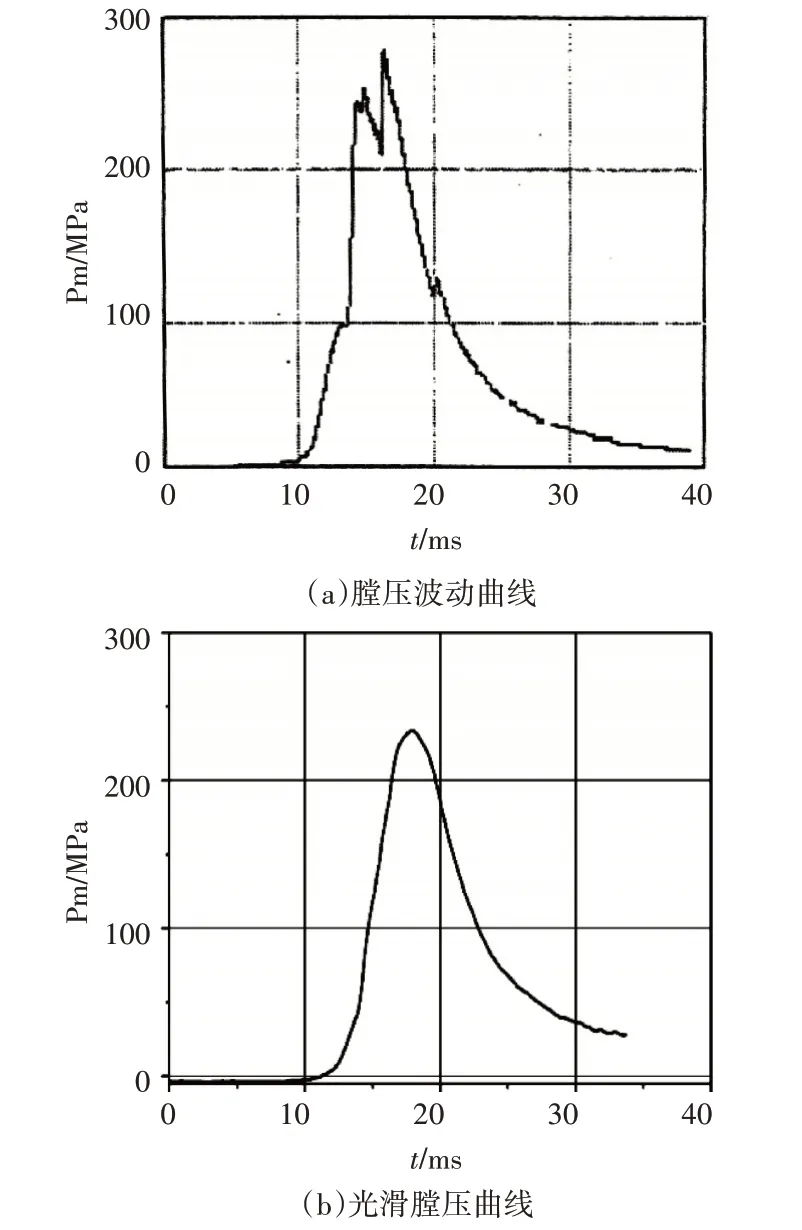
图1 某大口径火炮膛内强烈压力波动膛压曲线与正常光滑膛压曲线对比

2 压力波对铜球测压结果的影响规律研究

2.1 铜球测压器

按照GJB2773-96 规定，一般铜球测压器用来测试火炮膛内最大压力值。按照此规定，一般大口径火炮铜球测压器铜球规格参数为S ∅4.763，撞杆直径：∅3.70mm，标定温度：20℃［4～5］。表1规定了我国典型火炮装药交验用测压器材校准方法，本文根据某大口径加榴炮所需的测压范围，选择∅4.763mm铜球测压器作为分析对象［6～7］。

2.2 几何模型

根据GJB2773-96 规定，铜球测压器的规格按表1进行选择［8］。本文根据某大口径火炮小号装药某次靶场试验的测压结果，对本文所建立的动力学模型进行验证。某大口径火炮小号装药典型的压力曲线如图2 所示。根据表1 规定，本模型选择的铜球规格为∅4.763mm，活塞体积为14.5cm3，测压范围为100MPa～500MPa［9～10］。几何模型如图3所示。

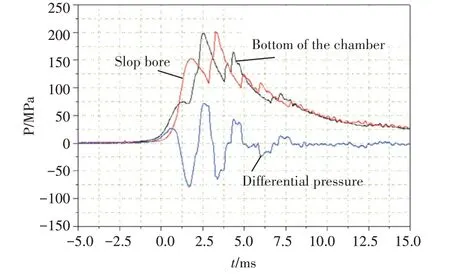
图2 某大口径火炮小号装药膛压曲线

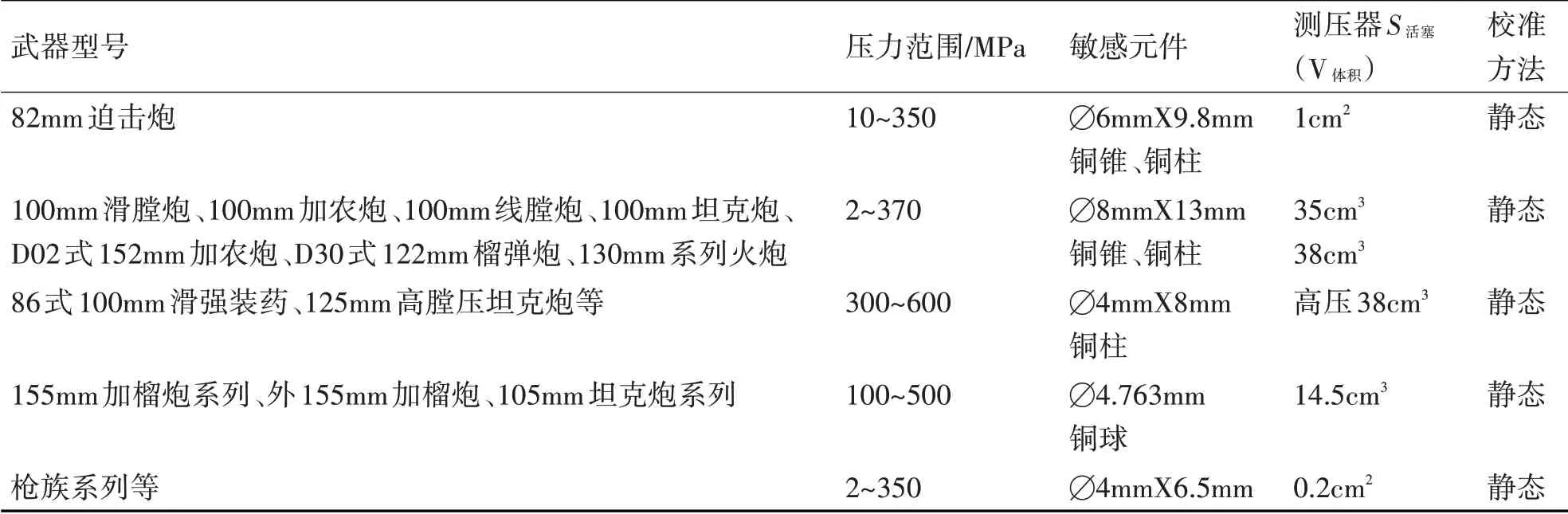
表1 我国典型火炮装药交验用测压器材及校准方法

2.3 有限元模型及材料属性

由于铜球测压器模型较简单，为了保证计算结果的准确性，网格划分采用比较小的单元尺寸，单元大小为0.1mm，选择自动网格划分方式，最终划分的有限元模型节点数为18 万，单元数为6.6 万，如图4所示。模型中测压铜球的材料参数如表2所示，活塞体与砧板的材料设置为结构钢。

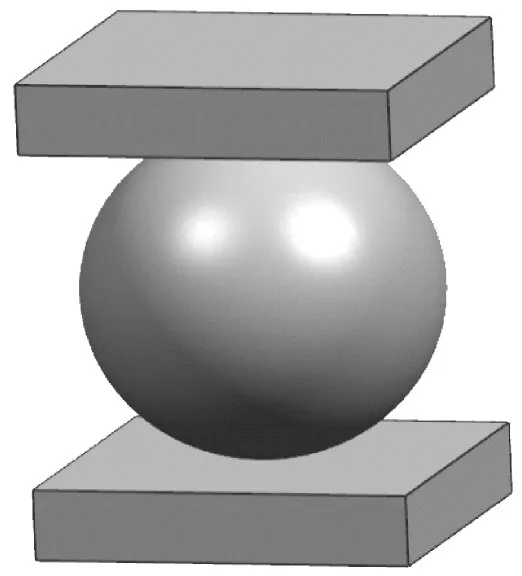
图3 铜球测压器简化模型∅4.763mm

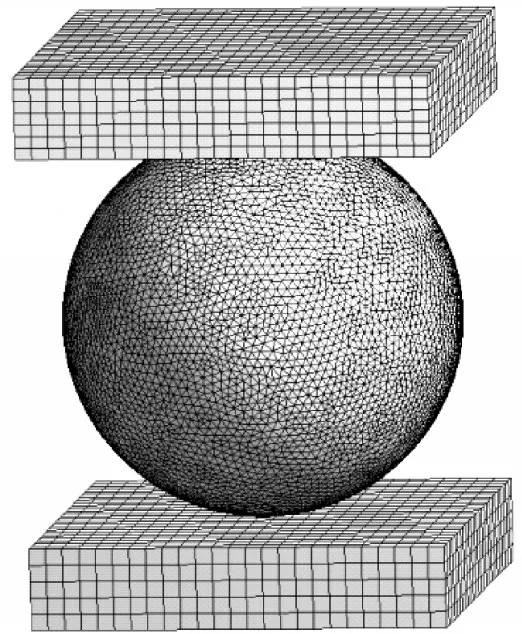
图4 铜球测压器有限单元模型

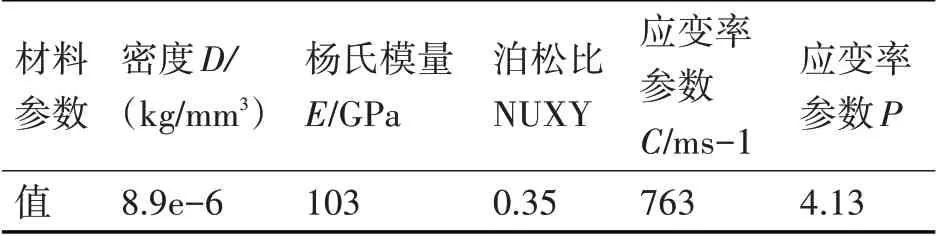
表2 测压铜球材料参数

2.4 结果分析

对上节铜球测压器系统有限元模型设置材料参数，给定使用环境下的边界条件：1）砧板底端面加载固定约束；2）活塞上表面加载图3 所示的瞬态变化的膛压；3）其它自由度不受限制，得到膛内压力峰值时刻铜柱的应力云图如图5 及卸载后铜柱的轴向变形量如图6。

图5 膛内峰值压力时刻铜球应力云图

在相同的边界条件下，将仿真计算得出的峰值相同的单峰膛压曲线加载到铜球测压器活塞上表面，得出膛内压力峰值时刻铜球应力云图如图7 及卸载后铜球的塑性变形量如图8。

图6 膛压卸载后铜球塑性变形

图7 压力峰值时刻铜球应力云图

图8 卸载后铜球塑性变形云图

将两种瞬态压力作用下铜球变形结果与铜球测压器准动态标定试验数据做对比，结果如表3。

从表3 看出，铜球测压器在同样峰值的瞬态压力加载作用下，膛内存在压力波动时，最大应力值增大约27.2%，塑性变形量增大约14.3%，而实测铜球测压器在图3 所示膛内瞬态压力作用下的变形量为0.9502mm，与表3铜球测压器实测结果相对误差为3.24%（231.1MPa），证明所建立的铜球测压器膛内瞬态压力作用下的动力学模型具有较高的准确性。

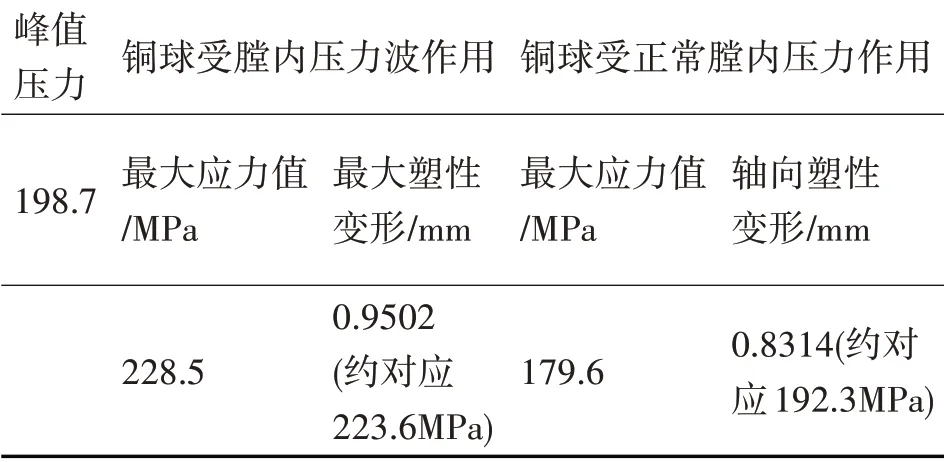
表3 两种瞬态压力加载作用下铜球塑性变形量与准动态标定结果对比

3 膛内瞬态压力对弹丸的影响规律研究

上节验证了本文所建立的膛内瞬态压力作用下的动力学模型具有较高的准确性，在此基础上，本文进一步研究了某大口径火炮弹丸在膛内瞬态压力作用下的受力情况，为制导炮弹的强度设计及系统考虑弹、炮、药的耦合设计提供参考。

3.1 几何模型及有限元模型

按照某大口径火炮身管及弹丸的实际结构，建立其身管与弹丸几何模型，如图9所示。

图9 几何模型

图10 有限元模型

应用动力学分析软件建立有限元模型，身管、弹体、弹带不刻槽部分采用Solid164 六面体拉格朗日单元进行网格划分，并对膛线起始部进行了局部网格加密［11～12］。弹带刻槽部分采用无网格光滑粒子流体动力（SPH）算法进行计算，最终的耦合有限元模型如图10。

3.2 材料参数

本文模型中弹体材料为合金钢，身管材料为炮钢，在本次模拟中均采用弹塑性本构模型，材料参数如表4［13～14］。弹带材料为紫铜，计算中采用Johnson-Cook模型参数。

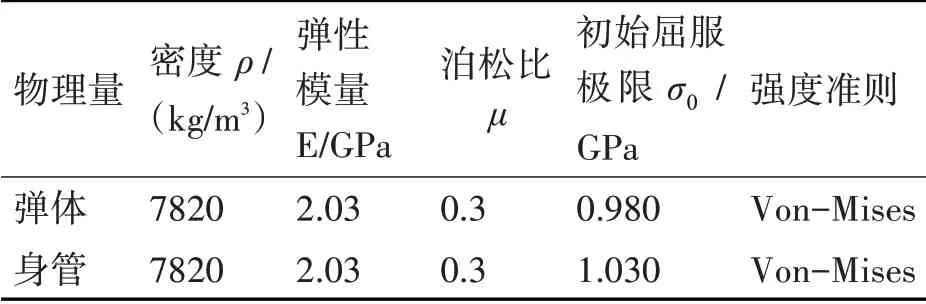
表4 弹体及身管材料参数

3.3 计算结果对比分析

图11 弹丸在膛内压力曲线下的峰值应力云图

分别将图2 的膛内实测瞬态压力曲线及内弹道计算所得到的相同峰值的单峰膛内压力曲线作用于弹底，计算得到弹丸速炮口初速（461.2m∕s）与实测炮口初速（473.1m∕s）相对误差为2.52%，证明所建立的火炮发射过程耦合动力学模型较准确。而在两种膛内瞬态压力作用下，弹丸在膛内峰值压力时刻的应力云图见图11，弹体最大应力分别为655MPa 和562MPa。可见，弹丸最大应力在压力波作用下比单峰瞬态压力作用下增加约16.5%，这对制导炮弹的发射环境是不利的。

4 结语

本文根据大口径火炮常用的铜球测压方法，建立铜球测压器系统在不同膛内压力曲线下的作用结果，对所建立的瞬态动力学模型进行验证，在此基础上，对比某大口径火炮弹丸在不同膛内瞬态压力条件下（有无压力波）受力过程进行对比分析，结果表明：

1）铜球测压器在实测某小号装药膛内瞬态压力作用下的膛底测压结果为231.1MPa，与仿真计算所得结果相对误差为3.24%，证明所建立的膛内瞬态压力作用下的铜球测压系统动力学模型具有较高的准确性。

2）铜球测压器在某小号装药条件下，在同样峰值的瞬态压力加载作用下，膛内存在压力波动时，最大应力值增大约27.2%，塑性变形量增大约14.3%。

3）在某小号装药条件下，弹体在压力波作用下及单峰瞬态压力作用下最大应力分别为655MPa和562MPa，可见，弹体最大应力在压力波作用下比单峰瞬态压力作用下增加约16.5%，这对制导炮弹的发射过程是不利的。

以上结论为制导炮弹强度设计及火炮弹、炮、药耦合设计提供理论基础，同时为内弹道与装药结构设计提供参考。