修理工单重休假排队系统的更换模型研究*
2022-08-01贾金泽
贾金泽
(河南工学院 管理学院,河南 新乡 453003)
0 引言
目前,在管理学和工业工程领域,可修排队系统已成为学者们重点研究的方向之一。早期研究可修排队系统的文献大多都是假定服务台是“修复如新”的,但在工作实际中,服务台往往会因为发生故障而需要修理,不能为顾客提供服务,因此,对这类可修的排队系统的更换策略进行研究是非常有价值的。曹晋华和程侃[1]对服务台“修复如新”M/G/1排队系统的相关可靠性指标进行了研究,钟福金[2]等研究了设备可修且不能“修复如新”的可修排队系统的最优更换模型,贾积身等[3-5]又利用几何过程模型对服务台“修复非新”的M/G/1排队系统的更换策略进行了研究。唐应辉等[6]提出了“修理工单重休假”的概念,贾积身等[7-9]对此类系统的维修更换策略进行了研究,王敏、唐蓓蕾等[10-11]又进一步研究了单重休假的M/G/1排队系统的优化策略。
本文主要研究修理工单重休假的退化可修排队系统,并针对服务台“修复非新”和修理工休假时间为随机变量的情形,以被服务的顾客数N为更换策略,利用几何过程和概率论知识求出系统经长期运行单位时间内的期望效益的明显表达式。
1 模型假设
在文献[3]的相应假设下,再对模型做出如下假设:
设Zn为修理工第n个周期中的休假时间,{Zn,n=1,2,…}形成一个随机递减的几何过程,它的分布函数为H(dn-1t),其中d>1,t≥0,且设E(Z1)=γ;Xn,Yn,Zn,Wn,n=1,2,…相互独立;服务台一次更换费用为C,服务台在待修期间期望损失为C2(包括系统损失和顾客的等待损失),修理工在休假期间期望效益为C1。
2 期望效益
设Tn为服务台第n-1次与第n次更换之间的时间间隔(n=1,2,3,…),P(N)为系统在策略N下经长期运行单位时间内的期望效益。依照更新报酬定理可以得到
(1)
设K为服务台在连续N个顾客服务期内的故障次数,则它是一个随机变量,K=0,1,2,…。
由于
所以有


并且K的数学期望为


(3)
依照模型假定,系统的一个可能进程如图1。

图1 系统的一个可能进程
由系统进程以及假设,不难得到更新周期长为


为了推导E(L1),首先介绍下面的定理:
定理1 如果X,Y是两个非负独立的随机变量,它们的分布函数分别为F(x)和G(x),则有
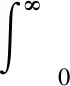
证明因为X,Y是两个独立的随机变量,所以

所以
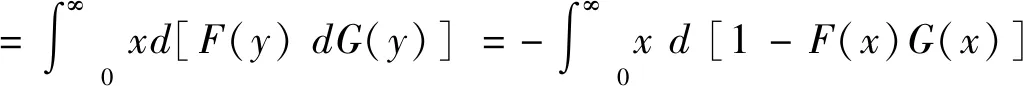

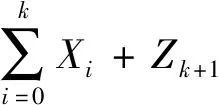
Qk(t)=Fk(t)*H(dkt)
根据条件期望性质、定理1以及(2)式,得
同理可得
由于
这里“[ ]′”表示求导运算。
所以

(4)
所以,平均更新周期长为
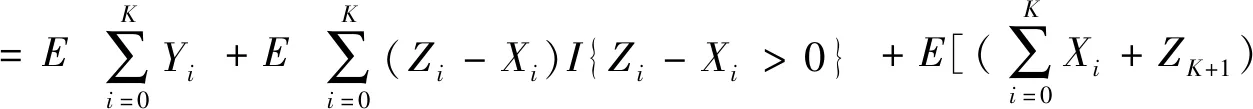
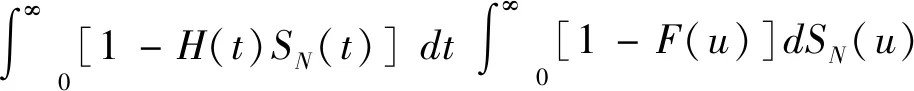
(5)
依据模型假设和系统进程,可得系统在一个更新周期内的期望效益为


(6)
由(1)(5)(6)三式,得到在策略N下系统经长期运行单位时间内的期望效益为
(7)
3 讨论
(1)若修理工为定期休假,且定期休假时间长度为T,则(7)式变为
(2)若服务台不会失效且不考虑修理工休假,这时(7)(11)两式均变为
显然,这样的系统就不需进行更换。
(3)若服务台能够“修复如新”且不考虑修理工休假,则a=b=1,(7)(11)两式均变为
其中
Fk(t)=F(t)*F(t)*F(t)*…*F(t)
SN(t)=S(t)*S(t)*S(t)*…*S(t)
(4)若服务台“修复非新”且不考虑修理工休假,则系统变为文献[3]中的系统。
4 结语
复杂系统的最优维修特性控制是保证系统可用度的重要手段,本文把可靠性模型中修理工单重休假的机制引入可修排队研究中,提出了一类新的退化可修排队系统维修更换模型,比以往所讨论的排队系统更具一般性,也更加符合实际;而且本文还考虑了服务台发生故障后的“修复不非新”。因此,本文进行的研究具有理论意义和工程应用价值,也具有前沿性。
