Kinetic theory of Jeans’gravitational instability in millicharged dark matter system
2022-08-01HuiChen陈辉WeiHengYang杨伟恒YuZhenXiong熊玉珍andSanQiuLiu刘三秋
Hui Chen(陈辉), Wei-Heng Yang(杨伟恒), Yu-Zhen Xiong(熊玉珍), and San-Qiu Liu(刘三秋)
Jiangxi Province Key Laboratory of Fusion and Information Control,Department of Physics,
Nanchang University,Nanchang 330031,China
Keywords: self-gravitating systems,millicharged dark matter,Jeans instability
1. Introduction
An open question, worthy of in-depth study, is whether the evolution and dynamics of interstellar gas clouds are strongly influenced by the unknown non-baryonic particles,or so called the dark matter (DM) with a total mass about five times of all the baryons.[1,2]Note that many observations and indirect experiments have confirmed the existence of DM in our universe,including the cosmic microwave background radiation,galaxy rotation curves,gravitational lensing and cluster observations,etc.[2–5]The Jeans instability,proposed firstly by Jeans,[6]describes the criteria for gravitational collapse and evolution of a self-gravitating system in linear regime,and has been extensively studied.[7–10]So, to examine DM’s role on the evolution of interstellar gas clouds,most of works have restudied the Jeans instability of self-gravitational systems in the background of DM.[11–14]For example,it has been proposed[11]that the Jeans mass and length of interstellar gas clouds will be modified by DM. Based on the framework of kinetic theory,Kremeret al.[12,13]have studied the Jeans instability of self-gravitational systems in the background of cold DM and indicated that the perturbation of baryons will catch up the DM perturbation at later period of structure formation.
The particle DM that obtains a small electric charge|qd|from the standard model photon is always called as mDM.In the past, many works have only focused mainly on the traditionally favored classes of DM candidates having only shortrange interactions with baryons, such as the weakly interacting massive particles (WIMPs), sterile neutrino or axion. An important focus is that whether DM has any non-gravitational interactions with the standard model particles,but a vast array of observations[4,15,16]have come to grief over lack of conclusive evidence before the appearance of mDM.The cosmic 21-cm absorption signal obtained by the experiment to detect the global epoch of reionization signature (EDGES)[17]is an informative and powerful evidence to prove the possibility of mDM, which motivates researchers interest on the exploration of DM with fractional charge.[18–20]This observations by the EDGES collaboration showed a stronger absorption spectrum than the maximum predicted value of standard cosmological model at a confidence level of 3.8 standard deviations.[17]To explain this discrepancy, Mu˜nozet al. have recently proposed the mDM could cool the baryons in the early universe via mDM-baryon scattering.[18]Based on his work, Liet al. have further found signal of mDM in supernova remnants and proposed the interaction between mDMs with the interstellar medium and electromagnetic fields within galaxies.[21]If confirmed,mDM would has unique phenomenological consequences due to its long-range electromagnetic interactions with the baryons and background magnetic field,which are easily occurred in astrophysical environments. In fact, the concept of charged dark matter has early been proposed by R´ujula in Ref. [22], that is, a stable particle having a unit charged and high mass can be viewed as a collisionless dark matter. Subsequent experiments[23]using both terrestrial and satellite data failed in the exploration,which shakes researchers faith in the possibility of charged dark matter. Recently, Chuzhoyet al. indicated that the reason why the existence of charged massive particles(CHAMPs)can not be detected is that CHAMPs having the charge and mass in the range of 100(qd/e)2≤md≤108(qd/e) TeV will interact with galactic magnetic fields, so they will evacuate from the galactic disk.[24]And they also further showed that the presence of CHAMPs is a reasonable way to solve several long-standing astrophysical problems, such as the underabundance of dwarf galaxies,[25]the cores of the dwarf galaxies with the too shallow density profiles[26]or other questions. Subsequently, the direct detection experiments of sub-GeV DM further prove that mDM obtains a sizeable scattering rates via DM–electron scattering.[27]The fraction,mass or charge of mDM are severely constrained by relevant observational phenomena and experimental results, such as the big bang nucleosynthesis(BBN),[28,29]stellar cooling,[30]SN1987A[31]and accelerator experiments.[32]In order to satisfy the constraint requirement for explaining the EDGES measurement,[18]while remaining consistent with the existing findings,[33–35]we have limited mDM to a viable range,with the fraction (md/MeV)0.0115%≤ fdm≤0.4%, mass 0.1 MeV≤md≤10 MeV, and charge 10-6e ≤qd≤10-4e,wherefdm=nmd0/nd0.
In light of the current understanding of generation mechanisms of mDM,kinetic mixing between a nearly massless dark photon and the standard model photon is the major mechanism to induce an effective electric charge for DM.[36]Some works have been reported that because of the tiny charges, mDM generally exists in supernova remnants in the form of a dark plasma instead of bound states.[21]Implicit in this scenario is the possibility that the interactions of dark plasma with interstellar medium gas may effectively influence the process of star formation. If, on the other hand, a supernova explosion happen around the nearby interstellar gas clouds, the strong shock waves generated by supernova explosion will sweep up the ambient interstellar medium and impact on the nearby interstellar gas clouds.[37,38]It can provide essential matters and energy for collapse of dense cloud core and then a new star is born. Similarly, mDM diffused in interstellar medium is also swept by the shock waves. Consideration of the existence of mDM around the interstellar gas clouds sheds light on one key question: whether the shocked mDM particles influences the process of a new star formation due to its electrostatic interaction. It is, thus, significant to study the role of charged dark matter in the evolution of interstellar gas clouds,as it may be a key to reveal the process of structure formation.
The rest of this paper is organized as follows: the derivation of the modified dispersion relation is shown in Section 2.In Section 3, we present the numerical results for the growth rate of Jeans instability. Conclusion and discussion are stated in Section 4.
2. Analysis of self-gravitational system with millicharged dark matter
Along the standard lines of kinetic theory, the dynamic behavior of self-gravitating system can be described by the collisionless Boltzmann equation which can be written in following way:
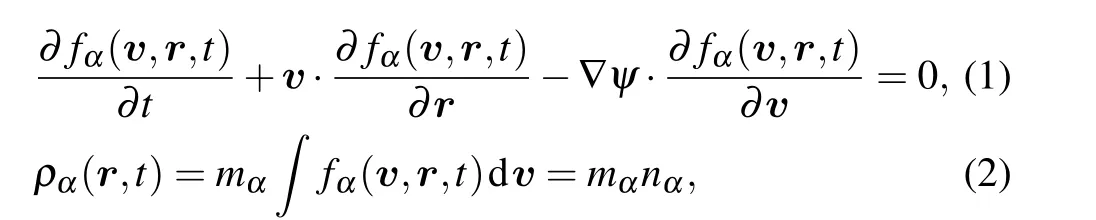
wherefα(v,r,t),ρα(r,t) andmαare the distribution function, density and mass ofαparticle, respectively. The subscriptα=b,d denotes two key ingredients, baryons matter(BM)and DM,respectively. Category of BM in our work usually indicates the matter composed by standard model particles,such as interstellar gas clouds.The gravitational potentialψis governed by Poisson equation

whereGthe gravitational constant. Consideration of the presence of mDM will result in a long-range electromagnetic interactions between DMs,which allows Eq.(1)to be re-written as

where electrostatic potentialφinduced by mDMs can be calculated by following equation:

For an infinite self-gravitational collisionless system with small perturbations, we assume equilibrium state is homogeneous and time-independent (i.e.,fα0(v,r,t) =fα0(v)), so particle distribution functions, gravitational and electrostatic potentials can be expanded as
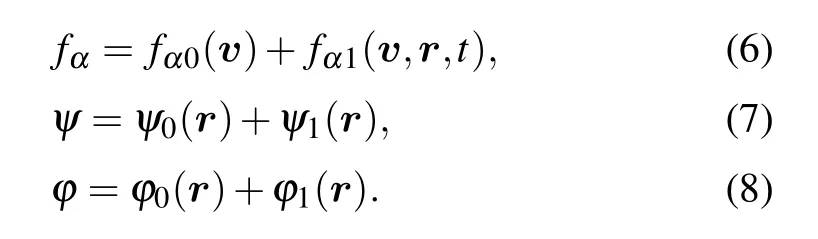
The equilibrium distribution of the self-gravitational system is described by the zero order termfα0(v), while the term of perturbation is showed by the first order correctionfα1(v,r,t)(≪fα0(v)). In addition, the unperturbed gravitational potential at equilibrium state and its first order correction are indicated byψ0(r) andψ1(r), respectively. Invoking Jeans swindle,[40]the unperturbed gravitational potentialψ0(r) can be regarded as a locally constant in system, so we have ∇ψ0(r)=0. Combining Eqs. (2)–(8) and making the fourier analyzing with plane wave ansatz, i.e.,X1∝exp[-i(ωt-k·r)](X=f,φ), whereωandkare the frequency and wavenumber of the perturbations, one obtains the dispersion relation


3. Instability analysis of self-gravitational system

which is the modified dispersion relation for Jeans modes involving mDM.Combining the integral formula(see Ref.[42],Eq.(3.466))
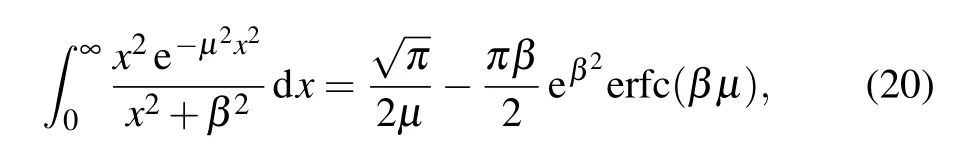
we have
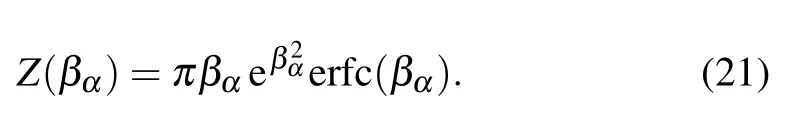
By substituting Eq.(21)into Eq.(19)and only considering the presence of interstellar gas cloud,Eq.(19)can be rewritten as
which is the classical dispersion relation for stellar systems firstly proposed by Binneyet al.[40]In addition, one can see that Eq.(19)predictably recovers to the neutral DM model[12]if we ignore the effect of mDM,

which further proves the rationality of Eq.(19).
Then, let us now discuss in more detail the unstable modes.It can be found that from Eq.(19)the solution depends onσbandσdas well asqd/md. It has been reported that in a typical type Ia supernova remnants,[21]the velocity of shockvshbegins to slow down tovsh~200 km/s and the shocked particles obtain kinetic energy via interaction with the ejecta.In this frame,the internal thermal speed of mDM particles approximate to the Milky way virial speed,σd≈220 km/s,[43]and we have assumed here that BM have thermal speed~0.69vsh,that is,σb≈138 km/s.[21]Based on the strict constraint of mDM mass and charge, here we adopt the upper value of mDM charge-to-mass ratioqd/md≈10-3e/MeV,as previously mentioned. The numerical results of Eq. (19)are shown in Fig. 1. Here, we plot the normalized frequencyω2*vs. normalized wave-numberk2*for different parameterfdm(≡nmd0/nd0).The black curve indicates the dispersion relation for the self-gravitational systems with BM alone,while other lines denote the dispersion relation curves with differentfdmand fixed value ofqd/md. It should be pointed out that the black curve corresponds to the classical result of stellar systems, which is identical to the black line in Fig. 5-1 of Ref. [40]. The dashed-blue curve corresponds to the dispersion relation for self-gravitational systems composed by BM and neutral DM. As can be seen, with the existence of neutral DM, the self-gravitational systems is more unstable even for wave-numbers of the perturbation greater than the classical critical Jeans number (kJb). In other words, the interaction between the BM and neutral DM allows the selfgravitational systems to become more unstable than the one only composed by BM,and therefore,structures are more easily formed in self-gravitational systems dominated by DM.This phenomenon occurs because DM is more easily to agglomerate comparing to the BM and then gravitational field generated from this initial agglomerate will rapidly attracts those BM to form a preliminary structure.[11]In addition,endowing the DM with a small fractional ‘mini-charge’ modifies the dispersion relation of self-gravitational systems, i.e.,with the increasing of the parameterfdm, the dispersion relation constantly rise along theω2*-axis,which means that selfgravitational systems will become more and more stable accompanying the increasing of mDM particles,in other words,mDM plays a significant role on the process of star formation.Physically, it can be viewed as the result of competition between the electromagnetic interaction and gravitational interaction: the electrostatic force generated by mDM oscillation resists gravitational force to inhibit formation of the initial agglomerate,and therefore,the structure formation will become more difficult in the presence of mDM.
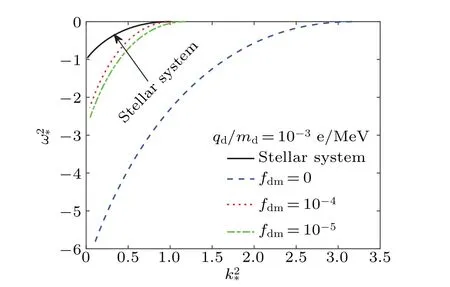
Fig.1. The normalized frequency ω2* =γ2/4πGρb0 versus the normalized wave number k2* =k2/k2Jb for different values of fdm parameter,where the black curve corresponds to the classical dispersion relation line in the interstellar systems.
4. Discussion and conclusion


Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 11763006 and 11863004), the fund from the Jiangxi Provincial Key Laboratory of Fusion and Information Control (Grant No. 20171BCD40005), and the Project of Scientific and Technological Innovation Base of Jiangxi Province,China(Grant No.20203CCD46008).
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Solutions of novel soliton molecules and their interactions of(2+1)-dimensional potential Boiti–Leon–Manna–Pempinelli equation
- Charge density wave states in phase-engineered monolayer VTe2
- High-pressure study of topological semimetals XCd2Sb2(X =Eu and Yb)
- Direct visualization of structural defects in 2D semiconductors
- Switchable down-,up-and dual-chirped microwave waveform generation with improved time–bandwidth product based on polarization modulation and phase encoding
- Machine learning potential aided structure search for low-lying candidates of Au clusters
